人教版数学八年级下册 18.1.1平行四边形的性质课件(42张ppt)
文档属性
| 名称 | 人教版数学八年级下册 18.1.1平行四边形的性质课件(42张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 19:46:30 | ||
图片预览







文档简介
(共42张PPT)
第十八章 平行四边形
第一节 平行四边形
18.1.1 平行四边形的性质
1.记住平行四边形的相关概念,探究平行四边形的性质。
2.会添加辅助线证明性质,记住性质并能应用性质解决简单的计算。
教学目标
重点: 1、探索并证明平行四边形的性质。
2、应用平行四边形的性质进行简单计算、推理。
难点: 正确利用平行四边形的性质解决问题。
重点难点
寻找生活中的平行四边形
导入新课
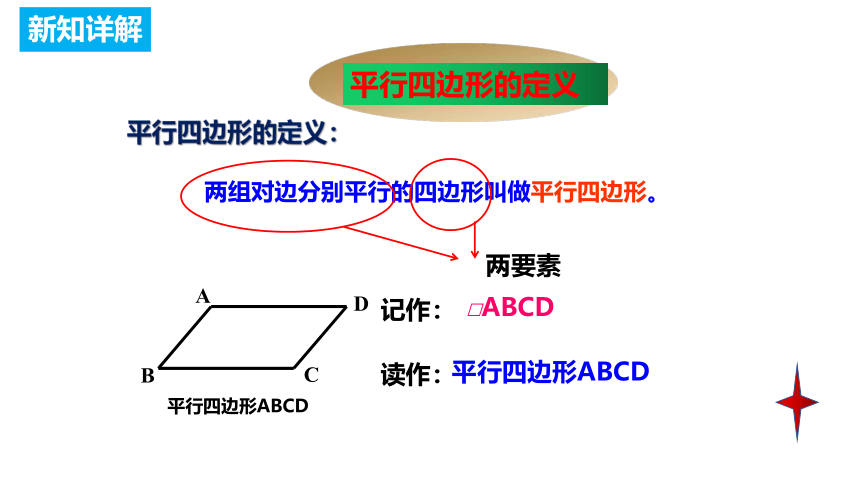
平行四边形的定义
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形。
平行四边形ABCD
平行四边形ABCD
□ABCD
记作:
读作:
A
D
C
B
两要素
新知详解
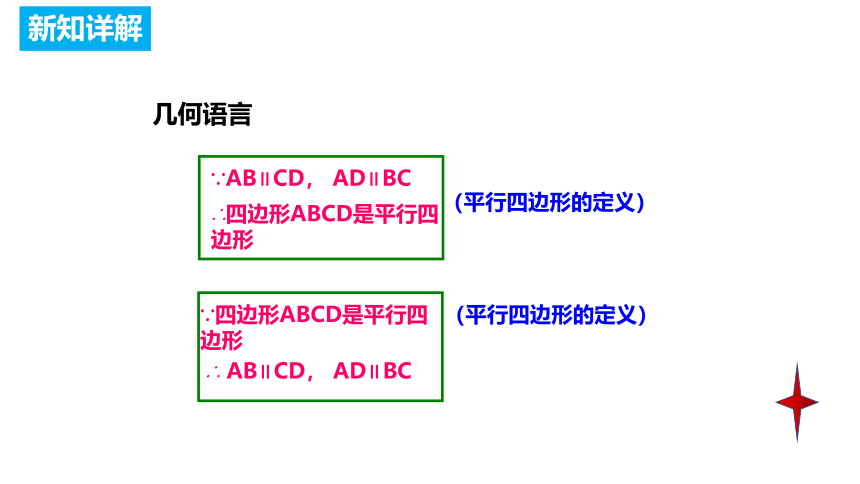
∵AB∥CD, AD∥BC
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
∴ AB∥CD, AD∥BC
(平行四边形的定义)
(平行四边形的定义)
几何语言
新知详解
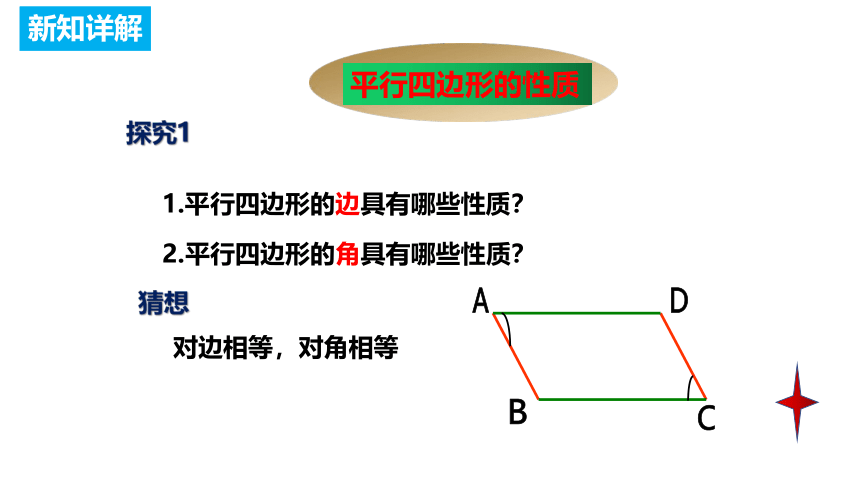
1.平行四边形的边具有哪些性质?
2.平行四边形的角具有哪些性质?
A
B
C
D
平行四边形的性质
探究1
猜想
对边相等,对角相等
新知详解
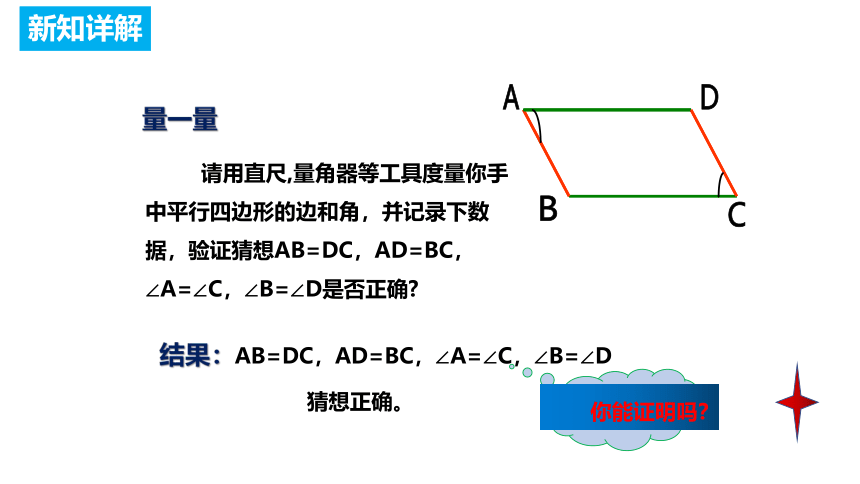
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
量一量
A
B
C
D
结果:AB=DC,AD=BC,∠A=∠C,∠B=∠D
猜想正确。
你能证明吗?
新知详解
从拼图可以得到什么启示?
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
新知详解
求证:AB=CD,AD=BC, ∠A=∠C, ∠B=∠D.
已知:四边形ABCD为平行四边形
证明:
∵四边形ABCD为平行四边形
∴AD∥BC,AB ∥CD
∴ ∠1=∠2, ∠3=∠4
在△ADC与△CBA中
∠1=∠2,
AC=CA
∠3=∠4
∴ △ADC≌△CBA
∴ AD=CB,AB=CD, ∠B=∠D
又∵∠1+∠4=∠2+∠3
∴∠BAD=∠DCB
连结AC
A
B
C
D
4
1
3
2
新知详解
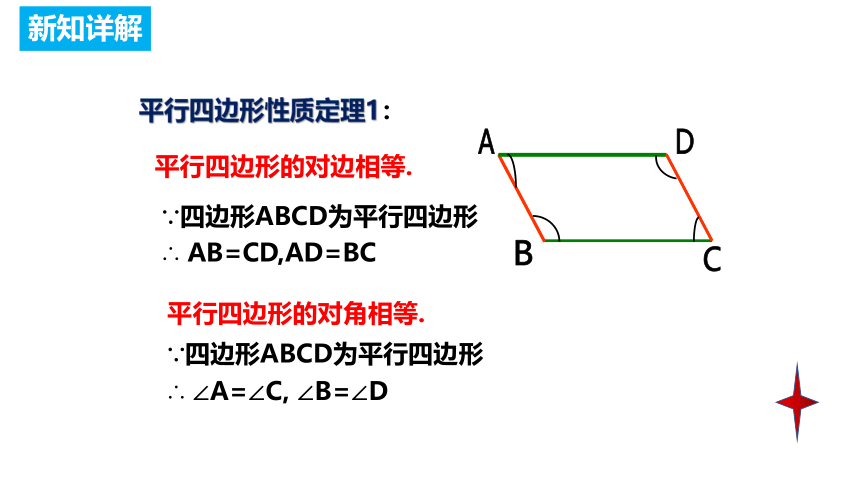
平行四边形性质定理1:
平行四边形的对边相等.
∵四边形ABCD为平行四边形
∴ AB=CD,AD=BC
平行四边形的对角相等.
∵四边形ABCD为平行四边形
∴ ∠A=∠C, ∠B=∠D
A
B
C
D
新知详解
平行四边形中知道一个角就可以求出另外三个角的度数。
想一想
已知平行四边形一个内角的度数,你能确定其他内角的度数吗?
A
B
C
D
56°
56°
124°
124°
新知详解
例1 如图, □ ABCD中,DE⊥AB,BF⊥CD,
垂足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
证明:
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
∵DE⊥AB,BF⊥CD,
∴∠AED=∠CFB=90°
∴△AED≌△CFB.
∴AE=CF.
新知详解
H
A
D
G
若a // b,作 DA // HG ,分别交 b于D、H,交 a于A、G。则线段DA与HG有什么关系?
由平行四边形的对边性质可知:DA=HG
两条平行线之间的平行线段相等.
b
a
两条平行线之间的距离:
又作 CB // HG ,交 b于C,交 a于B。则线段CB与HG有什么关系?
CB=HG=DA
C
B
新知详解
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
则 DA HG CB.
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
A
B
C
D
a
b
H
G
=
=
两条平行线之间的距离相等。
新知详解
已知一点到两条平行线的距离分别是1cm,4cm,则这两条平行线之间距离是 cm。
分析:当如图1所示时,
两平行线间的距离=4﹣1=3cm;
当如图2所示时,
两平行线间的距离=4+1=5cm.
故答案为:3或5。
3或5
巩固练习
1.在平行四边形ABCD中,∠A+∠C=140°,那么∠A= ,∠D= .
分析:由四边形ABCD是平行四边形,根据平行四边形的对角相等,即可得∠A=∠C,∠B=∠D,又由∠A+∠C=140°,∠A+∠B+∠C+∠D=360°,即可求得答案.
110°
70°
精题突破
2.如图,在 ABCD中,E,F分别是DC,BA延长线上的点,且AE∥CF,AE,CF分别交BC,AD于点G,H,求证:EG=FH.
分析:由四边形ABCD是平行四边形,可得AB∥CD,AD∥BC,又由AE∥CF,即可证得四边形AECF与四边形AGCH是平行四边形,继而可证得HF=GE.
精题突破
解析:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AE∥CF,
∴四边形AECF与四边形AGCH是平行四边形,
∴AE=CF,AG=CH,
∴AG-AE=CH-CF,
∴EG=FH.
精题突破
3.平行四边形的两邻边的比是2:5,周长为28cm,求平行四边形的各边的长.
分析:根据平行四边形的性质可知:邻边之和为周长的一半,可设较短的边为2x,则较长的为5x,根据题意列方程即可求出.
精题突破
解析:根据平行四边形的性质可知:邻边之和为周长的一半,
设较短的边为2x,则较长的为5x,
∴2x+5x=14,
∴x=2,
∴5x=5×2=10,2x=2×2=4,
∴平行四边形的各边的长分别为10cm、4cm、10cm、4cm.
精题突破
新课讲解
如图,在□ ABCD中,连接AC,BD,并设它们相交
于点O.OA与OC,OB与OD有什么关系?
D
A
B
C
O
平行四边形的对角线互相平分。
探究2
猜想
新知详解
●
A
D
O
C
B
D
B
O
C
A
把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么
旋转180°后与自身重合平行四边形 ABCD是中心对称图形,点O是对称中心
新知详解
证明:∵四边形ABCD是平行四边形,
已知:如图,在口ABCD中,对角线AC,BD交于点O.求证:OA=OC,OB=OD.
A
C
D
B
O
在△AOB和△COD中
∴AB∥CD,AD ∥BC(平行四边形的性质)
∴ ∠1=∠2, ∠3=∠4(两直线平行,内错角相等)
∴ △AOB≌△COD(ASA )
∴OA=OC,OB=OD.(全等三角形的对应边相等)
1
2
3
4
新知详解
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
平行四边形性质定理2:
新知详解
例2 如图,在口ABCD中,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及口ABCD的面积.
A
O
C
B
D
解:∵ 四边形ABCD是平行四边形,
∴BC=AD=8, CD=AB=10.
∵ AC⊥BC,
∴ΔABC是直角三角形.
∴AC==6
又 OA=OC
∴ OA=AC=3,∴S口ABCD=BC·AC=8×6=48
新知详解
4.如图,在 ABCD中,对角线AC与BD相交于点O,BD=2AB,E是OA的中点.求证:BE⊥AC.
分析:由平行四边形的性质得出BD=2OB,再证明OB=AB,由E为OA的中点,根据三线合一性质即可证出BE⊥AC.
精题突破
解:∵四边形ABCD是平行四边形,
∴BD=2OB,
∵BD=2AB,
∴OB=AB,
又∵E为OA的中点,
∴BE⊥AC.
精题突破
分析:根据AC=AB证明= ,从而可证得△AOB∽△ABC,得对应角相等,同时再利用平行线所截的内错角相等得出结论.
5、如图,平行四边形ABCD中,AC=AB,求证:∠ABD=∠DAC.
精题突破
解析:∵四边形ABCD是平行四边形,
∴AC=2AO,AD∥BC,
∵AC=AB,
∴AO=AB,∴ =,
∵==,∴= ,
∵∠CAB=∠CAB,
∴△AOB∽△ABC,∴∠ABD=∠ACB,
∵AD∥BC,∴∠ACB=∠DAC,∴∠ABD=∠DAC
利用平行线所截的内错角相等。
精题突破
1、如图,在 ABCD中,CE⊥AB,E为垂足,如果∠BCE=35°,则∠D的度数为( )
A.55° B.35°
C.25° D.30°
A
达标检测
2、在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.2:2:1:1 D.2:1:2:1
D
达标检测
3、如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
A.6 B.8
C.14 D.16.
C
达标检测
4.如图,在 ABCD中,AE是∠BAD的平分线交DC于点E,求证:CE+BC=AB。
分析:根据平行四边形的性质,可以得到AB=CD,AD=BC,由AE是∠BAD的平分线,灵活变化即可得到CE、BC、AB的关系,本题得以解决.
达标检测
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AB∥CD,
∴∠DEA=∠EAB,
∵AE是∠BAD的平分线,
∴∠DAE=∠EAB,∴∠DAE=∠DEA,
∴DE=AD,
∴DC=AD+CE,
∴AB=CE+BC,
即CE+BC=AB.
达标检测
1、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形
2、平行四边形的性质:
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
课堂小结
1.已知如图,E、F为 ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF。(用两种方法证明)
分析:①由平行四边形的性质得出AB=CD,∠BAC=∠DCA,由SAS证明△ABE≌△CDF,得出对应边相等即可;
②连接DE、BF,连接BD交AC于O,由平行四边形的性质得出OA=OC,OB=OD,证出OE=OF,得出四边形BFDE是平行四边形,即可得出结论。
拓展提升
解析:方法①:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
∴∠BAC=∠DCA.∴∠BAE=∠DCF,
在△ABE和△CDF中,
AE=CF
∠BAE=∠DCF
AB=CD ,
∴△ABE≌△CDF(SAS),∴BE=DF。
拓展提升
解析:方法②:连接DE、BF,连接BD交AC于O,
如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴BE=DF.
拓展提升
2.求证:平行四边形两条对角线的平方和等于四条边的平方和。
分析:这是一个文字命题的证明题,先根据题意画出图形,写出已知、求证、证明过程。作AE⊥BC于点E,DF⊥BC交BC的延长线于F,再根据四边形ABCD是平行四边形,求证△ABE≌△DCF,得出AE=DF,BE=CF,由勾股定理得AC2=AE2+EC2=AE2+(BC-BE)2,
BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2
拓展提升
解析:如图:在平行四边形ABCD中,AC,BD是其两条对角线,
求证:AC2+BD2=AB2+BC2+CD2+AD2
证明:作AE⊥BC于点E,DF⊥BC交BC的延长线于F,
则∠AEB=∠DFC=90°.
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
∴∠ABE=∠DCF,
∴△ABE≌△DCF,
∴AE=DF,BE=CF。
拓展提升
在Rt△ACE和Rt△BDF中,由勾股定理,得
AC2=AE2+EC2=AE2+(BC-BE)2,
BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2,
∴AC2+BD2=2AE2+2BC2+2BE2=2(AE2+BE2)+2BC2.
又∵AE2+BE2=AB2,
即:AC2+BD2=2(AB2+BC2).
∵AB=CD,AD=BC,
∴AC2+BD2=AB2+BC2+CD2+AD2
拓展提升
第十八章 平行四边形
第一节 平行四边形
18.1.1 平行四边形的性质
1.记住平行四边形的相关概念,探究平行四边形的性质。
2.会添加辅助线证明性质,记住性质并能应用性质解决简单的计算。
教学目标
重点: 1、探索并证明平行四边形的性质。
2、应用平行四边形的性质进行简单计算、推理。
难点: 正确利用平行四边形的性质解决问题。
重点难点
寻找生活中的平行四边形
导入新课
平行四边形的定义
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形。
平行四边形ABCD
平行四边形ABCD
□ABCD
记作:
读作:
A
D
C
B
两要素
新知详解
∵AB∥CD, AD∥BC
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
∴ AB∥CD, AD∥BC
(平行四边形的定义)
(平行四边形的定义)
几何语言
新知详解
1.平行四边形的边具有哪些性质?
2.平行四边形的角具有哪些性质?
A
B
C
D
平行四边形的性质
探究1
猜想
对边相等,对角相等
新知详解
请用直尺,量角器等工具度量你手中平行四边形的边和角,并记录下数据,验证猜想AB=DC,AD=BC,∠A=∠C,∠B=∠D是否正确
量一量
A
B
C
D
结果:AB=DC,AD=BC,∠A=∠C,∠B=∠D
猜想正确。
你能证明吗?
新知详解
从拼图可以得到什么启示?
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。
用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?
新知详解
求证:AB=CD,AD=BC, ∠A=∠C, ∠B=∠D.
已知:四边形ABCD为平行四边形
证明:
∵四边形ABCD为平行四边形
∴AD∥BC,AB ∥CD
∴ ∠1=∠2, ∠3=∠4
在△ADC与△CBA中
∠1=∠2,
AC=CA
∠3=∠4
∴ △ADC≌△CBA
∴ AD=CB,AB=CD, ∠B=∠D
又∵∠1+∠4=∠2+∠3
∴∠BAD=∠DCB
连结AC
A
B
C
D
4
1
3
2
新知详解
平行四边形性质定理1:
平行四边形的对边相等.
∵四边形ABCD为平行四边形
∴ AB=CD,AD=BC
平行四边形的对角相等.
∵四边形ABCD为平行四边形
∴ ∠A=∠C, ∠B=∠D
A
B
C
D
新知详解
平行四边形中知道一个角就可以求出另外三个角的度数。
想一想
已知平行四边形一个内角的度数,你能确定其他内角的度数吗?
A
B
C
D
56°
56°
124°
124°
新知详解
例1 如图, □ ABCD中,DE⊥AB,BF⊥CD,
垂足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
证明:
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=CB.
∵DE⊥AB,BF⊥CD,
∴∠AED=∠CFB=90°
∴△AED≌△CFB.
∴AE=CF.
新知详解
H
A
D
G
若a // b,作 DA // HG ,分别交 b于D、H,交 a于A、G。则线段DA与HG有什么关系?
由平行四边形的对边性质可知:DA=HG
两条平行线之间的平行线段相等.
b
a
两条平行线之间的距离:
又作 CB // HG ,交 b于C,交 a于B。则线段CB与HG有什么关系?
CB=HG=DA
C
B
新知详解
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
则 DA HG CB.
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
A
B
C
D
a
b
H
G
=
=
两条平行线之间的距离相等。
新知详解
已知一点到两条平行线的距离分别是1cm,4cm,则这两条平行线之间距离是 cm。
分析:当如图1所示时,
两平行线间的距离=4﹣1=3cm;
当如图2所示时,
两平行线间的距离=4+1=5cm.
故答案为:3或5。
3或5
巩固练习
1.在平行四边形ABCD中,∠A+∠C=140°,那么∠A= ,∠D= .
分析:由四边形ABCD是平行四边形,根据平行四边形的对角相等,即可得∠A=∠C,∠B=∠D,又由∠A+∠C=140°,∠A+∠B+∠C+∠D=360°,即可求得答案.
110°
70°
精题突破
2.如图,在 ABCD中,E,F分别是DC,BA延长线上的点,且AE∥CF,AE,CF分别交BC,AD于点G,H,求证:EG=FH.
分析:由四边形ABCD是平行四边形,可得AB∥CD,AD∥BC,又由AE∥CF,即可证得四边形AECF与四边形AGCH是平行四边形,继而可证得HF=GE.
精题突破
解析:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∵AE∥CF,
∴四边形AECF与四边形AGCH是平行四边形,
∴AE=CF,AG=CH,
∴AG-AE=CH-CF,
∴EG=FH.
精题突破
3.平行四边形的两邻边的比是2:5,周长为28cm,求平行四边形的各边的长.
分析:根据平行四边形的性质可知:邻边之和为周长的一半,可设较短的边为2x,则较长的为5x,根据题意列方程即可求出.
精题突破
解析:根据平行四边形的性质可知:邻边之和为周长的一半,
设较短的边为2x,则较长的为5x,
∴2x+5x=14,
∴x=2,
∴5x=5×2=10,2x=2×2=4,
∴平行四边形的各边的长分别为10cm、4cm、10cm、4cm.
精题突破
新课讲解
如图,在□ ABCD中,连接AC,BD,并设它们相交
于点O.OA与OC,OB与OD有什么关系?
D
A
B
C
O
平行四边形的对角线互相平分。
探究2
猜想
新知详解
●
A
D
O
C
B
D
B
O
C
A
把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么
旋转180°后与自身重合平行四边形 ABCD是中心对称图形,点O是对称中心
新知详解
证明:∵四边形ABCD是平行四边形,
已知:如图,在口ABCD中,对角线AC,BD交于点O.求证:OA=OC,OB=OD.
A
C
D
B
O
在△AOB和△COD中
∴AB∥CD,AD ∥BC(平行四边形的性质)
∴ ∠1=∠2, ∠3=∠4(两直线平行,内错角相等)
∴ △AOB≌△COD(ASA )
∴OA=OC,OB=OD.(全等三角形的对应边相等)
1
2
3
4
新知详解
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
平行四边形性质定理2:
新知详解
例2 如图,在口ABCD中,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及口ABCD的面积.
A
O
C
B
D
解:∵ 四边形ABCD是平行四边形,
∴BC=AD=8, CD=AB=10.
∵ AC⊥BC,
∴ΔABC是直角三角形.
∴AC==6
又 OA=OC
∴ OA=AC=3,∴S口ABCD=BC·AC=8×6=48
新知详解
4.如图,在 ABCD中,对角线AC与BD相交于点O,BD=2AB,E是OA的中点.求证:BE⊥AC.
分析:由平行四边形的性质得出BD=2OB,再证明OB=AB,由E为OA的中点,根据三线合一性质即可证出BE⊥AC.
精题突破
解:∵四边形ABCD是平行四边形,
∴BD=2OB,
∵BD=2AB,
∴OB=AB,
又∵E为OA的中点,
∴BE⊥AC.
精题突破
分析:根据AC=AB证明= ,从而可证得△AOB∽△ABC,得对应角相等,同时再利用平行线所截的内错角相等得出结论.
5、如图,平行四边形ABCD中,AC=AB,求证:∠ABD=∠DAC.
精题突破
解析:∵四边形ABCD是平行四边形,
∴AC=2AO,AD∥BC,
∵AC=AB,
∴AO=AB,∴ =,
∵==,∴= ,
∵∠CAB=∠CAB,
∴△AOB∽△ABC,∴∠ABD=∠ACB,
∵AD∥BC,∴∠ACB=∠DAC,∴∠ABD=∠DAC
利用平行线所截的内错角相等。
精题突破
1、如图,在 ABCD中,CE⊥AB,E为垂足,如果∠BCE=35°,则∠D的度数为( )
A.55° B.35°
C.25° D.30°
A
达标检测
2、在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.2:2:1:1 D.2:1:2:1
D
达标检测
3、如图,平行四边形ABCD中,AB=6,BC=8,AC的垂直平分线交AD于E,则三角形CDE的周长是( )
A.6 B.8
C.14 D.16.
C
达标检测
4.如图,在 ABCD中,AE是∠BAD的平分线交DC于点E,求证:CE+BC=AB。
分析:根据平行四边形的性质,可以得到AB=CD,AD=BC,由AE是∠BAD的平分线,灵活变化即可得到CE、BC、AB的关系,本题得以解决.
达标检测
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AB∥CD,
∴∠DEA=∠EAB,
∵AE是∠BAD的平分线,
∴∠DAE=∠EAB,∴∠DAE=∠DEA,
∴DE=AD,
∴DC=AD+CE,
∴AB=CE+BC,
即CE+BC=AB.
达标检测
1、平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形
2、平行四边形的性质:
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
课堂小结
1.已知如图,E、F为 ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF。(用两种方法证明)
分析:①由平行四边形的性质得出AB=CD,∠BAC=∠DCA,由SAS证明△ABE≌△CDF,得出对应边相等即可;
②连接DE、BF,连接BD交AC于O,由平行四边形的性质得出OA=OC,OB=OD,证出OE=OF,得出四边形BFDE是平行四边形,即可得出结论。
拓展提升
解析:方法①:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
∴∠BAC=∠DCA.∴∠BAE=∠DCF,
在△ABE和△CDF中,
AE=CF
∠BAE=∠DCF
AB=CD ,
∴△ABE≌△CDF(SAS),∴BE=DF。
拓展提升
解析:方法②:连接DE、BF,连接BD交AC于O,
如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴BE=DF.
拓展提升
2.求证:平行四边形两条对角线的平方和等于四条边的平方和。
分析:这是一个文字命题的证明题,先根据题意画出图形,写出已知、求证、证明过程。作AE⊥BC于点E,DF⊥BC交BC的延长线于F,再根据四边形ABCD是平行四边形,求证△ABE≌△DCF,得出AE=DF,BE=CF,由勾股定理得AC2=AE2+EC2=AE2+(BC-BE)2,
BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2
拓展提升
解析:如图:在平行四边形ABCD中,AC,BD是其两条对角线,
求证:AC2+BD2=AB2+BC2+CD2+AD2
证明:作AE⊥BC于点E,DF⊥BC交BC的延长线于F,
则∠AEB=∠DFC=90°.
∵四边形ABCD是平行四边形,
∴AB=DC,AB∥CD,
∴∠ABE=∠DCF,
∴△ABE≌△DCF,
∴AE=DF,BE=CF。
拓展提升
在Rt△ACE和Rt△BDF中,由勾股定理,得
AC2=AE2+EC2=AE2+(BC-BE)2,
BD2=DF2+BF2=DF2+(BC+CF)2=AE2+(BC+BE)2,
∴AC2+BD2=2AE2+2BC2+2BE2=2(AE2+BE2)+2BC2.
又∵AE2+BE2=AB2,
即:AC2+BD2=2(AB2+BC2).
∵AB=CD,AD=BC,
∴AC2+BD2=AB2+BC2+CD2+AD2
拓展提升
