2022中考数学三轮冲刺专题突破01 规律探索型问题 课件(共48张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺专题突破01 规律探索型问题 课件(共48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 08:34:48 | ||
图片预览











文档简介
(共48张PPT)
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 01
规律探索型问题
一、常见的数列:
(1)正整数:1,2,3,4,5,…,第n项为n,前n项和为;
(2)奇数:1,3,5,7,…,第n项为2n-1,前n项和为n2;
(3)偶数:2,4,6,8,…,第n项为2n,前n项和为n(n+1);
(4)1,-1,1,-1,1,-1,…,第n项为(-1)n+1;-1,1,-1,1,-1,1,…,第n项为(-1)n;
(5)a,a+d,a+2d,a+3d,…,第n项为a+(n-1)d(特点:第一项为a,从第二项开始每一项比前一项增加d).
类型一
数式规律探索
二、解题策略
(1)分式型问题:分别观察分子、分母的特征及相邻项的变化规律;也可考虑先化异分母分式为同分母分式,再求解;
(2)乘积形式:分别表示,再相乘,如a,2a2,3a3,4a4,…,第n项可表示为nan;
(3)等式型问题:给等式标序号,分别用序号表示出等式的左右两边,代入序号验证.
1.[2021·云南]按一定规律排列的单项式:
a2,4a3,9a4,16a5,25a6,…,第n个单项式是 ( )
A.n2an+1 B.n2an-1
C.nnan+1 D.(n+1)2an
A
2.[2021·济宁]按规律排列的一组数据:,,□,,,…,其中□内应填的数是 ( )
A. B. C. D.
D
[解析]观察这组数据发现:分子为连续的奇数,分母为序号的平方+1,∴第n个数据为:.当n=3时,□的分子为5,分母=32+1=
10,∴这个数为.
3.[2021·甘肃省卷]一组按规律排列的代数式:a+2b,a2-2b3,
a3+2b5,a4-2b7,…,则第n个式子是 .
4.[2020·咸宁]按一定规律排列的一列数:3,32,3-1,33,3-4,37,3-11,
318,…,若a,b,c表示这列数中的连续三个数,猜想a,b,c满足的关系式是 .
an+(-1)n+1·2b2n-1
bc=a
[解析]一列数:3,32,3-1,33,3-4,37,3-11,318,…,可发现:第n个数等于前面两个数的商.∵a,b,c表示这列数中的连续三个数,∴bc=a,因此本题填bc=a.
5.[2020·张家界]观察下面的变化规律:=1-,,
,,…,
根据上面的规律计算:+…+= .
[解析]+…+=1-+…+
=1-.
6.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,若把第一个三角形数记为x1,第二个三角形数记为x2,…,第n个三角形数记为xn,则xn+xn+1= .
(n+1)2
[解析]∵x1+x2=1+3=4;x2+x3=3+6=9;x3+x4=6+10=16;
x4+x5=10+15=25;x5+x6=15+21=36;…;∴xn+xn+1=(n+1)2.
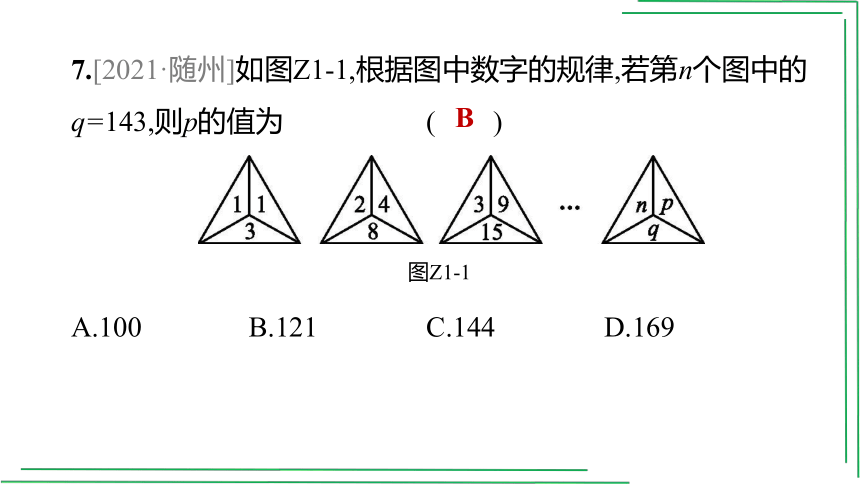
7.[2021·随州]如图Z1-1,根据图中数字的规律,若第n个图中的q=143,则p的值为 ( )
A.100 B.121 C.144 D.169
图Z1-1
B
[解析]通过观察可得规律:p=n2,q=(n+1)2-1,
∵q=143,
∴(n+1)2-1=143,解得n=11(负值已舍),
∴p=n2=112=121.
8.[2021·怀化]观察等式:2+22=23-2,2+22+23=24-2,2+22+23+24=
25-2,…,已知按一定规律排列的一组数:2100,2101,2102,…,2199,若2100=m,用含m的代数式表示这组数的和是 .
m2-m
[解析]由题意得2100+2101+2102+…+2199=(2+22+23+…+2199)-(2+22+23+…+299)=(2200-2)-(2100-2)=(2100)2-2100=m2-m.
9.[2021·恩施州]古希腊数学家定义了五边形数,如下表所示,将点按照表中方式排列成五边形点阵,图形中的点的个数即五边形数.
图形 …
五边 形数 1 5 12 22 35 51 …
将五边形数1,5,12,22,35,51,…,排成如图Z1-2所示的数图:
观察这个数图,则这个数图中的第八行从左至右第2个数为
.
图Z1-2
1335
[解析]观察表中图形及数字的变化规律可得第n个五边形数可表示为:1+2+3+…+(n-1)+n2,
由数图可知前七行数的个数和为:1+2+3+…+7=28,
∴数图中的第八行从左至右第2个数是第30个五边形数,
即n=30,∴把n=30代入得
1+2+3+…+29+302=1335.
解决图形规律题的步骤:①标序数——按图号标序号;
②找规律——数出每一项的元素个数,将其表示成与序数有关的式子,用n表示出来;
③验证——代入序号验证所归纳的式子是否正确.
类型二
图形规律探索
1.[2020·重庆A卷]把黑色三角形按如图Z1-3所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形……按此规律排列下去,则第⑤个图案中黑色三角形的个数为 ( )
A.10 B.15 C.18 D.21
图Z1-3
B
[解析]本题考查了图形规律的探索,观察图形可知,第①个图案中黑色三角形个数为1,第②个图案中黑色三角形个数为3=1+2,第③个图案中黑色三角形个数为6=1+2+3,…,按此规律可知第⑤个图案中黑色三角形个数为1+2+3+4+5=15.
2.[2021·玉林]观察下列树枝分杈的规律图,若第n个图树枝数用Yn表示,则Y9-Y4= ( )
A.15×24 B.31×24 C.33×24 D.63×24
图Z1-4
B
[解析]由第1个图可知Y1=1=21-1,由第2个图可知Y2=3=22-1,由第3个图可知Y3=7=23-1,由第4个图可知Y4=15=24-1,
可知Yn=2n-1.即Y9=29-1,Y4=24-1.
因此Y9-Y4=29-1-(24-1)=29-24=24×(25-1)=31×24.
3.用若干大小相同的黑白两种颜色的正方形瓷砖,按下列规律铺成一列图案,则第7个图案中黑色瓷砖的个数是 ( )
A.19 B.20 C.21 D.22
图Z1-5
D
4.[2020·德州]下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案黑色棋子的个数是 ( )
A.148 B.152 C.174 D.202
图Z1-6
C
[解析]图①中的黑色棋子数是0+2×(1+2+3);图②中的黑色棋子数是2+2×(1+2+3+4);
图③中的黑色棋子数是4+2×(1+2+3+4+5);图④中的黑色棋子数是6+2×(1+2+3+4+5+6);…,
第10个这样的图案黑色棋子数是2×9+2×(1+2+3+4+5+6+…+11+12)
=18+2××12×(1+12)=174.
5.[2021·凉山州]如图Z1-7,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍;拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍……照这样拼图,则第n个图形需要 根火柴棍.
图Z1-7
(2n+1)
[解析]第一个图形需要火柴棍:3=1×2+1;
第二个图形需要火柴棍:5=2×2+1;
第三个图形需要火柴棍:7=3×2+1;…;
∴第n个图形需要火柴棍:2n+1.
6.[2020·牡丹江]如图Z1-8是由同样大小的圆按一定规律排列所组成的,其中第1个图形中一共有4个圆,第2个图形中一共有8个圆,第3个图形中一共有14个圆,第4个图形中一共有22个圆……按此规律排列下去,第9个图形中圆的个数是 个.
图Z1-8
92
[解析]根据已有图形找规律,第1个图形中一共有1×(1+1)+2=4个圆,第2个图形中一共有2×(2+1)+2=8个圆,第3个图形中一共有3×(3+1)+2=14个圆,第4个图形中一共有4×(4+1)+2=22个圆,故可得第n个图形中圆的个数是n(n+1)+2,所以第9个图形中圆的个数是9×(9+1)+2=92.
7.如图Z1-9,Rt△ABC中有n个正方形从左往右依次排开(每个正方形右上角的顶点均在AB边上,下方的两个顶点均在BC边上),第一个正方形的边长DF=9 cm,第二个正方形的边长GK=6 cm,
则从左往右第n个正方形的边长= cm.
图Z1-9
9×()n-1
[解析]∵第一个正方形的边长DF=9 cm,第二个正方形的边长GK=6 cm,
∴EF=9,∴GF=EF-EG=9-6=3,设PQ=x,
∵GK∥PQ,∴∠FKG=∠KQP.
又∵∠FGK=∠KPQ=90°,
∴△FGK∽△KPQ,∴,∴,解得x=4.
∵第二个正方形的边长为9×=6,第三个正方形的边长为9×()2=4,
∴第n个正方形的边长为9×()n-1.
8.如图Z1-10①是一个三角形,分别连接这个三角形三边的中点,得到图②,再分别连接图②中的小三角形三边的中点,得到图③.按此继续下去,请你根据每个图形中的三角形个数的规律,完成下列问题.
图Z1-10
(1)将下表填写完整:
(2)在第n个图形中有 个三角形(用含n的式子表示);
(3)第 个图形中有2021个三角形.
图形编号 1 2 3 4 5 …
三角形个数 1 5 9 …
图Z1-10
13
17
4n-3
506
坐标系中的规律问题,多为循环变化性问题,关键是依次正确求出前几步的结论,寻找点的横、纵坐标的变化规律,或者横、纵坐标之间的关系,或者找到循环规律.
类型三
坐标系中的规律探索
1.[2021·临沂]实验证实,放射性物质放出射线后,质量将减少,减少的速度开始较快,后来较慢,物质所剩的质量与时间成某种函数关系.如图Z1-11为表示镭的放射规律的函数图象,据此可计算32 mg镭缩减为1 mg所用的
时间大约是 ( )
A.4860年 B.6480年
C.8100年 D.9720年
图Z1-11
C
[解析]有m0→m0,0→1620,
m0→m0,1620→3240,
m0→m0,3240→4860,
∴每经过1620年,镭的质量就缩小到原来的一半,
有32 mg镭缩减为16 mg用时1620年,
16 mg镭缩减为8 mg用时1620年,
8 mg镭缩减为4 mg用时1620年,
4 mg镭缩减为2 mg用时1620年,
2 mg镭缩减为1 mg用时1620年,
∴32 mg镭缩减为1 mg用时1620×5=8100(年).
2.如图Z1-12,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2021次得到正方形OA2021B2021C2021,那么点A2021的坐标是 ( )
A.(,-) B.(1,0)
C.(-,-) D.(0,-1)
图Z1-12
C
[解析]∵四边形OABC是正方形,且OA=1,∴A(0,1),
∵正方形OABC绕点O依次顺时针旋转45°,
∴A1(,),A2(1,0),A3(,-),A4(0,-1),
A5(-,-),…
发现是8次一循环,∴2021÷8=252……5,
∴点A2021的坐标为(-,-),故选C.
3.[2021·仙桃]如图Z1-13,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得点P1
(-1,-1);接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点P2;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点P3;接着水平向右平移4
个单位长度,再竖直向上平移4个单位长度
得到点P4……按此作法进行下去,则点P2021
的坐标为 .
图Z1-13
(-1011,-1011)
[解析]先根据点坐标的平移变换规律求出点P2(1,1),P3(-2,-2),
P4(2,2),P5(-3,-3),归纳类推得:点P2n-1(-n,-n),其中n为正整数,
∵2021=2×1011-1,∴点P2021(-1011,-1011).
4.[2021·河北承德一模]如图Z1-14,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记
△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3
于点B2,记△P2B2P3的面积为S3……依次
进行下去,则S3= ,最后记△Pn-1Bn-1Pn
(n>1)的面积为Sn,则Sn= .
图Z1-14
[解析]当x=1时,y=x2=,则P1(1,),所以S1=×1×;
当x=2时,y=x2=2,则P2(2,2),所以S2=×1×(2-)=;
当x=3时,y=x2=,则P3(3,),所以S3=×1×(-2)=;
同样方法可得S4=,所以Sn=.故答案为,.
5.[2021·达州]在平面直角坐标系中,等边三角形AOB如图Z1-15放置,点A的坐标为(1,0),每一次将三角形AOB绕着点O逆时针方向旋转60°,同时每边扩大为原来的2倍,第一次旋转后得到△A1OB1,第二次旋转后得到△A2OB2……依此类推,则点A2021的坐标为 ( )
A.(-22020,-×22020)
B.(22021,-×22021)
C.(22020,-×22020)
D.(-22021,-×22021)
图Z1-15
C
[解析]由已知可得:
第一次旋转后,A1在第一象限,OA1=2,
第二次旋转后,A2在第二象限,OA2=22,
第三次旋转后,A3在x轴负半轴上,OA3=23,
第四次旋转后,A4在第三象限,OA4=24,
第五次旋转后,A5在第四象限,OA5=25,
第六次旋转后,A6在x轴正半轴上,OA6=26,
…
如此循环,每旋转6次,A的对应点又回到x轴正半轴上,
而2021=6×336+5,
∴A2021在第四象限,且OA2021=22021,示意图如图:
过点A2021作A2021H⊥x轴于H,
则OH=OA2021=22020,A2021H=OH=×22020,
∴A2021(22020,-×22020).
6.[2020·达州]已知k为正整数,无论k取何值,直线l1:y=kx+k+1与直线l2:y=(k+1)x+k+2都交于一个固定的点,这个点的坐标是
;记直线l1和l2与x轴围成的三角形面积为Sk,则S1=
,S1+S2+S3+…+S100的值为 .
(-1,1)
[解析]由题意得kx+k+1=(k+1)x+k+2,解得x=-1,将x=-1代入直线l1的解析式得y=1,所以交点为(-1,1).当k=1时,直线l1:y=x+2和直线l2:y=2x+3与x轴的交点分别为(-2,0)和(-,0),所以围成的三角形面积S1=×1=,依次可得:S2=,S3=,S4=,…,发现Sn=,
∴S1+S2+S3+…+S100=+…+(1-+…+)=(1-)=.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 01
规律探索型问题
一、常见的数列:
(1)正整数:1,2,3,4,5,…,第n项为n,前n项和为;
(2)奇数:1,3,5,7,…,第n项为2n-1,前n项和为n2;
(3)偶数:2,4,6,8,…,第n项为2n,前n项和为n(n+1);
(4)1,-1,1,-1,1,-1,…,第n项为(-1)n+1;-1,1,-1,1,-1,1,…,第n项为(-1)n;
(5)a,a+d,a+2d,a+3d,…,第n项为a+(n-1)d(特点:第一项为a,从第二项开始每一项比前一项增加d).
类型一
数式规律探索
二、解题策略
(1)分式型问题:分别观察分子、分母的特征及相邻项的变化规律;也可考虑先化异分母分式为同分母分式,再求解;
(2)乘积形式:分别表示,再相乘,如a,2a2,3a3,4a4,…,第n项可表示为nan;
(3)等式型问题:给等式标序号,分别用序号表示出等式的左右两边,代入序号验证.
1.[2021·云南]按一定规律排列的单项式:
a2,4a3,9a4,16a5,25a6,…,第n个单项式是 ( )
A.n2an+1 B.n2an-1
C.nnan+1 D.(n+1)2an
A
2.[2021·济宁]按规律排列的一组数据:,,□,,,…,其中□内应填的数是 ( )
A. B. C. D.
D
[解析]观察这组数据发现:分子为连续的奇数,分母为序号的平方+1,∴第n个数据为:.当n=3时,□的分子为5,分母=32+1=
10,∴这个数为.
3.[2021·甘肃省卷]一组按规律排列的代数式:a+2b,a2-2b3,
a3+2b5,a4-2b7,…,则第n个式子是 .
4.[2020·咸宁]按一定规律排列的一列数:3,32,3-1,33,3-4,37,3-11,
318,…,若a,b,c表示这列数中的连续三个数,猜想a,b,c满足的关系式是 .
an+(-1)n+1·2b2n-1
bc=a
[解析]一列数:3,32,3-1,33,3-4,37,3-11,318,…,可发现:第n个数等于前面两个数的商.∵a,b,c表示这列数中的连续三个数,∴bc=a,因此本题填bc=a.
5.[2020·张家界]观察下面的变化规律:=1-,,
,,…,
根据上面的规律计算:+…+= .
[解析]+…+=1-+…+
=1-.
6.古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,若把第一个三角形数记为x1,第二个三角形数记为x2,…,第n个三角形数记为xn,则xn+xn+1= .
(n+1)2
[解析]∵x1+x2=1+3=4;x2+x3=3+6=9;x3+x4=6+10=16;
x4+x5=10+15=25;x5+x6=15+21=36;…;∴xn+xn+1=(n+1)2.
7.[2021·随州]如图Z1-1,根据图中数字的规律,若第n个图中的q=143,则p的值为 ( )
A.100 B.121 C.144 D.169
图Z1-1
B
[解析]通过观察可得规律:p=n2,q=(n+1)2-1,
∵q=143,
∴(n+1)2-1=143,解得n=11(负值已舍),
∴p=n2=112=121.
8.[2021·怀化]观察等式:2+22=23-2,2+22+23=24-2,2+22+23+24=
25-2,…,已知按一定规律排列的一组数:2100,2101,2102,…,2199,若2100=m,用含m的代数式表示这组数的和是 .
m2-m
[解析]由题意得2100+2101+2102+…+2199=(2+22+23+…+2199)-(2+22+23+…+299)=(2200-2)-(2100-2)=(2100)2-2100=m2-m.
9.[2021·恩施州]古希腊数学家定义了五边形数,如下表所示,将点按照表中方式排列成五边形点阵,图形中的点的个数即五边形数.
图形 …
五边 形数 1 5 12 22 35 51 …
将五边形数1,5,12,22,35,51,…,排成如图Z1-2所示的数图:
观察这个数图,则这个数图中的第八行从左至右第2个数为
.
图Z1-2
1335
[解析]观察表中图形及数字的变化规律可得第n个五边形数可表示为:1+2+3+…+(n-1)+n2,
由数图可知前七行数的个数和为:1+2+3+…+7=28,
∴数图中的第八行从左至右第2个数是第30个五边形数,
即n=30,∴把n=30代入得
1+2+3+…+29+302=1335.
解决图形规律题的步骤:①标序数——按图号标序号;
②找规律——数出每一项的元素个数,将其表示成与序数有关的式子,用n表示出来;
③验证——代入序号验证所归纳的式子是否正确.
类型二
图形规律探索
1.[2020·重庆A卷]把黑色三角形按如图Z1-3所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形……按此规律排列下去,则第⑤个图案中黑色三角形的个数为 ( )
A.10 B.15 C.18 D.21
图Z1-3
B
[解析]本题考查了图形规律的探索,观察图形可知,第①个图案中黑色三角形个数为1,第②个图案中黑色三角形个数为3=1+2,第③个图案中黑色三角形个数为6=1+2+3,…,按此规律可知第⑤个图案中黑色三角形个数为1+2+3+4+5=15.
2.[2021·玉林]观察下列树枝分杈的规律图,若第n个图树枝数用Yn表示,则Y9-Y4= ( )
A.15×24 B.31×24 C.33×24 D.63×24
图Z1-4
B
[解析]由第1个图可知Y1=1=21-1,由第2个图可知Y2=3=22-1,由第3个图可知Y3=7=23-1,由第4个图可知Y4=15=24-1,
可知Yn=2n-1.即Y9=29-1,Y4=24-1.
因此Y9-Y4=29-1-(24-1)=29-24=24×(25-1)=31×24.
3.用若干大小相同的黑白两种颜色的正方形瓷砖,按下列规律铺成一列图案,则第7个图案中黑色瓷砖的个数是 ( )
A.19 B.20 C.21 D.22
图Z1-5
D
4.[2020·德州]下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案黑色棋子的个数是 ( )
A.148 B.152 C.174 D.202
图Z1-6
C
[解析]图①中的黑色棋子数是0+2×(1+2+3);图②中的黑色棋子数是2+2×(1+2+3+4);
图③中的黑色棋子数是4+2×(1+2+3+4+5);图④中的黑色棋子数是6+2×(1+2+3+4+5+6);…,
第10个这样的图案黑色棋子数是2×9+2×(1+2+3+4+5+6+…+11+12)
=18+2××12×(1+12)=174.
5.[2021·凉山州]如图Z1-7,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍;拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍……照这样拼图,则第n个图形需要 根火柴棍.
图Z1-7
(2n+1)
[解析]第一个图形需要火柴棍:3=1×2+1;
第二个图形需要火柴棍:5=2×2+1;
第三个图形需要火柴棍:7=3×2+1;…;
∴第n个图形需要火柴棍:2n+1.
6.[2020·牡丹江]如图Z1-8是由同样大小的圆按一定规律排列所组成的,其中第1个图形中一共有4个圆,第2个图形中一共有8个圆,第3个图形中一共有14个圆,第4个图形中一共有22个圆……按此规律排列下去,第9个图形中圆的个数是 个.
图Z1-8
92
[解析]根据已有图形找规律,第1个图形中一共有1×(1+1)+2=4个圆,第2个图形中一共有2×(2+1)+2=8个圆,第3个图形中一共有3×(3+1)+2=14个圆,第4个图形中一共有4×(4+1)+2=22个圆,故可得第n个图形中圆的个数是n(n+1)+2,所以第9个图形中圆的个数是9×(9+1)+2=92.
7.如图Z1-9,Rt△ABC中有n个正方形从左往右依次排开(每个正方形右上角的顶点均在AB边上,下方的两个顶点均在BC边上),第一个正方形的边长DF=9 cm,第二个正方形的边长GK=6 cm,
则从左往右第n个正方形的边长= cm.
图Z1-9
9×()n-1
[解析]∵第一个正方形的边长DF=9 cm,第二个正方形的边长GK=6 cm,
∴EF=9,∴GF=EF-EG=9-6=3,设PQ=x,
∵GK∥PQ,∴∠FKG=∠KQP.
又∵∠FGK=∠KPQ=90°,
∴△FGK∽△KPQ,∴,∴,解得x=4.
∵第二个正方形的边长为9×=6,第三个正方形的边长为9×()2=4,
∴第n个正方形的边长为9×()n-1.
8.如图Z1-10①是一个三角形,分别连接这个三角形三边的中点,得到图②,再分别连接图②中的小三角形三边的中点,得到图③.按此继续下去,请你根据每个图形中的三角形个数的规律,完成下列问题.
图Z1-10
(1)将下表填写完整:
(2)在第n个图形中有 个三角形(用含n的式子表示);
(3)第 个图形中有2021个三角形.
图形编号 1 2 3 4 5 …
三角形个数 1 5 9 …
图Z1-10
13
17
4n-3
506
坐标系中的规律问题,多为循环变化性问题,关键是依次正确求出前几步的结论,寻找点的横、纵坐标的变化规律,或者横、纵坐标之间的关系,或者找到循环规律.
类型三
坐标系中的规律探索
1.[2021·临沂]实验证实,放射性物质放出射线后,质量将减少,减少的速度开始较快,后来较慢,物质所剩的质量与时间成某种函数关系.如图Z1-11为表示镭的放射规律的函数图象,据此可计算32 mg镭缩减为1 mg所用的
时间大约是 ( )
A.4860年 B.6480年
C.8100年 D.9720年
图Z1-11
C
[解析]有m0→m0,0→1620,
m0→m0,1620→3240,
m0→m0,3240→4860,
∴每经过1620年,镭的质量就缩小到原来的一半,
有32 mg镭缩减为16 mg用时1620年,
16 mg镭缩减为8 mg用时1620年,
8 mg镭缩减为4 mg用时1620年,
4 mg镭缩减为2 mg用时1620年,
2 mg镭缩减为1 mg用时1620年,
∴32 mg镭缩减为1 mg用时1620×5=8100(年).
2.如图Z1-12,在平面直角坐标系中,将边长为1的正方形OABC绕点O顺时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2021次得到正方形OA2021B2021C2021,那么点A2021的坐标是 ( )
A.(,-) B.(1,0)
C.(-,-) D.(0,-1)
图Z1-12
C
[解析]∵四边形OABC是正方形,且OA=1,∴A(0,1),
∵正方形OABC绕点O依次顺时针旋转45°,
∴A1(,),A2(1,0),A3(,-),A4(0,-1),
A5(-,-),…
发现是8次一循环,∴2021÷8=252……5,
∴点A2021的坐标为(-,-),故选C.
3.[2021·仙桃]如图Z1-13,在平面直角坐标系中,动点P从原点O出发,水平向左平移1个单位长度,再竖直向下平移1个单位长度得点P1
(-1,-1);接着水平向右平移2个单位长度,再竖直向上平移2个单位长度得到点P2;接着水平向左平移3个单位长度,再竖直向下平移3个单位长度得到点P3;接着水平向右平移4
个单位长度,再竖直向上平移4个单位长度
得到点P4……按此作法进行下去,则点P2021
的坐标为 .
图Z1-13
(-1011,-1011)
[解析]先根据点坐标的平移变换规律求出点P2(1,1),P3(-2,-2),
P4(2,2),P5(-3,-3),归纳类推得:点P2n-1(-n,-n),其中n为正整数,
∵2021=2×1011-1,∴点P2021(-1011,-1011).
4.[2021·河北承德一模]如图Z1-14,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=A3A4=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记
△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3
于点B2,记△P2B2P3的面积为S3……依次
进行下去,则S3= ,最后记△Pn-1Bn-1Pn
(n>1)的面积为Sn,则Sn= .
图Z1-14
[解析]当x=1时,y=x2=,则P1(1,),所以S1=×1×;
当x=2时,y=x2=2,则P2(2,2),所以S2=×1×(2-)=;
当x=3时,y=x2=,则P3(3,),所以S3=×1×(-2)=;
同样方法可得S4=,所以Sn=.故答案为,.
5.[2021·达州]在平面直角坐标系中,等边三角形AOB如图Z1-15放置,点A的坐标为(1,0),每一次将三角形AOB绕着点O逆时针方向旋转60°,同时每边扩大为原来的2倍,第一次旋转后得到△A1OB1,第二次旋转后得到△A2OB2……依此类推,则点A2021的坐标为 ( )
A.(-22020,-×22020)
B.(22021,-×22021)
C.(22020,-×22020)
D.(-22021,-×22021)
图Z1-15
C
[解析]由已知可得:
第一次旋转后,A1在第一象限,OA1=2,
第二次旋转后,A2在第二象限,OA2=22,
第三次旋转后,A3在x轴负半轴上,OA3=23,
第四次旋转后,A4在第三象限,OA4=24,
第五次旋转后,A5在第四象限,OA5=25,
第六次旋转后,A6在x轴正半轴上,OA6=26,
…
如此循环,每旋转6次,A的对应点又回到x轴正半轴上,
而2021=6×336+5,
∴A2021在第四象限,且OA2021=22021,示意图如图:
过点A2021作A2021H⊥x轴于H,
则OH=OA2021=22020,A2021H=OH=×22020,
∴A2021(22020,-×22020).
6.[2020·达州]已知k为正整数,无论k取何值,直线l1:y=kx+k+1与直线l2:y=(k+1)x+k+2都交于一个固定的点,这个点的坐标是
;记直线l1和l2与x轴围成的三角形面积为Sk,则S1=
,S1+S2+S3+…+S100的值为 .
(-1,1)
[解析]由题意得kx+k+1=(k+1)x+k+2,解得x=-1,将x=-1代入直线l1的解析式得y=1,所以交点为(-1,1).当k=1时,直线l1:y=x+2和直线l2:y=2x+3与x轴的交点分别为(-2,0)和(-,0),所以围成的三角形面积S1=×1=,依次可得:S2=,S3=,S4=,…,发现Sn=,
∴S1+S2+S3+…+S100=+…+(1-+…+)=(1-)=.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
