2022中考数学三轮冲刺专题突破02 选填中的多解问题 课件(共56张ppt)
文档属性
| 名称 | 2022中考数学三轮冲刺专题突破02 选填中的多解问题 课件(共56张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:00:00 | ||
图片预览











文档简介
(共56张PPT)
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 02
选填中的多解问题
1.设a,b为非零实数,则的所有可能的值为 .
类型一
字母参数型多解问题
±2或0
[解析]①当a,b同号时,,也同号,即同为1或-1,故此时原式=±2;
②当a,b异号时,,也异号,即一个是1,另一个是-1,故此时原式=0.
所以所给代数式可能的值有3个:±2或0.
2.如果等式(2x-3)x+3=1,则等式成立的x值的个数为 .
3
[解析]当x+3=0,2x-3≠0时,x=-3;当2x-3=1时,x=2;当2x-3=-1时,
x=1,此时(2x-3)x+3=1,
∴x值的个数为3.
3.关于x的方程mx2m-1+(m-1)x-2=0,若是一元一次方程,则其解为 .
4.已知一次函数y=kx+b(k≠0)的图象经过点(2,0),且与坐标轴围
成的三角形的面积为1,则一次函数的解析式为____________
.
x=-3或x=-2或x=2
y=x-1或
y=-x+1
[解析]∵一次函数y=kx+b(k≠0)的图象经过点(2,0),
∴2k+b=0,b=-2k,∴y=kx-2k,
令x=0, 则y=-2k,令y=0,则x=2,
∵函数图象与两坐标轴围成的三角形面积为1,
∴×2×|-2k|=1,即|2k|=1,
解得:k=±,
则函数的解析式是y=x-1或y=-x+1.
5.若点A(m,n)在直线y=kx(k≠0)上,当-1≤m≤1时,-1≤n≤1,则这条直线的函数解析式为 .
y=x或y=-x
[解析]∵点A(m,n)在直线y=kx(k≠0)上,-1≤m≤1时,-1≤n≤1,
∴点(-1,-1),(1,1)在直线y=kx上,或点(1,-1),
(-1,1)在直线y=kx上,∴k=1或-1,
∴y=x或y=-x.
6.若关于x的函数y=(a+2)x2-(2a-1)x+a-2的图象与坐标轴有两
个交点,则a的值为 .
-2或2或
[解析]∵关于x的函数y=(a+2)x2-(2a-1)x+a-2的图象与坐标轴有两个交点,
∴可分如下三种情况:
①当函数为一次函数时,有a+2=0,
∴a=-2,此时y=5x-4,与坐标轴有两个交点;
②当函数为二次函数(a≠-2)时,其图象与x轴有一个交点,与y轴有一个交点,
∵函数图象与x轴有一个交点,∴Δ=0,
∴[-(2a-1)]2-4(a+2)(a-2)=0,解得a=;
③当函数为二次函数(a≠-2)时,其图象与x轴有两个交点,其中一个交点是坐标原点,即图象经过原点,∴a-2=0,a=2.故答案为-2或2或.
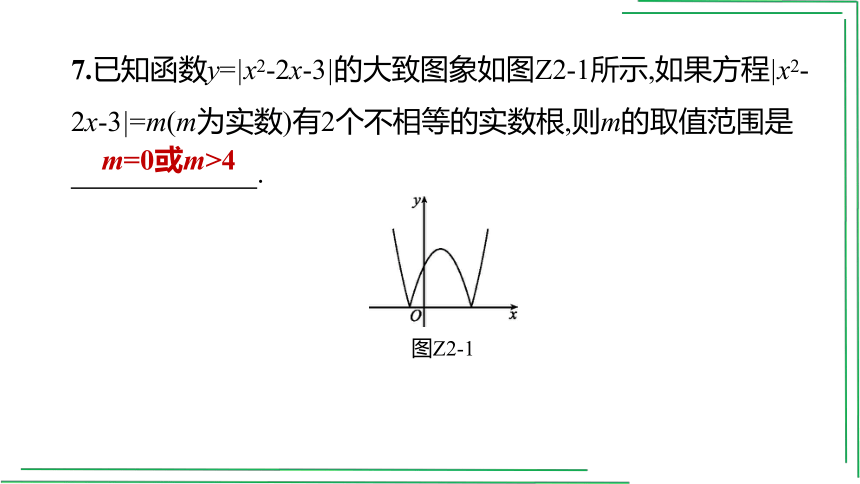
7.已知函数y=|x2-2x-3|的大致图象如图Z2-1所示,如果方程|x2-2x-3|=m(m为实数)有2个不相等的实数根,则m的取值范围是
.
图Z2-1
m=0或m>4
[解析]从图象可以看出,当y=0时,y=|x2-2x-3|的图象与x轴有两个不同的交点,即m=0时,方程|x2-2x-3|=m(m为实数)有2个不相等的实数根;|x2-2x-3|=|(x-1)2-4|,所以当m>4时,方程|x2-2x-3|=m
(m为实数)有2个不相等的实数根.
综上所述,当m=0或m>4时,方程|x2-2x-3|
=m(m为实数)有2个不相等的实数根.
故答案为m=0或m>4.
8.[2020·荆州]我们约定:(a,b,c)为函数y=ax2+bx+c的“关联数”,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”.若关联数为(m,-m-2,2)的函数图象与x轴有两个整交点(m为正整数),则这个函数图象上整交点的坐标为
.
(1,0),(2,0),(0,2)
[解析]由题意,得:“关联数”(m,-m-2,2)对应的函数解析式为y=mx2+(-m-2)x+2,
∴该函数图象与y轴有一个整交点,其坐标为(0,2),
∵该函数图象与x轴有两个整交点,
∴mx2-(m+2)x+2=0,
(mx-2)(x-1)=0,解得:x1=,x2=1.
∵m为正整数,∴m=2或m=1,
当m=2时,x1=x2=1,此时函数图象与x轴只有一个整交点,故舍去;
当m=1时,x1=2,此时函数图象与x轴的两个整交点坐标分别为(1,0),(2,0),
∴该函数图象与坐标轴的整交点坐标分别为(1,0),(2,0),(0,2).
9.如图Z2-2,已知直线y=-x+3分别交x轴,y轴于点A,B,P是抛物线y=-x2+2x+5上的一个动点,其横坐标为a,若过点P且平行于y轴的直线交直线y=-x+3于点Q,则当
PQ=BQ时,a的值可以是___________
.
图Z2-2
4或-1或
4+2或4-2
[解析]因为直线y=-x+3分别交x轴,y轴于点A,B,所以B(0,3),因为P是抛物线y=-x2+2x+5上的一个动点,其横坐标为a,所以P(a,-a2+2a+5),因为过点P且平行于y轴的直线交直线y=-x+3于点Q,所以Q(a,-a+3),
因为PQ平行于y轴,
10.二次函数y=ax2-x+c(a,c为常数)的图象经过点(1,7).
(1)c= ;(用含a的代数式表示)
(2)若该函数图象与x轴有两个交点,且只有一个交点在(2,0)与
(3,0)之间,则a的取值范围是 .
8-a
-2[解析](2)当x=2时,y=3a+6;当x=3时,y=8a+5,由211.已知二次函数y=-(x-h)2(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为-4,则h的值为 .
-1或5
[解析]∵二次函数y=-(x-h)2(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为-4,
∴当h≤1时,x=1时,y取得最大值-4,
即-4=-(1-h)2,解得h1=3(舍去),h2=-1;
当1当h≥3时,x=3时,y取得最大值-4,
即-4=-(3-h)2,解得h3=1(舍去),h4=5;
综上可得,h的值是-1或5.
12.[2020·宿迁模拟]已知二次函数y=x2+2x+n,当自变量x的取值在-2≤x≤1的范围内时,函数的图象与x轴有且只有一个公共点,则n的取值范围是 .
n=1或-3≤n<0
[解析]抛物线的对称轴为直线x=-=-1,若抛物线与x轴有一个交点,则当x=-1时,y=0;当x=1,y≥0且x=-2,y<0时,在-2≤x≤1的范围内,抛物线与x轴有且只有一个公共点,即1+2+n≥0且4-4+n<0,解得-3≤n<0.所以n的取值范围是n=1或-3≤n<0.
13.抛物线y=x2+2ax-3与x轴交于A,B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是 .
0[解析]∵抛物线y=x2+2ax-3与x轴交于A,B(1,0)两点(点A在点B的左侧),
∴1+2a-3=0,得a=1,
∴y=x2+2x-3=(x+3)(x-1),
当y=0时,x1=-3,x2=1,∴点A的坐标为(-3,0),
∵将抛物线沿y轴平移m(m>0)个单位,
∴平移后的抛物线解析式为y=x2+2x-3+m=(x+1)2-4+m,
∴当平移后的抛物线过点(0,0)时,0=(0+1)2-4+m,得m=3,
当平移后抛物线的顶点在x轴上时,抛物线与线段OA有一个交点,即0=(-1+1)2-4+m,得m=4,
∵将抛物线沿y轴平移m(m>0)个单位,平移后的抛物线与线段OA有且只有一个交点,∴014.[2020·嘉兴]已知二次函数y=x2,当a≤x≤b时,m≤y≤n,则下列说法正确的是 ( )
A.当n-m=1时,b-a有最小值
B.当n-m=1时,b-a有最大值
C.当b-a=1时,n-m无最小值
D.当b-a=1时,n-m有最大值
B
[解析]①当b-a=1时,当a,b同号时,如图①,过点B作BC⊥AD于C,
易得四边形BCDE是矩形,
∴BC=DE=b-a=1,CD=BE=m,
∴AC=AD-CD=n-m,
在Rt△ACB中,tan∠ABC==n-m,
∵点A,B在抛物线y=x2上,且a,b同号,
∴45°≤∠ABC<90°,
∴tan∠ABC≥1,∴n-m≥1,
当a,b异号时,m=0,
当a=-,b=时,n=,此时,n-m=,
∴≤n-m<1,即n-m≥,
即n-m无最大值,有最小值,最小值为,故选项C,D都错误;
②当n-m=1时,如图②,当a,b同号时,过点N作NH⊥MQ于H,
同①的方法得,NH=PQ=b-a,HQ=PN=m,
∴MH=MQ-HQ=n-m=1,
在Rt△MHN中,tan∠MNH=.
∵点M,N在抛物线y=x2上,
∴m≥0,当m=0时,n=1,∴点N(0,0),M(1,1),
此时,∠MNH=45°,
∴45°≤∠MNH<90°,∴tan∠MNH≥1,∴≥1,
当a,b异号时,m=0,∴n=1,∴a=-1,b=1,
即b-a=2,
∴b-a无最小值,有最大值,最大值为2,
故选项A错误.故选B.
1.[2021·绍兴]如图Z2-3,在△ABC中,AB=AC,∠B=70°,以点C为圆心,CA长为半径作弧,交直线BC于点P,连接AP,则∠BAP的度数是 .
类型二
图形的形状和位置不确定型多解问题
图Z2-3
15°或75°
[解析]如图所示,当点P在点B的左侧时,
∵AB=AC,∠ABC=70°,∴∠ACB=∠ABC=70°,
∴∠BAC=180°-∠ACB-∠ABC=180°-70°-70°=40°.
∵CA=CP1,∴∠CAP1=∠CP1A==55°,
∴∠BAP1=∠CAP1-∠CAB=55°-40°=15°;
当点P在点C的右侧时,∵CA=CP2,∴∠CAP2=∠CP2A==35°,
∴∠BAP2=∠CAP2+∠CAB=35°+40°=75°.
综上可得,∠BAP的度数是15°或75°.
2.[2021·乐山]在Rt△ABC中,∠C=90°,有一个锐角为60°,AB=4.若点P在直线AB上(不与点A,B重合),且∠PCB=30°,则CP的长为 .
2或或2
[解析](1)当∠ABC=60°时,则BC=AB=2,
当点P在线段AB上时,
∵∠PCB=30°,∴CP⊥AB,
∴PC=BCcos30°=2×;
当点P(P')在AB的延长线上时,
∵∠P'CB=30°,∠ABC=60°,∴∠P'=30°,
∴△P'BC为等腰三角形,∴BP'=BC=2,
∴P'C=2BCcos30°=2;
(2)当∠BAC=60°时,同理可得,PC=2.
3.[2019·荆州]如图Z2-4,AB为☉O的直径,C为☉O上一点,过B点的切线交AC的延长线于点D,E为弦AC的中点,AD=10,BD=6,若点P为直径AB上的一个动点,连接EP,当△AEP是直角三角形时,AP的长为 .
图Z2-4
4或2.56
[解析]∵过B点的切线交AC的延长线于点D,∴AB⊥BD,
∴AB==8,
当∠AEP=90°时,∵AE=EC,∴EP经过圆心O,
∴AP=AO=4;
当∠APE=90°时,EP∥BD,∴,
连接OE,易得△AEO∽△ABD,∴,即,
∴AE=3.2,∴,∴AP=2.56.
综上,AP的长为4或2.56.
4.如图Z2-5,在△ABC中,AB=3,BC=3,AC=6,点D是AC上一个动点,过点D作DF⊥BC于点F,过点F作FE∥AC,交AB于点E.
(1)当四边形ADFE为菱形时,则∠AED= ;
(2)当△DEF为直角三角形时,则CD= .
图Z2-5
60°
3或
[解析](2)由题意可得△ABC为直角三角形,四边形DFEA为平行四边形,当∠FDE为直角时,设DF=x,则AE=x,BE=3-x,所以x=3-x,
x=,CD=2x=3;当∠DEF为直角时,AD=6-2x,AE=x,
所以6-2x=x·cos60°,解得x=,即CD=.
5.[2019·龙东地区]一张直角三角形纸片ABC,∠ACB=90°,AB=
10,AC=6,点D为BC边上的任一点,沿过点D的直线折叠,使直角顶点C落在斜边AB上的点E处,当△BDE是直角三角形时,CD的
长为 .
3或
[解析]如图①,∠DEB是直角时,
∵∠ACB=90°,AB=10,AC=6,∴BC==8,
设CD=x,则BD=8-x,由折叠知CD=ED=x,
∵∠ACB=∠DEB=90°,∠B=∠B,
∴△BED∽△BCA,∴,即,解得x=3;
如图②,∠EDB是直角时,ED∥AC,∴△BED∽△BAC,
∴,设CD=y,则BD=8-y,
∴,解得y=,综上,CD的长为3或.
6.如图Z2-6,在平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB所得的三角形
与△AOB相似,那么点P的坐标是 .
图Z2-6
(0,3)或(4,0)或(,0)
[解析]当PC∥OA时,△BPC∽△BOA,由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(0,3);
当PC∥OB时,△ACP∽△ABO,由点C是AB的中点,可得P为OA的中点,此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵点A(8,0)和点B(0,6),
∴AB==10,
∵点C是AB的中点,∴AC=5.
∵∠CAP=∠OAB,∴Rt△APC∽Rt△ABO,
∴,∴,∴AP=,
∴OP=OA-AP=8-,此时P点坐标为(,0).
综上所述,满足条件的P点坐标为(0,3)或(4,0)或(,0).
7.[2019·菏泽]如图Z2-7,直线y=-x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作☉P,
当☉P与直线AB相切时,点P的坐标是 .
图Z2-7
(-,0)或(-,0)
[解析]∵直线y=-x-3交x轴于点A,交y轴于点B,
∴令x=0,得y=-3,令y=0,得x=-4,
∴A(-4,0),B(0,-3),
∴OA=4,OB=3,∴AB=5,
如图,设☉P与直线AB相切于点D,
连接PD,则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,∠PAD=∠BAO,
∴△APD∽△ABO,
∴,∴,∴AP=,
∴OP=或OP=,
∴P点坐标为(-,0)或(-,0),
故答案为:(-,0)或(-,0).
8.如图Z2-8,大正方形ABCD中,AB=5,小正方形AEFG中,AE=,在小正方形绕A点旋转的过程中,当∠EFC=90°时,线段BE的长为 .
图Z2-8
或2
[解析]如图①,连接AF,AC,则,
又∠BAE=∠CAF=45°-∠EAC,
∴△ABE∽△ACF,∴.
∵∠EFC=90°,
∴在Rt△ACG中,根据勾股定理,得CG==3.∴CF=CG-GF=2,∴,即BE=;
如图②,连接AF,AC,同理易得△ABE∽△ACF,
∴,又CF=CG+FG=4,
∴,即BE=2.
9.[2021·云南]已知△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D.若△ABC的一条边长为
6,则点D到直线AB的距离为 .
或3或6-6或6-3
[解析]①当B为直角顶点时,过D作DH⊥AB于H,如图:
∵△ABC的三个顶点都是同一个
正方形的顶点,∠ABC的平分线
与线段AC交于点D,
∴△ABC是等腰直角三角形,∠ABD=∠ADH=45°,AD=CD=AC,
∴△AHD和△BHD是等腰直角三角形,
∴AH=DH=BH,∴DH=BC,
若AC=6,则BC=AC·cos45°=3,
此时DH=,即点D到直线AB的距离为;
若AB=BC=6,则DH=BC=3,即点D到直线AB的距离为3;
②当B不是直角顶点时,过D作DH⊥BC于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△CDH是等腰直角三角形,AD=DH=CH,
在△ABD和△HBD中,
∴△ABD≌△HBD(AAS),∴AB=BH,
若AB=AC=6,则BH=6,BC==6,
∴CH=BC-BH=6-6,
∴AD=6-6,即此时点D到直线AB的距离为6-6;
若BC=6,则AB=BC·cos45°=3,∴BH=3,
∴CH=6-3,
∴AD=6-3,即此时点D到直线AB的距离为6-3.
综上所述,点D到直线AB的距离为或3或6-6或6-3.
10.在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30 cm.将该纸片沿过点B的直线折叠,使点A落在斜边BC上的点E处,折痕记为BD(如图Z2-9①),剪去△CDE后得到双层△BDE(如图②),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,
则所得平行四边形的周长为
cm.
图Z2-9
40或
[解析]由折叠知AD=DE,∠CAB=∠BED=∠CED=90°,
又∠C=30°,得DE=CD=AC=10=AD.
分两种情况:(1)如图①,过点E作EF∥AC
交BD于点F,连接AF,得到平行四边形
DEFA,此时四边形DEFA为菱形,周长
为4AD=40 cm;
(2)如图②,过点D分别作AB,BC的平行线,交BC于点H,交AB于点G,得到平行四边形DHBG,此时也为菱形,由DG∥BC,得∠ADG=∠C=30°,
在Rt△ADG中,DG=,
∴平行四边形DHBG的周长=4DG=(cm).
故填40或.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 02
选填中的多解问题
1.设a,b为非零实数,则的所有可能的值为 .
类型一
字母参数型多解问题
±2或0
[解析]①当a,b同号时,,也同号,即同为1或-1,故此时原式=±2;
②当a,b异号时,,也异号,即一个是1,另一个是-1,故此时原式=0.
所以所给代数式可能的值有3个:±2或0.
2.如果等式(2x-3)x+3=1,则等式成立的x值的个数为 .
3
[解析]当x+3=0,2x-3≠0时,x=-3;当2x-3=1时,x=2;当2x-3=-1时,
x=1,此时(2x-3)x+3=1,
∴x值的个数为3.
3.关于x的方程mx2m-1+(m-1)x-2=0,若是一元一次方程,则其解为 .
4.已知一次函数y=kx+b(k≠0)的图象经过点(2,0),且与坐标轴围
成的三角形的面积为1,则一次函数的解析式为____________
.
x=-3或x=-2或x=2
y=x-1或
y=-x+1
[解析]∵一次函数y=kx+b(k≠0)的图象经过点(2,0),
∴2k+b=0,b=-2k,∴y=kx-2k,
令x=0, 则y=-2k,令y=0,则x=2,
∵函数图象与两坐标轴围成的三角形面积为1,
∴×2×|-2k|=1,即|2k|=1,
解得:k=±,
则函数的解析式是y=x-1或y=-x+1.
5.若点A(m,n)在直线y=kx(k≠0)上,当-1≤m≤1时,-1≤n≤1,则这条直线的函数解析式为 .
y=x或y=-x
[解析]∵点A(m,n)在直线y=kx(k≠0)上,-1≤m≤1时,-1≤n≤1,
∴点(-1,-1),(1,1)在直线y=kx上,或点(1,-1),
(-1,1)在直线y=kx上,∴k=1或-1,
∴y=x或y=-x.
6.若关于x的函数y=(a+2)x2-(2a-1)x+a-2的图象与坐标轴有两
个交点,则a的值为 .
-2或2或
[解析]∵关于x的函数y=(a+2)x2-(2a-1)x+a-2的图象与坐标轴有两个交点,
∴可分如下三种情况:
①当函数为一次函数时,有a+2=0,
∴a=-2,此时y=5x-4,与坐标轴有两个交点;
②当函数为二次函数(a≠-2)时,其图象与x轴有一个交点,与y轴有一个交点,
∵函数图象与x轴有一个交点,∴Δ=0,
∴[-(2a-1)]2-4(a+2)(a-2)=0,解得a=;
③当函数为二次函数(a≠-2)时,其图象与x轴有两个交点,其中一个交点是坐标原点,即图象经过原点,∴a-2=0,a=2.故答案为-2或2或.
7.已知函数y=|x2-2x-3|的大致图象如图Z2-1所示,如果方程|x2-2x-3|=m(m为实数)有2个不相等的实数根,则m的取值范围是
.
图Z2-1
m=0或m>4
[解析]从图象可以看出,当y=0时,y=|x2-2x-3|的图象与x轴有两个不同的交点,即m=0时,方程|x2-2x-3|=m(m为实数)有2个不相等的实数根;|x2-2x-3|=|(x-1)2-4|,所以当m>4时,方程|x2-2x-3|=m
(m为实数)有2个不相等的实数根.
综上所述,当m=0或m>4时,方程|x2-2x-3|
=m(m为实数)有2个不相等的实数根.
故答案为m=0或m>4.
8.[2020·荆州]我们约定:(a,b,c)为函数y=ax2+bx+c的“关联数”,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”.若关联数为(m,-m-2,2)的函数图象与x轴有两个整交点(m为正整数),则这个函数图象上整交点的坐标为
.
(1,0),(2,0),(0,2)
[解析]由题意,得:“关联数”(m,-m-2,2)对应的函数解析式为y=mx2+(-m-2)x+2,
∴该函数图象与y轴有一个整交点,其坐标为(0,2),
∵该函数图象与x轴有两个整交点,
∴mx2-(m+2)x+2=0,
(mx-2)(x-1)=0,解得:x1=,x2=1.
∵m为正整数,∴m=2或m=1,
当m=2时,x1=x2=1,此时函数图象与x轴只有一个整交点,故舍去;
当m=1时,x1=2,此时函数图象与x轴的两个整交点坐标分别为(1,0),(2,0),
∴该函数图象与坐标轴的整交点坐标分别为(1,0),(2,0),(0,2).
9.如图Z2-2,已知直线y=-x+3分别交x轴,y轴于点A,B,P是抛物线y=-x2+2x+5上的一个动点,其横坐标为a,若过点P且平行于y轴的直线交直线y=-x+3于点Q,则当
PQ=BQ时,a的值可以是___________
.
图Z2-2
4或-1或
4+2或4-2
[解析]因为直线y=-x+3分别交x轴,y轴于点A,B,所以B(0,3),因为P是抛物线y=-x2+2x+5上的一个动点,其横坐标为a,所以P(a,-a2+2a+5),因为过点P且平行于y轴的直线交直线y=-x+3于点Q,所以Q(a,-a+3),
因为PQ平行于y轴,
10.二次函数y=ax2-x+c(a,c为常数)的图象经过点(1,7).
(1)c= ;(用含a的代数式表示)
(2)若该函数图象与x轴有两个交点,且只有一个交点在(2,0)与
(3,0)之间,则a的取值范围是 .
8-a
-2
-1或5
[解析]∵二次函数y=-(x-h)2(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为-4,
∴当h≤1时,x=1时,y取得最大值-4,
即-4=-(1-h)2,解得h1=3(舍去),h2=-1;
当1
即-4=-(3-h)2,解得h3=1(舍去),h4=5;
综上可得,h的值是-1或5.
12.[2020·宿迁模拟]已知二次函数y=x2+2x+n,当自变量x的取值在-2≤x≤1的范围内时,函数的图象与x轴有且只有一个公共点,则n的取值范围是 .
n=1或-3≤n<0
[解析]抛物线的对称轴为直线x=-=-1,若抛物线与x轴有一个交点,则当x=-1时,y=0;当x=1,y≥0且x=-2,y<0时,在-2≤x≤1的范围内,抛物线与x轴有且只有一个公共点,即1+2+n≥0且4-4+n<0,解得-3≤n<0.所以n的取值范围是n=1或-3≤n<0.
13.抛物线y=x2+2ax-3与x轴交于A,B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是 .
0
∴1+2a-3=0,得a=1,
∴y=x2+2x-3=(x+3)(x-1),
当y=0时,x1=-3,x2=1,∴点A的坐标为(-3,0),
∵将抛物线沿y轴平移m(m>0)个单位,
∴平移后的抛物线解析式为y=x2+2x-3+m=(x+1)2-4+m,
∴当平移后的抛物线过点(0,0)时,0=(0+1)2-4+m,得m=3,
当平移后抛物线的顶点在x轴上时,抛物线与线段OA有一个交点,即0=(-1+1)2-4+m,得m=4,
∵将抛物线沿y轴平移m(m>0)个单位,平移后的抛物线与线段OA有且只有一个交点,∴0
A.当n-m=1时,b-a有最小值
B.当n-m=1时,b-a有最大值
C.当b-a=1时,n-m无最小值
D.当b-a=1时,n-m有最大值
B
[解析]①当b-a=1时,当a,b同号时,如图①,过点B作BC⊥AD于C,
易得四边形BCDE是矩形,
∴BC=DE=b-a=1,CD=BE=m,
∴AC=AD-CD=n-m,
在Rt△ACB中,tan∠ABC==n-m,
∵点A,B在抛物线y=x2上,且a,b同号,
∴45°≤∠ABC<90°,
∴tan∠ABC≥1,∴n-m≥1,
当a,b异号时,m=0,
当a=-,b=时,n=,此时,n-m=,
∴≤n-m<1,即n-m≥,
即n-m无最大值,有最小值,最小值为,故选项C,D都错误;
②当n-m=1时,如图②,当a,b同号时,过点N作NH⊥MQ于H,
同①的方法得,NH=PQ=b-a,HQ=PN=m,
∴MH=MQ-HQ=n-m=1,
在Rt△MHN中,tan∠MNH=.
∵点M,N在抛物线y=x2上,
∴m≥0,当m=0时,n=1,∴点N(0,0),M(1,1),
此时,∠MNH=45°,
∴45°≤∠MNH<90°,∴tan∠MNH≥1,∴≥1,
当a,b异号时,m=0,∴n=1,∴a=-1,b=1,
即b-a=2,
∴b-a无最小值,有最大值,最大值为2,
故选项A错误.故选B.
1.[2021·绍兴]如图Z2-3,在△ABC中,AB=AC,∠B=70°,以点C为圆心,CA长为半径作弧,交直线BC于点P,连接AP,则∠BAP的度数是 .
类型二
图形的形状和位置不确定型多解问题
图Z2-3
15°或75°
[解析]如图所示,当点P在点B的左侧时,
∵AB=AC,∠ABC=70°,∴∠ACB=∠ABC=70°,
∴∠BAC=180°-∠ACB-∠ABC=180°-70°-70°=40°.
∵CA=CP1,∴∠CAP1=∠CP1A==55°,
∴∠BAP1=∠CAP1-∠CAB=55°-40°=15°;
当点P在点C的右侧时,∵CA=CP2,∴∠CAP2=∠CP2A==35°,
∴∠BAP2=∠CAP2+∠CAB=35°+40°=75°.
综上可得,∠BAP的度数是15°或75°.
2.[2021·乐山]在Rt△ABC中,∠C=90°,有一个锐角为60°,AB=4.若点P在直线AB上(不与点A,B重合),且∠PCB=30°,则CP的长为 .
2或或2
[解析](1)当∠ABC=60°时,则BC=AB=2,
当点P在线段AB上时,
∵∠PCB=30°,∴CP⊥AB,
∴PC=BCcos30°=2×;
当点P(P')在AB的延长线上时,
∵∠P'CB=30°,∠ABC=60°,∴∠P'=30°,
∴△P'BC为等腰三角形,∴BP'=BC=2,
∴P'C=2BCcos30°=2;
(2)当∠BAC=60°时,同理可得,PC=2.
3.[2019·荆州]如图Z2-4,AB为☉O的直径,C为☉O上一点,过B点的切线交AC的延长线于点D,E为弦AC的中点,AD=10,BD=6,若点P为直径AB上的一个动点,连接EP,当△AEP是直角三角形时,AP的长为 .
图Z2-4
4或2.56
[解析]∵过B点的切线交AC的延长线于点D,∴AB⊥BD,
∴AB==8,
当∠AEP=90°时,∵AE=EC,∴EP经过圆心O,
∴AP=AO=4;
当∠APE=90°时,EP∥BD,∴,
连接OE,易得△AEO∽△ABD,∴,即,
∴AE=3.2,∴,∴AP=2.56.
综上,AP的长为4或2.56.
4.如图Z2-5,在△ABC中,AB=3,BC=3,AC=6,点D是AC上一个动点,过点D作DF⊥BC于点F,过点F作FE∥AC,交AB于点E.
(1)当四边形ADFE为菱形时,则∠AED= ;
(2)当△DEF为直角三角形时,则CD= .
图Z2-5
60°
3或
[解析](2)由题意可得△ABC为直角三角形,四边形DFEA为平行四边形,当∠FDE为直角时,设DF=x,则AE=x,BE=3-x,所以x=3-x,
x=,CD=2x=3;当∠DEF为直角时,AD=6-2x,AE=x,
所以6-2x=x·cos60°,解得x=,即CD=.
5.[2019·龙东地区]一张直角三角形纸片ABC,∠ACB=90°,AB=
10,AC=6,点D为BC边上的任一点,沿过点D的直线折叠,使直角顶点C落在斜边AB上的点E处,当△BDE是直角三角形时,CD的
长为 .
3或
[解析]如图①,∠DEB是直角时,
∵∠ACB=90°,AB=10,AC=6,∴BC==8,
设CD=x,则BD=8-x,由折叠知CD=ED=x,
∵∠ACB=∠DEB=90°,∠B=∠B,
∴△BED∽△BCA,∴,即,解得x=3;
如图②,∠EDB是直角时,ED∥AC,∴△BED∽△BAC,
∴,设CD=y,则BD=8-y,
∴,解得y=,综上,CD的长为3或.
6.如图Z2-6,在平面直角坐标系中,已知点A(8,0)和点B(0,6),点C是AB的中点,点P在折线AOB上,直线CP截△AOB所得的三角形
与△AOB相似,那么点P的坐标是 .
图Z2-6
(0,3)或(4,0)或(,0)
[解析]当PC∥OA时,△BPC∽△BOA,由点C是AB的中点,可得P为OB的中点,
此时P点坐标为(0,3);
当PC∥OB时,△ACP∽△ABO,由点C是AB的中点,可得P为OA的中点,此时P点坐标为(4,0);
当PC⊥AB时,如图,
∵点A(8,0)和点B(0,6),
∴AB==10,
∵点C是AB的中点,∴AC=5.
∵∠CAP=∠OAB,∴Rt△APC∽Rt△ABO,
∴,∴,∴AP=,
∴OP=OA-AP=8-,此时P点坐标为(,0).
综上所述,满足条件的P点坐标为(0,3)或(4,0)或(,0).
7.[2019·菏泽]如图Z2-7,直线y=-x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作☉P,
当☉P与直线AB相切时,点P的坐标是 .
图Z2-7
(-,0)或(-,0)
[解析]∵直线y=-x-3交x轴于点A,交y轴于点B,
∴令x=0,得y=-3,令y=0,得x=-4,
∴A(-4,0),B(0,-3),
∴OA=4,OB=3,∴AB=5,
如图,设☉P与直线AB相切于点D,
连接PD,则PD⊥AB,PD=1,
∵∠ADP=∠AOB=90°,∠PAD=∠BAO,
∴△APD∽△ABO,
∴,∴,∴AP=,
∴OP=或OP=,
∴P点坐标为(-,0)或(-,0),
故答案为:(-,0)或(-,0).
8.如图Z2-8,大正方形ABCD中,AB=5,小正方形AEFG中,AE=,在小正方形绕A点旋转的过程中,当∠EFC=90°时,线段BE的长为 .
图Z2-8
或2
[解析]如图①,连接AF,AC,则,
又∠BAE=∠CAF=45°-∠EAC,
∴△ABE∽△ACF,∴.
∵∠EFC=90°,
∴在Rt△ACG中,根据勾股定理,得CG==3.∴CF=CG-GF=2,∴,即BE=;
如图②,连接AF,AC,同理易得△ABE∽△ACF,
∴,又CF=CG+FG=4,
∴,即BE=2.
9.[2021·云南]已知△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D.若△ABC的一条边长为
6,则点D到直线AB的距离为 .
或3或6-6或6-3
[解析]①当B为直角顶点时,过D作DH⊥AB于H,如图:
∵△ABC的三个顶点都是同一个
正方形的顶点,∠ABC的平分线
与线段AC交于点D,
∴△ABC是等腰直角三角形,∠ABD=∠ADH=45°,AD=CD=AC,
∴△AHD和△BHD是等腰直角三角形,
∴AH=DH=BH,∴DH=BC,
若AC=6,则BC=AC·cos45°=3,
此时DH=,即点D到直线AB的距离为;
若AB=BC=6,则DH=BC=3,即点D到直线AB的距离为3;
②当B不是直角顶点时,过D作DH⊥BC于H,如图:
∵△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D,
∴△CDH是等腰直角三角形,AD=DH=CH,
在△ABD和△HBD中,
∴△ABD≌△HBD(AAS),∴AB=BH,
若AB=AC=6,则BH=6,BC==6,
∴CH=BC-BH=6-6,
∴AD=6-6,即此时点D到直线AB的距离为6-6;
若BC=6,则AB=BC·cos45°=3,∴BH=3,
∴CH=6-3,
∴AD=6-3,即此时点D到直线AB的距离为6-3.
综上所述,点D到直线AB的距离为或3或6-6或6-3.
10.在三角形纸片ABC中,∠A=90°,∠C=30°,AC=30 cm.将该纸片沿过点B的直线折叠,使点A落在斜边BC上的点E处,折痕记为BD(如图Z2-9①),剪去△CDE后得到双层△BDE(如图②),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,
则所得平行四边形的周长为
cm.
图Z2-9
40或
[解析]由折叠知AD=DE,∠CAB=∠BED=∠CED=90°,
又∠C=30°,得DE=CD=AC=10=AD.
分两种情况:(1)如图①,过点E作EF∥AC
交BD于点F,连接AF,得到平行四边形
DEFA,此时四边形DEFA为菱形,周长
为4AD=40 cm;
(2)如图②,过点D分别作AB,BC的平行线,交BC于点H,交AB于点G,得到平行四边形DHBG,此时也为菱形,由DG∥BC,得∠ADG=∠C=30°,
在Rt△ADG中,DG=,
∴平行四边形DHBG的周长=4DG=(cm).
故填40或.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
