2022中考数学三轮冲刺专题突破03 函数实际应用问题 课件(共92张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺专题突破03 函数实际应用问题 课件(共92张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:00:00 | ||
图片预览







文档简介
(共92张PPT)
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 03
函数实际应用问题
●方法点析
●题型精练
●题型分类
函数实际应用型问题是把实际生活情境中的数量关系抽象为函数模型(如一次函数、二次函数、反比例函数以及它们的分段函数),进而应用函数知识进行分析、研究、解决的有关问题,求解此类问题的关键是把实际问题中的等量关系转化为两个变量之间的关系,重在考查数学应用意识和建模能力.
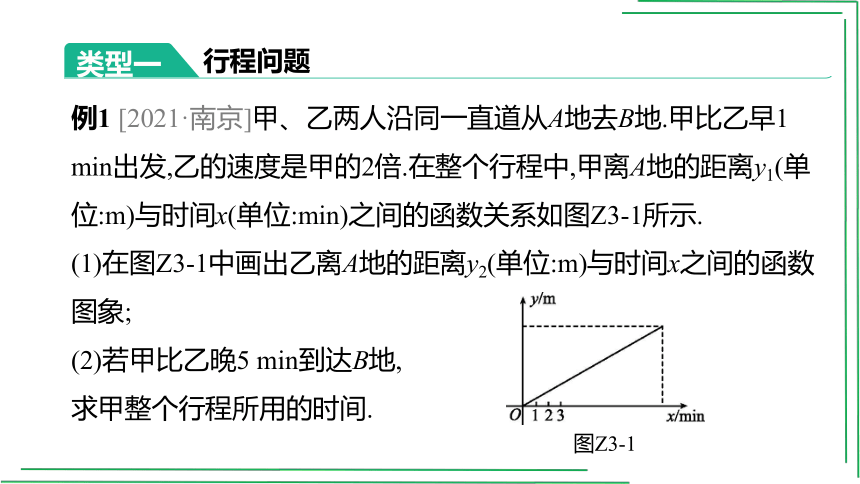
例1 [2021·南京]甲、乙两人沿同一直道从A地去B地.甲比乙早1 min出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离y1(单位:m)与时间x(单位:min)之间的函数关系如图Z3-1所示.
(1)在图Z3-1中画出乙离A地的距离y2(单位:m)与时间x之间的函数图象;
(2)若甲比乙晚5 min到达B地,
求甲整个行程所用的时间.
类型一
行程问题
图Z3-1
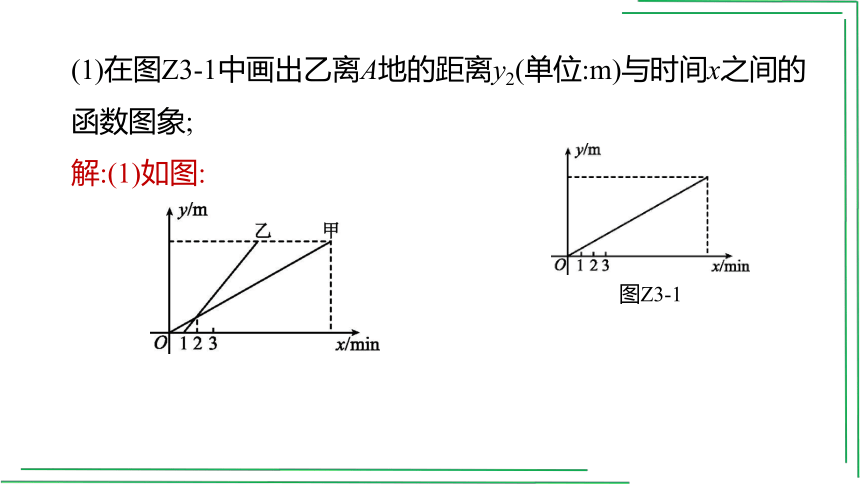
(1)在图Z3-1中画出乙离A地的距离y2(单位:m)与时间x之间的函数图象;
解:(1)如图:
图Z3-1
(2)若甲比乙晚5 min到达B地,求甲整个行程所用的时间.
(2)设甲的速度是v m/min,乙整个行程所用的时间为t min,
由题意得:2v·t=(t+1+5)v,解得:t=6,6+1+5=12(min),
答:甲整个行程所用的时间为12 min.
【方法点析】求解此类问题的关键是分析出图中的关键点对应的时间和路程,以及分段函数图象与实际情况的对应关系,进而根据图象中的数据解决问题.
|题型精练|
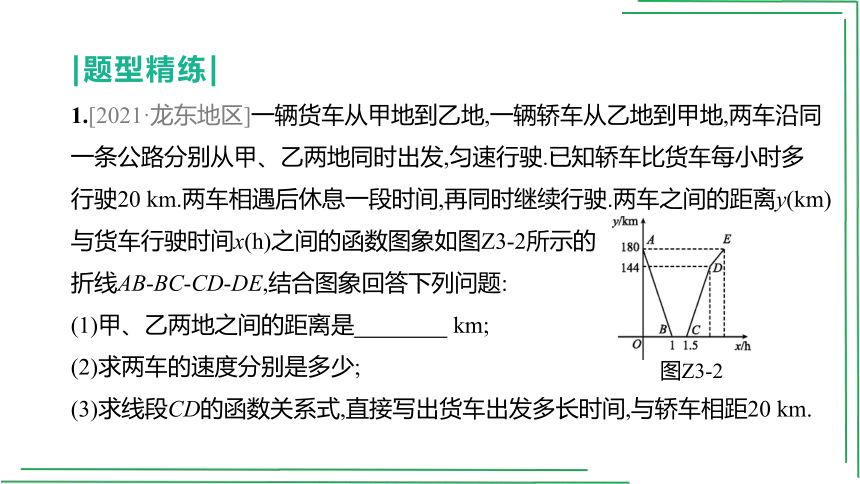
1.[2021·龙东地区]一辆货车从甲地到乙地,一辆轿车从乙地到甲地,两车沿同一条公路分别从甲、乙两地同时出发,匀速行驶.已知轿车比货车每小时多行驶20 km.两车相遇后休息一段时间,再同时继续行驶.两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图Z3-2所示的
折线AB-BC-CD-DE,结合图象回答下列问题:
(1)甲、乙两地之间的距离是 km;
(2)求两车的速度分别是多少;
(3)求线段CD的函数关系式,直接写出货车出发多长时间,与轿车相距20 km.
图Z3-2
(1)甲、乙两地之间的距离是 km;
图Z3-2
180
(2)求两车的速度分别是多少;
解:(2)设货车的速度为m km/h,则轿车的速度为(m+20)km/h,根据题意,得m+(m+20)=180,
解得m=80,m+20=100.
答:货车的速度为80 km/h,轿车的速度为100 km/h.
(3)求线段CD的函数关系式,直接写出货车出发多长时间,与轿车相距20 km.
图Z3-2
(3)设点D的横坐标为x,则:80(x-1.5)+100(x-1.5)=144,解得x=2.3,故点D的坐标为(2.3,144).
设线段CD的函数关系式为y=kx+b(k≠0),则:
解得
∴线段CD的函数关系式为y=180x-270(1.5≤x≤2.3);
货车出发 h或 h,与轿车相距20 km.
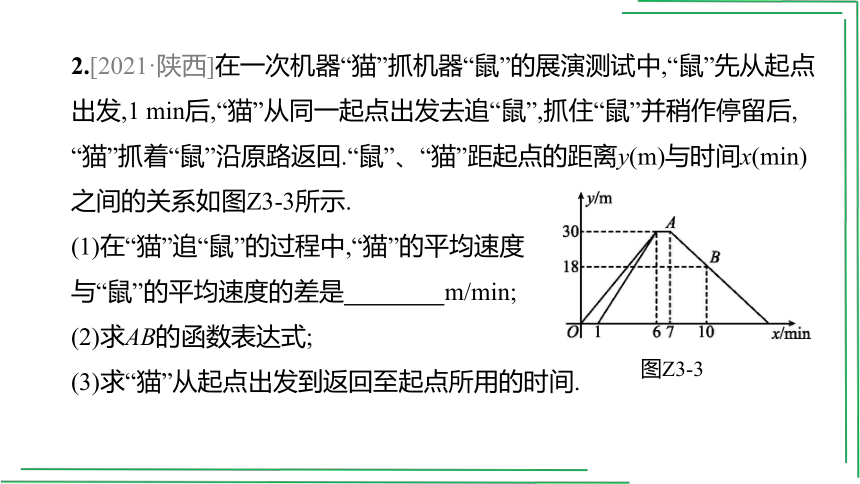
2.[2021·陕西]在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1 min后,“猫”从同一起点出发去追“鼠”,抓住“鼠”并稍作停留后,
“猫”抓着“鼠”沿原路返回.“鼠”、“猫”距起点的距离y(m)与时间x(min)之间的关系如图Z3-3所示.
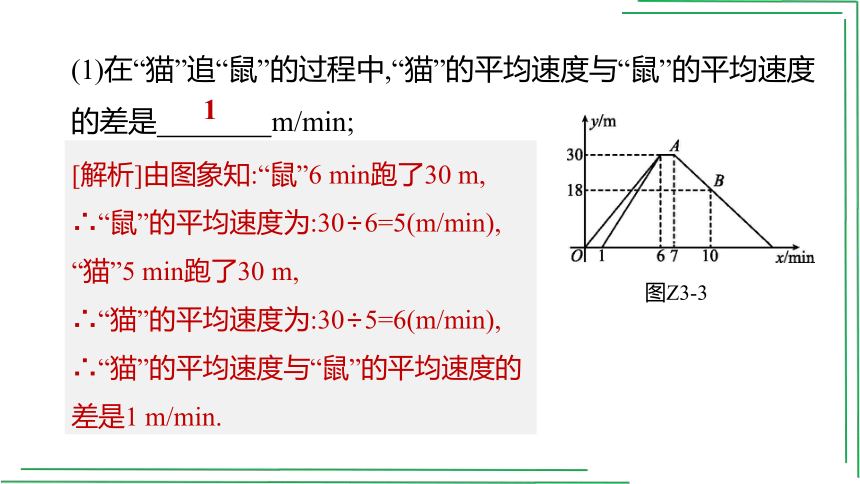
(1)在“猫”追“鼠”的过程中,“猫”的平均速度
与“鼠”的平均速度的差是 m/min;
(2)求AB的函数表达式;
(3)求“猫”从起点出发到返回至起点所用的时间.
图Z3-3
(1)在“猫”追“鼠”的过程中,“猫”的平均速度与“鼠”的平均速度的差是 m/min;
图Z3-3
1
[解析]由图象知:“鼠”6 min跑了30 m,
∴“鼠”的平均速度为:30÷6=5(m/min),
“猫”5 min跑了30 m,
∴“猫”的平均速度为:30÷5=6(m/min),
∴“猫”的平均速度与“鼠”的平均速度的差是1 m/min.
(2)求AB的函数表达式;
图Z3-3
解:(2)设AB的表达式为:y=kx+b(k≠0),
把点A和点B的坐标代入AB的表达式得:
解得:
∴AB的表达式为:y=-4x+58.
(3)求“猫”从起点出发到返回至起点所用的时间.
图Z3-3
(3)令y=0,则-4x+58=0,
∴x=14.5,
∵“猫”比“鼠”迟一分钟出发,
∴“猫”从起点出发到返回至起点所用的时间为14.5-1=13.5(min).
3.[2021·齐齐哈尔]在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车匀速去B地,途经C地时因事停留1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行匀速从B地至A地.甲、乙两人距A地的距离y(米)与时间x(分)之间的函数关系如图Z3-4所示,
请结合图象解答下列问题:
(1)甲的骑行速度为 米/分,
点M的坐标为 ;
图Z3-4
(2)求甲返回时距A地的距离y(米)与时间x(分)之间的函数解析式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回到A地之前, 分钟时两人距C地的距离相等.
图Z3-4
(1)甲的骑行速度为 米/分,点M的坐标为 ;
图Z3-4
240
(6,1200)
[解析]由题意得:甲的骑行速度为:
1020÷(-1)=240(米/分),
240×(11-1)÷2=1200(米),
∵甲往返总时间为11分,中间休息1分钟,
∴M的横坐标为6,则点M的坐标为(6,1200),
故答案为:240,(6,1200).
(2)求甲返回时距A地的距离y(米)与时间x(分)之间的函数解析式(不需要写出自变量的取值范围);
图Z3-4
解:(2)设MN的解析式为y=kx+b(k≠0),
∵y=kx+b(k≠0)的图象过点M(6,1200),N(11,0),
∴解得
∴直线MN的解析式为y=-240x+2640,
即甲返回时距A地的距离y与时间x之间的函数解析式为:
y=-240x+2640.
(3)请直接写出两人出发后,在甲返回到A地之前, 分钟时两人距C地的距离相等.
图Z3-4
4或6或8
[解析]设甲返回A地之前,经过x分两人距C地的距离相等,乙的速度:1200÷20=60(米/分),
如图所示:
∵AB=1200,AC=1020,
∴BC=1200-1020=180.
分5种情况:
①当03,此种情况不符合题意;
②当3∴1020-240x=60x-180,x=4,此种情况符合题意;
③当∴240(x-1)-1020=60x-180,x=6,此种情况不符合题意;
④当x=6时,甲到B地,距离C地180米,乙距C地的距离:6×60-180=180(米),即x=6时两人距C地的距离相等;
⑤当x>6时,甲在返回途中,
当甲在B,C之间时,180-[240(x-1)-1200]=60x-180,x=6,此种情况不符合题意;
当甲在A,C之间时,240(x-1)-1200-180=60x-180,x=8,符合题意.
综上所述,在甲返回A地之前,经过4分钟或6分钟或8分钟时两人距C地的距离相等.
故答案为:4或6或8.
例2 某超市销售一种商品,成本为每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与售价x(元/千克)满足一次函数关系,部分数据如下表:
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),
求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少
类型二
最大利润型问题
售价x(元/千克) 50 60 70
销售量y(千克) 100 80 60
(1)求y与x之间的函数表达式;
售价x(元/千克) 50 60 70
销售量y(千克) 100 80 60
解:(1)设y与x之间的函数表达式为y=kx+b(k≠0),
由题意得解得
∴y与x之间的函数表达式是y=-2x+200.
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
售价x(元/千克) 50 60 70
销售量y(千克) 100 80 60
(2)由题意可得,W=(x-40)(-2x+200)=-2x2+280x-8000,
即W与x之间的函数表达式是W=-2x2+280x-8000.
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少
(3)∵W=-2x2+280x-8000=-2(x-70)2+1800,40≤x≤80,
∴当40≤x≤70时,W随x的增大而增大,当70当x=70时,W取得最大值,此时W最大=1800.
答:当40≤x≤70时,W随x的增大而增大,当70【方法点析】解决利润最值问题,主要分两步,
第一步:列函数关系式,并求得自变量的取值范围.列关系式的依据是“总利润=总售价-总进价=(售价-进价)×销售量”;
第二步:根据解析式求利润最值,如果是一次函数y=kx+b(k≠0),由k的符号确定一次函数的增减性;如果是二次函数,先根据二次项系数确定开口方向(a的符号),再看对称轴是否在自变量取值范围内,或者化为顶点式来确定二次函数的增减性,结合函数图象的增减性求出最值.
|题型精练|
1.[2021·荆门]某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅给出了该商品的售价x,周销售量y,周销售利润W(元)的三组对应数据:
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价为a(元/件),售价x为多少时,周销售利润W最大 并求出此时的最大利润;
(3)因疫情原因,该商品进价提
高了m(元/件)(m>0),公司为回
馈消费者,规定该商品售价x不
得超过55(元/件),且该商品在
今后的销售中,周销售量与售价仍然满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
解:(1)设y=kx+b.由表中数据,得
解得∴y=-3x+300.
(2)若该商品进价为a(元/件),售价x为多少时,周销售利润W最大 并求出此时的最大利润;
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(2)由表格可知3600=180(40-a),解得a=20.
∴W=y(x-a)=(-3x+300)(x-20)=-3x2+360x-6000=-3(x-60)2+4800.
∵-3<0,
∴当x=60时,W最大,最大利润是4800元.
(3)因疫情原因,该商品进价提高了m(元/件)(m>0),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍然满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(3)设周销售利润为W'元,则W'=y(x-a-m)=(-3x+300)(x-20-m)=
-3[x2-(120+m)x+100(20+m)].
∵抛物线的开口向下,对称轴为直线x=>60,且0∴当x=55时,W'最大.
∵W'最大=4050,
∴(-3×55+300)(55-20-m)=4050.
解得m=5.
2.[2021·黄冈]红星公司销售一种成本为40元/件的产品,若月销售单价不高于50元/件,一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售单价不低于成本.设月销售单价为x(单位:元/件),月销售量为y(单位:万件).
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围.
(2)当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元,求a的值.
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围.
解:(1)由题意,当40≤x≤50时,y=5,当x>50时,y=5-0.1(x-50)=
-0.1x+10,
∵y≥0,∴-0.1x+10≥0,解得x≤100.
∴y与x之间的函数关系式为
y=
(2)当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元
(2)设该产品的月销售利润为z万元,
①当40≤x≤50时,z=5(x-40)=5x-200,由一次函数的性质可知,在40≤x≤50内,z随x的增大而增大,∴当x=50时,z取得最大值,z最大=5×50-200=50.
②当50由二次函数的性质知当x=70时,z有最大值为90,
∵90>50,∴当月销售单价是70元/件时,月销售利润最大,最大利润是90万元.
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元,求a的值.
(3)∵捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元(大于50万元),∴50设捐款后当月的销售利润为z'万元.
由题意得z'=(x-40-a)(-0.1x+10),
整理得z'=-0.1×(x-( + )/ )2+ ^ / -3a+90,
∵( + )/ >70,
∴在50∴当x=70时,z'取得最大值,最大值为(70-40-a)(-0.1×70+10)=90-3a,
∴90-3a=78,解得a=4.
∴a的值为4.
3.[2020·南充]某工厂计划在每个生产周期内生产并销售完某型设备,设备的生产成本为10万元/件.
(1)如图Z3-5,设第x(0售价为z万元/件,z与x之间的关系用图中的函
数图象表示,求z关于x的函数解析式(写出x的
范围).
(2)设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0图Z3-5
(1)如图Z3-5,设第x(0图Z3-5
解:(1)由图象可知,当0当12则解得
∴z=-x+19,
∴z关于x的函数解析式为z=
(2)设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0图Z3-5
(2)设第x个生产周期工厂创造的利润为w万元,
①当0∴当x=12时,w最大值=30×12+240=600.
②当12w=(-x+19-10)×(5x+40)
=-x2+35x+360
=-(x-14)2+605,
∴当x=14时,w最大值=605.
综上所述,工厂第14个生产周期创造的利润最大,最大是605万元.
4.[2021·十堰]某商贸公司购进某种商品的成本为20元/kg,经过市场调研发现,这种商品在未来40天的销售单价y(元/kg)与时间x(天)之间的函数关系式为:
y=且日销量m(kg)与时间
x(天)之间的变化规律符合一次函数关系,如下表:
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
(1)填空:m与x的函数关系为 .
(2)哪一天的销售利润最大 最大日销售利润是多少
(3)在实际销售的前20天中,公司决定每销售1 kg商品就捐赠n元利润(n<4)给当地福利院,后发现:在前20天中,每天扣除捐赠后的日销售利润随时间x的增大而增大,求n的取值范围.
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
(1)填空:m与x的函数关系为 .
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
m=-2x+144(1≤x≤40且x为整数)
[解析]由题意可设日销量m(kg)与时间x(天)之间的一次函数关系式为:m=kx+b(k≠0),
将(1,142)和(3,138)代入m=kx+b,有:解得
故m与x的函数关系为:m=-2x+144(1≤x≤40且x为整数).
(2)哪一天的销售利润最大 最大日销售利润是多少
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
(2)设日销售利润为W元,根据题意可得:
当1≤x≤20且x为整数时,W=(0.25x+30-20)(-2x+144)=-0.5x2+16x+
1440=-0.5(x-16)2+1568,
此时当x=16时,取得最大日销售利润,为1568元.
当20此时当x=21时,取得最大日销售利润,最大日销售利润为
-30×21+2160=1530(元),
综上所述,第16天的销售利润最大,最大日销售利润为1568元.
(3)在实际销售的前20天中,公司决定每销售1 kg商品就捐赠n元利润(n<4)给当地福利院,后发现:在前20天中,每天扣除捐赠后的日销售利润随时间x的增大而增大,求n的取值范围.
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
(3)设每天扣除捐赠后的日销售利润为P,根据题意可得:
P=-0.5x2+16x+1440-n(-2x+144)=-0.5x2+(16+2n)x+1440-144n,其对称轴为直线x=16+2n,
∵在前20天中,每天扣除捐赠后的日销售利润随时间x的增大而增大,
∴16+2n≥20,求得n≥2,
又∵n<4,∴n的取值范围是:2≤n<4.
例3 王先生准备在儿童节来临之际向母校捐赠一批(大于100条)某种品牌的跳绳,采购跳绳有在实体店和网店购买两种方式,通过洽谈,获得了以下信息:
类型三
方案抉择问题
购买方式 标价(元/条) 优惠条件
实体店 40 全部按标价的8折出售
网店 40 购买100条或100条以下,按标价出售;购买100条以上,从101条开始按标价的7折出售(免邮寄费)
(1)请分别写出王先生用这两种方式购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式.
(2)王先生选取哪种方式购买跳绳省钱
(3)王先生购买跳绳的预算不超过10000元,他最多能购买多少条跳绳
(1)请分别写出王先生用这两种方式购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式.
购买方式 标价(元/条) 优惠条件
实体店 40 全部按标价的8折出售
网店 40 购买100条或100条以下,按标价出售;购买100条以上,从101条开始按标价的7折出售(免邮寄费)
解:(1)王先生在实体店购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式为y=40x×0.8=32x(x>100且x为整数);
王先生在网店购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式为y=40×100+(x-100)×40×0.7=28x+1200(x>100且x为整数).
(2)王先生选取哪种方式购买跳绳省钱
购买方式 标价(元/条) 优惠条件
实体店 40 全部按标价的8折出售
网店 40 购买100条或100条以下,按标价出售;购买100条以上,从101条开始按标价的7折出售(免邮寄费)
(2)当32x=28x+1200时,解得x=300.
∴当100当x=300时,在实体店和网店购买费用相同;
当x>300时,在网店购买省钱.
(3)王先生购买跳绳的预算不超过10000元,他最多能购买多少条跳绳
购买方式 标价(元/条) 优惠条件
实体店 40 全部按标价的8折出售
网店 40 购买100条或100条以下,按标价出售;购买100条以上,从101条开始按标价的7折出售(免邮寄费)
(3)将y=10000代入y=32x,得x=312.5≈312.
将y=10000代入y=28x+1200,得x≈314.29≈314.
∴王先生最多能购买314条跳绳.
|题型精练|
1.[2021·龙东地区]“中国人的饭碗必须牢牢掌握在咱们自己手中”.为扩大粮食生产规模,某粮食生产基地计划投入-笔资金购进甲、乙两种农机具,已知购进2件甲种农机具和1件乙种农机具共需3.5万元,购进1件甲种农机具和3件乙种农机具共需3万元.
(1)求购进1件甲种农机具和1件乙种农机具各需多少万元;
(2)若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m件,则有哪几种购买方案
(3)在(2)的条件下,哪种购买方案需要的资金最少,最少资金是多少
(1)求购进1件甲种农机具和1件乙种农机具各需多少万元;
解:(1)设购进1件甲种农机具需x万元,购进1件乙种农机具需y万元,
根据题意,得解得
答:购进1件甲种农机具需1.5万元,购进1件乙种农机具需0.5万元.
(2)若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m件,则有哪几种购买方案
(2)由已知得,购进乙种农机具(10-m)件,
根据题意,得9.8≤1.5m+0.5(10-m)≤12,
解得4.8≤m≤7.
∵m为正整数,∴m取5,6,7.
∴有三种购买方案.方案一:购进甲种农机具5件,购进乙种农机具5件;方案二:购进甲种农机具6件,购进乙种农机具4件;方案三:购进甲种农机具7件,购进乙种农机具3件.
(3)在(2)的条件下,哪种购买方案需要的资金最少,最少资金是多少
(3)方案一需要的资金:1.5×5+0.5×5=10(万元);
方案二需要的资金:1.5×6+0.5×4=11(万元);
方案三需要的资金:1.5×7+0.5×3=12(万元).
∴在(2)的条件下,方案一需要的资金最少,最少资金是10万元.
2.[2021·宜昌]甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元/ kg,如果一次购买4 kg以上的苹果,超过4 kg的部分按标价6折售卖.
x(单位: kg)表示购买苹果的质量,y(单位:元)表示付款金额.
(1)文文购买3 kg苹果需付款 元;购买5 kg苹果需付款
元;
(2)求付款金额y关于购买苹果的质量x的函数解析式;
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/ kg,且全部按标价的8折售卖,文文如果要购买10 kg苹果,请问她在哪个超市购买更划算.
(1)文文购买3 kg苹果需付款 元;购买5 kg苹果需付款
元;
30
46
[解析]由题意可知:文文购买3 kg苹果不优惠,∴文文购买3 kg苹果需付款:3×10=30(元),
购买5 kg苹果,4 kg不优惠,1 kg优惠,
∴购买5 kg苹果需付款:4×10+1×10×0.6=46(元),故答案为:30,
46.
(2)求付款金额y关于购买苹果的质量x的函数解析式;
(2)由题意得,当0当x>4时,y=4×10+(x-4)×10×0.6=6x+16,
∴付款金额y关于购买苹果的质量x的函数解析式为:
y=
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/ kg,且全部按标价的8折售卖,文文如果要购买10 kg苹果,请问她在哪个超市购买更划算.
(3)文文在甲超市购买10 kg苹果需付款:6×10+16=76(元),
文文在乙超市购买10 kg苹果需付款:10×10×0.8=80(元),
∵76<80,∴文文在甲超市购买更划算.
3.[2020·襄阳]受新冠疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援.”某水果经销商主动从该种植专业户购进甲,乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果x千克,
付款y元,y与x之间的函数关系如图Z3-6所示.
(1)直接写出当0≤x≤50和x>50时,y与x之间的
函数关系式.
图Z3-6
(2)若经销商计划一次性购进甲,乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲,乙两种水果的购进量,才能使经销商付款总金额w(元)最少
(3)若甲,乙两种水果的销售价格分别为40元/千克
和36元/千克.经销商按(2)中甲,乙两种水果购进量
的分配比例购进两种水果共a千克,且销售完a千
克水果获得的利润不少于1650元,求a的最小值.
图Z3-6
(1)直接写出当0≤x≤50和x>50时,y与x之间的函数关系式.
图Z3-6
解:(1)当0≤x≤50时,设y=k1x,则50k1=1500,解得k1=30;
当x>50时,设y=k2x+b,则
解得
∴y与x之间的函数关系式为
y=
(2)若经销商计划一次性购进甲,乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲,乙两种水果的购进量,才能使经销商付款总金额w(元)最少
(2)由题意知40≤x≤60,下面分两种情况讨论如下:
当40≤x≤50时,w=30x+25(100-x)=5x+2500,易知x=40时,wmin=2700;
当50∵2700<2740,
∴当甲、乙两种水果分别购进40千克,60千克时,经销商付款总金额w(元)最少.
(3)若甲,乙两种水果的销售价格分别为40元/千克和36元/千克.经销商按(2)中甲,乙两种水果购进量的分配比例购进两种水果共a千克,且销售完a千克水果获得的利润不少于1650元,求a的最小值.
(3)由题意可设甲种水果为a千克,乙种水果为a千克.
当0≤a≤50时,即0≤a≤125,则甲种水果的进货价为30元/千克,
(40-30)×a+(36-25)×a≥1650,
解得a≥>125,与0≤a≤125矛盾,故舍去;
当a>50时,即a>125,则a×40-(a×24+300)+a×(36-25)≥1650,解得a≥150,
∴a的最小值为150.
例4 如图Z3-7,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN.已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
类型四
几何图形的面积问题
图Z3-7
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
图Z3-7
解:(1)设AD=m米,则AB=米.依题意,
得·m=450.解得m1=10,m2=90.
因为a=20且m≤a,所以m2=90不合题意,应舍去.
故所利用旧墙AD的长为10米.
(2)求矩形菜园ABCD面积的最大值.
图Z3-7
(2)设AD=x米,矩形ABCD的面积为S平方
米,则0S=·x=-(x2-100x)=-(x-50)2+1250.
①若a≥50,则当x=50时,S最大=1250;
②若0综上,当a≥50时,矩形菜园ABCD的面积的最大值是1250平方米;
当0|题型精练|
1.某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图Z3-8,BE,EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为S平方米.
(1)求出S与x的函数关系式,直接写出自变量x的
取值范围;
(2)若矩形ABCD的面积为252平方米,求AB的长.
图Z3-8
(1)求出S与x的函数关系式,直接写出自变量x的取值范围;
图Z3-8
解:(1)由题意得:BC-1=58-x-x-(x-1),
∴BC=60-3x,
可得矩形ABCD的面积
S=x(60-3x)=-3x2+60x(8≤x<15).
(2)若矩形ABCD的面积为252平方米,求AB的长.
(2)由题意得:S=-3x2+60x=252,
解得:x=14或x=6(舍去),故AB长为14米.
2.如图Z3-9,为美化中心城区环境,政府计划在长(AB)为30米,宽(AD)为20米的矩形场地上修建公园.其中要留出宽度相等的三条小路,且两条与AB平行,另一条与AD平行,其余部分建成花圃.
(1)若花圃总面积为448平方米,求小路宽为多少米.
(2)已知某园林公司修建小路的造价y1(元)和修建
花圃的造价y2(元)与各自的修建面积S1(平方米),
S2(平方米)之间的函数关系分别为y1=40S1和y2=35S2+20000.若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低.
图Z3-9
(1)若花圃总面积为448平方米,求小路宽为多少米.
图Z3-9
解:(1)设小路的宽为m米,则可列
方程(30-m)(20-2m)=448,
解得:m1=2或m2=38(舍去).
答:小路的宽为2米.
(2)已知某园林公司修建小路的造价y1(元)和修建花圃的造价y2(元)与各自的修建面积S1(平方米),S2(平方米)之间的函数关系分别为y1=40S1和y2=35S2+20000.若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低.
图Z3-9
(2)设小路的宽为x米,总造价为w元,
则花圃的面积为(2x2-80x+600)平方米,小路面积为(-2x2+80x)平方米,
∴w=40·(-2x2+80x)+35·(2x2-80x+600)+20000,
整理得:w=-10(x-20)2+45000,
∴当2≤x≤4时,w随x的增大而增大,
∴当x=2时,w取最小值.
答:小路的宽为2米时修建小路和花圃的总造价最低.
例5 [2020·长沙模拟]为构建“魅力雨花,和谐雨花,人文雨花”,规划在圭塘河上修建一座观光人行桥(如图Z3-10),此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的主视图如图②所示,已知桥面上三组拱桥都为相同的抛物线y=-(x-k)2+t的一部分,拱高(抛物线最高点
到桥面的距离)为16米,三条抛
物线依次与桥面AB相交于点A,C,D,B.
类型五
抛物线型问题
图Z3-10
(1)求桥长AB;
(2)已知一组桥拱的造价为a万元,桥面每米的平均造价为b万元.若一组桥拱的造价为整个桥面造价的,这座观光桥的总造价为504万元,求a,b的值.
图Z3-10
(1)求桥长AB;
图Z3-10
解:(1)如图,以线段AC的垂直平分线为y轴,AB所在直线为x轴,建立平面直角坐标系,则抛物线AC的顶点坐标为(0,16),
则y=-x2+16,
当y=0时,解得x1=16,x2=-16,
∴点A的坐标为(-16,0),点C的坐标为(16,0),
∴AC=16-(-16)=16+16=32,
∴AB=3AC=96,即桥长AB为96米.
(2)已知一组桥拱的造价为a万元,桥面每米的平均造价为b万元.若一组桥拱的造价为整个桥面造价的,这座观光桥的总造价为504万元,求a,b的值.
图Z3-10
(2)由题意可得,
解得
答:a的值是72,b的值是3.
|题型精练|
[2020·绍兴、义乌]如图Z3-11①,排球场长为18 m,宽为9 m,网高为2.24 m.队员站在底线O点处发球,球从点O的正上方1.9 m的C点发出,运动路线是抛物线的一部分,当球运动
到最高点A时,高度为2.88 m,即BA=2.88 m,
这时水平距离OB=7 m.以直线OB为x轴,直
线OC为y轴,建立平面直角坐标系,如图②.
图Z3-11
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x的取值范围).并判断这次发球能否过网,是否出界,说明理由.
(2)若球过网后的落点是对方场地①号位内
的点P(如图①,点P距底线1 m,边线0.5 m),
问发球点O在底线上的哪个位置 (参考数
据:取1.4)
图Z3-11
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x的取值范围).并判断这次发球能否过网,是否出界,说明理由.
图Z3-11
解:(1)设抛物线的表达式为y=a(x-7)2+2.88,
将x=0,y=1.9代入上式并解得:a=-0.02,
故抛物线的表达式为y=-0.02(x-7)2+2.88.
当x=9时,y=-0.02×(9-7)2+2.88=2.8>2.24,
当x=18时,y=-0.02×(18-7)2+2.88=0.46>0,
故这次发球过网,但是出界了.
(2)若球过网后的落点是对方场地①号位内的点P(如图①,点P距底线1 m,边线0.5 m),问发球点O在底线上的哪个位置 (参考数据:取1.4)
图Z3-11
(2)如图,分别过点P,O作底线、边线的
平行线PQ,OQ,交于点Q,
在Rt△OPQ中,OQ=18-1=17,
当y=0时,y=-0.02(x-7)2+2.88=0,
解得x1=19,x2=-5(舍去),
∴OP=19,
∴PQ==6≈8.4,
∵9-8.4-0.5=0.1,
∴发球点O在底线上且距右边线0.1 m处.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 03
函数实际应用问题
●方法点析
●题型精练
●题型分类
函数实际应用型问题是把实际生活情境中的数量关系抽象为函数模型(如一次函数、二次函数、反比例函数以及它们的分段函数),进而应用函数知识进行分析、研究、解决的有关问题,求解此类问题的关键是把实际问题中的等量关系转化为两个变量之间的关系,重在考查数学应用意识和建模能力.
例1 [2021·南京]甲、乙两人沿同一直道从A地去B地.甲比乙早1 min出发,乙的速度是甲的2倍.在整个行程中,甲离A地的距离y1(单位:m)与时间x(单位:min)之间的函数关系如图Z3-1所示.
(1)在图Z3-1中画出乙离A地的距离y2(单位:m)与时间x之间的函数图象;
(2)若甲比乙晚5 min到达B地,
求甲整个行程所用的时间.
类型一
行程问题
图Z3-1
(1)在图Z3-1中画出乙离A地的距离y2(单位:m)与时间x之间的函数图象;
解:(1)如图:
图Z3-1
(2)若甲比乙晚5 min到达B地,求甲整个行程所用的时间.
(2)设甲的速度是v m/min,乙整个行程所用的时间为t min,
由题意得:2v·t=(t+1+5)v,解得:t=6,6+1+5=12(min),
答:甲整个行程所用的时间为12 min.
【方法点析】求解此类问题的关键是分析出图中的关键点对应的时间和路程,以及分段函数图象与实际情况的对应关系,进而根据图象中的数据解决问题.
|题型精练|
1.[2021·龙东地区]一辆货车从甲地到乙地,一辆轿车从乙地到甲地,两车沿同一条公路分别从甲、乙两地同时出发,匀速行驶.已知轿车比货车每小时多行驶20 km.两车相遇后休息一段时间,再同时继续行驶.两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图Z3-2所示的
折线AB-BC-CD-DE,结合图象回答下列问题:
(1)甲、乙两地之间的距离是 km;
(2)求两车的速度分别是多少;
(3)求线段CD的函数关系式,直接写出货车出发多长时间,与轿车相距20 km.
图Z3-2
(1)甲、乙两地之间的距离是 km;
图Z3-2
180
(2)求两车的速度分别是多少;
解:(2)设货车的速度为m km/h,则轿车的速度为(m+20)km/h,根据题意,得m+(m+20)=180,
解得m=80,m+20=100.
答:货车的速度为80 km/h,轿车的速度为100 km/h.
(3)求线段CD的函数关系式,直接写出货车出发多长时间,与轿车相距20 km.
图Z3-2
(3)设点D的横坐标为x,则:80(x-1.5)+100(x-1.5)=144,解得x=2.3,故点D的坐标为(2.3,144).
设线段CD的函数关系式为y=kx+b(k≠0),则:
解得
∴线段CD的函数关系式为y=180x-270(1.5≤x≤2.3);
货车出发 h或 h,与轿车相距20 km.
2.[2021·陕西]在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1 min后,“猫”从同一起点出发去追“鼠”,抓住“鼠”并稍作停留后,
“猫”抓着“鼠”沿原路返回.“鼠”、“猫”距起点的距离y(m)与时间x(min)之间的关系如图Z3-3所示.
(1)在“猫”追“鼠”的过程中,“猫”的平均速度
与“鼠”的平均速度的差是 m/min;
(2)求AB的函数表达式;
(3)求“猫”从起点出发到返回至起点所用的时间.
图Z3-3
(1)在“猫”追“鼠”的过程中,“猫”的平均速度与“鼠”的平均速度的差是 m/min;
图Z3-3
1
[解析]由图象知:“鼠”6 min跑了30 m,
∴“鼠”的平均速度为:30÷6=5(m/min),
“猫”5 min跑了30 m,
∴“猫”的平均速度为:30÷5=6(m/min),
∴“猫”的平均速度与“鼠”的平均速度的差是1 m/min.
(2)求AB的函数表达式;
图Z3-3
解:(2)设AB的表达式为:y=kx+b(k≠0),
把点A和点B的坐标代入AB的表达式得:
解得:
∴AB的表达式为:y=-4x+58.
(3)求“猫”从起点出发到返回至起点所用的时间.
图Z3-3
(3)令y=0,则-4x+58=0,
∴x=14.5,
∵“猫”比“鼠”迟一分钟出发,
∴“猫”从起点出发到返回至起点所用的时间为14.5-1=13.5(min).
3.[2021·齐齐哈尔]在一条笔直的公路上依次有A,C,B三地,甲、乙两人同时出发,甲从A地骑自行车匀速去B地,途经C地时因事停留1分钟,继续按原速骑行至B地,甲到达B地后,立即按原路原速返回A地;乙步行匀速从B地至A地.甲、乙两人距A地的距离y(米)与时间x(分)之间的函数关系如图Z3-4所示,
请结合图象解答下列问题:
(1)甲的骑行速度为 米/分,
点M的坐标为 ;
图Z3-4
(2)求甲返回时距A地的距离y(米)与时间x(分)之间的函数解析式(不需要写出自变量的取值范围);
(3)请直接写出两人出发后,在甲返回到A地之前, 分钟时两人距C地的距离相等.
图Z3-4
(1)甲的骑行速度为 米/分,点M的坐标为 ;
图Z3-4
240
(6,1200)
[解析]由题意得:甲的骑行速度为:
1020÷(-1)=240(米/分),
240×(11-1)÷2=1200(米),
∵甲往返总时间为11分,中间休息1分钟,
∴M的横坐标为6,则点M的坐标为(6,1200),
故答案为:240,(6,1200).
(2)求甲返回时距A地的距离y(米)与时间x(分)之间的函数解析式(不需要写出自变量的取值范围);
图Z3-4
解:(2)设MN的解析式为y=kx+b(k≠0),
∵y=kx+b(k≠0)的图象过点M(6,1200),N(11,0),
∴解得
∴直线MN的解析式为y=-240x+2640,
即甲返回时距A地的距离y与时间x之间的函数解析式为:
y=-240x+2640.
(3)请直接写出两人出发后,在甲返回到A地之前, 分钟时两人距C地的距离相等.
图Z3-4
4或6或8
[解析]设甲返回A地之前,经过x分两人距C地的距离相等,乙的速度:1200÷20=60(米/分),
如图所示:
∵AB=1200,AC=1020,
∴BC=1200-1020=180.
分5种情况:
①当0
②当3
③当
④当x=6时,甲到B地,距离C地180米,乙距C地的距离:6×60-180=180(米),即x=6时两人距C地的距离相等;
⑤当x>6时,甲在返回途中,
当甲在B,C之间时,180-[240(x-1)-1200]=60x-180,x=6,此种情况不符合题意;
当甲在A,C之间时,240(x-1)-1200-180=60x-180,x=8,符合题意.
综上所述,在甲返回A地之前,经过4分钟或6分钟或8分钟时两人距C地的距离相等.
故答案为:4或6或8.
例2 某超市销售一种商品,成本为每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与售价x(元/千克)满足一次函数关系,部分数据如下表:
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),
求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少
类型二
最大利润型问题
售价x(元/千克) 50 60 70
销售量y(千克) 100 80 60
(1)求y与x之间的函数表达式;
售价x(元/千克) 50 60 70
销售量y(千克) 100 80 60
解:(1)设y与x之间的函数表达式为y=kx+b(k≠0),
由题意得解得
∴y与x之间的函数表达式是y=-2x+200.
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
售价x(元/千克) 50 60 70
销售量y(千克) 100 80 60
(2)由题意可得,W=(x-40)(-2x+200)=-2x2+280x-8000,
即W与x之间的函数表达式是W=-2x2+280x-8000.
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少
(3)∵W=-2x2+280x-8000=-2(x-70)2+1800,40≤x≤80,
∴当40≤x≤70时,W随x的增大而增大,当70
答:当40≤x≤70时,W随x的增大而增大,当70
第一步:列函数关系式,并求得自变量的取值范围.列关系式的依据是“总利润=总售价-总进价=(售价-进价)×销售量”;
第二步:根据解析式求利润最值,如果是一次函数y=kx+b(k≠0),由k的符号确定一次函数的增减性;如果是二次函数,先根据二次项系数确定开口方向(a的符号),再看对称轴是否在自变量取值范围内,或者化为顶点式来确定二次函数的增减性,结合函数图象的增减性求出最值.
|题型精练|
1.[2021·荆门]某公司电商平台,在2021年五一长假期间,举行了商品打折促销活动,经市场调查发现,某种商品的周销售量y(件)是关于售价x(元/件)的一次函数,下表仅给出了该商品的售价x,周销售量y,周销售利润W(元)的三组对应数据:
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)若该商品进价为a(元/件),售价x为多少时,周销售利润W最大 并求出此时的最大利润;
(3)因疫情原因,该商品进价提
高了m(元/件)(m>0),公司为回
馈消费者,规定该商品售价x不
得超过55(元/件),且该商品在
今后的销售中,周销售量与售价仍然满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
解:(1)设y=kx+b.由表中数据,得
解得∴y=-3x+300.
(2)若该商品进价为a(元/件),售价x为多少时,周销售利润W最大 并求出此时的最大利润;
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(2)由表格可知3600=180(40-a),解得a=20.
∴W=y(x-a)=(-3x+300)(x-20)=-3x2+360x-6000=-3(x-60)2+4800.
∵-3<0,
∴当x=60时,W最大,最大利润是4800元.
(3)因疫情原因,该商品进价提高了m(元/件)(m>0),公司为回馈消费者,规定该商品售价x不得超过55(元/件),且该商品在今后的销售中,周销售量与售价仍然满足(1)中的函数关系,若周销售最大利润是4050元,求m的值.
x 40 70 90
y 180 90 30
W 3600 4500 2100
(注:周销售利润=周销售量×(售价-进价))
(3)设周销售利润为W'元,则W'=y(x-a-m)=(-3x+300)(x-20-m)=
-3[x2-(120+m)x+100(20+m)].
∵抛物线的开口向下,对称轴为直线x=>60,且0
∵W'最大=4050,
∴(-3×55+300)(55-20-m)=4050.
解得m=5.
2.[2021·黄冈]红星公司销售一种成本为40元/件的产品,若月销售单价不高于50元/件,一个月可售出5万件;月销售单价每涨价1元,月销售量就减少0.1万件.其中月销售单价不低于成本.设月销售单价为x(单位:元/件),月销售量为y(单位:万件).
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围.
(2)当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元,求a的值.
(1)直接写出y与x之间的函数关系式,并写出自变量x的取值范围.
解:(1)由题意,当40≤x≤50时,y=5,当x>50时,y=5-0.1(x-50)=
-0.1x+10,
∵y≥0,∴-0.1x+10≥0,解得x≤100.
∴y与x之间的函数关系式为
y=
(2)当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元
(2)设该产品的月销售利润为z万元,
①当40≤x≤50时,z=5(x-40)=5x-200,由一次函数的性质可知,在40≤x≤50内,z随x的增大而增大,∴当x=50时,z取得最大值,z最大=5×50-200=50.
②当50
∵90>50,∴当月销售单价是70元/件时,月销售利润最大,最大利润是90万元.
(3)为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向大别山区捐款a元.已知该公司捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元,求a的值.
(3)∵捐款当月的月销售单价不高于70元/件,月销售最大利润是78万元(大于50万元),∴50
由题意得z'=(x-40-a)(-0.1x+10),
整理得z'=-0.1×(x-( + )/ )2+ ^ / -3a+90,
∵( + )/ >70,
∴在50
∴90-3a=78,解得a=4.
∴a的值为4.
3.[2020·南充]某工厂计划在每个生产周期内生产并销售完某型设备,设备的生产成本为10万元/件.
(1)如图Z3-5,设第x(0
数图象表示,求z关于x的函数解析式(写出x的
范围).
(2)设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0
(1)如图Z3-5,设第x(0
解:(1)由图象可知,当0
∴z=-x+19,
∴z关于x的函数解析式为z=
(2)设第x个生产周期生产并销售的设备为y件,y与x满足关系式y=5x+40(0
(2)设第x个生产周期工厂创造的利润为w万元,
①当0
②当12
=-x2+35x+360
=-(x-14)2+605,
∴当x=14时,w最大值=605.
综上所述,工厂第14个生产周期创造的利润最大,最大是605万元.
4.[2021·十堰]某商贸公司购进某种商品的成本为20元/kg,经过市场调研发现,这种商品在未来40天的销售单价y(元/kg)与时间x(天)之间的函数关系式为:
y=且日销量m(kg)与时间
x(天)之间的变化规律符合一次函数关系,如下表:
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
(1)填空:m与x的函数关系为 .
(2)哪一天的销售利润最大 最大日销售利润是多少
(3)在实际销售的前20天中,公司决定每销售1 kg商品就捐赠n元利润(n<4)给当地福利院,后发现:在前20天中,每天扣除捐赠后的日销售利润随时间x的增大而增大,求n的取值范围.
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
(1)填空:m与x的函数关系为 .
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
m=-2x+144(1≤x≤40且x为整数)
[解析]由题意可设日销量m(kg)与时间x(天)之间的一次函数关系式为:m=kx+b(k≠0),
将(1,142)和(3,138)代入m=kx+b,有:解得
故m与x的函数关系为:m=-2x+144(1≤x≤40且x为整数).
(2)哪一天的销售利润最大 最大日销售利润是多少
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
(2)设日销售利润为W元,根据题意可得:
当1≤x≤20且x为整数时,W=(0.25x+30-20)(-2x+144)=-0.5x2+16x+
1440=-0.5(x-16)2+1568,
此时当x=16时,取得最大日销售利润,为1568元.
当20
-30×21+2160=1530(元),
综上所述,第16天的销售利润最大,最大日销售利润为1568元.
(3)在实际销售的前20天中,公司决定每销售1 kg商品就捐赠n元利润(n<4)给当地福利院,后发现:在前20天中,每天扣除捐赠后的日销售利润随时间x的增大而增大,求n的取值范围.
时间x(天) 1 3 6 10 …
日销m(kg) 142 138 132 124 …
(3)设每天扣除捐赠后的日销售利润为P,根据题意可得:
P=-0.5x2+16x+1440-n(-2x+144)=-0.5x2+(16+2n)x+1440-144n,其对称轴为直线x=16+2n,
∵在前20天中,每天扣除捐赠后的日销售利润随时间x的增大而增大,
∴16+2n≥20,求得n≥2,
又∵n<4,∴n的取值范围是:2≤n<4.
例3 王先生准备在儿童节来临之际向母校捐赠一批(大于100条)某种品牌的跳绳,采购跳绳有在实体店和网店购买两种方式,通过洽谈,获得了以下信息:
类型三
方案抉择问题
购买方式 标价(元/条) 优惠条件
实体店 40 全部按标价的8折出售
网店 40 购买100条或100条以下,按标价出售;购买100条以上,从101条开始按标价的7折出售(免邮寄费)
(1)请分别写出王先生用这两种方式购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式.
(2)王先生选取哪种方式购买跳绳省钱
(3)王先生购买跳绳的预算不超过10000元,他最多能购买多少条跳绳
(1)请分别写出王先生用这两种方式购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式.
购买方式 标价(元/条) 优惠条件
实体店 40 全部按标价的8折出售
网店 40 购买100条或100条以下,按标价出售;购买100条以上,从101条开始按标价的7折出售(免邮寄费)
解:(1)王先生在实体店购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式为y=40x×0.8=32x(x>100且x为整数);
王先生在网店购买跳绳所需的资金y(元)与购买的跳绳数x(条)之间的函数关系式为y=40×100+(x-100)×40×0.7=28x+1200(x>100且x为整数).
(2)王先生选取哪种方式购买跳绳省钱
购买方式 标价(元/条) 优惠条件
实体店 40 全部按标价的8折出售
网店 40 购买100条或100条以下,按标价出售;购买100条以上,从101条开始按标价的7折出售(免邮寄费)
(2)当32x=28x+1200时,解得x=300.
∴当100
当x>300时,在网店购买省钱.
(3)王先生购买跳绳的预算不超过10000元,他最多能购买多少条跳绳
购买方式 标价(元/条) 优惠条件
实体店 40 全部按标价的8折出售
网店 40 购买100条或100条以下,按标价出售;购买100条以上,从101条开始按标价的7折出售(免邮寄费)
(3)将y=10000代入y=32x,得x=312.5≈312.
将y=10000代入y=28x+1200,得x≈314.29≈314.
∴王先生最多能购买314条跳绳.
|题型精练|
1.[2021·龙东地区]“中国人的饭碗必须牢牢掌握在咱们自己手中”.为扩大粮食生产规模,某粮食生产基地计划投入-笔资金购进甲、乙两种农机具,已知购进2件甲种农机具和1件乙种农机具共需3.5万元,购进1件甲种农机具和3件乙种农机具共需3万元.
(1)求购进1件甲种农机具和1件乙种农机具各需多少万元;
(2)若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m件,则有哪几种购买方案
(3)在(2)的条件下,哪种购买方案需要的资金最少,最少资金是多少
(1)求购进1件甲种农机具和1件乙种农机具各需多少万元;
解:(1)设购进1件甲种农机具需x万元,购进1件乙种农机具需y万元,
根据题意,得解得
答:购进1件甲种农机具需1.5万元,购进1件乙种农机具需0.5万元.
(2)若该粮食生产基地计划购进甲、乙两种农机具共10件,且投入资金不少于9.8万元又不超过12万元,设购进甲种农机具m件,则有哪几种购买方案
(2)由已知得,购进乙种农机具(10-m)件,
根据题意,得9.8≤1.5m+0.5(10-m)≤12,
解得4.8≤m≤7.
∵m为正整数,∴m取5,6,7.
∴有三种购买方案.方案一:购进甲种农机具5件,购进乙种农机具5件;方案二:购进甲种农机具6件,购进乙种农机具4件;方案三:购进甲种农机具7件,购进乙种农机具3件.
(3)在(2)的条件下,哪种购买方案需要的资金最少,最少资金是多少
(3)方案一需要的资金:1.5×5+0.5×5=10(万元);
方案二需要的资金:1.5×6+0.5×4=11(万元);
方案三需要的资金:1.5×7+0.5×3=12(万元).
∴在(2)的条件下,方案一需要的资金最少,最少资金是10万元.
2.[2021·宜昌]甲超市在端午节这天进行苹果优惠促销活动,苹果的标价为10元/ kg,如果一次购买4 kg以上的苹果,超过4 kg的部分按标价6折售卖.
x(单位: kg)表示购买苹果的质量,y(单位:元)表示付款金额.
(1)文文购买3 kg苹果需付款 元;购买5 kg苹果需付款
元;
(2)求付款金额y关于购买苹果的质量x的函数解析式;
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/ kg,且全部按标价的8折售卖,文文如果要购买10 kg苹果,请问她在哪个超市购买更划算.
(1)文文购买3 kg苹果需付款 元;购买5 kg苹果需付款
元;
30
46
[解析]由题意可知:文文购买3 kg苹果不优惠,∴文文购买3 kg苹果需付款:3×10=30(元),
购买5 kg苹果,4 kg不优惠,1 kg优惠,
∴购买5 kg苹果需付款:4×10+1×10×0.6=46(元),故答案为:30,
46.
(2)求付款金额y关于购买苹果的质量x的函数解析式;
(2)由题意得,当0
∴付款金额y关于购买苹果的质量x的函数解析式为:
y=
(3)当天,隔壁的乙超市也在进行苹果优惠促销活动,同样的苹果的标价也为10元/ kg,且全部按标价的8折售卖,文文如果要购买10 kg苹果,请问她在哪个超市购买更划算.
(3)文文在甲超市购买10 kg苹果需付款:6×10+16=76(元),
文文在乙超市购买10 kg苹果需付款:10×10×0.8=80(元),
∵76<80,∴文文在甲超市购买更划算.
3.[2020·襄阳]受新冠疫情影响,一水果种植专业户有大量成熟水果无法出售.“一方有难,八方支援.”某水果经销商主动从该种植专业户购进甲,乙两种水果进行销售.专业户为了感谢经销商的援助,对甲种水果的出售价格根据购买量给予优惠,对乙种水果按25元/千克的价格出售.设经销商购进甲种水果x千克,
付款y元,y与x之间的函数关系如图Z3-6所示.
(1)直接写出当0≤x≤50和x>50时,y与x之间的
函数关系式.
图Z3-6
(2)若经销商计划一次性购进甲,乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲,乙两种水果的购进量,才能使经销商付款总金额w(元)最少
(3)若甲,乙两种水果的销售价格分别为40元/千克
和36元/千克.经销商按(2)中甲,乙两种水果购进量
的分配比例购进两种水果共a千克,且销售完a千
克水果获得的利润不少于1650元,求a的最小值.
图Z3-6
(1)直接写出当0≤x≤50和x>50时,y与x之间的函数关系式.
图Z3-6
解:(1)当0≤x≤50时,设y=k1x,则50k1=1500,解得k1=30;
当x>50时,设y=k2x+b,则
解得
∴y与x之间的函数关系式为
y=
(2)若经销商计划一次性购进甲,乙两种水果共100千克,且甲种水果不少于40千克,但又不超过60千克.如何分配甲,乙两种水果的购进量,才能使经销商付款总金额w(元)最少
(2)由题意知40≤x≤60,下面分两种情况讨论如下:
当40≤x≤50时,w=30x+25(100-x)=5x+2500,易知x=40时,wmin=2700;
当50
∴当甲、乙两种水果分别购进40千克,60千克时,经销商付款总金额w(元)最少.
(3)若甲,乙两种水果的销售价格分别为40元/千克和36元/千克.经销商按(2)中甲,乙两种水果购进量的分配比例购进两种水果共a千克,且销售完a千克水果获得的利润不少于1650元,求a的最小值.
(3)由题意可设甲种水果为a千克,乙种水果为a千克.
当0≤a≤50时,即0≤a≤125,则甲种水果的进货价为30元/千克,
(40-30)×a+(36-25)×a≥1650,
解得a≥>125,与0≤a≤125矛盾,故舍去;
当a>50时,即a>125,则a×40-(a×24+300)+a×(36-25)≥1650,解得a≥150,
∴a的最小值为150.
例4 如图Z3-7,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN.已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.
类型四
几何图形的面积问题
图Z3-7
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
图Z3-7
解:(1)设AD=m米,则AB=米.依题意,
得·m=450.解得m1=10,m2=90.
因为a=20且m≤a,所以m2=90不合题意,应舍去.
故所利用旧墙AD的长为10米.
(2)求矩形菜园ABCD面积的最大值.
图Z3-7
(2)设AD=x米,矩形ABCD的面积为S平方
米,则0
①若a≥50,则当x=50时,S最大=1250;
②若0
当0
1.某养鸡专业户用篱笆及一面墙(该墙可用最大长度为36米)围成一个矩形场地ABCD来供鸡室外活动,该场地中间隔有一道与AB平行的篱笆(EF),如图Z3-8,BE,EF上各留有1米宽的门(门不需要篱笆),该养鸡专业户共用篱笆58米,设该矩形的一边AB长x米,AD>AB,矩形ABCD的面积为S平方米.
(1)求出S与x的函数关系式,直接写出自变量x的
取值范围;
(2)若矩形ABCD的面积为252平方米,求AB的长.
图Z3-8
(1)求出S与x的函数关系式,直接写出自变量x的取值范围;
图Z3-8
解:(1)由题意得:BC-1=58-x-x-(x-1),
∴BC=60-3x,
可得矩形ABCD的面积
S=x(60-3x)=-3x2+60x(8≤x<15).
(2)若矩形ABCD的面积为252平方米,求AB的长.
(2)由题意得:S=-3x2+60x=252,
解得:x=14或x=6(舍去),故AB长为14米.
2.如图Z3-9,为美化中心城区环境,政府计划在长(AB)为30米,宽(AD)为20米的矩形场地上修建公园.其中要留出宽度相等的三条小路,且两条与AB平行,另一条与AD平行,其余部分建成花圃.
(1)若花圃总面积为448平方米,求小路宽为多少米.
(2)已知某园林公司修建小路的造价y1(元)和修建
花圃的造价y2(元)与各自的修建面积S1(平方米),
S2(平方米)之间的函数关系分别为y1=40S1和y2=35S2+20000.若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低.
图Z3-9
(1)若花圃总面积为448平方米,求小路宽为多少米.
图Z3-9
解:(1)设小路的宽为m米,则可列
方程(30-m)(20-2m)=448,
解得:m1=2或m2=38(舍去).
答:小路的宽为2米.
(2)已知某园林公司修建小路的造价y1(元)和修建花圃的造价y2(元)与各自的修建面积S1(平方米),S2(平方米)之间的函数关系分别为y1=40S1和y2=35S2+20000.若要求小路宽度不少于2米且不超过4米,求小路宽为多少米时修建小路和花圃的总造价最低.
图Z3-9
(2)设小路的宽为x米,总造价为w元,
则花圃的面积为(2x2-80x+600)平方米,小路面积为(-2x2+80x)平方米,
∴w=40·(-2x2+80x)+35·(2x2-80x+600)+20000,
整理得:w=-10(x-20)2+45000,
∴当2≤x≤4时,w随x的增大而增大,
∴当x=2时,w取最小值.
答:小路的宽为2米时修建小路和花圃的总造价最低.
例5 [2020·长沙模拟]为构建“魅力雨花,和谐雨花,人文雨花”,规划在圭塘河上修建一座观光人行桥(如图Z3-10),此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的主视图如图②所示,已知桥面上三组拱桥都为相同的抛物线y=-(x-k)2+t的一部分,拱高(抛物线最高点
到桥面的距离)为16米,三条抛
物线依次与桥面AB相交于点A,C,D,B.
类型五
抛物线型问题
图Z3-10
(1)求桥长AB;
(2)已知一组桥拱的造价为a万元,桥面每米的平均造价为b万元.若一组桥拱的造价为整个桥面造价的,这座观光桥的总造价为504万元,求a,b的值.
图Z3-10
(1)求桥长AB;
图Z3-10
解:(1)如图,以线段AC的垂直平分线为y轴,AB所在直线为x轴,建立平面直角坐标系,则抛物线AC的顶点坐标为(0,16),
则y=-x2+16,
当y=0时,解得x1=16,x2=-16,
∴点A的坐标为(-16,0),点C的坐标为(16,0),
∴AC=16-(-16)=16+16=32,
∴AB=3AC=96,即桥长AB为96米.
(2)已知一组桥拱的造价为a万元,桥面每米的平均造价为b万元.若一组桥拱的造价为整个桥面造价的,这座观光桥的总造价为504万元,求a,b的值.
图Z3-10
(2)由题意可得,
解得
答:a的值是72,b的值是3.
|题型精练|
[2020·绍兴、义乌]如图Z3-11①,排球场长为18 m,宽为9 m,网高为2.24 m.队员站在底线O点处发球,球从点O的正上方1.9 m的C点发出,运动路线是抛物线的一部分,当球运动
到最高点A时,高度为2.88 m,即BA=2.88 m,
这时水平距离OB=7 m.以直线OB为x轴,直
线OC为y轴,建立平面直角坐标系,如图②.
图Z3-11
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x的取值范围).并判断这次发球能否过网,是否出界,说明理由.
(2)若球过网后的落点是对方场地①号位内
的点P(如图①,点P距底线1 m,边线0.5 m),
问发球点O在底线上的哪个位置 (参考数
据:取1.4)
图Z3-11
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x的取值范围).并判断这次发球能否过网,是否出界,说明理由.
图Z3-11
解:(1)设抛物线的表达式为y=a(x-7)2+2.88,
将x=0,y=1.9代入上式并解得:a=-0.02,
故抛物线的表达式为y=-0.02(x-7)2+2.88.
当x=9时,y=-0.02×(9-7)2+2.88=2.8>2.24,
当x=18时,y=-0.02×(18-7)2+2.88=0.46>0,
故这次发球过网,但是出界了.
(2)若球过网后的落点是对方场地①号位内的点P(如图①,点P距底线1 m,边线0.5 m),问发球点O在底线上的哪个位置 (参考数据:取1.4)
图Z3-11
(2)如图,分别过点P,O作底线、边线的
平行线PQ,OQ,交于点Q,
在Rt△OPQ中,OQ=18-1=17,
当y=0时,y=-0.02(x-7)2+2.88=0,
解得x1=19,x2=-5(舍去),
∴OP=19,
∴PQ==6≈8.4,
∵9-8.4-0.5=0.1,
∴发球点O在底线上且距右边线0.1 m处.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
