2022中考数学三轮冲刺专题突破04 阅读理解型题 课件(共71张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺专题突破04 阅读理解型题 课件(共71张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 08:45:38 | ||
图片预览











文档简介
(共71张PPT)
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 04
阅读理解型题
求解新定义运算问题的关键是弄清新定义中的运算法则,并能将其转化为数与式的运算、方程与方程组、不等式与不等式组等问题.
类型一
新定义运算型阅读题
B
2.[2021·包头]定义新运算“ ”,规定:a b=a-2b.若关于x的不等式x m>3的解集为x>-1,则m的值是 ( )
A.-1 B.-2 C.1 D.2
B
[解析] ∵a b=a-2b,x m>3,∴x-2m>3,∴x>2m+3.
又∵x m>3的解集为x>-1,∴2m+3=-1,解得m=-2.
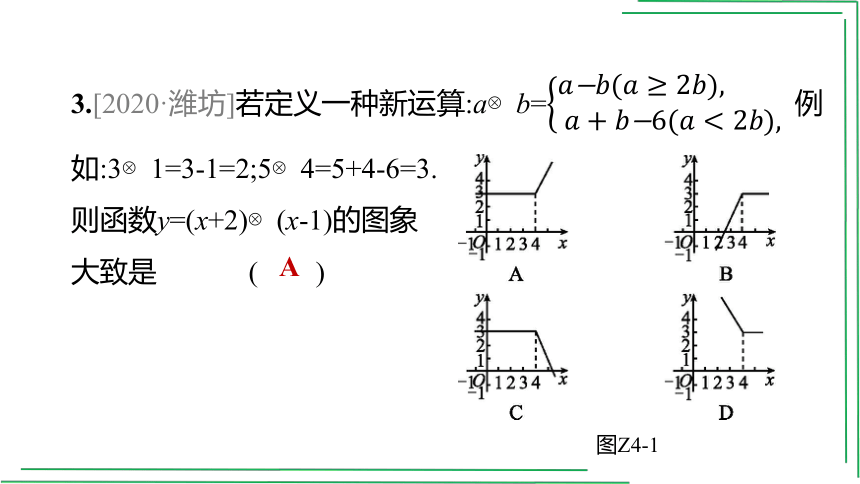
3.[2020·潍坊]若定义一种新运算:a b=例如:3 1=3-1=2;5 4=5+4-6=3.
则函数y=(x+2) (x-1)的图象
大致是 ( )
图Z4-1
A
[解析]根据a b=可分两种情况:当x≤4时,
(x+2) (x-1)=(x+2)-(x-1)=x+2-x+1=3,即:y=3;
当x>4时,(x+2) (x-1)=(x+2)+(x-1)-6=x+2+x-1-6=2x-5,
即:y=2x-5,A选项符合题意,故选A.
4.四则运算符号有+,-,×,÷,现引入两个新运算符号∨,∧,合称“六则运算”.a∨b的运算结果是a和b中较大的数,a∧b的运算结果是a和b中较小的数.下列等式不一定成立的是 ( )
A.(a∨b)+(a∧b)=a+b
B.(-a)∨(-b)=-(a∧b)
C.(a∨b)×c=(ac)∨(bc)
D.a-(b∨c)=(a-b)∧(a-c)
C
5.[2019·德州]已知:[x]表示不超过x的最大整数.例:[4.8]=4,
[-0.8]=-1.现定义:{x}=x-[x],例:{1.5}=1.5-[1.5]=0.5,则{3.9}+
{-1.8}-{1}= .
1.1
[解析]根据题意可得:{3.9}+{-1.8}-{1}=3.9-3-1.8+2-1+1=1.1,故答案为:1.1.
6.[2020·通辽]用※定义一种新运算:对于任意实数m和n,规定m※n=m2n-mn-3n,
如:1※2=12×2-1×2-3×2=-6.
(1)求(-2)※;
(2)若3※m≥-6,求m的取值范围,并在所给的数轴上表示出解集.
图Z4-2
解:(1)(-2)※=(-2)2×-(-2)×-3×=4+2-3=3.
(2)∵3※m=32m-3m-3m=3m,3※m≥-6,∴3m≥-6,得m≥-2.
在数轴上表示如下:
7.[2020·张家界]阅读下面材料:
对于实数a,b,我们定义符号min{a,b}的意义为:当amin{5,5}=5.
根据上面的材料回答下列问题:
(1)min{-1,3}= ;
(2)当min时,求x的取值范围.
-1
(2)当min时,求x的取值范围.
(2)由题意得:≥,3(2x-3)≥2(x+2),6x-9≥2x+4,4x≥13,x≥,
∴x的取值范围为x≥.
求解新定义几何概念型问题的关键是弄清新概念的本质,将其与已学过的数学知识建立联系,并应用相关知识解决问题.
类型二
新定义几何概念型阅读题
1.如图Z4-3,若△ABC内一点P满足∠PAC
=∠PCB=∠PBA,则称点P为△ABC的
“布罗卡尔点”.三角形的布罗卡尔点
是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,“布罗卡尔点”的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,
∠ACB=120°,P为△ABC的“布罗卡尔点”,若PA=,则PB+PC=
.
图Z4-3
1+
[解析]如图,由“布罗卡尔点”的定义,设∠PAC=∠PCB=∠PBA=α,
又CA=CB,∠ACB=120°,
∴∠ABC=∠BAC=30°,∴∠CBP=∠PAB=30°-α=β,
∴△BCP∽△ABP,∴.
在△ABC中,作CD⊥AB于D,则BD=AB,
而cos∠ABC=,∴,∴,
∴PB=1,PC=,∴PB+PC=1+.
2.[2020·怀化]定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 .(填序号)
①平行四边形;②矩形;③菱形;④正方形.
(2)图形判定:如图Z4-4①,在四边形ABCD
中,AD∥BC,AC⊥BD,过点D作BD的垂线
交BC的延长线于点E,且∠DBC=45°,证明:四边形ABCD是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图②中,面积为24的垂等四边形ABCD内接于☉O中,
∠BCD=60°.求☉O的半径.
图Z4-4
(1)下面四边形是垂等四边形的是 .(填序号)
①平行四边形;②矩形;③菱形;④正方形.
④
[解析]①平行四边形的对角线互相平分但不垂直和相等,故不是垂等四边形;
②矩形对角线相等但不垂直,故不是垂等四边形;
③菱形的对角线互相垂直但不相等,故不是垂等四边形;
④正方形的对角线互相垂直且相等,故正方形是垂等四边形.
故选④.
(2)图形判定:如图Z4-4①,在四边形ABCD中,AD∥BC,AC⊥BD,过点D作BD的垂线交BC的延长线于点E,且∠DBC=45°,证明:四边形ABCD是垂等四边形.
图Z4-4
解:(2)证明:∵AC⊥BD,ED⊥BD,∴AC∥DE,
又∵AD∥BC,
∴四边形ADEC是平行四边形,∴AC=DE.
∵BD⊥DE,∠DBC=45°,
∴△BDE是等腰直角三角形,∴BD=DE,∴BD=AC,
又∵BD⊥AC,∴四边形ABCD是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图②中,面积为24的垂等四边形ABCD内接于☉O中,∠BCD=60°.求☉O的半径.
图Z4-4
(3)如图,过点O作OE⊥BD于点E,连接OD,
∵四边形ABCD是垂等四边形,
∴AC=BD,
又∵垂等四边形ABCD的面积是24,
∴AC·BD=24,解得AC=BD=4,
又∵∠BCD=60°,∴∠DOE=60°,
设半径为r,根据垂径定理可得:
在Rt△ODE中,OD=r,DE=2,
∴r==4,
∴☉O的半径为4.
3.[2021·枣庄]如图Z4-5①,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图②,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗 请说明理由.
(2)性质探究:如图①,垂美四边
形ABCD的对角线AC,BD交于
点O.猜想:AB2+CD2与AD2+BC2有什么关系 并证明你的猜想.
(3)解决问题:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE.已知AC=4,AB=5,求GE的长.
图Z4-5
(1)概念理解:如图②,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗 请说明理由.
图Z4-5
解:(1)四边形ABCD是垂美四边形.
理由:连接AC,BD,
∵AB=AD,∴点A在线段BD的垂直平分线上,
∵CB=CD,∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形.
(2)性质探究:如图①,垂美四边形ABCD的对角线AC,BD交于点O.猜想:AB2+CD2与AD2+BC2有什么关系 并证明你的猜想.
图Z4-5
(2)AD2+BC2=AB2+CD2.
证明:∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2.
(3)解决问题:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,
连接CE,BG,GE.已知AC=4,AB=5,求GE的长.
图Z4-5
(3)如图,连接CG,BE.
∵四边形ACFG和四边形ABDE是正方形,
∴AG=AC,AE=AB,∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,
即∠GAB=∠CAE,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC.
设CE交AB于点M,
∵∠AEC+∠AME=90°,∠CMB=∠AME,
∴∠ABG+∠CMB=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=3,CG=4,BE=5,
∴GE2=CG2+BE2-CB2=73,
∵GE>0,∴GE=.
新方法型阅读题指材料中先给出一种新的解题方法,通过阅读体会新方法的实质,然后用新方法解决相关问题.
类型三
新方法型阅读题
1.[2020·常德]阅读理解:对于x3-(n2+1)x+n这类特殊的代数式可以按下面的方法分解因式:
x3-(n2+1)x+n=x3-n2x-x+n=x(x2-n2)-(x-n)=x(x-n)(x+n)-(x-n)=(x-n)
(x2+nx-1).
理解运用:如果x3-(n2+1)x+n=0,那么(x-n)(x2+nx-1)=0,即有x-n=0或x2+nx-1=0,因此,方程x-n=0和x2+nx-1=0的所有解就是方程
x3-(n2+1)x+n=0的解.
解决问题:方程x3-5x+2=0的解为 .
2或-1+或-1-
[解析]∵x3-5x+2=0,
∴x3-4x-x+2=0,∴x(x2-4)-(x-2)=0,
∴x(x+2)(x-2)-(x-2)=0,
则(x-2)[x(x+2)-1]=0,即(x-2)(x2+2x-1)=0,
∴x-2=0或x2+2x-1=0,解得x=2或x=-1±,故答案为2或-1+或-1-.
2.[2020·呼和浩特]“通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程x-=0,就可以利用该思维方式,设=y,将原方程转化为:y2-y=0这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.
已知实数x,y满足求x2+y2的值.
解:令xy=a,x+y=b,则原方程组可化为:
整理得:
②-①得:11a2=275,
解得:a2=25,代入②可得:b=4,
∴方程组的解为:或
x2+y2=(x+y)2-2xy=b2-2a,
当a=5时,x2+y2=6,
当a=-5时,x2+y2=26,
因此x2+y2的值为6或26.
3.[2021·遂宁]已知平面直角坐标系中,点P(x0,y0)和直线Ax+By+C=0(其中A,B不全为0),则点P到直线Ax+By+C=0的距离d可用公式d=来计算.
例如:求点P(1,2)到直线y=2x+1的距离,因为直线y=2x+1可化为2x-y+1=0,其中A=2,B=-1,C=1,所以点P(1,2)到直线y=2x+1的距离为:
d=.
根据以上材料,解答下列问题:
(1)求点M(0,3)到直线y=x+9的距离;
(2)在(1)的条件下,☉M的半径r=4,判断☉M与直线y=x+9的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.
解:(1)∵y=x+9可变形为x-y+9=0,
则其中A=,B=-1,C=9,
由公式得,点M(0,3)到直线y=x+9的距离d==3,
∴点M到直线y=x+9的距离为3.
(2)在(1)的条件下,☉M的半径r=4,判断☉M与直线y=x+9的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.
(2)如图,由(1)可知:圆心到直线的距离d=3,
∵圆的半径r=4,∴d∴直线y=x+9与☉M相交,两交点记作E,F,
连接EM,过点M作MH⊥EF于H,则EF=2EH,
在Rt△EHM中,EM=4,MH=3,
根据勾股定理得,EH=,
∴弦长n=EF=2EH=2.
4.[2021·鄂州]数学课外活动小组的同学在学习了完全平方公式之后,针对两个正数之和与这两个正数之积的算术平方根的两倍之间的关系进行了探究,请阅读以下探究过程并解决问题.
猜想发现
由5+5=2=10;=2;0.4+0.4=2=0.8;
+5>2=2;0.2+3.2>2=1.6;>2.
猜想:如果a>0,b>0,那么存在a+b≥2(当且仅当a=b时等号成立).
猜想证明
∵()2≥0,∴①当且仅当=0,即a=b时,a-2+b
=0,∴a+b=2;
②当≠0,即a≠b时,a-2+b>0,∴a+b>2.
综合上述可得:若a>0,b>0,则a+b≥2成立(当且仅当a=b时等号成立).
猜想运用
对于函数y=x+(x>0),当x取何值时,函数y的值最小 最小值是多少
变式探究
对于函数y=+x(x>3),当x取何值时,函数y的值最小 最小值是多少
拓展应用
疫情期间,为了解决疑似人员的临时隔离问题,高速公路检测站入口处,检测人员利用检测站的一面墙(墙的长度不限),用63米长的钢丝网围成了9间相同的长方形隔离房,如图Z4-6.设每间隔离房的面积为S(米2).问:每间隔离房的长、宽各为多少时,可使每间隔离房的面积S最大 最大面积是多少
图Z4-6
猜想运用
对于函数y=x+(x>0),当x取何值时,函数y的值最小 最小值是多少
解:猜想运用
∵x>0,∴>0,∴y=x+≥2=2,
∴当x=时,ymin=2.此时x2=1,
∵x>0,
∴x=1,即x=1时,函数y的值最小,最小值为2.
变式探究
对于函数y=+x(x>3),当x取何值时,函数y的值最小 最小值是多
少
变式探究
∵x>3,∴x-3>0,>0,∴y=+x-3+3≥2+3=5,
∴当=x-3时,ymin=5,
此时(x-3)2=1,∴x1=4,x2=2(舍去),
即x=4时,函数y的值最小,最小值为5.
拓展应用
疫情期间,为了解决疑似人员的临时隔离问题,高速公路检测站入口处,检测人员利用检测站的一面墙(墙的长度不限),用63米长的钢丝网围成了9间相同的长方形隔离房,如图Z4-6.设每间隔离房的面积为S(米2).问:每间隔离房的长、宽各为多少时,可使每间隔离房的面积S最大 最大面积是多少
图Z4-6
拓展应用
设每间隔离房与墙平行的边为x米,与墙垂直的边为y米,依题意得:
9x+12y=63,即3x+4y=21.
∵3x>0,4y>0,∴3x+4y≥2,
即21≥2,整理得xy≤,即S≤,
∴当3x=4y时,Smax=,此时x=,y=,
即每间隔离房长为米,宽为米时,S的最大值为米2.
5.阅读下面材料:
某同学遇到这样一个问题:如图Z4-7①,△ABC中,AB=AC,点D在BC边上,过点B作BE⊥AD交AD延长线于点E,当BC=2AE时,图①中是否存在与AD相等的线段 若存在,请找出并说明理由;若不存在,说明理由.该同学通过探究发现,过点A作BC的垂线AF,垂足为F,能得到一对全等三角
形(如图②),从而将问题解决.
请回答:
图Z4-7
(1)该同学发现的与AD相等的线段是 .
(2)证明该同学所发现的结论.
参考该同学思考问题的方法,解决下面的问题:
(3)如图③,在△ABC中,AB=AC,∠BAC=90°,点D在BC上,点E是△ABC外一点,且AE=AD,∠DAE=45°,点F是BC中点,G在AB上,连接EF,DG,
∠EFC+∠AGD=90°,
求的值.
图Z4-7
BD
(2)证明该同学所发现的结论.
图Z4-7
解:(2)证明:∵△ABC是等腰三角形,
AF⊥BC,∴BC=2BF.
∵BC=2AE,∴BF=AE.
在Rt△ABF和Rt△BAE中,
∴Rt△ABF≌Rt△BAE(HL),
∴∠BAE=∠ABF,∴BD=AD.
参考该同学思考问题的方法,解决下面的问题:
(3)如图③,在△ABC中,AB=AC,∠BAC=90°,点D在BC上,点E是△ABC外一点,且AE=AD,∠DAE=45°,点F是BC中点,G在AB上,连接EF,DG,∠EFC+∠AGD=90°,求的值.
图Z4-7
(3)如图,连接AF,
∵AB=AC,∠BAC=90°,点F是BC中点,
∴AF⊥BC,∠BAF=∠BAC=45°,AF=BC,∴∠EFC+∠AFE=90°,
∵∠EFC+∠AGD=90°,∴∠AFE=∠AGD,
∵∠DAE=45°,∴∠BAF=∠DAE,
∴∠BAF+∠FAD=∠DAE+∠FAD,即∠GAD=∠FAE.
在△AGD和△AFE中,
∴△AGD≌△AFE,∴AG=AF.
∵AF=BC,∴AG=BC,∴.
1.[2021·襄阳]在△ABC中,∠ACB=90°,=m,D是边BC上一点,将△ABD沿AD折叠得到△AED,连接BE.
(1)特例发现 如图Z4-8①,当m=1,AE落在直线AC上时.
①求证:∠DAC=∠EBC;
②填空:的值为 ;
类型四
类比探究型阅读题
图Z4-8
(2)类比探究 如图②,当m≠1,AE与边BC相交时,在AD上取一点G,使∠ACG=∠BCE,CG交AE于点H,探究的值(用含m的式子表示),并写出探究过程;
(3)拓展运用 在(2)的条件下,当m=,
D是BC的中点时,若EB·EH=6,求CG的长.
图Z4-8
(1)特例发现 如图Z4-8①,当m=1,AE落在直线AC上时.
①求证:∠DAC=∠EBC;
图Z4-8
解:(1)①证明:方法一:当m=1,AE落在直线AC
上时,有AC=BC,而∠ACB=90°,于是
∠ABC=∠CAB=45°;
而由折叠知AB=AE,∠BAD=∠EAD=22.5°.
∵AB=AE,∠CAB=45°,
∴∠ABE=∠AEB==67.5°.
∴∠EBC=∠ABE-∠ABC=67.5°-45°=22.5°.∴∠DAC=∠EBC.
方法二:如图①,延长AD交BE于点F,则由折叠知AF⊥BE于点F,于是∠BFD=∠ACD=90°.
又∠BDF=∠ADC,
故∠DAC=∠EBC.
(1)特例发现 如图Z4-8①,当m=1,AE落在直线AC上时.
②填空:的值为 ;
图Z4-8
1
(2)类比探究 如图②,当m≠1,AE与边BC相交时,在AD上取一点G,使∠ACG=∠BCE,CG交AE于点H,探究的值(用含m的式子表示),并写出探究过程;
图Z4-8
(2)如图②,延长AD交BE于点F,由(1)①可知∠DAC=∠EBC.
又∵∠ACG=∠BCE,
∴△ACG∽△BCE.∴=m.
(3)拓展运用 在(2)的条件下,当m=,D是BC的中点时,若EB·EH=6,求CG的长.
图Z4-8
(3)如图②,由折叠知BF=EF,∠AFB=90°,
又∵D是BC的中点,∴DF∥CE.
∴∠BEC=∠BFA=90°,
∠GAH=∠CEH.
由(2)知△ACG∽△BCE,
从而∠AGC=∠BEC=90°,=m=.
∴,∴=tan∠GAC=.
设CG=x,则CE=x,AG=x,BE=2x,∴AG=CE.
又∵∠AHG=∠EHC,∴△AGH≌△ECH.
∴CH=GH,AH=EH,∴GH=x.
在Rt△AGH中,由勾股定理,得AH=x.
∵EB·EH=6,∴2x·x=6,∴x=±(负值舍去),∴CG=.
2.[2021·达州]某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
【观察与猜想】
(1)如图Z4-9①,在正方形ABCD中,
点E,F分别是AB,AD上的两点,连接
DE,CF,DE⊥CF,则的值为 ;
(2)如图②,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接
CE,BD,且CE⊥BD,则的值为 ;
图Z4-9
【类比探究】
(3)如图③,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE·AB=CF·AD;
图Z4-9
【拓展延伸】
(4)如图④,在Rt△ABD中,∠BAD=90°,AD=9,tan∠ADB=,将
△ABD沿BD翻折,点A落在点C处得△CBD,点E,F分别在边AB,AD上,连接DE,CF,DE⊥CF.
①求的值;
②连接BF,若AE=1,直接写出BF的长度.
图Z4-9
【观察与猜想】
(1)如图Z4-9①,在正方形ABCD
中,点E,F分别是AB,AD上的两点,
连接DE,CF,DE⊥CF,则的值为
;
图Z4-9
1
[解析]如图①,设DE与CF交于点G,
∵四边形ABCD是正方形,
∴∠A=∠FDC=90°,AD=CD,
∵DE⊥CF,∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,∴∠CFD=∠AED,
在△AED和△DFC中,
∴△AED≌△DFC(AAS),∴DE=CF,∴=1.
【观察与猜想】
(2)如图②,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE,BD,且CE⊥BD,则的值为 ;
图Z4-9
[解析]如图②,设DB与CE交于点G,
∵四边形ABCD是矩形,∴∠A=∠EDC=90°.
∵CE⊥BD,∴∠DGC=90°,
∴∠CDG+∠ECD=90°,∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,∴△DEC∽△ABD,∴.
【类比探究】
(3)如图③,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE·AB=CF·AD;
图Z4-9
(3)证明:如图③,过点C作CH⊥AF交AF的延长线于点H,
∵CG⊥EG,∴∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∵∠DFG=∠CFH,∴∠FCH=∠FDG,
∵∠ADE=∠FDG,∴∠FCH=∠ADE,
∵∠A=∠H,
∴△DEA∽△CFH,∴,∴,
∴DE·AB=CF·AD.
【拓展延伸】
(4)如图④,在Rt△ABD中,∠BAD=90°,AD=9,tan∠ADB=,将
△ABD沿BD翻折,点A落在点C处得△CBD,点E,F分别在边AB,AD上,连接DE,CF,DE⊥CF.
①求的值;
②连接BF,若AE=1,直接写出BF的长度.
图Z4-9
(4)①如图④,过点C作CG⊥AD于点G,连接AC交BD于点H,CG与DE相交于点O,则CH⊥BD.
∵CG⊥AD,CF⊥DE,
∴∠FCG+∠CFG=∠CFG+∠ADE=90°,
∴∠FCG=∠ADE,∠BAD=∠CGF=90°,
∴△DEA∽△CFG,∴.
在Rt△ABD中,tan∠ADB=,AD=9,∴AB=3,
在Rt△ADH中,tan∠ADH=,∴,
设AH=a,则DH=3a,
∵AH2+DH2=AD2,∴a2+(3a)2=92,
∴a=(负值已舍去),
∴AH=,DH=,
∴AC=2AH=.
∵S△ADC=AC·DH=AD·CG,
∴×9CG,
∴CG=,∴.
②BF=.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 04
阅读理解型题
求解新定义运算问题的关键是弄清新定义中的运算法则,并能将其转化为数与式的运算、方程与方程组、不等式与不等式组等问题.
类型一
新定义运算型阅读题
B
2.[2021·包头]定义新运算“ ”,规定:a b=a-2b.若关于x的不等式x m>3的解集为x>-1,则m的值是 ( )
A.-1 B.-2 C.1 D.2
B
[解析] ∵a b=a-2b,x m>3,∴x-2m>3,∴x>2m+3.
又∵x m>3的解集为x>-1,∴2m+3=-1,解得m=-2.
3.[2020·潍坊]若定义一种新运算:a b=例如:3 1=3-1=2;5 4=5+4-6=3.
则函数y=(x+2) (x-1)的图象
大致是 ( )
图Z4-1
A
[解析]根据a b=可分两种情况:当x≤4时,
(x+2) (x-1)=(x+2)-(x-1)=x+2-x+1=3,即:y=3;
当x>4时,(x+2) (x-1)=(x+2)+(x-1)-6=x+2+x-1-6=2x-5,
即:y=2x-5,A选项符合题意,故选A.
4.四则运算符号有+,-,×,÷,现引入两个新运算符号∨,∧,合称“六则运算”.a∨b的运算结果是a和b中较大的数,a∧b的运算结果是a和b中较小的数.下列等式不一定成立的是 ( )
A.(a∨b)+(a∧b)=a+b
B.(-a)∨(-b)=-(a∧b)
C.(a∨b)×c=(ac)∨(bc)
D.a-(b∨c)=(a-b)∧(a-c)
C
5.[2019·德州]已知:[x]表示不超过x的最大整数.例:[4.8]=4,
[-0.8]=-1.现定义:{x}=x-[x],例:{1.5}=1.5-[1.5]=0.5,则{3.9}+
{-1.8}-{1}= .
1.1
[解析]根据题意可得:{3.9}+{-1.8}-{1}=3.9-3-1.8+2-1+1=1.1,故答案为:1.1.
6.[2020·通辽]用※定义一种新运算:对于任意实数m和n,规定m※n=m2n-mn-3n,
如:1※2=12×2-1×2-3×2=-6.
(1)求(-2)※;
(2)若3※m≥-6,求m的取值范围,并在所给的数轴上表示出解集.
图Z4-2
解:(1)(-2)※=(-2)2×-(-2)×-3×=4+2-3=3.
(2)∵3※m=32m-3m-3m=3m,3※m≥-6,∴3m≥-6,得m≥-2.
在数轴上表示如下:
7.[2020·张家界]阅读下面材料:
对于实数a,b,我们定义符号min{a,b}的意义为:当a
根据上面的材料回答下列问题:
(1)min{-1,3}= ;
(2)当min时,求x的取值范围.
-1
(2)当min时,求x的取值范围.
(2)由题意得:≥,3(2x-3)≥2(x+2),6x-9≥2x+4,4x≥13,x≥,
∴x的取值范围为x≥.
求解新定义几何概念型问题的关键是弄清新概念的本质,将其与已学过的数学知识建立联系,并应用相关知识解决问题.
类型二
新定义几何概念型阅读题
1.如图Z4-3,若△ABC内一点P满足∠PAC
=∠PCB=∠PBA,则称点P为△ABC的
“布罗卡尔点”.三角形的布罗卡尔点
是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,“布罗卡尔点”的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,
∠ACB=120°,P为△ABC的“布罗卡尔点”,若PA=,则PB+PC=
.
图Z4-3
1+
[解析]如图,由“布罗卡尔点”的定义,设∠PAC=∠PCB=∠PBA=α,
又CA=CB,∠ACB=120°,
∴∠ABC=∠BAC=30°,∴∠CBP=∠PAB=30°-α=β,
∴△BCP∽△ABP,∴.
在△ABC中,作CD⊥AB于D,则BD=AB,
而cos∠ABC=,∴,∴,
∴PB=1,PC=,∴PB+PC=1+.
2.[2020·怀化]定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 .(填序号)
①平行四边形;②矩形;③菱形;④正方形.
(2)图形判定:如图Z4-4①,在四边形ABCD
中,AD∥BC,AC⊥BD,过点D作BD的垂线
交BC的延长线于点E,且∠DBC=45°,证明:四边形ABCD是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图②中,面积为24的垂等四边形ABCD内接于☉O中,
∠BCD=60°.求☉O的半径.
图Z4-4
(1)下面四边形是垂等四边形的是 .(填序号)
①平行四边形;②矩形;③菱形;④正方形.
④
[解析]①平行四边形的对角线互相平分但不垂直和相等,故不是垂等四边形;
②矩形对角线相等但不垂直,故不是垂等四边形;
③菱形的对角线互相垂直但不相等,故不是垂等四边形;
④正方形的对角线互相垂直且相等,故正方形是垂等四边形.
故选④.
(2)图形判定:如图Z4-4①,在四边形ABCD中,AD∥BC,AC⊥BD,过点D作BD的垂线交BC的延长线于点E,且∠DBC=45°,证明:四边形ABCD是垂等四边形.
图Z4-4
解:(2)证明:∵AC⊥BD,ED⊥BD,∴AC∥DE,
又∵AD∥BC,
∴四边形ADEC是平行四边形,∴AC=DE.
∵BD⊥DE,∠DBC=45°,
∴△BDE是等腰直角三角形,∴BD=DE,∴BD=AC,
又∵BD⊥AC,∴四边形ABCD是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图②中,面积为24的垂等四边形ABCD内接于☉O中,∠BCD=60°.求☉O的半径.
图Z4-4
(3)如图,过点O作OE⊥BD于点E,连接OD,
∵四边形ABCD是垂等四边形,
∴AC=BD,
又∵垂等四边形ABCD的面积是24,
∴AC·BD=24,解得AC=BD=4,
又∵∠BCD=60°,∴∠DOE=60°,
设半径为r,根据垂径定理可得:
在Rt△ODE中,OD=r,DE=2,
∴r==4,
∴☉O的半径为4.
3.[2021·枣庄]如图Z4-5①,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图②,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗 请说明理由.
(2)性质探究:如图①,垂美四边
形ABCD的对角线AC,BD交于
点O.猜想:AB2+CD2与AD2+BC2有什么关系 并证明你的猜想.
(3)解决问题:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE.已知AC=4,AB=5,求GE的长.
图Z4-5
(1)概念理解:如图②,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗 请说明理由.
图Z4-5
解:(1)四边形ABCD是垂美四边形.
理由:连接AC,BD,
∵AB=AD,∴点A在线段BD的垂直平分线上,
∵CB=CD,∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,
∴AC⊥BD,即四边形ABCD是垂美四边形.
(2)性质探究:如图①,垂美四边形ABCD的对角线AC,BD交于点O.猜想:AB2+CD2与AD2+BC2有什么关系 并证明你的猜想.
图Z4-5
(2)AD2+BC2=AB2+CD2.
证明:∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AD2+BC2=AB2+CD2.
(3)解决问题:如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,
连接CE,BG,GE.已知AC=4,AB=5,求GE的长.
图Z4-5
(3)如图,连接CG,BE.
∵四边形ACFG和四边形ABDE是正方形,
∴AG=AC,AE=AB,∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,
即∠GAB=∠CAE,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC.
设CE交AB于点M,
∵∠AEC+∠AME=90°,∠CMB=∠AME,
∴∠ABG+∠CMB=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,
∴BC=3,CG=4,BE=5,
∴GE2=CG2+BE2-CB2=73,
∵GE>0,∴GE=.
新方法型阅读题指材料中先给出一种新的解题方法,通过阅读体会新方法的实质,然后用新方法解决相关问题.
类型三
新方法型阅读题
1.[2020·常德]阅读理解:对于x3-(n2+1)x+n这类特殊的代数式可以按下面的方法分解因式:
x3-(n2+1)x+n=x3-n2x-x+n=x(x2-n2)-(x-n)=x(x-n)(x+n)-(x-n)=(x-n)
(x2+nx-1).
理解运用:如果x3-(n2+1)x+n=0,那么(x-n)(x2+nx-1)=0,即有x-n=0或x2+nx-1=0,因此,方程x-n=0和x2+nx-1=0的所有解就是方程
x3-(n2+1)x+n=0的解.
解决问题:方程x3-5x+2=0的解为 .
2或-1+或-1-
[解析]∵x3-5x+2=0,
∴x3-4x-x+2=0,∴x(x2-4)-(x-2)=0,
∴x(x+2)(x-2)-(x-2)=0,
则(x-2)[x(x+2)-1]=0,即(x-2)(x2+2x-1)=0,
∴x-2=0或x2+2x-1=0,解得x=2或x=-1±,故答案为2或-1+或-1-.
2.[2020·呼和浩特]“通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程x-=0,就可以利用该思维方式,设=y,将原方程转化为:y2-y=0这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.
已知实数x,y满足求x2+y2的值.
解:令xy=a,x+y=b,则原方程组可化为:
整理得:
②-①得:11a2=275,
解得:a2=25,代入②可得:b=4,
∴方程组的解为:或
x2+y2=(x+y)2-2xy=b2-2a,
当a=5时,x2+y2=6,
当a=-5时,x2+y2=26,
因此x2+y2的值为6或26.
3.[2021·遂宁]已知平面直角坐标系中,点P(x0,y0)和直线Ax+By+C=0(其中A,B不全为0),则点P到直线Ax+By+C=0的距离d可用公式d=来计算.
例如:求点P(1,2)到直线y=2x+1的距离,因为直线y=2x+1可化为2x-y+1=0,其中A=2,B=-1,C=1,所以点P(1,2)到直线y=2x+1的距离为:
d=.
根据以上材料,解答下列问题:
(1)求点M(0,3)到直线y=x+9的距离;
(2)在(1)的条件下,☉M的半径r=4,判断☉M与直线y=x+9的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.
解:(1)∵y=x+9可变形为x-y+9=0,
则其中A=,B=-1,C=9,
由公式得,点M(0,3)到直线y=x+9的距离d==3,
∴点M到直线y=x+9的距离为3.
(2)在(1)的条件下,☉M的半径r=4,判断☉M与直线y=x+9的位置关系,若相交,设其弦长为n,求n的值;若不相交,说明理由.
(2)如图,由(1)可知:圆心到直线的距离d=3,
∵圆的半径r=4,∴d
连接EM,过点M作MH⊥EF于H,则EF=2EH,
在Rt△EHM中,EM=4,MH=3,
根据勾股定理得,EH=,
∴弦长n=EF=2EH=2.
4.[2021·鄂州]数学课外活动小组的同学在学习了完全平方公式之后,针对两个正数之和与这两个正数之积的算术平方根的两倍之间的关系进行了探究,请阅读以下探究过程并解决问题.
猜想发现
由5+5=2=10;=2;0.4+0.4=2=0.8;
+5>2=2;0.2+3.2>2=1.6;>2.
猜想:如果a>0,b>0,那么存在a+b≥2(当且仅当a=b时等号成立).
猜想证明
∵()2≥0,∴①当且仅当=0,即a=b时,a-2+b
=0,∴a+b=2;
②当≠0,即a≠b时,a-2+b>0,∴a+b>2.
综合上述可得:若a>0,b>0,则a+b≥2成立(当且仅当a=b时等号成立).
猜想运用
对于函数y=x+(x>0),当x取何值时,函数y的值最小 最小值是多少
变式探究
对于函数y=+x(x>3),当x取何值时,函数y的值最小 最小值是多少
拓展应用
疫情期间,为了解决疑似人员的临时隔离问题,高速公路检测站入口处,检测人员利用检测站的一面墙(墙的长度不限),用63米长的钢丝网围成了9间相同的长方形隔离房,如图Z4-6.设每间隔离房的面积为S(米2).问:每间隔离房的长、宽各为多少时,可使每间隔离房的面积S最大 最大面积是多少
图Z4-6
猜想运用
对于函数y=x+(x>0),当x取何值时,函数y的值最小 最小值是多少
解:猜想运用
∵x>0,∴>0,∴y=x+≥2=2,
∴当x=时,ymin=2.此时x2=1,
∵x>0,
∴x=1,即x=1时,函数y的值最小,最小值为2.
变式探究
对于函数y=+x(x>3),当x取何值时,函数y的值最小 最小值是多
少
变式探究
∵x>3,∴x-3>0,>0,∴y=+x-3+3≥2+3=5,
∴当=x-3时,ymin=5,
此时(x-3)2=1,∴x1=4,x2=2(舍去),
即x=4时,函数y的值最小,最小值为5.
拓展应用
疫情期间,为了解决疑似人员的临时隔离问题,高速公路检测站入口处,检测人员利用检测站的一面墙(墙的长度不限),用63米长的钢丝网围成了9间相同的长方形隔离房,如图Z4-6.设每间隔离房的面积为S(米2).问:每间隔离房的长、宽各为多少时,可使每间隔离房的面积S最大 最大面积是多少
图Z4-6
拓展应用
设每间隔离房与墙平行的边为x米,与墙垂直的边为y米,依题意得:
9x+12y=63,即3x+4y=21.
∵3x>0,4y>0,∴3x+4y≥2,
即21≥2,整理得xy≤,即S≤,
∴当3x=4y时,Smax=,此时x=,y=,
即每间隔离房长为米,宽为米时,S的最大值为米2.
5.阅读下面材料:
某同学遇到这样一个问题:如图Z4-7①,△ABC中,AB=AC,点D在BC边上,过点B作BE⊥AD交AD延长线于点E,当BC=2AE时,图①中是否存在与AD相等的线段 若存在,请找出并说明理由;若不存在,说明理由.该同学通过探究发现,过点A作BC的垂线AF,垂足为F,能得到一对全等三角
形(如图②),从而将问题解决.
请回答:
图Z4-7
(1)该同学发现的与AD相等的线段是 .
(2)证明该同学所发现的结论.
参考该同学思考问题的方法,解决下面的问题:
(3)如图③,在△ABC中,AB=AC,∠BAC=90°,点D在BC上,点E是△ABC外一点,且AE=AD,∠DAE=45°,点F是BC中点,G在AB上,连接EF,DG,
∠EFC+∠AGD=90°,
求的值.
图Z4-7
BD
(2)证明该同学所发现的结论.
图Z4-7
解:(2)证明:∵△ABC是等腰三角形,
AF⊥BC,∴BC=2BF.
∵BC=2AE,∴BF=AE.
在Rt△ABF和Rt△BAE中,
∴Rt△ABF≌Rt△BAE(HL),
∴∠BAE=∠ABF,∴BD=AD.
参考该同学思考问题的方法,解决下面的问题:
(3)如图③,在△ABC中,AB=AC,∠BAC=90°,点D在BC上,点E是△ABC外一点,且AE=AD,∠DAE=45°,点F是BC中点,G在AB上,连接EF,DG,∠EFC+∠AGD=90°,求的值.
图Z4-7
(3)如图,连接AF,
∵AB=AC,∠BAC=90°,点F是BC中点,
∴AF⊥BC,∠BAF=∠BAC=45°,AF=BC,∴∠EFC+∠AFE=90°,
∵∠EFC+∠AGD=90°,∴∠AFE=∠AGD,
∵∠DAE=45°,∴∠BAF=∠DAE,
∴∠BAF+∠FAD=∠DAE+∠FAD,即∠GAD=∠FAE.
在△AGD和△AFE中,
∴△AGD≌△AFE,∴AG=AF.
∵AF=BC,∴AG=BC,∴.
1.[2021·襄阳]在△ABC中,∠ACB=90°,=m,D是边BC上一点,将△ABD沿AD折叠得到△AED,连接BE.
(1)特例发现 如图Z4-8①,当m=1,AE落在直线AC上时.
①求证:∠DAC=∠EBC;
②填空:的值为 ;
类型四
类比探究型阅读题
图Z4-8
(2)类比探究 如图②,当m≠1,AE与边BC相交时,在AD上取一点G,使∠ACG=∠BCE,CG交AE于点H,探究的值(用含m的式子表示),并写出探究过程;
(3)拓展运用 在(2)的条件下,当m=,
D是BC的中点时,若EB·EH=6,求CG的长.
图Z4-8
(1)特例发现 如图Z4-8①,当m=1,AE落在直线AC上时.
①求证:∠DAC=∠EBC;
图Z4-8
解:(1)①证明:方法一:当m=1,AE落在直线AC
上时,有AC=BC,而∠ACB=90°,于是
∠ABC=∠CAB=45°;
而由折叠知AB=AE,∠BAD=∠EAD=22.5°.
∵AB=AE,∠CAB=45°,
∴∠ABE=∠AEB==67.5°.
∴∠EBC=∠ABE-∠ABC=67.5°-45°=22.5°.∴∠DAC=∠EBC.
方法二:如图①,延长AD交BE于点F,则由折叠知AF⊥BE于点F,于是∠BFD=∠ACD=90°.
又∠BDF=∠ADC,
故∠DAC=∠EBC.
(1)特例发现 如图Z4-8①,当m=1,AE落在直线AC上时.
②填空:的值为 ;
图Z4-8
1
(2)类比探究 如图②,当m≠1,AE与边BC相交时,在AD上取一点G,使∠ACG=∠BCE,CG交AE于点H,探究的值(用含m的式子表示),并写出探究过程;
图Z4-8
(2)如图②,延长AD交BE于点F,由(1)①可知∠DAC=∠EBC.
又∵∠ACG=∠BCE,
∴△ACG∽△BCE.∴=m.
(3)拓展运用 在(2)的条件下,当m=,D是BC的中点时,若EB·EH=6,求CG的长.
图Z4-8
(3)如图②,由折叠知BF=EF,∠AFB=90°,
又∵D是BC的中点,∴DF∥CE.
∴∠BEC=∠BFA=90°,
∠GAH=∠CEH.
由(2)知△ACG∽△BCE,
从而∠AGC=∠BEC=90°,=m=.
∴,∴=tan∠GAC=.
设CG=x,则CE=x,AG=x,BE=2x,∴AG=CE.
又∵∠AHG=∠EHC,∴△AGH≌△ECH.
∴CH=GH,AH=EH,∴GH=x.
在Rt△AGH中,由勾股定理,得AH=x.
∵EB·EH=6,∴2x·x=6,∴x=±(负值舍去),∴CG=.
2.[2021·达州]某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
【观察与猜想】
(1)如图Z4-9①,在正方形ABCD中,
点E,F分别是AB,AD上的两点,连接
DE,CF,DE⊥CF,则的值为 ;
(2)如图②,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接
CE,BD,且CE⊥BD,则的值为 ;
图Z4-9
【类比探究】
(3)如图③,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE·AB=CF·AD;
图Z4-9
【拓展延伸】
(4)如图④,在Rt△ABD中,∠BAD=90°,AD=9,tan∠ADB=,将
△ABD沿BD翻折,点A落在点C处得△CBD,点E,F分别在边AB,AD上,连接DE,CF,DE⊥CF.
①求的值;
②连接BF,若AE=1,直接写出BF的长度.
图Z4-9
【观察与猜想】
(1)如图Z4-9①,在正方形ABCD
中,点E,F分别是AB,AD上的两点,
连接DE,CF,DE⊥CF,则的值为
;
图Z4-9
1
[解析]如图①,设DE与CF交于点G,
∵四边形ABCD是正方形,
∴∠A=∠FDC=90°,AD=CD,
∵DE⊥CF,∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,∴∠CFD=∠AED,
在△AED和△DFC中,
∴△AED≌△DFC(AAS),∴DE=CF,∴=1.
【观察与猜想】
(2)如图②,在矩形ABCD中,AD=7,CD=4,点E是AD上的一点,连接CE,BD,且CE⊥BD,则的值为 ;
图Z4-9
[解析]如图②,设DB与CE交于点G,
∵四边形ABCD是矩形,∴∠A=∠EDC=90°.
∵CE⊥BD,∴∠DGC=90°,
∴∠CDG+∠ECD=90°,∠ADB+∠CDG=90°,
∴∠ECD=∠ADB,
∵∠CDE=∠A,∴△DEC∽△ABD,∴.
【类比探究】
(3)如图③,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE·AB=CF·AD;
图Z4-9
(3)证明:如图③,过点C作CH⊥AF交AF的延长线于点H,
∵CG⊥EG,∴∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∵∠DFG=∠CFH,∴∠FCH=∠FDG,
∵∠ADE=∠FDG,∴∠FCH=∠ADE,
∵∠A=∠H,
∴△DEA∽△CFH,∴,∴,
∴DE·AB=CF·AD.
【拓展延伸】
(4)如图④,在Rt△ABD中,∠BAD=90°,AD=9,tan∠ADB=,将
△ABD沿BD翻折,点A落在点C处得△CBD,点E,F分别在边AB,AD上,连接DE,CF,DE⊥CF.
①求的值;
②连接BF,若AE=1,直接写出BF的长度.
图Z4-9
(4)①如图④,过点C作CG⊥AD于点G,连接AC交BD于点H,CG与DE相交于点O,则CH⊥BD.
∵CG⊥AD,CF⊥DE,
∴∠FCG+∠CFG=∠CFG+∠ADE=90°,
∴∠FCG=∠ADE,∠BAD=∠CGF=90°,
∴△DEA∽△CFG,∴.
在Rt△ABD中,tan∠ADB=,AD=9,∴AB=3,
在Rt△ADH中,tan∠ADH=,∴,
设AH=a,则DH=3a,
∵AH2+DH2=AD2,∴a2+(3a)2=92,
∴a=(负值已舍去),
∴AH=,DH=,
∴AC=2AH=.
∵S△ADC=AC·DH=AD·CG,
∴×9CG,
∴CG=,∴.
②BF=.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
