2022中考数学三轮冲刺专题突破05 几何模型及其应用 课件(124张)
文档属性
| 名称 | 2022中考数学三轮冲刺专题突破05 几何模型及其应用 课件(124张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-07 23:51:09 | ||
图片预览




文档简介
(共124张PPT)
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 05
几何模型及其应用
●方法点析
●题型精练
●题型分类
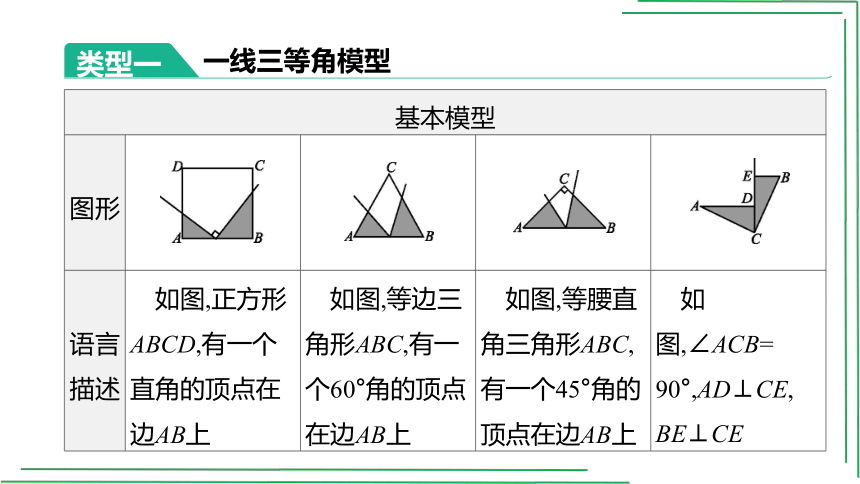
类型一
一线三等角模型
基本模型
图形
语言 描述 如图,正方形ABCD,有一个直角的顶点在边AB上 如图,等边三角形ABC,有一个60°角的顶点在边AB上 如图,等腰直角三角形ABC,有一个45°角的顶点在边AB上 如图,∠ACB=
90°,AD⊥CE,
BE⊥CE
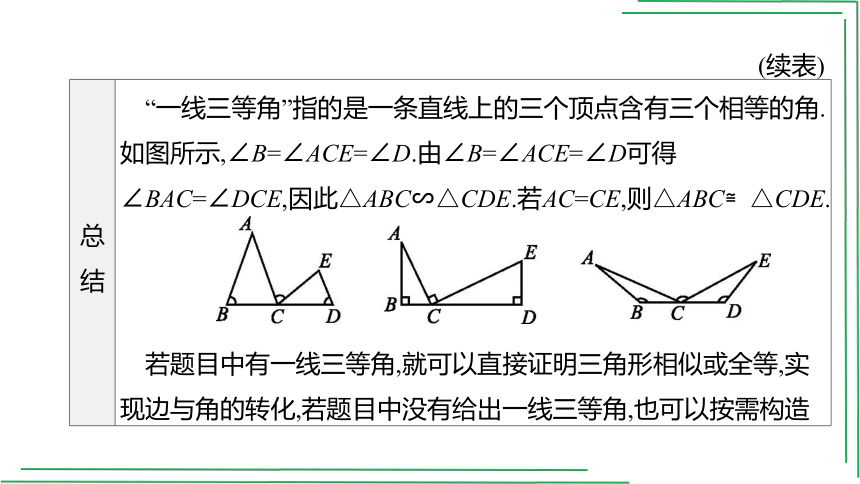
(续表)
总结 “一线三等角”指的是一条直线上的三个顶点含有三个相等的角.如图所示,∠B=∠ACE=∠D.由∠B=∠ACE=∠D可得∠BAC=∠DCE,因此△ABC∽△CDE.若AC=CE,则△ABC≌△CDE.
若题目中有一线三等角,就可以直接证明三角形相似或全等,实现边与角的转化,若题目中没有给出一线三等角,也可以按需构造
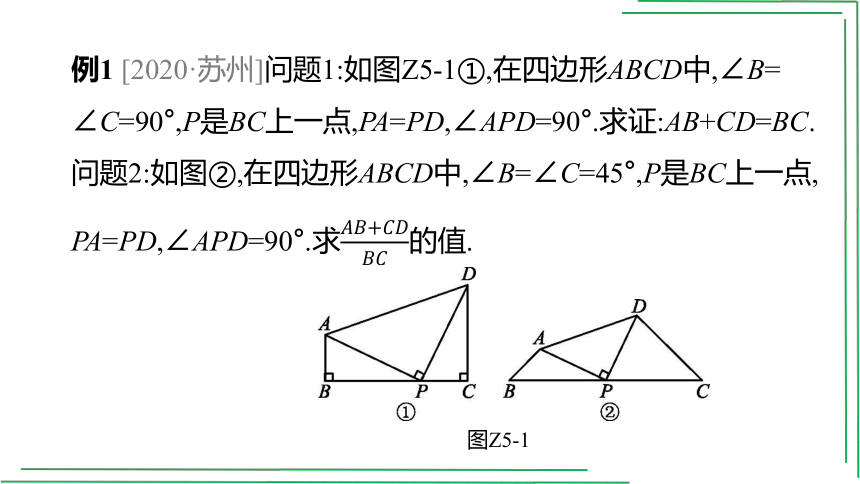
例1 [2020·苏州]问题1:如图Z5-1①,在四边形ABCD中,∠B=
∠C=90°,P是BC上一点,PA=PD,∠APD=90°.求证:AB+CD=BC.
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,
PA=PD,∠APD=90°.求的值.
图Z5-1
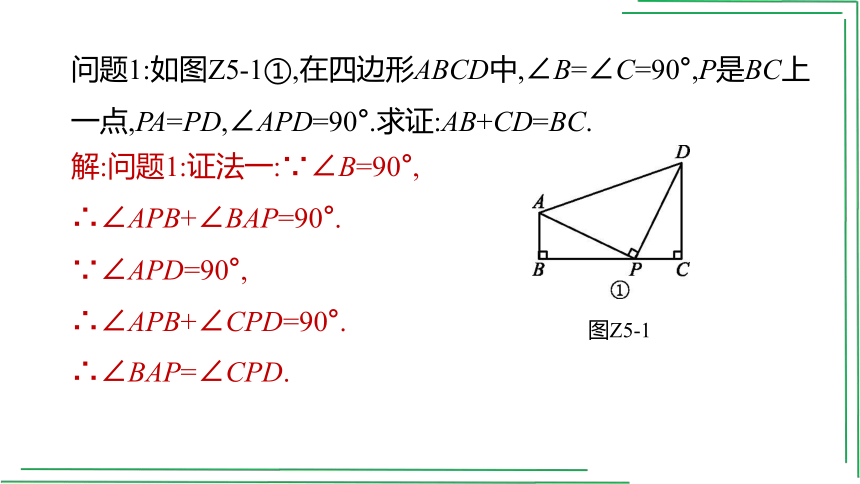
问题1:如图Z5-1①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,∠APD=90°.求证:AB+CD=BC.
图Z5-1
解:问题1:证法一:∵∠B=90°,
∴∠APB+∠BAP=90°.
∵∠APD=90°,
∴∠APB+∠CPD=90°.
∴∠BAP=∠CPD.
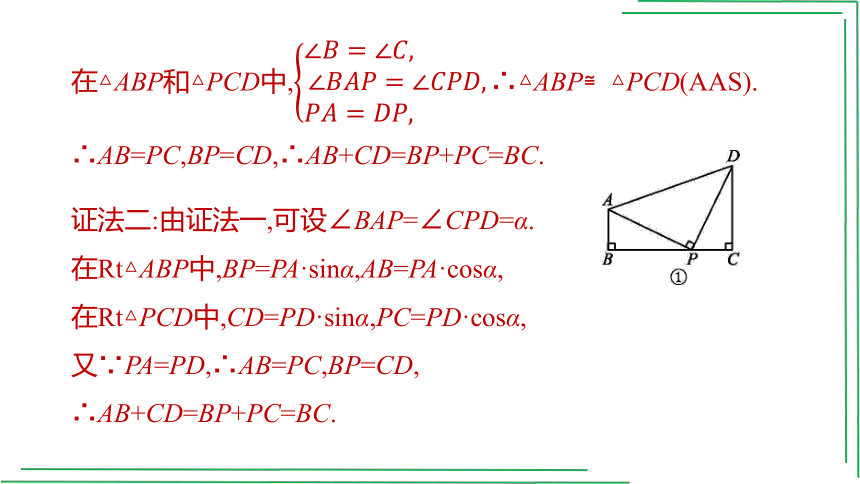
在△ABP和△PCD中,∴△ABP≌△PCD(AAS).
∴AB=PC,BP=CD,∴AB+CD=BP+PC=BC.
证法二:由证法一,可设∠BAP=∠CPD=α.
在Rt△ABP中,BP=PA·sinα,AB=PA·cosα,
在Rt△PCD中,CD=PD·sinα,PC=PD·cosα,
又∵PA=PD,∴AB=PC,BP=CD,
∴AB+CD=BP+PC=BC.
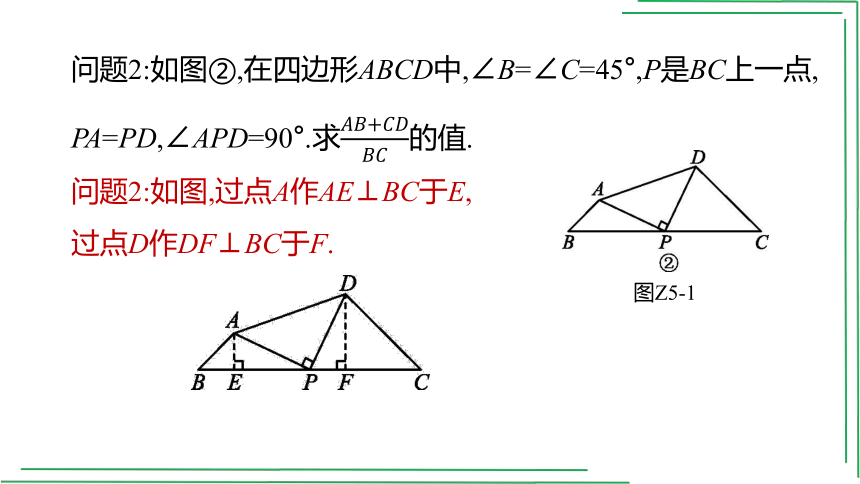
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,
PA=PD,∠APD=90°.求的值.
图Z5-1
问题2:如图,过点A作AE⊥BC于E,
过点D作DF⊥BC于F.
由问题1可知AE+DF=EF,
在Rt△ABE和Rt△DFC中,∠B=∠C=45°,
∴AE=BE,DF=CF,AB=AE,CD=DF.
∴BC=BE+EF+CF=2(AE+DF),AB+CD=(AE+DF).
∴.
|题型精练|
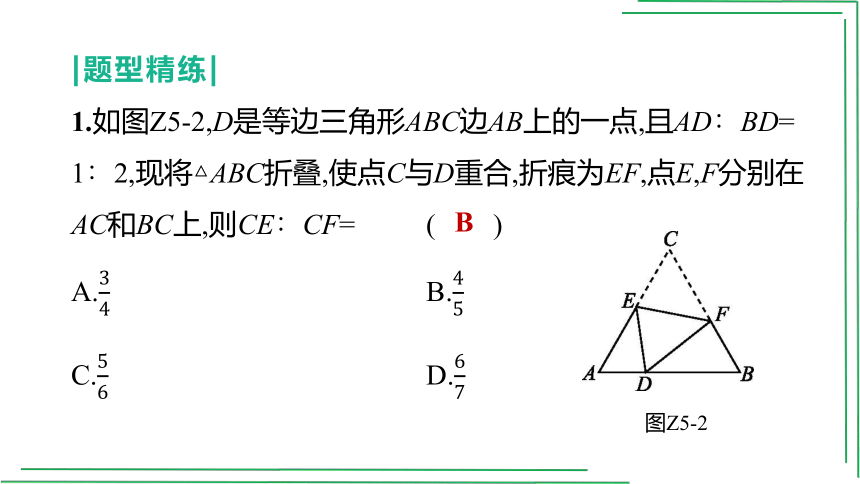
1.如图Z5-2,D是等边三角形ABC边AB上的一点,且AD∶BD=
1∶2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE∶CF= ( )
A. B.
C. D.
图Z5-2
B
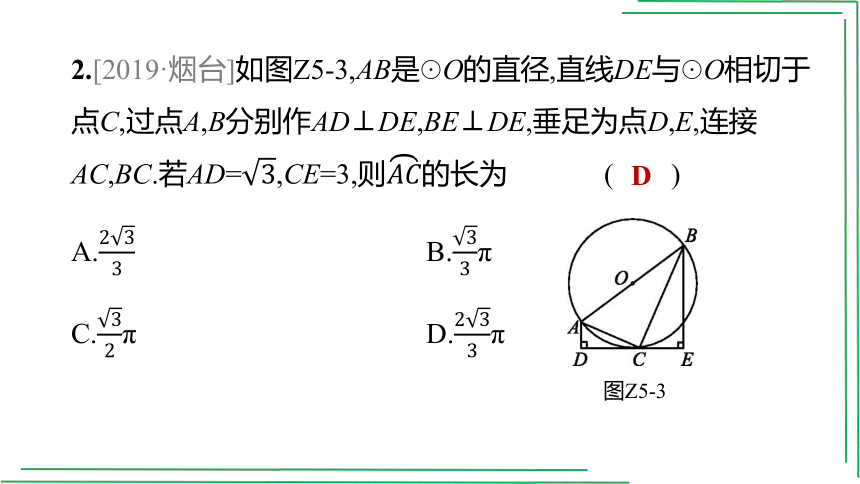
2.[2019·烟台]如图Z5-3,AB是☉O的直径,直线DE与☉O相切于点C,过点A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC.若AD=,CE=3,则的长为 ( )
A. B.π
C.π D.π
图Z5-3
D
[解析]连接OC,∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,∴∠DAC+∠ACD=90°,
∵AB是☉O的直径,∴∠ACB=90°,
∴∠BCE+∠ACD=90°,∴∠BCE=∠DAC.
在△ADC与△CEB中,
∵∠ADC=∠CEB=90°,∠BCE=∠DAC,
∴△ADC∽△CEB,
∴,在Rt△ACB中,tan∠BAC=,
∴∠BAC=60°,又∵OA=OC,∴△AOC是等边三角形,
∴∠ACO=∠AOC=60°,∵直线DE与☉O相切于点C,
∴OC⊥DE,∵AD⊥DE,∴AD∥OC,
∴∠DAC=∠ACO=60°,
∴AC=2AD=2,∴OA=AC=2,
∴的长为π.
3.一块直角三角板ABC按如图Z5-4放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为
.
图Z5-4
(-3-,3)
[解析]过B点作BE⊥x轴于点E,
由∠BEC=∠COA,∠EBC=90°-∠BCE=∠OCA可证△EBC∽△OCA,
∴,在Rt△ACO中,AC=,在Rt△ABC中,
∠CBA=30°,∴tan∠CBA=,
∴BC=,
∴,解得BE=3,EC=,
∴EO=EC+CO=+3,故答案为(-3-,3).
4.如图Z5-5,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③当△DCE为直角三角形时,BD的长为8或;④0的序号都填上)
图Z5-5
①②③④
[解析]∵AB=AC,∴∠B=∠C,又∵∠ADE=∠B,∴∠ADE=∠C,
∵∠DAE=∠CAD,∴△ADE∽△ACD.故①正确;
作AG⊥BC于G,∵AB=AC=10,∠ADE=∠B=α,cosα=,
∴cosB=,BC=2BG,
∴BC=2ABcosB=2×10×=16,
∵BD=6,∴DC=10,∴AB=DC,易知∠BAD=∠EDC,∠B=∠C,
∴△ABD≌△DCE(ASA).故②正确;
当∠AED=90°时,由①知△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,∴∠ADC=90°,
∴BD=ABcosB=8.
当∠CDE=90°时,易证△CDE∽△BAD,
∵∠CDE=90°,∴∠BAD=90°,
∵cosB=,AB=10,∴cosB=,∴BD=.故③正确;
易得△CDE∽△BAD,
∴,由②可知BC=16,
设BD=y,CE=x,∴,整理得:y2-16y+64=64-10x,
即(y-8)2=64-10x,∴05.如图Z5-6①,在矩形ABCD中,AB=10,点E为CD上一点,EF⊥BE交线段AD于点F,若EF=EB,AF=2.
(1)求AD的长;
(2)如图②,点G为线段DE上任意一点(不与点E重合),连接FG,GH
⊥FG交射线EB于点H,交EF于点O.
①求证:;
②连接AH,若GE=1,求S△ABH.
图Z5-6
(1)求AD的长;
图Z5-6
解:(1)∵四边形ABCD是矩形,
∴∠D=∠C=90°,
∵EF⊥BE,∴∠BEF=90°,
∴∠DEF+∠BEC=90°,
而在Rt△BEC中,∠BEC+∠EBC=90°,
∴∠DEF=∠EBC,
又∵EF=EB,∴△DEF≌△CBE,∴DF=CE,DE=BC,
设CE=x,则DF=x,∵AB=10,∴DE=10-x=BC,
又AF=2,AD=BC,∴AD=10-x,
∵AD=AF+FD,∴10-x=2+x,解得x=4,
∴AD=AF+FD=6.
(2)如图②,点G为线段DE上任意一点(不与点E重合),连接FG,GH⊥FG交射线EB于点H,交EF于点O.
①求证:;
②连接AH,若GE=1,求S△ABH.
图Z5-6
(2)①证明:连接FH,取FH中点记作点M,连接MG,ME,
∵FG⊥GH,∴∠FGH=90°,∴MG=FH=MF=MH,
∵∠HEF=90°,∴ME=FH=MF=MH,
∴MG=ME=MF=MH,
∴F,G,E,H在以M为圆心,MG为半径的圆上,
∴∠FHG=∠FEG,
∴tan∠FHG=tan∠FEG,∴,
由(1)知△DEF≌△CBE,∴DE=BC=AD,∴.
②连接AH,若GE=1,求S△ABH.
图Z5-6
②由(1)知DF=EC=4,故DE=6,
∵GE=1,∴DG=DE-GE=5,
由(2)①知∠FHG=∠FED,
∠FHG+∠GFH=90°,
∠FED+∠DFE=90°,∴∠GFH=∠DFE,
∴∠EFH=∠DFG,
∴tan∠EFH=tan∠DFG,∴,
∴EH>EF,∵EF=EB,即EH>EB,
∴H在点B的右侧,
如图,设EF=4x,则BE=4x,EH=5x,
∴BH=x,作EP⊥AB,HQ⊥AB,则HQ∥PE,
∴△PBE∽△QBH,∴=4,由(1)知AD=6,
∴QH=PE=AD=,∴S△ABH=·AB·QH=.
6.如图Z5-7,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=
∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,
且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线
上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=a时,P,Q两点间的距离(用
含a的代数式表示).
图Z5-7
(1)如图①,当点Q在线段AC上,且AP=AQ时,
求证:△BPE≌△CQE;
图Z5-7
证明:(1)∵E为BC的中点,∴BE=CE,
∵△ABC是等腰直角三角形,∴AB=AC,
∵AP=AQ,∴AB-AP=AC-AQ,即BP=CQ,
在△BPE和△CQE中,
∴△BPE≌△CQE.
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=a时,P,Q两点间的距离(用含a的代数式表示).
图Z5-7
(2)∵△ABC和△DEF是两个全等的
等腰直角三角形,
∴∠B=∠C=∠DEF=45°,
∵∠BEQ=∠EQC+∠C,
即∠BEP+∠DEF=∠EQC+∠C,
∴∠BEP+45°=∠EQC+45°,
∴∠BEP=∠EQC,∴△BPE∽△CEQ,∴,
∵BP=a,CQ=a,BE=CE,∴BE=CE=a,
∴BC=3a,∴AB=AC=BC·sin45°=3a,
∴AQ=CQ-AC=a,PA=AB-BP=2a,
连接PQ,
在Rt△APQ中,PQ=a.
类型二
手拉手模型
基本模型
图形
语言 描述 条件:CD∥AB,将△OCD旋转 条件:①~③中,△OAB,△OCD依次是等腰三角形、等腰直角三角形、等边三角形 条件:四边形OABC,四边形ODEF均为正方形
结论: △OCD∽△OAB 结论:①△OAC≌△OBD;②OP平分∠DPA 结论:△AOF≌△COD
总结 所谓手拉手模型,是指有公共顶点且顶角相等的两个等腰三角形、等腰直角三角形、等边三角形或正方形伴随旋转得出全等(相似).处于各种位置的旋转模型,因为顶点相连的四条边,形象地可以看作两双手,所以通常称为手拉手模型
(续表)
例2 如图Z5-8①,在△ABC中,∠BAC=90°,AB=AC,AO⊥BC于点O,F是线段AO上的点(不与A,O重合),∠EAF=90°,AE=AF,连接FE,FC,
BE,BF.
(1)求证:BE=BF;
(2)如图②,若将△AEF绕点A旋转,使边AF
在∠BAC的内部,延长CF交AB于点G,交BE于点K.
①求证:△AGC∽△KGB;
②当△BEF为等腰直角三角形时,请你直接写出AB∶BF的值.
图Z5-8
(1)求证:BE=BF;
图Z5-8
【分层分析】
(1)先证明△EAB≌△FAB,即可得到BE=BF;
解:(1)证明:∵AB=AC,AO⊥BC,
∴∠OAC=∠OAB=45°,
∴∠EAB=∠EAF-∠BAF=45°,∴∠EAB=∠BAF,
∵AE=AF,AB=AB,∴△EAB≌△FAB(SAS),∴BE=BF.
(2)如图②,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.
①求证:△AGC∽△KGB;
图Z5-8
【分层分析】
(2)①先证明△EAB≌△FAC,由全等三角形的性质可得:∠EBA=∠FCA,
进而可证明△AGC∽△KGB;
(2)①证明:∵∠BAC=90°,∠EAF=90°,
∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC,
∵AE=AF,AB=AC,
∴△AEB≌△AFC(SAS),∴∠EBA=∠FCA,
又∵∠KGB=∠AGC,∴△AGC∽△KGB.
②当△BEF为等腰直角三角形时,请你直接写出AB∶BF的值.
图Z5-8
【分层分析】
(2) ②由△AGC∽△KGB得∠GKB=∠GAC=90°,所以∠EBF<90°,由此可分两种情况讨论求值即可.
②AB∶BF=∶2或AB∶BF=∶2
|题型精练|
1.在锐角三角形ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图Z5-9①,当点C1在线段CA的
延长线上时,∠CC1A1= ;
(2)如图②,连接AA1,CC1.若△A1BA的
面积为4,则△CBC1的面积为 .
图Z5-9
90°
[解析](1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.
(2)由旋转的性质可知,BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
即∠ABA1=∠CBC1,∴△ABA1∽△CBC1.
∴=()2=()2=,
∵=4,∴.
2.如图Z5-10①,在Rt△ABC中,∠B=90°,cosC=,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为θ.当0°≤θ<360°时,的大小有无变化 请仅就图②的情况给出证明.
图Z5-10
解:当0°≤θ<360°时,的大小没有变化.证明如下:
∵cosC=,∴.
∵∠ECD=∠ACB,∴∠ECA=∠DCB.
又∵D,E分别是边BC,AC的中点,
∴,
∴△ECA∽△DCB,∴.
3.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE.
(1)如图Z5-11①,连接BG,DE.求证:BG=DE.
(2)如图②,如果正方形ABCD的边长为,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG∥BD,BG=BD.
①求∠BDE的度数;
②请写出正方形CEFG的边长.
图Z5-11
(1)如图Z5-11①,连接BG,DE.求证:BG=DE.
图Z5-11
解:(1)证明:∵四边形ABCD和
四边形CEFG都为正方形,
∴BC=DC,CG=CE,
∠BCD=∠GCE=90°.
∴∠BCD+∠DCG=∠GCE+∠DCG,
∴∠BCG=∠DCE.
∴△BCG≌△DCE(SAS).∴BG=DE.
(2)如图②,如果正方形ABCD的边长为,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG∥BD,BG=BD.
①求∠BDE的度数;
②请写出正方形CEFG的边长.
图Z5-11
(2)①连接BE.
由(1)可知:BG=DE.
∵CG∥BD,
∴∠DCG=∠BDC=45°,
∴∠BCG=∠BCD+∠GCD=90°+45°=135°.
∵∠GCE=90°,
∴∠BCE=360°-∠BCG-∠GCE=360°-135°-90°=135°,
∴∠BCG=∠BCE.
又∵BC=BC,CG=CE,∴△BCG≌△BCE(SAS),
∴BG=BE.
∵BG=DE,∴BD=BE=DE,
∴△BDE为等边三角形.∴∠BDE=60°.
②请写出正方形CEFG的边长.
图Z5-11
②延长EC交BD于点H,
在△DCE和△BCE中,
DE=BE,DC=BC,CE=CE,
∴△DCE≌△BCE(SSS),
∴∠BEC=∠DEC,
∴EH⊥BD,BH=BD.
∵BC=CD=,在Rt△BCD中,由勾股定理得
BD==2.∴BH=1,∴CH=1.
在Rt△BHE中,由勾股定理,得EH=,
∴CE=-1.∴正方形CEFG的边长为-1.
4.[2020·潍坊]如图Z5-12①,在△ABC中,∠A=90°,AB=AC=+1,点D,E分别在边AB,AC上,且AD=AE=1,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),如图②,连接CE,BD,CD.
(1)当0°<α<180°时,求证:CE=BD;
(2)如图③,当α=90°时,延长CE交
BD于点F,求证:CF垂直平分BD;
(3)在旋转过程中,求△BCD的面积
的最大值,并写出此时旋转角α的度数.
图Z5-12
(1)当0°<α<180°时,求证:CE=BD;
图Z5-12
解:(1)证明:根据题意知
AB=AC,AD=AE,∠CAB=∠EAD=90°,
∵∠CAE+∠BAE=∠BAD+∠BAE=90°,
∴∠CAE=∠BAD,
在△ACE和△ABD中,
∴△ACE≌△ABD(SAS),∴CE=BD.
(2)如图③,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;
图Z5-12
(2)证明:根据题意知AB=AC,AD=AE,
∠CAB=∠EAD=90°,
在△ACE和△ABD中,
∴△ACE≌△ABD(SAS),∴∠ACE=∠ABD,
∵∠ACE+∠AEC=90°,且∠AEC=∠FEB,
∴∠ABD+∠FEB=90°,∴∠EFB=90°,∴CF⊥BD.
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,
∴BC=AB=+2,CD=AC+AD=+2,
∴BC=CD,
∵CF⊥BD,∴CF垂直平分BD.
(3)在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.
(3)△BCD中,边BC的长是定值,则BC边上
的高取最大值时△BCD的面积取最大值,
如图,延长DA交BC于G,则DA⊥BC时,
△BCD的面积取得最大值,
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,DG⊥BC于G,
∴AG=BC=,∠GAB=45°,
∴DG=AG+AD=+1=,∠DAB=180°-45°=135°,
∴△BCD的面积的最大值为:BC·DG=×(+2)×,旋转角α=135°.
类型三
对角互补模型
基本模型
类型 全等型-90° 全等型-120° 全等型-任意角α
图形
语言 描述 条件:如图,①∠AOB= ∠DCE=90°, ②OC平分∠AOB 条件:如图,①∠AOB= 2∠DCE=120°, ②OC平分∠AOB 条件:如图,①∠AOB=
2α,∠DCE=180°-2α,
②CD=CE
(续表)
基本模型
类型 全等型-90° 全等型-120° 全等型-任意角α
图形
语言 描述 结论:①CD=CE; ②OD+OE=OC; ③S四边形ODCE=S△OCD+ S△OCE=OC2 结论:①CD=CE; ②OD+OE=OC; ③S四边形ODCE=S△OCD+ S△OCE=OC2 结论:①OC平分∠AOB;
②OD+OE=2OC·cosα;
③S四边形ODCE=S△OCD+
S△OCE=OC2·sinα·cosα
例3 在△ABC中,∠ACB=90°,AC=BC,AB=2,现将一块三角板的直角顶点放在AB的中点D处,两直角边分别与直线AC,直线BC相交于点E,F,我们把DE⊥AC时的位置定为起始位置(如图Z5-13①),将三角板绕点D顺时针方向旋转一个角度α(0°<α<90°).
(1)如图Z5-13②,在旋转过程中,
当点E在线段AC上时,试判断
△DEF的形状,并说明理由.
(2)设直线ED交直线BC于点G,在旋转过程中,是否存在点G,使得△EFG为等腰三角形 若存在,求出CG的长;若不存在,请说明理由.
图Z5-13
(1)如图Z5-13②,在旋转过程中,当点E在线段AC上时,试判断△DEF的形状,并说明理由.
图Z5-13
【分层分析】
(1)△DEF中边DE和DF间的数量关系可以通过证明哪两个三角形全等得到;
解:(1)△DEF是等腰直角三角形.
理由如下:如图①,连接CD,
∵AC=BC,∠ACB=90°,D为AB的中点,
∴CD平分∠ACB,CD⊥AB.
∴∠ACD=∠DCB=∠B=45°,∴CD=DB=1.
∵∠EDC+∠CDF=∠CDF+∠FDB=90°,
∴∠EDC=∠FDB.
在△DCE和△DBF中,
∴△DCE≌△DBF(ASA),∴DE=DF.
又∵∠EDF=90°,∴△DEF是等腰直角三角形.
(2)设直线ED交直线BC于点G,在旋转过程中,是否存在点G,使得△EFG为等腰三角形 若存在,求出CG的长;若不存在,请说明理由.
图Z5-13
【分层分析】
(2)分三种情况考虑:点G在线段CB的延长线上;G与B重合;
G在线段BC上.
(2)存在.如图②,当点G在线段CB的延长线上时,
∵∠FGE<45°,∠FEG=45°,∠EFG>90°,
∴△EFG不可能是等腰三角形;
如图③,当G与B重合时,E与A重合,F与C重合,
此时FE=FG,∴△EFG为等腰三角形,CG=;
如图④,当G在线段BC上时,连接CD.
∵∠EGF>45°,∠EFG>45°,∠FEG=45°,∴只能EF=EG,
∵EC⊥FG,∴FC=CG.∵∠EDF=90°,∴∠FDG=90°,
∴DC=FG=CG,∴CG=1.综上,CG的值为或1.
|题型精练|
1.[2021·合肥包河区一模]如图Z5-14,点P为∠MON的平分线上一点,∠APB的两边分别与射线OM,ON交于A,B两点,∠APB绕点P旋转时始终满足OA·OB=OP2,若∠MON=54°,则∠APB的度数为 ( )
A.153° B.144°
C.163° D.162°
图Z5-14
A
[解析] ∵OP平分∠MON,
∴∠AOP=∠BOP=27°,
∵OA·OB=OP2,即,
∴△AOP∽△POB,∴∠OAP=∠OPB,
∵∠AOP+∠OAP+∠APO=180°,∴∠OAP+∠APO=153°,
∴∠OPB+∠APO=153°,即∠APB=153°.
2.如图Z5-15,四边形ABCD中,∠BAC=∠BDC=90°,AB=AC,
AC,BD交于点E,BD=4,CD=,则AD的长为 ( )
A.2 B.3 C.4 D.3
图Z5-15
B
[解析]如图,过点A作AF⊥AD交BD于点F,则∠BAF=∠CAD,
又∠BAC=∠BDC=90°,∠AEB=∠DEC,
∴∠ABF=∠ACD,
∵AB=AC,∴△ABF≌△ACD(ASA),
∴AF=AD,BF=CD,∴DF=BD-BF=3.
∵△ADF为等腰直角三角形,∴AD==3.
3.如图Z5-16,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,过点E作EF⊥BE,垂足为E,直线EF交线段DC于点F,则
= .
图Z5-16
[解析]方法一:如图,过点E作EM⊥BC于点M,EN⊥DC于点N,
∴∠CME=∠FNE=90°,
∵∠MCN=90°,∴四边形MENC是矩形,
∴∠MEN=90°,∴∠NEF+∠MEF=90°,
又∵EF⊥BE,∴∠BEF=90°,即∠MEB+∠MEF=90°,
∴∠NEF=∠MEB,∴△NEF∽△MEB,∴,
∵∠ABC=∠EMC=90°,∠ECM=∠ACB,
∴△ECM∽△ACB,∴.
方法二:如图,连接BF,取BF的中点O,连接OE,OC.
∵四边形ABCD是矩形,EF⊥BE,
∴∠BEF=∠BCF=90°,AB=CD=3,BC=AD=5.
∵O为BF中点,∴OE=OB=OF=OC,
∴B,C,F,E四点共圆,∴∠EBF=∠ECF,
∴tan∠EBF=tan∠ACD,∴.
4.如图Z5-17,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,则BC+CD= .
图Z5-17
4
[解析]如图,延长CB到E,使BE=DC,连接AE,AC.
∵∠BAD=90°,∠BCD=90°,
∴∠ABC+∠D=360°-90°-90°=180°.
∵∠ABC+∠ABE=180°,
∴∠ABE=∠D.
又∵BE=DC,AB=AD,∴△ABE≌△ADC,
∴AE=AC,∠EAB=∠DAC,
∴∠EAC=90°,∴S△AEC=AE2=EC2.
∵S△AEC=S四边形ABCD=12,∴EC2=12,∴EC=4,
∴BC+CD=BC+BE=EC=4.
5.已知△ABC是☉O的内接三角形,AB=AC,在∠BAC所对优弧BC上任取一点D,连接AD,BD,CD.
(1)如图Z5-18①,若∠BAC=120°,求证:BD+CD=AD;
(2)如图②,若∠BAC=α,那么
BD+CD与AD之间的数量关
系是什么
图Z5-18
(1)如图Z5-18①,若∠BAC=120°,求证:BD+CD=AD;
图Z5-18
解:(1)证明:如图,过点A作AE⊥BD于E,
AF⊥CD交DC的延长线于F,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∴∠ADB=∠ADC=30°,
∴AE=AF,
易得Rt△ADE≌Rt△ADF(HL),∴DE=DF,
易得Rt△ABE≌Rt△ACF(HL),∴BE=CF,
∴BD+CD=BE+DE+CD=2DE=AD.
(2)如图②,若∠BAC=α,那么BD+CD与AD之间的数量关系是什么
图Z5-18
(2)如图,作∠DAG=∠CAB交DB的延长线于点G,则△ABG≌△ACD,∴BG=CD,AG=AD.
过点A作AH⊥BD于H,则∠HAD=,DG=2DH,
∴BD+CD=DG=2DH=2AD·sin.
6.在等边三角形ABC中,点D是线段BC的中点,∠EDF=120°,射线DE与线段AB相交于点E,射线DF与线段AC(或AC的延长线)相交于点F.
(1)如图Z5-19①,若DF⊥AC,直接写出DE与AB的位置关系;
(2)如图②,将(1)中的∠EDF绕点D顺时
针旋转一定的角度,DF仍与线段AC相
交于点F,求证:DE=DF;
(3)在∠EDF绕点D顺时针旋转过程中,直接
用等式表示线段BE,CF,AB之间的数量关系;
(4)当∠EDF绕点D顺时针旋转到如图③的位置时,DF与线段AC的延长线相交于点F,作DN⊥AC于点N,若DN=FN,AB=10,直接写出BE+CF的值.
图Z5-19
(1)如图Z5-19①,若DF⊥AC,直接写出DE与AB的位置关系;
解:(1)DE⊥AB.
图Z5-19
(2)如图②,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F,求证:DE=DF;
图Z5-19
(2)证明:如图①,作DP⊥AB,DQ⊥AC,
垂足分别为P,Q,连接AD.
∵等边三角形ABC中,点D是
线段BC的中点,
∴AD平分∠BAC,∴DP=DQ.
∵∠AQD=∠APD=90°,∠BAC=60°,
∴∠PDQ=360°-60°-90°-90°=120°,
∴∠PDQ=∠EDF,∴∠EDP=∠FDQ.
在△EPD和△FQD中,
∴△EDP≌△FDQ,∴DE=DF.
(3)在∠EDF绕点D顺时针旋转过程中,直接用等式表示线段BE,CF,AB之间的数量关系;
图Z5-19
(3)分两种情况,
①当E,F分别在AB,AC边上时,
如图①,
∵△EDP≌△FDQ,∴EP=FQ,
∴BE+CF=BP+EP+CQ-QF=
BP+CQ=BD+CD=AB;
②当点F在AC延长线上时,如图②,作DM⊥AB于M,DN'⊥AC于N',易得△DME≌△DN'F,∴EM=N'F,
∴BE-CF=BM+ME-CF=CN'+N'F-CF=2N'C=CD=AB.
(4)当∠EDF绕点D顺时针旋转到如图③的位置时,DF与线段AC的延长线相交于点F,作DN⊥AC于点N,若DN=FN,AB=10,直接写出BE+CF的值.
图Z5-19
(4)BE+CF=5.
类型四
十字架模型
基本模型
图形
结论 △ABE≌ △BCF, AE=BF HF=GE △ABG≌ △DAF, FG=DF-BG 四边形MNOP是正方形(弦图) △CDE∽
△BCD,
例4 (1)如图Z5-20①,四边形ABCD为正方形,BF⊥AE,那么BF与AE相等吗 为什么
(2)如图②,在Rt△ABC中,BA=BC,∠ABC=90°,D为BC边的中点,BE⊥
AD于点E,交AC于F,求AF∶FC的值;
(3)如图③,Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=3,
BC=4,求CF.
图Z5-20
(1)如图Z5-20①,四边形ABCD为正方形,BF⊥AE,那么BF与AE相等吗 为什么
图Z5-20
【分层分析】
(1)先判断出AB=AD,再利用同角的余角相等,得∠ABF=∠DAE,进而可得△ABF≌△DAE,即可得出结论;
解:(1)BF=AE,理由:
∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠D=90°,
∴∠BAE+∠DAE=90°.
∵AE⊥BF,∴∠BAE+∠ABF=90°,∴∠ABF=∠DAE.
在△ABF和△DAE中,
∴△ABF≌△DAE,∴BF=AE.
(2)如图②,在Rt△ABC中,BA=BC,∠ABC=90°,D为BC边的中点,
BE⊥AD于点E,交AC于F,求AF∶FC的值;
图Z5-20
【分层分析】
(2)在十字架模型的启示下,构造出正方形ABCM,延长BF交CM于G;
(2)如图,过点A作AM∥BC,过点C作CM∥AB,两线相交于M,延长BF交CM于G,∴四边形ABCM是平行四边形.
∵∠ABC=90°,∴ ABCM是矩形.
∵AB=BC,∴矩形ABCM是正方形,∴AB=BC=CM.
同(1)的方法得,△ABD≌△BCG,∴CG=BD.
∵点D是BC中点,∴BD=BC=CM,
∴CG=CM=AB.
∵AB∥CM,∴△AFB∽△CFG,∴=2.
(3)如图③,Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=3,BC=4,求CF.
图Z5-20
【分层分析】
(3)先构造出矩形ABCN,再延长BF交CN于P.
(3)如图,在Rt△ABC中,AB=3,BC=4,
∴AC=5,
∵点D是BC中点,∴BD=BC=2,
过点A作AN∥BC,过点C作CN∥AB,
两线相交于N,延长BF交CN于P,
∴四边形ABCN是平行四边形,
∵∠ABC=90°,∴ ABCN是矩形,
同(1)的方法得,∠BAD=∠CBP,
∵∠ABD=∠BCP=90°,∴△ABD∽△BCP,∴,
∴,∴CP=,
同(2)的方法,△CFP∽△AFB,
∴,∴,
∴CF=.
|题型精练|
1.如图Z5-21,将边长为4的正方形纸片ABCD折叠,使得点A落在CD的中点E处,折痕为FG,点F在AD边上,则折痕FG的长为 ( )
A.5 B.2
C.2 D.2
图Z5-21
B
[解析]连接AE,根据正方形内十字架结构可得FG=AE,而AE==2,故选:B.
2.如图Z5-22,在矩形ABCD中,AB=-1,BC=2,过D点作DE⊥AC交BC于F点,则的值为 ( )
A. B.
C. D.
图Z5-22
D
[解析]由△CDF∽△BCA可得,即CF==3-,∴,故选:D.
3.如图Z5-23,在Rt△ACB中,AC=4,BC=3,点D为AC上一点,连接
BD,E为AB上一点,CE⊥BD,AD=CD时,则CE的长为 .
图Z5-23
[解析]见CE⊥BD联想十字架结构,补图成矩形ACBH,得△BCD∽△CAG,则,即,得AG=,CG=,由△AEG∽△BEC可得
,即,解得CE=.
4.将一张边长为4 cm的正方形纸片沿MN对折,使点D落在BC边上.
(1)若点D与点B重合,则折痕MN的长为 ;
(2)如图Z5-24,若点D落在BC的中点E处,
则折痕MN的长为 .
图Z5-24
4 cm
2cm
[解析](1)当点D与点B重合时,折痕MN与对角线AC重合,
∵AC==4,
∴折痕MN为4 cm.
(2)若点D落在BC的中点E处,MN=DE,
此时DE==2 cm.
5.如图Z5-25①,在矩形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,
∠1=∠2.
(1)①求证:EF∥AC;②若,求的值;
(2)联系拓展:如图②,在四边形EFGH中,∠EFG=90°,EF=EH=10,GF=GH=5,
EM⊥HN,点M,N分别在边FG,EF上,
求的值.
图Z5-25
(1)①求证:EF∥AC;②若,求的值;
图Z5-25
解:(1)①证明:∵四边形ABCD是矩形,
∴AD∥BF,
∵AE=CF,∴四边形ACFE是平行四边形,
∴EF∥AC.
②∵∠1=∠2,∠1+∠EBC=90°,∴∠2+∠EBC=90°,∴∠BHC=90°,
∵EF∥AC,∴∠F=∠2,∠BHC=∠BEF=∠ABC=90°,
∴△BEF∽△ABC,∴.
(2)联系拓展:如图②,在四边形EFGH中,∠EFG=90°,EF=EH=10,
GF=GH=5,EM⊥HN,点M,N分别在边FG,EF上,求的值.
图Z5-25
(2)如图,作矩形PEFQ,连接EG,
∴∠P=∠Q=90°,PE=QF,
△EHG≌△EFG(SSS),
∴∠EHG=90°,∴∠EHP+∠GHQ=90°,
∵∠PEH+∠EHP=90°,∴∠PEH=∠QHG,
∴△EPH∽△HQG,∴,
∵EF=EH=10,GF=GH=5,∴=2,
设QG=x,则PH=2x,QH=10-2x,PE=20-4x,
∴20-4x=5+x,∴x=3,
∴PE=8,∴.
6.如图Z5-26①,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF,交点为G.若正方形的边长为4.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到
△BPF(如图②),延长FP交BA
的延长线于点Q,求AQ的长;
(3)将△ABE绕点A按逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图③),若AM和BF相交于点N,求四边形MNGH的面积.
图Z5-26
(1)求证:AE⊥BF;
图Z5-26
解:(1)证明:∵E,F分别是正方形ABCD
边BC,CD的中点,∴CF=BE.
在△ABE和△BCF中,
∴△ABE≌△BCF(SAS),∴∠BAE=∠CBF.
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,∴∠BGE=90°,∴AE⊥BF.
(2)将△BCF沿BF对折,得到△BPF(如图②),延长FP交BA的延长线于点Q,求AQ的长;
图Z5-26
(2)根据题意得,FP=FC,∠PFB=∠BFC,
∠FPB=90°,
∵CD∥AB,∴∠CFB=∠ABF,
∴∠ABF=∠PFB,∴QF=QB.
∵PF=FC=2,PB=BC=4.
在Rt△BPQ中,设QB=x,∴x2=(x-2)2+42,∴x=5,∴AQ=BQ-AB=5-4=1.
(3)将△ABE绕点A按逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图③),若AM和BF相交于点N,求四边形MNGH的面积.
图Z5-26
(3)∵正方形边长为4,∠BAE=∠EAM,AE⊥BF,
∴AN=AB=4.
∵∠AHM=90°,∴GN∥HM,∴△AGN∽△AHM,
∴=()2,∴=()2,∴S△AGN=,
∴S四边形GHMN=S△AHM-S△AGN=4-.
类型五
角含半角模型
基本模型
图形
语言 描述 条件:如图, ①AB=AD; ②∠B+∠D=180°;③2∠EAF=∠BAD. 结论:EF=BE+DF 条件:等腰直角三角形ABC中,AB=AC, ∠DAE=45°. 结论:BD2+CE2=DE2 条件:正方形ABCD中,
∠EAF=45°,BG=DF,G,B,C在同一条直线上.
结论:①△GAE≌△FAE;
②EF=BE+DF;③△EFC的周长=2AB;④A点到EF的距离=AB
(续表)
总结 解决角含半角模型问题常用旋转方法,涉及的知识点主要是全等
|题型精练|
例5 如图Z5-27,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为 ( )
A.2 B.3 C. D.
图Z5-27
A
[解析]如图,由基本模型可得EF=GF,
在Rt△BCE中,
由勾股定理得BE==3,
在Rt△AEF中,设AF=x,
则DF=6-x,EF=FG=3+(6-x)=9-x,
所以(9-x)2=9+x2,解得x=4,即DF=2,
所以CF==2,故选A.
【方法点析】利用旋转是解决角含半角模型的基本方法,借用勾股定理,利用方程思想是求相应线段的关键.
|题型精练|
1.如图Z5-28,在正方形ABCD中,E,F分别是边BC,CD上的点,
∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为 ( )
A.2 B.3 C.4 D.5
图Z5-28
A
[解析]如图,将△DAF绕点A顺时针旋转90°得到△BAG,易证G,B,C三点共线,由△FAE≌△GAE得EF=EG,△ECF的周长=EF+CF+CE=BE+BG+CF+CE=2BC=4,故正方形的边长为2.
2.如图Z5-29,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是 ( )
A.1 B.1.5 C.2 D.2.5
图Z5-29
C
[解析]∵△ABG沿AG对折至△AFG,
∴∠AFG=90°,AB=AF,GB=GF=3.
连接AE.∵四边形ABCD是正方形,∴AB=AD=AF.
又AE=AE,∴Rt△AFE≌Rt△ADE(HL).∴DE=EF.
设DE=x,则EF=DE=x,GE=x+3,CE=6-x.
在Rt△CGE中,由勾股定理得CG2+CE2=GE2,
∴32+(6-x)2=(x+3)2,解得x=2.故选C.
3.如图Z5-30,等腰三角形ABC中,∠BAC=120°,AB=AC,点M,N在边BC上,M在N的左侧,且∠MAN=60°,若BM=2,NC=3,则MN的长为 .
图Z5-30
[解析]如图,把△ABM绕点A逆时针旋转120°得△ACP,连接PN,
过点P作PD⊥BC,垂足为点D,则△ABM≌△ACP,PC=BM=2,MN=PN(易证),∠NCP=60°,所以CD=PC=1,PD=,因为DN=CN-CD=2,所以MN=PN=.
4.已知正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM=DN时,如图Z5-31①,则线段BM,DN和MN之间的数量关系是 .
(2)当∠MAN绕点A旋转到BM≠DN时,如图②,线段BM,DN和MN之间有怎样的数量关系 写出猜想,并加以证明.
(3)当∠MAN绕点A旋转到如图③的位置
时,线段BM,DN和MN之间又有怎样的数
量关系 请直接写出你的猜想.
图Z5-31
(1)当∠MAN绕点A旋转到BM=DN时,如图Z5-31①,则线段BM,DN和MN之间的数量关系是 .
图Z5-31
BM+DN=MN
[解析]如图①,连接AC,交MN于点G.
∵四边形ABCD为正方形,∴BC=CD,且CA平分∠BCD,
又∵BM=DN,∴CM=CN,
∴AC⊥MN,且MG=GN,
∴∠MAG=∠NAG.
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,∴∠BAM=∠GAN=∠GAM,
∴△ABM≌△AGM(AAS),
∴BM=MG,同理可得GN=DN,
∴BM+DN=MG+GN=MN.
故答案为:BM+DN=MN.
(2)当∠MAN绕点A旋转到BM≠DN时,如图②,线段BM,DN和MN之间有怎样的数量关系 写出猜想,并加以证明.
图Z5-31
(2)猜想:BM+DN=MN,证明如下:
如图②,在MB的延长线上截取
BE=DN,连接AE.
在△ABE和△ADN中,
∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
∵∠BAD=90°,∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠EAB+∠BAM=45°,∴∠EAM=∠NAM.
在△AEM和△ANM中,
∴△AEM≌△ANM(SAS),∴ME=MN.
又ME=BE+BM=BM+DN,
∴BM+DN=MN.
(3)当∠MAN绕点A旋转到如图③的位置时,线段BM,DN和MN之间又有怎样的数量关系 请直接写出你的猜想.
图Z5-31
(3)DN-BM=MN.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 05
几何模型及其应用
●方法点析
●题型精练
●题型分类
类型一
一线三等角模型
基本模型
图形
语言 描述 如图,正方形ABCD,有一个直角的顶点在边AB上 如图,等边三角形ABC,有一个60°角的顶点在边AB上 如图,等腰直角三角形ABC,有一个45°角的顶点在边AB上 如图,∠ACB=
90°,AD⊥CE,
BE⊥CE
(续表)
总结 “一线三等角”指的是一条直线上的三个顶点含有三个相等的角.如图所示,∠B=∠ACE=∠D.由∠B=∠ACE=∠D可得∠BAC=∠DCE,因此△ABC∽△CDE.若AC=CE,则△ABC≌△CDE.
若题目中有一线三等角,就可以直接证明三角形相似或全等,实现边与角的转化,若题目中没有给出一线三等角,也可以按需构造
例1 [2020·苏州]问题1:如图Z5-1①,在四边形ABCD中,∠B=
∠C=90°,P是BC上一点,PA=PD,∠APD=90°.求证:AB+CD=BC.
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,
PA=PD,∠APD=90°.求的值.
图Z5-1
问题1:如图Z5-1①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,∠APD=90°.求证:AB+CD=BC.
图Z5-1
解:问题1:证法一:∵∠B=90°,
∴∠APB+∠BAP=90°.
∵∠APD=90°,
∴∠APB+∠CPD=90°.
∴∠BAP=∠CPD.
在△ABP和△PCD中,∴△ABP≌△PCD(AAS).
∴AB=PC,BP=CD,∴AB+CD=BP+PC=BC.
证法二:由证法一,可设∠BAP=∠CPD=α.
在Rt△ABP中,BP=PA·sinα,AB=PA·cosα,
在Rt△PCD中,CD=PD·sinα,PC=PD·cosα,
又∵PA=PD,∴AB=PC,BP=CD,
∴AB+CD=BP+PC=BC.
问题2:如图②,在四边形ABCD中,∠B=∠C=45°,P是BC上一点,
PA=PD,∠APD=90°.求的值.
图Z5-1
问题2:如图,过点A作AE⊥BC于E,
过点D作DF⊥BC于F.
由问题1可知AE+DF=EF,
在Rt△ABE和Rt△DFC中,∠B=∠C=45°,
∴AE=BE,DF=CF,AB=AE,CD=DF.
∴BC=BE+EF+CF=2(AE+DF),AB+CD=(AE+DF).
∴.
|题型精练|
1.如图Z5-2,D是等边三角形ABC边AB上的一点,且AD∶BD=
1∶2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE∶CF= ( )
A. B.
C. D.
图Z5-2
B
2.[2019·烟台]如图Z5-3,AB是☉O的直径,直线DE与☉O相切于点C,过点A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC.若AD=,CE=3,则的长为 ( )
A. B.π
C.π D.π
图Z5-3
D
[解析]连接OC,∵AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,∴∠DAC+∠ACD=90°,
∵AB是☉O的直径,∴∠ACB=90°,
∴∠BCE+∠ACD=90°,∴∠BCE=∠DAC.
在△ADC与△CEB中,
∵∠ADC=∠CEB=90°,∠BCE=∠DAC,
∴△ADC∽△CEB,
∴,在Rt△ACB中,tan∠BAC=,
∴∠BAC=60°,又∵OA=OC,∴△AOC是等边三角形,
∴∠ACO=∠AOC=60°,∵直线DE与☉O相切于点C,
∴OC⊥DE,∵AD⊥DE,∴AD∥OC,
∴∠DAC=∠ACO=60°,
∴AC=2AD=2,∴OA=AC=2,
∴的长为π.
3.一块直角三角板ABC按如图Z5-4放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为
.
图Z5-4
(-3-,3)
[解析]过B点作BE⊥x轴于点E,
由∠BEC=∠COA,∠EBC=90°-∠BCE=∠OCA可证△EBC∽△OCA,
∴,在Rt△ACO中,AC=,在Rt△ABC中,
∠CBA=30°,∴tan∠CBA=,
∴BC=,
∴,解得BE=3,EC=,
∴EO=EC+CO=+3,故答案为(-3-,3).
4.如图Z5-5,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③当△DCE为直角三角形时,BD的长为8或;④0
图Z5-5
①②③④
[解析]∵AB=AC,∴∠B=∠C,又∵∠ADE=∠B,∴∠ADE=∠C,
∵∠DAE=∠CAD,∴△ADE∽△ACD.故①正确;
作AG⊥BC于G,∵AB=AC=10,∠ADE=∠B=α,cosα=,
∴cosB=,BC=2BG,
∴BC=2ABcosB=2×10×=16,
∵BD=6,∴DC=10,∴AB=DC,易知∠BAD=∠EDC,∠B=∠C,
∴△ABD≌△DCE(ASA).故②正确;
当∠AED=90°时,由①知△ADE∽△ACD,
∴∠ADC=∠AED,
∵∠AED=90°,∴∠ADC=90°,
∴BD=ABcosB=8.
当∠CDE=90°时,易证△CDE∽△BAD,
∵∠CDE=90°,∴∠BAD=90°,
∵cosB=,AB=10,∴cosB=,∴BD=.故③正确;
易得△CDE∽△BAD,
∴,由②可知BC=16,
设BD=y,CE=x,∴,整理得:y2-16y+64=64-10x,
即(y-8)2=64-10x,∴0
(1)求AD的长;
(2)如图②,点G为线段DE上任意一点(不与点E重合),连接FG,GH
⊥FG交射线EB于点H,交EF于点O.
①求证:;
②连接AH,若GE=1,求S△ABH.
图Z5-6
(1)求AD的长;
图Z5-6
解:(1)∵四边形ABCD是矩形,
∴∠D=∠C=90°,
∵EF⊥BE,∴∠BEF=90°,
∴∠DEF+∠BEC=90°,
而在Rt△BEC中,∠BEC+∠EBC=90°,
∴∠DEF=∠EBC,
又∵EF=EB,∴△DEF≌△CBE,∴DF=CE,DE=BC,
设CE=x,则DF=x,∵AB=10,∴DE=10-x=BC,
又AF=2,AD=BC,∴AD=10-x,
∵AD=AF+FD,∴10-x=2+x,解得x=4,
∴AD=AF+FD=6.
(2)如图②,点G为线段DE上任意一点(不与点E重合),连接FG,GH⊥FG交射线EB于点H,交EF于点O.
①求证:;
②连接AH,若GE=1,求S△ABH.
图Z5-6
(2)①证明:连接FH,取FH中点记作点M,连接MG,ME,
∵FG⊥GH,∴∠FGH=90°,∴MG=FH=MF=MH,
∵∠HEF=90°,∴ME=FH=MF=MH,
∴MG=ME=MF=MH,
∴F,G,E,H在以M为圆心,MG为半径的圆上,
∴∠FHG=∠FEG,
∴tan∠FHG=tan∠FEG,∴,
由(1)知△DEF≌△CBE,∴DE=BC=AD,∴.
②连接AH,若GE=1,求S△ABH.
图Z5-6
②由(1)知DF=EC=4,故DE=6,
∵GE=1,∴DG=DE-GE=5,
由(2)①知∠FHG=∠FED,
∠FHG+∠GFH=90°,
∠FED+∠DFE=90°,∴∠GFH=∠DFE,
∴∠EFH=∠DFG,
∴tan∠EFH=tan∠DFG,∴,
∴EH>EF,∵EF=EB,即EH>EB,
∴H在点B的右侧,
如图,设EF=4x,则BE=4x,EH=5x,
∴BH=x,作EP⊥AB,HQ⊥AB,则HQ∥PE,
∴△PBE∽△QBH,∴=4,由(1)知AD=6,
∴QH=PE=AD=,∴S△ABH=·AB·QH=.
6.如图Z5-7,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=
∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,
且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线
上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=a时,P,Q两点间的距离(用
含a的代数式表示).
图Z5-7
(1)如图①,当点Q在线段AC上,且AP=AQ时,
求证:△BPE≌△CQE;
图Z5-7
证明:(1)∵E为BC的中点,∴BE=CE,
∵△ABC是等腰直角三角形,∴AB=AC,
∵AP=AQ,∴AB-AP=AC-AQ,即BP=CQ,
在△BPE和△CQE中,
∴△BPE≌△CQE.
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=a,CQ=a时,P,Q两点间的距离(用含a的代数式表示).
图Z5-7
(2)∵△ABC和△DEF是两个全等的
等腰直角三角形,
∴∠B=∠C=∠DEF=45°,
∵∠BEQ=∠EQC+∠C,
即∠BEP+∠DEF=∠EQC+∠C,
∴∠BEP+45°=∠EQC+45°,
∴∠BEP=∠EQC,∴△BPE∽△CEQ,∴,
∵BP=a,CQ=a,BE=CE,∴BE=CE=a,
∴BC=3a,∴AB=AC=BC·sin45°=3a,
∴AQ=CQ-AC=a,PA=AB-BP=2a,
连接PQ,
在Rt△APQ中,PQ=a.
类型二
手拉手模型
基本模型
图形
语言 描述 条件:CD∥AB,将△OCD旋转 条件:①~③中,△OAB,△OCD依次是等腰三角形、等腰直角三角形、等边三角形 条件:四边形OABC,四边形ODEF均为正方形
结论: △OCD∽△OAB 结论:①△OAC≌△OBD;②OP平分∠DPA 结论:△AOF≌△COD
总结 所谓手拉手模型,是指有公共顶点且顶角相等的两个等腰三角形、等腰直角三角形、等边三角形或正方形伴随旋转得出全等(相似).处于各种位置的旋转模型,因为顶点相连的四条边,形象地可以看作两双手,所以通常称为手拉手模型
(续表)
例2 如图Z5-8①,在△ABC中,∠BAC=90°,AB=AC,AO⊥BC于点O,F是线段AO上的点(不与A,O重合),∠EAF=90°,AE=AF,连接FE,FC,
BE,BF.
(1)求证:BE=BF;
(2)如图②,若将△AEF绕点A旋转,使边AF
在∠BAC的内部,延长CF交AB于点G,交BE于点K.
①求证:△AGC∽△KGB;
②当△BEF为等腰直角三角形时,请你直接写出AB∶BF的值.
图Z5-8
(1)求证:BE=BF;
图Z5-8
【分层分析】
(1)先证明△EAB≌△FAB,即可得到BE=BF;
解:(1)证明:∵AB=AC,AO⊥BC,
∴∠OAC=∠OAB=45°,
∴∠EAB=∠EAF-∠BAF=45°,∴∠EAB=∠BAF,
∵AE=AF,AB=AB,∴△EAB≌△FAB(SAS),∴BE=BF.
(2)如图②,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.
①求证:△AGC∽△KGB;
图Z5-8
【分层分析】
(2)①先证明△EAB≌△FAC,由全等三角形的性质可得:∠EBA=∠FCA,
进而可证明△AGC∽△KGB;
(2)①证明:∵∠BAC=90°,∠EAF=90°,
∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC,
∵AE=AF,AB=AC,
∴△AEB≌△AFC(SAS),∴∠EBA=∠FCA,
又∵∠KGB=∠AGC,∴△AGC∽△KGB.
②当△BEF为等腰直角三角形时,请你直接写出AB∶BF的值.
图Z5-8
【分层分析】
(2) ②由△AGC∽△KGB得∠GKB=∠GAC=90°,所以∠EBF<90°,由此可分两种情况讨论求值即可.
②AB∶BF=∶2或AB∶BF=∶2
|题型精练|
1.在锐角三角形ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图Z5-9①,当点C1在线段CA的
延长线上时,∠CC1A1= ;
(2)如图②,连接AA1,CC1.若△A1BA的
面积为4,则△CBC1的面积为 .
图Z5-9
90°
[解析](1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,
∴∠CC1B=∠C1CB=45°,
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.
(2)由旋转的性质可知,BA=BA1,BC=BC1,∠ABC=∠A1BC1,
∴,∠ABC+∠ABC1=∠A1BC1+∠ABC1,
即∠ABA1=∠CBC1,∴△ABA1∽△CBC1.
∴=()2=()2=,
∵=4,∴.
2.如图Z5-10①,在Rt△ABC中,∠B=90°,cosC=,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为θ.当0°≤θ<360°时,的大小有无变化 请仅就图②的情况给出证明.
图Z5-10
解:当0°≤θ<360°时,的大小没有变化.证明如下:
∵cosC=,∴.
∵∠ECD=∠ACB,∴∠ECA=∠DCB.
又∵D,E分别是边BC,AC的中点,
∴,
∴△ECA∽△DCB,∴.
3.已知四边形ABCD和四边形CEFG都是正方形,且AB>CE.
(1)如图Z5-11①,连接BG,DE.求证:BG=DE.
(2)如图②,如果正方形ABCD的边长为,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG∥BD,BG=BD.
①求∠BDE的度数;
②请写出正方形CEFG的边长.
图Z5-11
(1)如图Z5-11①,连接BG,DE.求证:BG=DE.
图Z5-11
解:(1)证明:∵四边形ABCD和
四边形CEFG都为正方形,
∴BC=DC,CG=CE,
∠BCD=∠GCE=90°.
∴∠BCD+∠DCG=∠GCE+∠DCG,
∴∠BCG=∠DCE.
∴△BCG≌△DCE(SAS).∴BG=DE.
(2)如图②,如果正方形ABCD的边长为,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG∥BD,BG=BD.
①求∠BDE的度数;
②请写出正方形CEFG的边长.
图Z5-11
(2)①连接BE.
由(1)可知:BG=DE.
∵CG∥BD,
∴∠DCG=∠BDC=45°,
∴∠BCG=∠BCD+∠GCD=90°+45°=135°.
∵∠GCE=90°,
∴∠BCE=360°-∠BCG-∠GCE=360°-135°-90°=135°,
∴∠BCG=∠BCE.
又∵BC=BC,CG=CE,∴△BCG≌△BCE(SAS),
∴BG=BE.
∵BG=DE,∴BD=BE=DE,
∴△BDE为等边三角形.∴∠BDE=60°.
②请写出正方形CEFG的边长.
图Z5-11
②延长EC交BD于点H,
在△DCE和△BCE中,
DE=BE,DC=BC,CE=CE,
∴△DCE≌△BCE(SSS),
∴∠BEC=∠DEC,
∴EH⊥BD,BH=BD.
∵BC=CD=,在Rt△BCD中,由勾股定理得
BD==2.∴BH=1,∴CH=1.
在Rt△BHE中,由勾股定理,得EH=,
∴CE=-1.∴正方形CEFG的边长为-1.
4.[2020·潍坊]如图Z5-12①,在△ABC中,∠A=90°,AB=AC=+1,点D,E分别在边AB,AC上,且AD=AE=1,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),如图②,连接CE,BD,CD.
(1)当0°<α<180°时,求证:CE=BD;
(2)如图③,当α=90°时,延长CE交
BD于点F,求证:CF垂直平分BD;
(3)在旋转过程中,求△BCD的面积
的最大值,并写出此时旋转角α的度数.
图Z5-12
(1)当0°<α<180°时,求证:CE=BD;
图Z5-12
解:(1)证明:根据题意知
AB=AC,AD=AE,∠CAB=∠EAD=90°,
∵∠CAE+∠BAE=∠BAD+∠BAE=90°,
∴∠CAE=∠BAD,
在△ACE和△ABD中,
∴△ACE≌△ABD(SAS),∴CE=BD.
(2)如图③,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;
图Z5-12
(2)证明:根据题意知AB=AC,AD=AE,
∠CAB=∠EAD=90°,
在△ACE和△ABD中,
∴△ACE≌△ABD(SAS),∴∠ACE=∠ABD,
∵∠ACE+∠AEC=90°,且∠AEC=∠FEB,
∴∠ABD+∠FEB=90°,∴∠EFB=90°,∴CF⊥BD.
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,
∴BC=AB=+2,CD=AC+AD=+2,
∴BC=CD,
∵CF⊥BD,∴CF垂直平分BD.
(3)在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.
(3)△BCD中,边BC的长是定值,则BC边上
的高取最大值时△BCD的面积取最大值,
如图,延长DA交BC于G,则DA⊥BC时,
△BCD的面积取得最大值,
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,DG⊥BC于G,
∴AG=BC=,∠GAB=45°,
∴DG=AG+AD=+1=,∠DAB=180°-45°=135°,
∴△BCD的面积的最大值为:BC·DG=×(+2)×,旋转角α=135°.
类型三
对角互补模型
基本模型
类型 全等型-90° 全等型-120° 全等型-任意角α
图形
语言 描述 条件:如图,①∠AOB= ∠DCE=90°, ②OC平分∠AOB 条件:如图,①∠AOB= 2∠DCE=120°, ②OC平分∠AOB 条件:如图,①∠AOB=
2α,∠DCE=180°-2α,
②CD=CE
(续表)
基本模型
类型 全等型-90° 全等型-120° 全等型-任意角α
图形
语言 描述 结论:①CD=CE; ②OD+OE=OC; ③S四边形ODCE=S△OCD+ S△OCE=OC2 结论:①CD=CE; ②OD+OE=OC; ③S四边形ODCE=S△OCD+ S△OCE=OC2 结论:①OC平分∠AOB;
②OD+OE=2OC·cosα;
③S四边形ODCE=S△OCD+
S△OCE=OC2·sinα·cosα
例3 在△ABC中,∠ACB=90°,AC=BC,AB=2,现将一块三角板的直角顶点放在AB的中点D处,两直角边分别与直线AC,直线BC相交于点E,F,我们把DE⊥AC时的位置定为起始位置(如图Z5-13①),将三角板绕点D顺时针方向旋转一个角度α(0°<α<90°).
(1)如图Z5-13②,在旋转过程中,
当点E在线段AC上时,试判断
△DEF的形状,并说明理由.
(2)设直线ED交直线BC于点G,在旋转过程中,是否存在点G,使得△EFG为等腰三角形 若存在,求出CG的长;若不存在,请说明理由.
图Z5-13
(1)如图Z5-13②,在旋转过程中,当点E在线段AC上时,试判断△DEF的形状,并说明理由.
图Z5-13
【分层分析】
(1)△DEF中边DE和DF间的数量关系可以通过证明哪两个三角形全等得到;
解:(1)△DEF是等腰直角三角形.
理由如下:如图①,连接CD,
∵AC=BC,∠ACB=90°,D为AB的中点,
∴CD平分∠ACB,CD⊥AB.
∴∠ACD=∠DCB=∠B=45°,∴CD=DB=1.
∵∠EDC+∠CDF=∠CDF+∠FDB=90°,
∴∠EDC=∠FDB.
在△DCE和△DBF中,
∴△DCE≌△DBF(ASA),∴DE=DF.
又∵∠EDF=90°,∴△DEF是等腰直角三角形.
(2)设直线ED交直线BC于点G,在旋转过程中,是否存在点G,使得△EFG为等腰三角形 若存在,求出CG的长;若不存在,请说明理由.
图Z5-13
【分层分析】
(2)分三种情况考虑:点G在线段CB的延长线上;G与B重合;
G在线段BC上.
(2)存在.如图②,当点G在线段CB的延长线上时,
∵∠FGE<45°,∠FEG=45°,∠EFG>90°,
∴△EFG不可能是等腰三角形;
如图③,当G与B重合时,E与A重合,F与C重合,
此时FE=FG,∴△EFG为等腰三角形,CG=;
如图④,当G在线段BC上时,连接CD.
∵∠EGF>45°,∠EFG>45°,∠FEG=45°,∴只能EF=EG,
∵EC⊥FG,∴FC=CG.∵∠EDF=90°,∴∠FDG=90°,
∴DC=FG=CG,∴CG=1.综上,CG的值为或1.
|题型精练|
1.[2021·合肥包河区一模]如图Z5-14,点P为∠MON的平分线上一点,∠APB的两边分别与射线OM,ON交于A,B两点,∠APB绕点P旋转时始终满足OA·OB=OP2,若∠MON=54°,则∠APB的度数为 ( )
A.153° B.144°
C.163° D.162°
图Z5-14
A
[解析] ∵OP平分∠MON,
∴∠AOP=∠BOP=27°,
∵OA·OB=OP2,即,
∴△AOP∽△POB,∴∠OAP=∠OPB,
∵∠AOP+∠OAP+∠APO=180°,∴∠OAP+∠APO=153°,
∴∠OPB+∠APO=153°,即∠APB=153°.
2.如图Z5-15,四边形ABCD中,∠BAC=∠BDC=90°,AB=AC,
AC,BD交于点E,BD=4,CD=,则AD的长为 ( )
A.2 B.3 C.4 D.3
图Z5-15
B
[解析]如图,过点A作AF⊥AD交BD于点F,则∠BAF=∠CAD,
又∠BAC=∠BDC=90°,∠AEB=∠DEC,
∴∠ABF=∠ACD,
∵AB=AC,∴△ABF≌△ACD(ASA),
∴AF=AD,BF=CD,∴DF=BD-BF=3.
∵△ADF为等腰直角三角形,∴AD==3.
3.如图Z5-16,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,连接BE,过点E作EF⊥BE,垂足为E,直线EF交线段DC于点F,则
= .
图Z5-16
[解析]方法一:如图,过点E作EM⊥BC于点M,EN⊥DC于点N,
∴∠CME=∠FNE=90°,
∵∠MCN=90°,∴四边形MENC是矩形,
∴∠MEN=90°,∴∠NEF+∠MEF=90°,
又∵EF⊥BE,∴∠BEF=90°,即∠MEB+∠MEF=90°,
∴∠NEF=∠MEB,∴△NEF∽△MEB,∴,
∵∠ABC=∠EMC=90°,∠ECM=∠ACB,
∴△ECM∽△ACB,∴.
方法二:如图,连接BF,取BF的中点O,连接OE,OC.
∵四边形ABCD是矩形,EF⊥BE,
∴∠BEF=∠BCF=90°,AB=CD=3,BC=AD=5.
∵O为BF中点,∴OE=OB=OF=OC,
∴B,C,F,E四点共圆,∴∠EBF=∠ECF,
∴tan∠EBF=tan∠ACD,∴.
4.如图Z5-17,在四边形ABCD中,∠A=∠C=90°,AB=AD,若这个四边形的面积为12,则BC+CD= .
图Z5-17
4
[解析]如图,延长CB到E,使BE=DC,连接AE,AC.
∵∠BAD=90°,∠BCD=90°,
∴∠ABC+∠D=360°-90°-90°=180°.
∵∠ABC+∠ABE=180°,
∴∠ABE=∠D.
又∵BE=DC,AB=AD,∴△ABE≌△ADC,
∴AE=AC,∠EAB=∠DAC,
∴∠EAC=90°,∴S△AEC=AE2=EC2.
∵S△AEC=S四边形ABCD=12,∴EC2=12,∴EC=4,
∴BC+CD=BC+BE=EC=4.
5.已知△ABC是☉O的内接三角形,AB=AC,在∠BAC所对优弧BC上任取一点D,连接AD,BD,CD.
(1)如图Z5-18①,若∠BAC=120°,求证:BD+CD=AD;
(2)如图②,若∠BAC=α,那么
BD+CD与AD之间的数量关
系是什么
图Z5-18
(1)如图Z5-18①,若∠BAC=120°,求证:BD+CD=AD;
图Z5-18
解:(1)证明:如图,过点A作AE⊥BD于E,
AF⊥CD交DC的延长线于F,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=30°,
∴∠ADB=∠ADC=30°,
∴AE=AF,
易得Rt△ADE≌Rt△ADF(HL),∴DE=DF,
易得Rt△ABE≌Rt△ACF(HL),∴BE=CF,
∴BD+CD=BE+DE+CD=2DE=AD.
(2)如图②,若∠BAC=α,那么BD+CD与AD之间的数量关系是什么
图Z5-18
(2)如图,作∠DAG=∠CAB交DB的延长线于点G,则△ABG≌△ACD,∴BG=CD,AG=AD.
过点A作AH⊥BD于H,则∠HAD=,DG=2DH,
∴BD+CD=DG=2DH=2AD·sin.
6.在等边三角形ABC中,点D是线段BC的中点,∠EDF=120°,射线DE与线段AB相交于点E,射线DF与线段AC(或AC的延长线)相交于点F.
(1)如图Z5-19①,若DF⊥AC,直接写出DE与AB的位置关系;
(2)如图②,将(1)中的∠EDF绕点D顺时
针旋转一定的角度,DF仍与线段AC相
交于点F,求证:DE=DF;
(3)在∠EDF绕点D顺时针旋转过程中,直接
用等式表示线段BE,CF,AB之间的数量关系;
(4)当∠EDF绕点D顺时针旋转到如图③的位置时,DF与线段AC的延长线相交于点F,作DN⊥AC于点N,若DN=FN,AB=10,直接写出BE+CF的值.
图Z5-19
(1)如图Z5-19①,若DF⊥AC,直接写出DE与AB的位置关系;
解:(1)DE⊥AB.
图Z5-19
(2)如图②,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F,求证:DE=DF;
图Z5-19
(2)证明:如图①,作DP⊥AB,DQ⊥AC,
垂足分别为P,Q,连接AD.
∵等边三角形ABC中,点D是
线段BC的中点,
∴AD平分∠BAC,∴DP=DQ.
∵∠AQD=∠APD=90°,∠BAC=60°,
∴∠PDQ=360°-60°-90°-90°=120°,
∴∠PDQ=∠EDF,∴∠EDP=∠FDQ.
在△EPD和△FQD中,
∴△EDP≌△FDQ,∴DE=DF.
(3)在∠EDF绕点D顺时针旋转过程中,直接用等式表示线段BE,CF,AB之间的数量关系;
图Z5-19
(3)分两种情况,
①当E,F分别在AB,AC边上时,
如图①,
∵△EDP≌△FDQ,∴EP=FQ,
∴BE+CF=BP+EP+CQ-QF=
BP+CQ=BD+CD=AB;
②当点F在AC延长线上时,如图②,作DM⊥AB于M,DN'⊥AC于N',易得△DME≌△DN'F,∴EM=N'F,
∴BE-CF=BM+ME-CF=CN'+N'F-CF=2N'C=CD=AB.
(4)当∠EDF绕点D顺时针旋转到如图③的位置时,DF与线段AC的延长线相交于点F,作DN⊥AC于点N,若DN=FN,AB=10,直接写出BE+CF的值.
图Z5-19
(4)BE+CF=5.
类型四
十字架模型
基本模型
图形
结论 △ABE≌ △BCF, AE=BF HF=GE △ABG≌ △DAF, FG=DF-BG 四边形MNOP是正方形(弦图) △CDE∽
△BCD,
例4 (1)如图Z5-20①,四边形ABCD为正方形,BF⊥AE,那么BF与AE相等吗 为什么
(2)如图②,在Rt△ABC中,BA=BC,∠ABC=90°,D为BC边的中点,BE⊥
AD于点E,交AC于F,求AF∶FC的值;
(3)如图③,Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=3,
BC=4,求CF.
图Z5-20
(1)如图Z5-20①,四边形ABCD为正方形,BF⊥AE,那么BF与AE相等吗 为什么
图Z5-20
【分层分析】
(1)先判断出AB=AD,再利用同角的余角相等,得∠ABF=∠DAE,进而可得△ABF≌△DAE,即可得出结论;
解:(1)BF=AE,理由:
∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠D=90°,
∴∠BAE+∠DAE=90°.
∵AE⊥BF,∴∠BAE+∠ABF=90°,∴∠ABF=∠DAE.
在△ABF和△DAE中,
∴△ABF≌△DAE,∴BF=AE.
(2)如图②,在Rt△ABC中,BA=BC,∠ABC=90°,D为BC边的中点,
BE⊥AD于点E,交AC于F,求AF∶FC的值;
图Z5-20
【分层分析】
(2)在十字架模型的启示下,构造出正方形ABCM,延长BF交CM于G;
(2)如图,过点A作AM∥BC,过点C作CM∥AB,两线相交于M,延长BF交CM于G,∴四边形ABCM是平行四边形.
∵∠ABC=90°,∴ ABCM是矩形.
∵AB=BC,∴矩形ABCM是正方形,∴AB=BC=CM.
同(1)的方法得,△ABD≌△BCG,∴CG=BD.
∵点D是BC中点,∴BD=BC=CM,
∴CG=CM=AB.
∵AB∥CM,∴△AFB∽△CFG,∴=2.
(3)如图③,Rt△ACB中,∠ABC=90°,D为BC边的中点,BE⊥AD于点E,交AC于F,若AB=3,BC=4,求CF.
图Z5-20
【分层分析】
(3)先构造出矩形ABCN,再延长BF交CN于P.
(3)如图,在Rt△ABC中,AB=3,BC=4,
∴AC=5,
∵点D是BC中点,∴BD=BC=2,
过点A作AN∥BC,过点C作CN∥AB,
两线相交于N,延长BF交CN于P,
∴四边形ABCN是平行四边形,
∵∠ABC=90°,∴ ABCN是矩形,
同(1)的方法得,∠BAD=∠CBP,
∵∠ABD=∠BCP=90°,∴△ABD∽△BCP,∴,
∴,∴CP=,
同(2)的方法,△CFP∽△AFB,
∴,∴,
∴CF=.
|题型精练|
1.如图Z5-21,将边长为4的正方形纸片ABCD折叠,使得点A落在CD的中点E处,折痕为FG,点F在AD边上,则折痕FG的长为 ( )
A.5 B.2
C.2 D.2
图Z5-21
B
[解析]连接AE,根据正方形内十字架结构可得FG=AE,而AE==2,故选:B.
2.如图Z5-22,在矩形ABCD中,AB=-1,BC=2,过D点作DE⊥AC交BC于F点,则的值为 ( )
A. B.
C. D.
图Z5-22
D
[解析]由△CDF∽△BCA可得,即CF==3-,∴,故选:D.
3.如图Z5-23,在Rt△ACB中,AC=4,BC=3,点D为AC上一点,连接
BD,E为AB上一点,CE⊥BD,AD=CD时,则CE的长为 .
图Z5-23
[解析]见CE⊥BD联想十字架结构,补图成矩形ACBH,得△BCD∽△CAG,则,即,得AG=,CG=,由△AEG∽△BEC可得
,即,解得CE=.
4.将一张边长为4 cm的正方形纸片沿MN对折,使点D落在BC边上.
(1)若点D与点B重合,则折痕MN的长为 ;
(2)如图Z5-24,若点D落在BC的中点E处,
则折痕MN的长为 .
图Z5-24
4 cm
2cm
[解析](1)当点D与点B重合时,折痕MN与对角线AC重合,
∵AC==4,
∴折痕MN为4 cm.
(2)若点D落在BC的中点E处,MN=DE,
此时DE==2 cm.
5.如图Z5-25①,在矩形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,
∠1=∠2.
(1)①求证:EF∥AC;②若,求的值;
(2)联系拓展:如图②,在四边形EFGH中,∠EFG=90°,EF=EH=10,GF=GH=5,
EM⊥HN,点M,N分别在边FG,EF上,
求的值.
图Z5-25
(1)①求证:EF∥AC;②若,求的值;
图Z5-25
解:(1)①证明:∵四边形ABCD是矩形,
∴AD∥BF,
∵AE=CF,∴四边形ACFE是平行四边形,
∴EF∥AC.
②∵∠1=∠2,∠1+∠EBC=90°,∴∠2+∠EBC=90°,∴∠BHC=90°,
∵EF∥AC,∴∠F=∠2,∠BHC=∠BEF=∠ABC=90°,
∴△BEF∽△ABC,∴.
(2)联系拓展:如图②,在四边形EFGH中,∠EFG=90°,EF=EH=10,
GF=GH=5,EM⊥HN,点M,N分别在边FG,EF上,求的值.
图Z5-25
(2)如图,作矩形PEFQ,连接EG,
∴∠P=∠Q=90°,PE=QF,
△EHG≌△EFG(SSS),
∴∠EHG=90°,∴∠EHP+∠GHQ=90°,
∵∠PEH+∠EHP=90°,∴∠PEH=∠QHG,
∴△EPH∽△HQG,∴,
∵EF=EH=10,GF=GH=5,∴=2,
设QG=x,则PH=2x,QH=10-2x,PE=20-4x,
∴20-4x=5+x,∴x=3,
∴PE=8,∴.
6.如图Z5-26①,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF,交点为G.若正方形的边长为4.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到
△BPF(如图②),延长FP交BA
的延长线于点Q,求AQ的长;
(3)将△ABE绕点A按逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图③),若AM和BF相交于点N,求四边形MNGH的面积.
图Z5-26
(1)求证:AE⊥BF;
图Z5-26
解:(1)证明:∵E,F分别是正方形ABCD
边BC,CD的中点,∴CF=BE.
在△ABE和△BCF中,
∴△ABE≌△BCF(SAS),∴∠BAE=∠CBF.
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,∴∠BGE=90°,∴AE⊥BF.
(2)将△BCF沿BF对折,得到△BPF(如图②),延长FP交BA的延长线于点Q,求AQ的长;
图Z5-26
(2)根据题意得,FP=FC,∠PFB=∠BFC,
∠FPB=90°,
∵CD∥AB,∴∠CFB=∠ABF,
∴∠ABF=∠PFB,∴QF=QB.
∵PF=FC=2,PB=BC=4.
在Rt△BPQ中,设QB=x,∴x2=(x-2)2+42,∴x=5,∴AQ=BQ-AB=5-4=1.
(3)将△ABE绕点A按逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图③),若AM和BF相交于点N,求四边形MNGH的面积.
图Z5-26
(3)∵正方形边长为4,∠BAE=∠EAM,AE⊥BF,
∴AN=AB=4.
∵∠AHM=90°,∴GN∥HM,∴△AGN∽△AHM,
∴=()2,∴=()2,∴S△AGN=,
∴S四边形GHMN=S△AHM-S△AGN=4-.
类型五
角含半角模型
基本模型
图形
语言 描述 条件:如图, ①AB=AD; ②∠B+∠D=180°;③2∠EAF=∠BAD. 结论:EF=BE+DF 条件:等腰直角三角形ABC中,AB=AC, ∠DAE=45°. 结论:BD2+CE2=DE2 条件:正方形ABCD中,
∠EAF=45°,BG=DF,G,B,C在同一条直线上.
结论:①△GAE≌△FAE;
②EF=BE+DF;③△EFC的周长=2AB;④A点到EF的距离=AB
(续表)
总结 解决角含半角模型问题常用旋转方法,涉及的知识点主要是全等
|题型精练|
例5 如图Z5-27,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3,且∠ECF=45°,则CF的长为 ( )
A.2 B.3 C. D.
图Z5-27
A
[解析]如图,由基本模型可得EF=GF,
在Rt△BCE中,
由勾股定理得BE==3,
在Rt△AEF中,设AF=x,
则DF=6-x,EF=FG=3+(6-x)=9-x,
所以(9-x)2=9+x2,解得x=4,即DF=2,
所以CF==2,故选A.
【方法点析】利用旋转是解决角含半角模型的基本方法,借用勾股定理,利用方程思想是求相应线段的关键.
|题型精练|
1.如图Z5-28,在正方形ABCD中,E,F分别是边BC,CD上的点,
∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为 ( )
A.2 B.3 C.4 D.5
图Z5-28
A
[解析]如图,将△DAF绕点A顺时针旋转90°得到△BAG,易证G,B,C三点共线,由△FAE≌△GAE得EF=EG,△ECF的周长=EF+CF+CE=BE+BG+CF+CE=2BC=4,故正方形的边长为2.
2.如图Z5-29,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是 ( )
A.1 B.1.5 C.2 D.2.5
图Z5-29
C
[解析]∵△ABG沿AG对折至△AFG,
∴∠AFG=90°,AB=AF,GB=GF=3.
连接AE.∵四边形ABCD是正方形,∴AB=AD=AF.
又AE=AE,∴Rt△AFE≌Rt△ADE(HL).∴DE=EF.
设DE=x,则EF=DE=x,GE=x+3,CE=6-x.
在Rt△CGE中,由勾股定理得CG2+CE2=GE2,
∴32+(6-x)2=(x+3)2,解得x=2.故选C.
3.如图Z5-30,等腰三角形ABC中,∠BAC=120°,AB=AC,点M,N在边BC上,M在N的左侧,且∠MAN=60°,若BM=2,NC=3,则MN的长为 .
图Z5-30
[解析]如图,把△ABM绕点A逆时针旋转120°得△ACP,连接PN,
过点P作PD⊥BC,垂足为点D,则△ABM≌△ACP,PC=BM=2,MN=PN(易证),∠NCP=60°,所以CD=PC=1,PD=,因为DN=CN-CD=2,所以MN=PN=.
4.已知正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM=DN时,如图Z5-31①,则线段BM,DN和MN之间的数量关系是 .
(2)当∠MAN绕点A旋转到BM≠DN时,如图②,线段BM,DN和MN之间有怎样的数量关系 写出猜想,并加以证明.
(3)当∠MAN绕点A旋转到如图③的位置
时,线段BM,DN和MN之间又有怎样的数
量关系 请直接写出你的猜想.
图Z5-31
(1)当∠MAN绕点A旋转到BM=DN时,如图Z5-31①,则线段BM,DN和MN之间的数量关系是 .
图Z5-31
BM+DN=MN
[解析]如图①,连接AC,交MN于点G.
∵四边形ABCD为正方形,∴BC=CD,且CA平分∠BCD,
又∵BM=DN,∴CM=CN,
∴AC⊥MN,且MG=GN,
∴∠MAG=∠NAG.
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,∴∠BAM=∠GAN=∠GAM,
∴△ABM≌△AGM(AAS),
∴BM=MG,同理可得GN=DN,
∴BM+DN=MG+GN=MN.
故答案为:BM+DN=MN.
(2)当∠MAN绕点A旋转到BM≠DN时,如图②,线段BM,DN和MN之间有怎样的数量关系 写出猜想,并加以证明.
图Z5-31
(2)猜想:BM+DN=MN,证明如下:
如图②,在MB的延长线上截取
BE=DN,连接AE.
在△ABE和△ADN中,
∴△ABE≌△ADN(SAS),∴AE=AN,∠EAB=∠NAD.
∵∠BAD=90°,∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠EAB+∠BAM=45°,∴∠EAM=∠NAM.
在△AEM和△ANM中,
∴△AEM≌△ANM(SAS),∴ME=MN.
又ME=BE+BM=BM+DN,
∴BM+DN=MN.
(3)当∠MAN绕点A旋转到如图③的位置时,线段BM,DN和MN之间又有怎样的数量关系 请直接写出你的猜想.
图Z5-31
(3)DN-BM=MN.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
