2022中考数学三轮冲刺专题突破06 几何综合型问题 课件(共108张PPT)
文档属性
| 名称 | 2022中考数学三轮冲刺专题突破06 几何综合型问题 课件(共108张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 08:43:20 | ||
图片预览





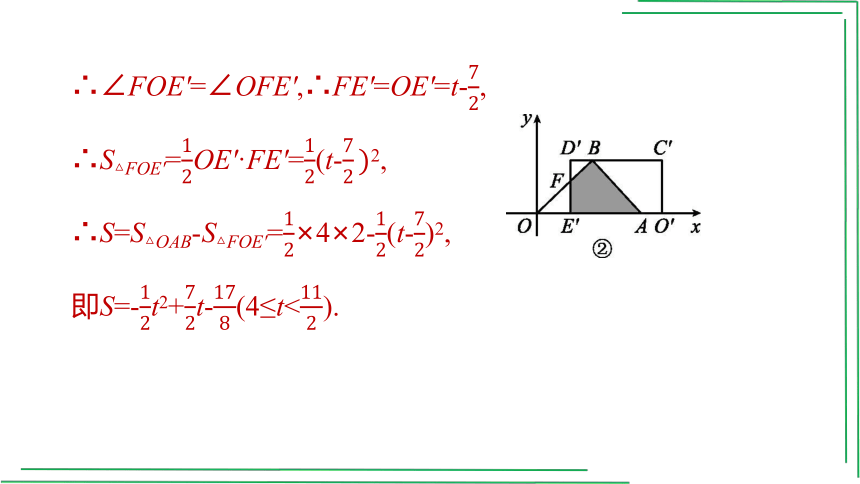


文档简介
(共108张PPT)
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 06
几何综合型问题
●方法点析
●题型精练
●题型分类
例1 [2021·天津24题节选]在平面直角坐标系中,O为原点,△OAB是等腰直角三角形,∠OBA=90°,BO=BA,顶点A(4,0),点B在第一象限,矩形OCDE的顶点
E(-,0),点C在y轴的正半轴上,点D在第二象限,射线DC经过点B.
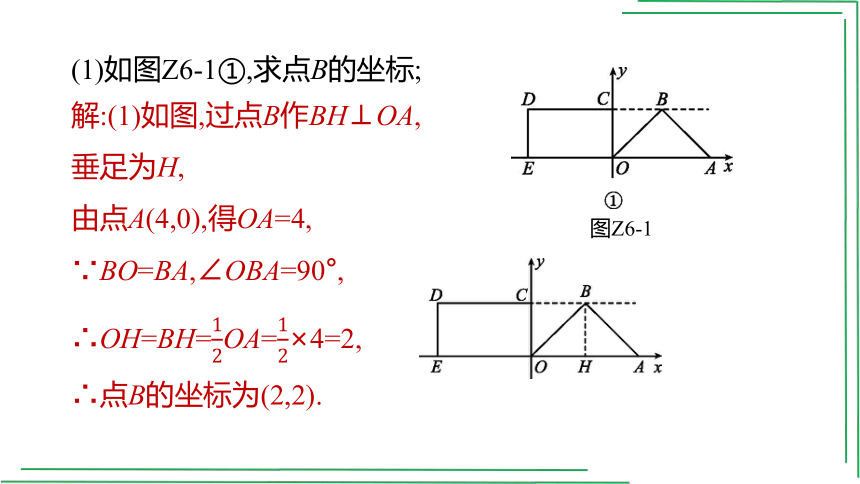
(1)如图Z6-1①,求点B的坐标;
(2)将矩形OCDE沿x轴向右平移,
得到矩形O'C'D'E',点O,C,D,E的
对应点分别为O',C',D',E'.设OO'=t,矩形O'C'D'E'与△OAB重叠部分的面积为S.如图②,当点E'在x轴正半轴上,且矩形O'C'D'E'与△OAB重叠部分为四边形时,
D'E'与OB相交于点F,试用含有t的式子表示S,并直接写出t的取值范围.
类型一
平移型问题
图Z6-1
(1)如图Z6-1①,求点B的坐标;
图Z6-1
解:(1)如图,过点B作BH⊥OA,垂足为H,
由点A(4,0),得OA=4,
∵BO=BA,∠OBA=90°,
∴OH=BH=OA=×4=2,
∴点B的坐标为(2,2).
(2)将矩形OCDE沿x轴向右平移,得到矩形O'C'D'E',点O,C,D,E的对应点分别为O',C',D',E'.设OO'=t,矩形O'C'D'E'与△OAB重叠部分的面积为S.如图②,当点E'在x轴正半轴上,且矩形O'C'D'E'与△OAB重叠部分为四边形时,
D'E'与OB相交于点F,试用含有t的式子
表示S,并直接写出t的取值范围.
图Z6-1
(2)由点E(-,0),得OE=,
由平移知,四边形O'C'D'E'是矩形,得∠O'E'D'=90°,O'E'=OE=,
∴OE'=OO'-O'E'=t-,∠FE'O=90°,
∵BO=BA,∠OBA=90°,
∴∠BOA=∠BAO=45°,
∴∠OFE'=90°-∠BOA=45°,
∴∠FOE'=∠OFE',∴FE'=OE'=t-,
∴S△FOE'=OE'·FE'=(t-2,
∴S=S△OAB-S△FOE'=×4×2-(t-)2,
即S=-t2+t-(4≤t<).
|题型精练|
问题情境:
小明将两个全等的Rt△ABC和Rt△DEF重叠在一起,其中∠ACB=∠DFE
=90°,∠ABC=∠DEF=30°,AC=1.固定△DEF不动,将△ABC沿直线ED向左平移,当点B与点D重合时停止移动.
猜想证明:
(1)如图Z6-2①,在平移过程中,当D为AB的
中点时,连接DC,CF,BF,请你猜想四边形
CDBF的形状,并证明你的结论.
图Z6-2
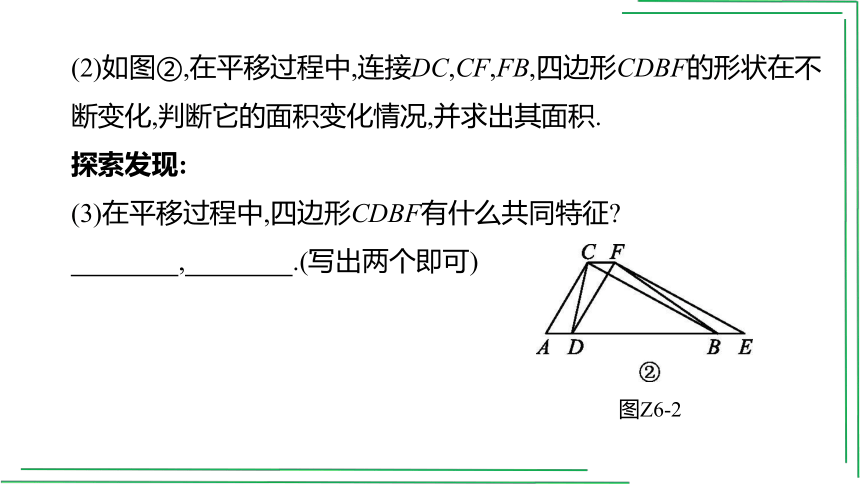
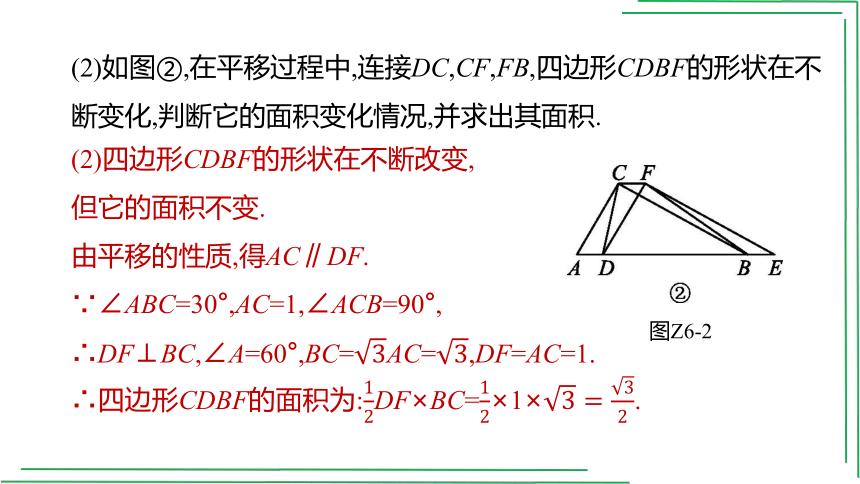
(2)如图②,在平移过程中,连接DC,CF,FB,四边形CDBF的形状在不断变化,判断它的面积变化情况,并求出其面积.
探索发现:
(3)在平移过程中,四边形CDBF有什么共同特征
, .(写出两个即可)
图Z6-2
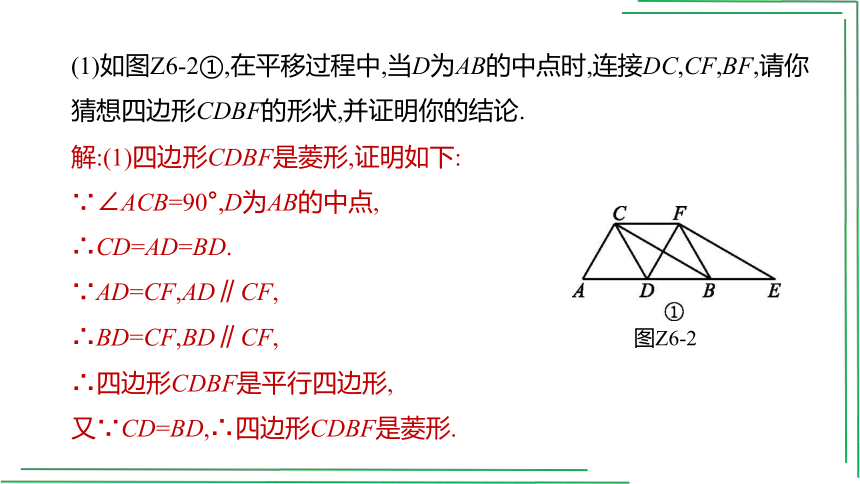
(1)如图Z6-2①,在平移过程中,当D为AB的中点时,连接DC,CF,BF,请你猜想四边形CDBF的形状,并证明你的结论.
图Z6-2
解:(1)四边形CDBF是菱形,证明如下:
∵∠ACB=90°,D为AB的中点,
∴CD=AD=BD.
∵AD=CF,AD∥CF,
∴BD=CF,BD∥CF,
∴四边形CDBF是平行四边形,
又∵CD=BD,∴四边形CDBF是菱形.
(2)如图②,在平移过程中,连接DC,CF,FB,四边形CDBF的形状在不断变化,判断它的面积变化情况,并求出其面积.
图Z6-2
(2)四边形CDBF的形状在不断改变,
但它的面积不变.
由平移的性质,得AC∥DF.
∵∠ABC=30°,AC=1,∠ACB=90°,
∴DF⊥BC,∠A=60°,BC=AC=,DF=AC=1.
∴四边形CDBF的面积为:DF×BC=×1×.
(3)在平移过程中,四边形CDBF有什么共同特征
, .(写出两个即可)
[答案] (3)(答案不唯一)CF∥BD DF⊥BC
折叠即轴对称,解决此类问题要抓住折叠的本质,从中提炼基本图形,如折叠会产生角平分线,角平分线+平行线可得等腰三角形等,进而结合图形本身的性质借助边角关系、相似等寻找解题途径.
类型二
折叠型问题
例2 如图Z6-3,已知一个直角三角形纸片ACB,其中∠ACB=90°,
AC=4,BC=3,E,F分别是AC,AB边上的点,连接EF.
(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长.
(2)如图②,若将纸片ACB的一角沿EF折叠,
折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长.
①
②
图Z6-3
(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长.
①
图Z6-3
解:(1)∵沿EF折叠后点A落在AB边上的点D处,
∴EF⊥AB,△AEF≌△DEF,
∴S△AEF=S△DEF.
∵S四边形ECBF=3S△EDF,∴S四边形ECBF=3S△AEF.
∵S△ACB=S△AEF+S四边形ECBF=4S△AEF,
∴.
∵∠EAF=∠BAC,∠AFE=∠ACB=90°,
∴△AEF∽△ABC,∴,
∴.
在Rt△ACB中,∵∠ACB=90°,AC=4,BC=3,
∴AB2=AC2+BC2,即AB==5.
∴,∴AE=.
①
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②
图Z6-3
(2)①四边形AEMF是菱形.
证明:∵折叠后点A落在BC边上的点M处,
∴∠CAB=∠EMF,AE=ME.
又∵MF∥CA,∴∠CEM=∠EMF.
∴∠CAB=∠CEM,∴ME∥AF,
∴四边形AEMF是平行四边形.而AE=ME,∴四边形AEMF是菱形.
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
②求EF的长.
②
图Z6-3
②如图,连接AM与EF交于点O,
设AE=x,则ME=x,EC=4-x,
∵∠CEM=∠CAB,∠ECM=∠ACB=90°,
∴△ECM∽△ACB,∴.
∵AB=5,AC=4,∴,解得x=,∴AE=ME=,EC=.
在Rt△ECM中,∵∠ECM=90°,
∴CM2=EM2-EC2,
即CM=,
∵四边形AEMF是菱形,
∴OE=OF,OA=OM,AM⊥EF.
∴S菱形AEMF=4S△AOE=2OE·AO.
在Rt△AOE和Rt△ACM中,
∵tan∠EAO=tan∠CAM,∴.
∵CM=,AC=4,∴AO=3OE,
∴S菱形AEMF=6OE2.
又∵S菱形AEMF=AE·CM,∴6OE2=,
∴OE=,∴EF=.
【方法点析】(1)折叠前后的图形关于折痕对称,对应点到折痕的距离相等;(2)如果翻折的是直角,那么可以构造三垂直模型,利用三角形相似解决问题;(3)如果有平行线,那么翻折后就有可能出现等腰三角形,或者角平分线;(4)如果有新的直角三角形出现,我们可以设未知数,根据勾股定理列方程求解.
例3 [2019·郴州25题改编]如图Z6-4,矩形ABCD中,点E为AB边上的动点(不与A,B重合),把△ADE沿DE翻折,点A的对应点为G,延长EG交直线DC于点F,再把∠BEF折叠,使点B的对应点T落在EF上,折痕EH交直线BC于点H.
(1)求证:△GDE∽△TEH;
(2)若AB=6,AD=4,且GT=TH,
求AE的长;
(3)如图②,若点G与点T重合,已知,求的值.
图Z6-4
(1)求证:△GDE∽△TEH;
图Z6-4
解:(1)证明:由折叠的性质可知:
∠DAE=∠DGE=90°,
∠EBH=∠ETH=90°,∠AED=∠GED,
∠BEH=∠TEH,
∴∠DEG+∠HET=90°.
又∵∠HET+∠EHT=90°,
∴∠DEG=∠EHT,∴△GDE∽△TEH.
(2)若AB=6,AD=4,且GT=TH,求AE的长;
图Z6-4
(2)连接DH,
设AE=x(0由折叠性质得:DG=AD=4,EG=x,
ET=EB=6-x,
∴TH=GT=ET-EG=(6-x)-x=6-2x,
由(1)可得:△GDE∽△TEH,∴,即,
解得x1=2,x2=12(舍去),∴AE=2.
(3)如图②,若点G与点T重合,已知,求的值.
图Z6-4
(3)设BH=4m,HC=3m(其中m>0),则AD=7m,
∵G点与T点重合,
∴由折叠性质得AE=ET=EB,DT=AD=7m,TH=BH=4m,
由(1)得△TDE∽△TEH,
∴,即TE2=TD·TH=28m2,
∴TE=2m,∴AB=AE+EB=2TE=4m,∴.
|题型精练|
1.[2021·长春]实践与探究
操作一:如图Z6-5①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则∠EAF= 度.
图Z6-5
45
操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N.我们发现,当点E的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上,则∠AEF= 度.
在图②中,运用以上操作所得结论,解答下列问题:
(1)设AM与NF的交点为点P,
求证:△ANP≌△FNE;
(2)若AB=,则线段AP的长为 .
图Z6-5
60
在图②中,运用以上操作所得结论,解答下列问题:
(1)设AM与NF的交点为点P,
求证:△ANP≌△FNE;
图Z6-5
(1)证明:由折叠可得∠FNE=∠C=90°,
∴∠ANF=∠FNE=90°.
又∵∠EAF=45°,∴∠AFN=90°-45°=45°,
∴∠EAF=∠AFN,∴AN=FN,
由折叠可知∠AMF=∠D=90°,
∴∠EFN+∠FPM=90°,
又∠NAP+∠APN=90°,∠FPM=∠APN,
∴∠NAP=∠EFN,∴△ANP≌△FNE.
在图②中,运用以上操作所得结论,解答下列问题:
(2)若AB=,则线段AP的长为 .
图Z6-5
2-2
[解析]在Rt△ABE中,∠B=90°,∠AEB=60°,
∴BE=1,又BC=AB=,
∴EC=-1,在Rt△EFC中,∠FEC=60°,
∴EF=2EC=2-2,∴AP=2-2.
2.[2020·成都]在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
(1)如图Z6-6①,若BC=2BA,求∠CBE的度数;
(2)如图②,当AB=5,且AF·FD=10时,求BC的长;
(3)如图③,延长EF,与∠ABF
的平分线交于点M,BM交AD
于点N,当NF=AN+FD时,
求的值.
图Z6-6
(1)如图Z6-6①,若BC=2BA,求∠CBE的度数;
图Z6-6
解:(1)∵将△BCE沿BE翻折,
使点C恰好落在AD边上点F处,
∴BC=BF,∠FBE=∠EBC,
∵BC=2AB,∴BF=2AB,
∴在Rt△ABF中,∠AFB=30°,
∵四边形ABCD是矩形,∴AD∥BC,∴∠AFB=∠CBF=30°,
∴∠CBE=∠FBC=15°.
(2)如图②,当AB=5,且AF·FD=10时,求BC的长;
图Z6-6
(2)∵将△BCE沿BE翻折,
使点C恰好落在AD边上点F处,
∴∠BFE=∠C=90°,CE=EF,
∴∠AFB+∠DFE=90°,
又∵矩形ABCD中,∠A=∠D=90°,
∴∠DEF+∠DFE=90°,
∴∠AFB=∠DEF,∴△FAB∽△EDF,
∴,∴AF·DF=AB·DE,
∵AF·DF=10,AB=5,∴DE=2,
∴CE=DC-DE=5-2=3,∴EF=3,
∴DF=,
∴AF==2,
∴BC=AD=AF+DF=2=3.
(3)如图③,延长EF,与∠ABF的平分线交于点M,BM交AD于点N,当NF=AN+FD时,求的值.
图Z6-6
(3)如图,过点N作NG⊥BF于点G,
∵NF=AN+FD,
∴NF=AD=BC,
∵BC=BF,∴NF=BF.
∵∠NFG=∠AFB,∠NGF=∠BAF=90°,
∴△NFG∽△BFA,
∴,
设AN=x,
∵BN平分∠ABF,AN⊥AB,NG⊥BF,
∴AN=NG=x,∴AB=2x,
易得△ABN≌△GBN,
∴AB=BG=2x.
设FG=y,则AF=2y,
在Rt△ABF中,∵AB2+AF2=BF2,
∴(2x)2+(2y)2=(2x+y)2,
解得y=x,
∴BF=BG+GF=2x+x=x,
∴.
3.[2020·淮安]【初步尝试】
(1)如图Z6-7①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
【思考说理】
(2)如图②,在三角形纸片ABC中,
AC=BC=6,AB=10,将△ABC折叠,
使点B与点C重合,折痕为MN,求的值.
图Z6-7
【拓展延伸】
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B'处,折痕为CM.
①求线段AC的长;
②若点O是边AC的中点,点P为线段OB'上
的一个动点,将△APM沿PM折叠得到△A'PM,
点A的对应点为点A',A'M与CP交于点F,
求的取值范围.
图Z6-7
(1)如图Z6-7①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
【思考说理】
(2)如图②,在三角形纸片ABC中,
AC=BC=6,AB=10,将△ABC折叠,
使点B与点C重合,折痕为MN,求的值.
图Z6-7
AM=BM
解:(2)由折叠知∠BCM=∠B.
∵AC=BC,∴∠A=∠B,∴∠BCM=∠A,
∴△BCM∽△BAC,∴,
即,∴BM=3.6,AM=6.4,
∴.
【拓展延伸】
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B'处,折痕为CM.
①求线段AC的长;
图Z6-7
(3)①由题意可知∠BCM=∠ACM=∠ACB=∠BAC,
又∠B=∠B,∴△BCM∽△BAC,
∴.
∵∠A=∠ACM,∴MA=MC,
解得MB=4,MA=MC=5,AC=7.5.
【拓展延伸】
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B'处,折痕为CM.
②若点O是边AC的中点,点P为线段OB'上
的一个动点,将△APM沿PM折叠得到△A'PM,
点A的对应点为点A',A'M与CP交于点F,
求的取值范围.
图Z6-7
②由∠A'=∠A=∠ACM,∠A'FP=∠CFM,
易得△A'PF∽△CMF,∴.
当P与B'重合时,如图①,CP=CB=6,
∴A'P=AP=7.5-6=1.5,此时;
当P与O重合时,如图②,,
∴≤≤.
4.[2019·齐齐哈尔]折纸是同学们喜欢的手工活动之一,通过折纸我们可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:如图Z6-8①,把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF.如图②,
点M为CF上一点,将正方形纸片ABCD
沿直线DM折叠,使点C落在EF上的点
N处,展开后连接DN,MN,AN.
图Z6-8
(一)填一填,做一做:
(1)图②中,∠CMD= °;
线段NF= ;
(2)图②中,试判断△AND的形状,
并给出证明.
图Z6-8
75
4-2
解:(2)△AND是等边三角形,
证明:由折叠知DN=CD,又CD=AD,∴DN=AD.
∵∠EDN=60°,∴△AND是等边三角形.
剪一剪、折一折:将图②中的△AND
剪下来,将其沿直线GH折叠,使点A
落在点A'处,分别得到图③,图④.
(二)填一填:
(3)图③中,阴影部分的周长为 ;
(4)图③中,若∠A'GN=80°,则∠A'HD= °;
(5)图③中的相似三角形(包括全等三角形)共有 对;
图Z6-8
12
40
4
(6)如图④,点A'落在边ND上,若,则= .
(用含m,n的代数式表示)
图Z6-8
(6)∵,∴设A'N=am(a>0),则A'D=an,
∵∠N=∠D=∠A=∠GA'H=60°,
∴∠NA'G+∠A'GN=∠NA'G+∠DA'H=120°,
∴∠A'GN=∠DA'H,∴△A'GN∽△HA'D,
∴,
设A'G=AG=x,A'H=AH=y,则GN=4-x,DH=4-y,
∴,
解得:,
∴.
故答案为:.
解决此类问题时,需仔细观察图形旋转前后相关的线段之间的数量关系、位置关系,相关的角的变化及角与角之间的关系,从中提炼出基本图形和常用模型,如旋转产生的等腰三角形等,进而借助全等(相似)三角形,结合勾股定理、基本图形的性质等其他知识求解.
类型三
旋转型问题
例4 [2021·成都]在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A'BC',其中点A,C的对应点分别为点A',C'.
(1)如图Z6-9①,当点A'落在AC的延长线上时,求AA'的长.
(2)如图②,当点C'落在AB的
延长线上时,连接CC',交A'B
于点M,求BM的长.
(3)如图③,连接AA',CC',直线CC'交AA'于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值 若存在,求出DE的最小值;若不存在,请说明理由.
图Z6-9
(1)如图Z6-9①,当点A'落在AC的延长线上时,求AA'的长.
图Z6-9
解:(1)∵∠ACB=90°,AB=5,BC=3,
∴AC==4.
∵∠ACB=90°,△ABC绕点B顺时针旋转
得到△A'BC',点A'落在AC的延长线上,
∴∠A'CB=90°,A'B=AB=5,
在Rt△A'BC中,A'C==4,
∴AA'=AC+A'C=8.
(2)如图②,当点C'落在AB的延长线上时,连接CC',交A'B于点M,求BM的长.
图Z6-9
(2)过C作CE∥A'B交AB于E,过C作CD⊥AB于D,如图:
∵△ABC绕点B顺时针旋转得到△A'BC',
∴∠A'BC=∠ABC,BC'=BC=3.
∵CE∥A'B,∴∠A'BC'=∠CEB,
∴∠CEB=∠ABC,∴CE=BC=3,
在Rt△ABC中,S△ABC=AC·BC=AB·CD,AC=4,BC=3,AB=5,
∴CD=.
在Rt△CED中,DE=,
同理BD=,
∴BE=DE+BD=,C'E=BC'+BE=3+.
∵CE∥A'B,∴,∴BM=.
(3)如图③,连接AA',CC',直线CC'交AA'于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值 若存在,求出DE的最小值;若不存在,请说明理由.
图Z6-9
(3)DE存在最小值1,理由如下:
过A作AP∥A'C'交C'D延长线于P,连接A'C,如图:
∵△ABC绕点B顺时针旋转得到△A'BC',
∴BC=BC',∠ACB=∠A'C'B=90°,AC=A'C',
∴∠BCC'=∠BC'C,
而∠ACP=180°-∠ACB-∠BCC'=90°-∠BCC',
∠A'C'D=∠A'C'B-∠BC'C=90°-∠BC'C,
∴∠ACP=∠A'C'D.
∵AP∥A'C',∴∠P=∠A'C'D,
∴∠P=∠ACP,∴AP=AC,∴AP=A'C',
在△APD和△A'C'D中,
∴△APD≌△A'C'D(AAS),
∴AD=A'D,即D是AA'中点.
∵点E为AC的中点,
∴DE是△AA'C的中位线,
∴DE=A'C.
要使DE最小,只需A'C最小,此时A',C,B共线,A'C的最小值为A'B-BC=AB-BC=2,∴DE最小为A'C=1.
【方法点析】共顶点的等腰三角形旋转过程中,会产生手拉手的全等三角形.图形旋转过程中三角形全等,从而得对应边相等,对应角相等,一般会得到等腰三角形,特别是旋转60°时产生等边三角形,旋转45°时产生等腰直角三角形.
|题型精练|
1.[2021·北京]如图Z6-10,在△ABC中,AB=AC,∠BAC=α,M为BC的中点,点D在MC上,以点A为中心,将线段AD顺时针旋转α得到线段AE,连接BE,DE.
(1)比较∠BAE与∠CAD的大小;用等式
表示线段BE,BM,MD之间的数量关系,并证明.
(2)过点M作AB的垂线,交DE于点N,用等式表示线段NE与ND的数量关系,并证明.
图Z6-10
(1)比较∠BAE与∠CAD的大小;用等式表示线段BE,BM,MD之间的数量关系,并证明.
图Z6-10
解:(1)∵∠DAE=∠BAC=α,
∴∠DAE-∠BAD=∠BAC-∠BAD,
即∠BAE=∠CAD.
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS),∴BE=CD,
∵M为BC的中点,∴BM=CM,∴BE+MD=BM.
(2)过点M作AB的垂线,交DE于点N,用等式表示线段NE与ND的数量关系,并证明.
图Z6-10
(2)如图,作EF⊥AB于F,交BC于H,
由(1)△ABE≌△ACD得:∠ABE=∠ACD,
∵AB=AC,∴∠ACD=∠ABC,
∴∠ABE=∠ABD,
在△BEF和△BHF中,
∴△BEF≌△BHF(ASA),∴BE=BH,
由(1)知:BE+MD=BM,∴MH=MD,
∵MN⊥AB,EF⊥AB,∴MN∥HF,
∴,∴EN=DN.
2.[2020·枣庄]在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC,BC的延长线相交,交点分别为E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图Z6-11①,若CE=CF,求证:DE=DF;
(2)如图②,在∠EDF绕点D旋转的过程中,
试证明CD2=CE·CF恒成立;
(3)如图②,若CD=2,CF=,求DN的长.
图Z6-11
(1)如图Z6-11①,若CE=CF,求证:DE=DF;
图Z6-11
解:(1)证明:∵∠ACB=90°,AC=BC,CD是中线,
∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,
∴∠DCE=∠DCF=135°.
在△DCE与△DCF中,
∴△DCE≌△DCF,∴DE=DF.
(2)如图②,在∠EDF绕点D旋转的过程中,试证明CD2=CE·CF恒成立;
图Z6-11
(2)证明:∵∠DCF=∠DCE=135°,
∴∠CDF+∠F=180°-135°=45°.
∵∠CDF+∠CDE=45°,∴∠F=∠CDE,
∴△CDF∽△CED,
∴,即CD2=CE·CF.
(3)如图②,若CD=2,CF=,求DN的长.
图Z6-11
(3)如图,过D作DG⊥BC于点G,
则∠DGN=∠ECN=90°,CG=DG.
当CD=2,CF=时,
由CD2=CE·CF,得CE=2.
在Rt△DCG中,CG=DG=
CD·sin∠DCG=2×sin45°=.
∵∠ECN=∠DGN,∠ENC=∠DNG,
∴△CEN∽△GDN.
∴=2,
∴GN=CG=,
∴DN=.
3.[2021·乐山]在等腰三角形ABC中,AB=AC,点D是BC边上一点(不与点B,C重合),连接AD.
(1)如图Z6-12①,若∠C=60°,点D关于直线AB的对称点为点E,连接AE,DE,则∠BDE= ;
(2)若∠C=60°,将线段AD绕点A顺时针
旋转60°得到线段AE,连接BE.
①在图②中补全图形;
②探究CD与BE的数量关系,并证明;
(3)如图③,若=k,且∠ADE=∠C.试探究BE,BD,AC之间满足的数量关
系,并证明.
图Z6-12
(1)如图Z6-12①,若∠C=60°,点D关于直线AB的对称点为点E,连接AE,DE,则∠BDE= ;
图Z6-12
30°
[解析]∵AB=AC,∠C=60°,
∴△ABC是等边三角形,∴∠B=60°,
∵点D关于直线AB的对称点为点E,
∴DE⊥AB,∴∠BDE=180°-60°-90°=30°.
(2)若∠C=60°,将线段AD绕点A顺时针旋转60°得到线段AE,连接BE.
①在图②中补全图形;
(2)①补全图形如下:
图Z6-12
(2)若∠C=60°,将线段AD绕点A顺时针旋转60°得到线段AE,连接BE.
②探究CD与BE的数量关系,并证明;
②CD=BE,证明如下:
∵AB=AC,∠C=60°,∴△ABC是等边三角形,
∴∠BAC=60°,
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠EAD=60°,
∴∠BAC=∠EAD,
∴∠BAC-∠BAD=∠EAD-∠BAD,
即∠EAB=∠DAC,
在△EAB和△DAC中,
∴△EAB≌△DAC(SAS),∴CD=BE.
(3)如图③,若=k,且∠ADE=∠C.试探究BE,BD,AC之间满足的数量关系,并证明.
图Z6-12
(3)AC=k(BD+BE),证明如下:
连接AE,如图:
∵AB=AC,
∴∠C=∠ABC,
∵∠ADE=∠C,∴∠ABC=∠ADE,
∵,∴△ABC∽△ADE,
∴∠DAE=∠BAC,,
∴∠DAE-∠BAD=∠BAC-∠BAD,
即∠EAB=∠DAC,
∵AB=AC,∴AE=AD,
在△EAB和△DAC中,
∴△EAB≌△DAC(SAS),∴CD=BE,
∴BC=BD+CD=BD+BE,
而=k,∴=k,
即AC=k(BD+BE).
4.[2021·龙东地区]在等腰三角形ADE中,AE=DE,△ABC是直角三角形,∠CAB
=90°,∠ABC=∠AED,连接CD,BD,点F是BD的中点,连接EF.
(1)当∠EAD=45°,点B在边AE上时,如图Z6-13①所示,求证:EF=CD.
(2)当∠EAD=45°,把△ABC绕点A逆时针旋转,顶点B落在边AD上时,如图②所示,当∠EAD=60°,点B在边AE
上时,如图③所示,猜想图
②、图③中线段EF和CD
又有怎样的数量关系.请直
接写出你的猜想,不需证明.
图Z6-13
(1)当∠EAD=45°,点B在边AE上时,如图Z6-13①所示,求证:EF=CD.
图Z6-13
解:(1)证明:∵EA=ED,∠EAD=45°,
∴∠EAD=∠EDA=45°,∴∠AED=90°,
∵BF=FD,∴EF=DB,∵∠CAB=90°,
∴∠CAD=∠BAD=45°,
∵∠ABC=∠AED=45°,∴∠ACB=∠ABC=45°,
∴AC=AB,∴AD垂直平分线段BC,∴DC=DB,∴EF=CD.
(2)当∠EAD=45°,把△ABC绕点A逆时针旋转,顶点B落在边AD上时,如图②所示,当∠EAD=60°,点B在边AE上时,如图③所示,猜想图②、图③中线段EF和CD又有怎样的数量关系.请直接写出你的猜想,不需证明.
图Z6-13
(2)题图②中,EF=CD,
题图③中,EF=CD.
5.[2020·深圳]背景:一次小组合作探究课上,小明将两个正方形按如图Z6-14所示的位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE⊥DG.
小组讨论后,提出了下列三个问题,
请你帮助解答:
(1)将正方形AEFG绕点A按逆时针
方向旋转(如图Z6-15①),还能得到
BE=DG吗 若能,请给出证明;如不能,请说明理由.
图Z6-14
图Z6-15
(2)把背景中的正方形分别改成菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转(如图Z6-15②),试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立 请说明理由.
(3)把背景中的正方形改写成矩形AEFG和矩形ABCD,且,AE=4,
AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图Z6-15③),连接DE,BG.小组发现:在旋转过程中,DE2+BG2的值是定值,请求出这个定值.
图Z6-14
图Z6-15
(1)将正方形AEFG绕点A按逆时针方向旋转(如图Z6-15①),还能得到BE=DG吗 若能,请给出证明;如不能,请说明理由.
图Z6-14
图Z6-15
解:(1)能得到BE=DG.
证明如下:∵四边形AEFG是正方形,
∴AE=AG,∠EAG=90°.
又∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠EAB=∠GAD,∴△EAB≌△GAD(SAS),
∴BE=DG.
(2)把背景中的正方形分别改成菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转(如图Z6-15②),试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立 请说明理由.
图Z6-14
图Z6-15
(2)当∠EAG=∠BAD时,BE=DG.
理由如下:∵∠EAG=∠BAD,
∴∠EAB=∠GAD.
又∵四边形AEFG和四边形ABCD均为菱形,
∴AE=AG,AB=AD,
∴△AEB≌△AGD(SAS),∴BE=DG.
(3)把背景中的正方形改写成矩形AEFG和矩形ABCD,且,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图Z6-15③),连接DE,BG.小组发现:在旋转过程中,DE2+BG2的值是定值,请求出这个定值.
图Z6-14
图Z6-15
(3)如图,连接EG,BD,设BE与DG交于点H,
∵四边形AEFG和四边形ABCD都是矩形,
∴∠EAG=∠BAD=90°,
∴∠EAB=∠GAD=90°+∠GAB.
又∵,∴△AEB∽△AGD,
∴∠EBA=∠GDA,
∵∠1=∠2,
∴∠BHD=∠BAD=90°,即BE⊥GD.
由勾股定理,得BG2+DE2=(GH2+BH2)+(EH2+DH2)=(GH2+EH2)+(BH2+DH2)=EG2+BD2,
∵,AE=4,AB=8,∴AG=6,AD=12,
∴EG2=42+62=52,BD2=82+122=208,
∴BG2+DE2=52+208=260.
例5 [2020·龙东地区28题节选]如图Z6-16,在平面直角坐标系中,矩形ABCD的边AB长是x2-3x-18=0的根,连接BD,∠DBC=30°,并过点C作CN⊥
BD,垂足为N,动点P从B点以每秒2个单位长度的速度沿BD方向匀速运动到D点为止;点M沿线段DA以每秒个单位长度的速度由点D向点A匀速运动,到点A为止,点P与点M同时出发,设运动时间为t秒(t>0).
(1)线段CN= ;
(2)连接PM和MN,求△PMN的面积S与运动
时间t的函数关系式.
类型四
动点问题
图Z6-16
3
(1)[解析]∵AB长是x2-3x-18=0的根,∴AB=6.
∵四边形ABCD是矩形,
∴AD=BC,CD=AB=6,∠BCD=90°,
又∵∠DBC=30°,
∴BD=2CD=12,BC=CD=6.
∵CN⊥BD,∴CN=BC=3,
故答案为:3.
(2)连接PM和MN,求△PMN的面积S与运动时间t的函数关系式.
图Z6-16
(2)如图,过点M作MH⊥BD于点H,
∵AD∥BC,∴∠ADB=∠DBC=30°,∴MH=MD=t.
∵∠DBC=30°,CN⊥BD,
∴BN=CN=9.
当0当t=时,点P与点N重合,S=0;
当综上所述,S=
例6 [2019·湘潭26题节选]如图Z6-17,在射线DE的一侧以AD为一条边作矩形ABCD,AD=5,CD=5,点M是线段AC上一动点(不与点A重合),连接BM,过点M作BM的垂线交射线DE于点N,连接BN.
(1)求∠CAD的大小.
(2)在动点M运动的过程中,
是否能使△AMN为等腰三
角形 如果能,求出线段MC
的长度;如果不能,请说明理由.
图Z6-17
(1)求∠CAD的大小.
图Z6-17
解:(1)∵四边形ABCD是矩形,∴∠ADC=90°.
∵tan∠DAC=,∴∠DAC=30°.
(2)在动点M运动的过程中,是否能使△AMN为等腰三角形 如果能,求出线段MC的长度;如果不能,请说明理由.
图Z6-17
(2)①如图①中,当AN=NM时,
∵∠BAN=∠BMN=90°,BN=BN,AN=NM,
∴Rt△BNA≌Rt△BNM(HL),∴BA=BM.
在Rt△ABC中,∵∠ACB=∠DAC=30°,AB=CD=5,
∴AC=2AB=10.
∵∠BAM=60°,BA=BM,
∴△ABM是等边三角形,∴AM=AB=5,
∴CM=AC-AM=5.
②如图②中,当AN=AM时,易证∠AMN=∠ANM=15°.
∵∠BMN=90°,∴∠CMB=75°,
∵∠MCB=30°,∴∠CBM=180°-75°-30°=75°,
∴∠CMB=∠CBM,∴CM=CB=5,
综上所述,满足条件的CM的值为5或5.
|题型精练|
1.[2021·南充]如图Z6-18,点E在正方形ABCD边AD上,点F是线段AB上的动点(不与点A重合),DF交AC于点G,GH⊥AD于点H,AB=1,DE=.
(1)求tan∠ACE;
(2)设AF=x,GH=y,试探究y与x的函数
关系式(写出x的取值范围);
(3)当∠ADF=∠ACE时,判断EG与AC的位置
关系并说明理由.
图Z6-18
(1)求tan∠ACE;
图Z6-18
解:(1)过点E作EM⊥AC于点M,
∴∠AME=∠EMC=90°,
∵四边形ABCD是边长为1
的正方形,DE=,
∴∠CAD=45°,AE=AD-DE=1-,
∴EM=AM=,AC=,
∴CM=AC-AM=,
∴tan∠ACE=.
(2)设AF=x,GH=y,试探究y与x的函数关系式(写出x的取值范围);
图Z6-18
(2)∵GH⊥AD,AB⊥AD,
∴GH∥AB,∴△DHG∽△DAF,
∴,∴,
∴y=x-xy,∴y=(0(3)当∠ADF=∠ACE时,判断EG与AC的位置关系并说明理由.
图Z6-18
(3)当∠ADF=∠ACE时,EG⊥AC.
理由如下:
∵∠ADF=∠ACE,
∴tan∠ADF=tan∠ACE=,
∴,∴x=,y=HG=,
∴HA=GH=,∴EH=AD-DE-AH=,
∴EH=GH,∴∠EGH=45°,
∵∠AGH=45°,
∴∠AGE=90°,
∴EG⊥AC.
2.[2021·铜仁]如图Z6-19,在△ABC中,∠ACB=90°,BC=6 cm,AC=12 cm.点P是CA边上的一动点,点P从点C出发以每秒2 cm的速度沿CA方向匀速运动,以CP为边作等边三角形CPQ(点B、点Q在AC同侧),设点P运动的时间为x秒,
△ABC与△CPQ重叠部分的面积为S.
(1)当点Q落在△ABC内部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的代数式表示,不要求写x的取值范围);
(2)当点Q落在AB上时,求此时△ABC与△CPQ重叠
部分的面积S的值;
(3)当点Q落在△ABC外部时,求此时△ABC与△CPQ
重叠部分的面积S(用含x的代数式表示).
图Z6-19
(1)当点Q落在△ABC内部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的代数式表示,不要求写x的取值范围);
图Z6-19
解:(1)过点Q作QD⊥AC于点D,如图:
∵△CPQ是等边三角形,
∴CP=CQ=2x,∠QCP=60°,
∴CD=DP=x,QD=2xsin60°
=x,
∴S=CP×QD=x2.
(2)当点Q落在AB上时,求此时△ABC与△CPQ重叠部分的面积S的值;
图Z6-19
(2)过点Q作QD⊥AC于点D,如图.
由(1)知,QD=x,CD=DP=x,则AD=12-x,
∵QD⊥AC,∠ACB=90°,
∴QD∥BC,则△AQD∽△ABC,
∴,即,解得x=4,
∴S=CP×QD=16.
(3)当点Q落在△ABC外部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的代数式表示).
图Z6-19
(3)如图,设QC,PQ分别交AB于E,F,
过点Q作QD⊥AC于点D,交AB于点G,
过点E作EM⊥AC于点M,过点F作
FN⊥AC于点N.
同(2)得CM=4,
设NP=a,则FN=a,
同理,FN∥BC,则△AFN∽△ABC,
∴,即,
∴a=12-2x,则FN=2(6-x),
∴S=S△ABC-S△EBC-S△APF=BC×AC-BC×CM-AP×FN
=×6×12-×6×4-(12-2x)·2(6-x)=24-2(6-x)2=
-2x2+24x-48.
∴△ABC与△CPQ重叠部分的面积S=-2x2+24x-48(4https://www.21cnjy.com/help/help_extract.php
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 06
几何综合型问题
●方法点析
●题型精练
●题型分类
例1 [2021·天津24题节选]在平面直角坐标系中,O为原点,△OAB是等腰直角三角形,∠OBA=90°,BO=BA,顶点A(4,0),点B在第一象限,矩形OCDE的顶点
E(-,0),点C在y轴的正半轴上,点D在第二象限,射线DC经过点B.
(1)如图Z6-1①,求点B的坐标;
(2)将矩形OCDE沿x轴向右平移,
得到矩形O'C'D'E',点O,C,D,E的
对应点分别为O',C',D',E'.设OO'=t,矩形O'C'D'E'与△OAB重叠部分的面积为S.如图②,当点E'在x轴正半轴上,且矩形O'C'D'E'与△OAB重叠部分为四边形时,
D'E'与OB相交于点F,试用含有t的式子表示S,并直接写出t的取值范围.
类型一
平移型问题
图Z6-1
(1)如图Z6-1①,求点B的坐标;
图Z6-1
解:(1)如图,过点B作BH⊥OA,垂足为H,
由点A(4,0),得OA=4,
∵BO=BA,∠OBA=90°,
∴OH=BH=OA=×4=2,
∴点B的坐标为(2,2).
(2)将矩形OCDE沿x轴向右平移,得到矩形O'C'D'E',点O,C,D,E的对应点分别为O',C',D',E'.设OO'=t,矩形O'C'D'E'与△OAB重叠部分的面积为S.如图②,当点E'在x轴正半轴上,且矩形O'C'D'E'与△OAB重叠部分为四边形时,
D'E'与OB相交于点F,试用含有t的式子
表示S,并直接写出t的取值范围.
图Z6-1
(2)由点E(-,0),得OE=,
由平移知,四边形O'C'D'E'是矩形,得∠O'E'D'=90°,O'E'=OE=,
∴OE'=OO'-O'E'=t-,∠FE'O=90°,
∵BO=BA,∠OBA=90°,
∴∠BOA=∠BAO=45°,
∴∠OFE'=90°-∠BOA=45°,
∴∠FOE'=∠OFE',∴FE'=OE'=t-,
∴S△FOE'=OE'·FE'=(t-2,
∴S=S△OAB-S△FOE'=×4×2-(t-)2,
即S=-t2+t-(4≤t<).
|题型精练|
问题情境:
小明将两个全等的Rt△ABC和Rt△DEF重叠在一起,其中∠ACB=∠DFE
=90°,∠ABC=∠DEF=30°,AC=1.固定△DEF不动,将△ABC沿直线ED向左平移,当点B与点D重合时停止移动.
猜想证明:
(1)如图Z6-2①,在平移过程中,当D为AB的
中点时,连接DC,CF,BF,请你猜想四边形
CDBF的形状,并证明你的结论.
图Z6-2
(2)如图②,在平移过程中,连接DC,CF,FB,四边形CDBF的形状在不断变化,判断它的面积变化情况,并求出其面积.
探索发现:
(3)在平移过程中,四边形CDBF有什么共同特征
, .(写出两个即可)
图Z6-2
(1)如图Z6-2①,在平移过程中,当D为AB的中点时,连接DC,CF,BF,请你猜想四边形CDBF的形状,并证明你的结论.
图Z6-2
解:(1)四边形CDBF是菱形,证明如下:
∵∠ACB=90°,D为AB的中点,
∴CD=AD=BD.
∵AD=CF,AD∥CF,
∴BD=CF,BD∥CF,
∴四边形CDBF是平行四边形,
又∵CD=BD,∴四边形CDBF是菱形.
(2)如图②,在平移过程中,连接DC,CF,FB,四边形CDBF的形状在不断变化,判断它的面积变化情况,并求出其面积.
图Z6-2
(2)四边形CDBF的形状在不断改变,
但它的面积不变.
由平移的性质,得AC∥DF.
∵∠ABC=30°,AC=1,∠ACB=90°,
∴DF⊥BC,∠A=60°,BC=AC=,DF=AC=1.
∴四边形CDBF的面积为:DF×BC=×1×.
(3)在平移过程中,四边形CDBF有什么共同特征
, .(写出两个即可)
[答案] (3)(答案不唯一)CF∥BD DF⊥BC
折叠即轴对称,解决此类问题要抓住折叠的本质,从中提炼基本图形,如折叠会产生角平分线,角平分线+平行线可得等腰三角形等,进而结合图形本身的性质借助边角关系、相似等寻找解题途径.
类型二
折叠型问题
例2 如图Z6-3,已知一个直角三角形纸片ACB,其中∠ACB=90°,
AC=4,BC=3,E,F分别是AC,AB边上的点,连接EF.
(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长.
(2)如图②,若将纸片ACB的一角沿EF折叠,
折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长.
①
②
图Z6-3
(1)如图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF,求AE的长.
①
图Z6-3
解:(1)∵沿EF折叠后点A落在AB边上的点D处,
∴EF⊥AB,△AEF≌△DEF,
∴S△AEF=S△DEF.
∵S四边形ECBF=3S△EDF,∴S四边形ECBF=3S△AEF.
∵S△ACB=S△AEF+S四边形ECBF=4S△AEF,
∴.
∵∠EAF=∠BAC,∠AFE=∠ACB=90°,
∴△AEF∽△ABC,∴,
∴.
在Rt△ACB中,∵∠ACB=90°,AC=4,BC=3,
∴AB2=AC2+BC2,即AB==5.
∴,∴AE=.
①
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②
图Z6-3
(2)①四边形AEMF是菱形.
证明:∵折叠后点A落在BC边上的点M处,
∴∠CAB=∠EMF,AE=ME.
又∵MF∥CA,∴∠CEM=∠EMF.
∴∠CAB=∠CEM,∴ME∥AF,
∴四边形AEMF是平行四边形.而AE=ME,∴四边形AEMF是菱形.
(2)如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
②求EF的长.
②
图Z6-3
②如图,连接AM与EF交于点O,
设AE=x,则ME=x,EC=4-x,
∵∠CEM=∠CAB,∠ECM=∠ACB=90°,
∴△ECM∽△ACB,∴.
∵AB=5,AC=4,∴,解得x=,∴AE=ME=,EC=.
在Rt△ECM中,∵∠ECM=90°,
∴CM2=EM2-EC2,
即CM=,
∵四边形AEMF是菱形,
∴OE=OF,OA=OM,AM⊥EF.
∴S菱形AEMF=4S△AOE=2OE·AO.
在Rt△AOE和Rt△ACM中,
∵tan∠EAO=tan∠CAM,∴.
∵CM=,AC=4,∴AO=3OE,
∴S菱形AEMF=6OE2.
又∵S菱形AEMF=AE·CM,∴6OE2=,
∴OE=,∴EF=.
【方法点析】(1)折叠前后的图形关于折痕对称,对应点到折痕的距离相等;(2)如果翻折的是直角,那么可以构造三垂直模型,利用三角形相似解决问题;(3)如果有平行线,那么翻折后就有可能出现等腰三角形,或者角平分线;(4)如果有新的直角三角形出现,我们可以设未知数,根据勾股定理列方程求解.
例3 [2019·郴州25题改编]如图Z6-4,矩形ABCD中,点E为AB边上的动点(不与A,B重合),把△ADE沿DE翻折,点A的对应点为G,延长EG交直线DC于点F,再把∠BEF折叠,使点B的对应点T落在EF上,折痕EH交直线BC于点H.
(1)求证:△GDE∽△TEH;
(2)若AB=6,AD=4,且GT=TH,
求AE的长;
(3)如图②,若点G与点T重合,已知,求的值.
图Z6-4
(1)求证:△GDE∽△TEH;
图Z6-4
解:(1)证明:由折叠的性质可知:
∠DAE=∠DGE=90°,
∠EBH=∠ETH=90°,∠AED=∠GED,
∠BEH=∠TEH,
∴∠DEG+∠HET=90°.
又∵∠HET+∠EHT=90°,
∴∠DEG=∠EHT,∴△GDE∽△TEH.
(2)若AB=6,AD=4,且GT=TH,求AE的长;
图Z6-4
(2)连接DH,
设AE=x(0
ET=EB=6-x,
∴TH=GT=ET-EG=(6-x)-x=6-2x,
由(1)可得:△GDE∽△TEH,∴,即,
解得x1=2,x2=12(舍去),∴AE=2.
(3)如图②,若点G与点T重合,已知,求的值.
图Z6-4
(3)设BH=4m,HC=3m(其中m>0),则AD=7m,
∵G点与T点重合,
∴由折叠性质得AE=ET=EB,DT=AD=7m,TH=BH=4m,
由(1)得△TDE∽△TEH,
∴,即TE2=TD·TH=28m2,
∴TE=2m,∴AB=AE+EB=2TE=4m,∴.
|题型精练|
1.[2021·长春]实践与探究
操作一:如图Z6-5①,已知正方形纸片ABCD,将正方形纸片沿过点A的直线折叠,使点B落在正方形ABCD的内部,点B的对应点为点M,折痕为AE,再将纸片沿过点A的直线折叠,使AD与AM重合,折痕为AF,则∠EAF= 度.
图Z6-5
45
操作二:如图②,将正方形纸片沿EF继续折叠,点C的对应点为点N.我们发现,当点E的位置不同时,点N的位置也不同.当点E在BC边的某一位置时,点N恰好落在折痕AE上,则∠AEF= 度.
在图②中,运用以上操作所得结论,解答下列问题:
(1)设AM与NF的交点为点P,
求证:△ANP≌△FNE;
(2)若AB=,则线段AP的长为 .
图Z6-5
60
在图②中,运用以上操作所得结论,解答下列问题:
(1)设AM与NF的交点为点P,
求证:△ANP≌△FNE;
图Z6-5
(1)证明:由折叠可得∠FNE=∠C=90°,
∴∠ANF=∠FNE=90°.
又∵∠EAF=45°,∴∠AFN=90°-45°=45°,
∴∠EAF=∠AFN,∴AN=FN,
由折叠可知∠AMF=∠D=90°,
∴∠EFN+∠FPM=90°,
又∠NAP+∠APN=90°,∠FPM=∠APN,
∴∠NAP=∠EFN,∴△ANP≌△FNE.
在图②中,运用以上操作所得结论,解答下列问题:
(2)若AB=,则线段AP的长为 .
图Z6-5
2-2
[解析]在Rt△ABE中,∠B=90°,∠AEB=60°,
∴BE=1,又BC=AB=,
∴EC=-1,在Rt△EFC中,∠FEC=60°,
∴EF=2EC=2-2,∴AP=2-2.
2.[2020·成都]在矩形ABCD的CD边上取一点E,将△BCE沿BE翻折,使点C恰好落在AD边上点F处.
(1)如图Z6-6①,若BC=2BA,求∠CBE的度数;
(2)如图②,当AB=5,且AF·FD=10时,求BC的长;
(3)如图③,延长EF,与∠ABF
的平分线交于点M,BM交AD
于点N,当NF=AN+FD时,
求的值.
图Z6-6
(1)如图Z6-6①,若BC=2BA,求∠CBE的度数;
图Z6-6
解:(1)∵将△BCE沿BE翻折,
使点C恰好落在AD边上点F处,
∴BC=BF,∠FBE=∠EBC,
∵BC=2AB,∴BF=2AB,
∴在Rt△ABF中,∠AFB=30°,
∵四边形ABCD是矩形,∴AD∥BC,∴∠AFB=∠CBF=30°,
∴∠CBE=∠FBC=15°.
(2)如图②,当AB=5,且AF·FD=10时,求BC的长;
图Z6-6
(2)∵将△BCE沿BE翻折,
使点C恰好落在AD边上点F处,
∴∠BFE=∠C=90°,CE=EF,
∴∠AFB+∠DFE=90°,
又∵矩形ABCD中,∠A=∠D=90°,
∴∠DEF+∠DFE=90°,
∴∠AFB=∠DEF,∴△FAB∽△EDF,
∴,∴AF·DF=AB·DE,
∵AF·DF=10,AB=5,∴DE=2,
∴CE=DC-DE=5-2=3,∴EF=3,
∴DF=,
∴AF==2,
∴BC=AD=AF+DF=2=3.
(3)如图③,延长EF,与∠ABF的平分线交于点M,BM交AD于点N,当NF=AN+FD时,求的值.
图Z6-6
(3)如图,过点N作NG⊥BF于点G,
∵NF=AN+FD,
∴NF=AD=BC,
∵BC=BF,∴NF=BF.
∵∠NFG=∠AFB,∠NGF=∠BAF=90°,
∴△NFG∽△BFA,
∴,
设AN=x,
∵BN平分∠ABF,AN⊥AB,NG⊥BF,
∴AN=NG=x,∴AB=2x,
易得△ABN≌△GBN,
∴AB=BG=2x.
设FG=y,则AF=2y,
在Rt△ABF中,∵AB2+AF2=BF2,
∴(2x)2+(2y)2=(2x+y)2,
解得y=x,
∴BF=BG+GF=2x+x=x,
∴.
3.[2020·淮安]【初步尝试】
(1)如图Z6-7①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
【思考说理】
(2)如图②,在三角形纸片ABC中,
AC=BC=6,AB=10,将△ABC折叠,
使点B与点C重合,折痕为MN,求的值.
图Z6-7
【拓展延伸】
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B'处,折痕为CM.
①求线段AC的长;
②若点O是边AC的中点,点P为线段OB'上
的一个动点,将△APM沿PM折叠得到△A'PM,
点A的对应点为点A',A'M与CP交于点F,
求的取值范围.
图Z6-7
(1)如图Z6-7①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为 ;
【思考说理】
(2)如图②,在三角形纸片ABC中,
AC=BC=6,AB=10,将△ABC折叠,
使点B与点C重合,折痕为MN,求的值.
图Z6-7
AM=BM
解:(2)由折叠知∠BCM=∠B.
∵AC=BC,∴∠A=∠B,∴∠BCM=∠A,
∴△BCM∽△BAC,∴,
即,∴BM=3.6,AM=6.4,
∴.
【拓展延伸】
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B'处,折痕为CM.
①求线段AC的长;
图Z6-7
(3)①由题意可知∠BCM=∠ACM=∠ACB=∠BAC,
又∠B=∠B,∴△BCM∽△BAC,
∴.
∵∠A=∠ACM,∴MA=MC,
解得MB=4,MA=MC=5,AC=7.5.
【拓展延伸】
(3)如图③,在三角形纸片ABC中,AB=9,BC=6,∠ACB=2∠A,将△ABC沿过顶点C的直线折叠,使点B落在边AC上的点B'处,折痕为CM.
②若点O是边AC的中点,点P为线段OB'上
的一个动点,将△APM沿PM折叠得到△A'PM,
点A的对应点为点A',A'M与CP交于点F,
求的取值范围.
图Z6-7
②由∠A'=∠A=∠ACM,∠A'FP=∠CFM,
易得△A'PF∽△CMF,∴.
当P与B'重合时,如图①,CP=CB=6,
∴A'P=AP=7.5-6=1.5,此时;
当P与O重合时,如图②,,
∴≤≤.
4.[2019·齐齐哈尔]折纸是同学们喜欢的手工活动之一,通过折纸我们可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
折一折:如图Z6-8①,把边长为4的正方形纸片ABCD对折,使边AB与CD重合,展开后得到折痕EF.如图②,
点M为CF上一点,将正方形纸片ABCD
沿直线DM折叠,使点C落在EF上的点
N处,展开后连接DN,MN,AN.
图Z6-8
(一)填一填,做一做:
(1)图②中,∠CMD= °;
线段NF= ;
(2)图②中,试判断△AND的形状,
并给出证明.
图Z6-8
75
4-2
解:(2)△AND是等边三角形,
证明:由折叠知DN=CD,又CD=AD,∴DN=AD.
∵∠EDN=60°,∴△AND是等边三角形.
剪一剪、折一折:将图②中的△AND
剪下来,将其沿直线GH折叠,使点A
落在点A'处,分别得到图③,图④.
(二)填一填:
(3)图③中,阴影部分的周长为 ;
(4)图③中,若∠A'GN=80°,则∠A'HD= °;
(5)图③中的相似三角形(包括全等三角形)共有 对;
图Z6-8
12
40
4
(6)如图④,点A'落在边ND上,若,则= .
(用含m,n的代数式表示)
图Z6-8
(6)∵,∴设A'N=am(a>0),则A'D=an,
∵∠N=∠D=∠A=∠GA'H=60°,
∴∠NA'G+∠A'GN=∠NA'G+∠DA'H=120°,
∴∠A'GN=∠DA'H,∴△A'GN∽△HA'D,
∴,
设A'G=AG=x,A'H=AH=y,则GN=4-x,DH=4-y,
∴,
解得:,
∴.
故答案为:.
解决此类问题时,需仔细观察图形旋转前后相关的线段之间的数量关系、位置关系,相关的角的变化及角与角之间的关系,从中提炼出基本图形和常用模型,如旋转产生的等腰三角形等,进而借助全等(相似)三角形,结合勾股定理、基本图形的性质等其他知识求解.
类型三
旋转型问题
例4 [2021·成都]在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A'BC',其中点A,C的对应点分别为点A',C'.
(1)如图Z6-9①,当点A'落在AC的延长线上时,求AA'的长.
(2)如图②,当点C'落在AB的
延长线上时,连接CC',交A'B
于点M,求BM的长.
(3)如图③,连接AA',CC',直线CC'交AA'于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值 若存在,求出DE的最小值;若不存在,请说明理由.
图Z6-9
(1)如图Z6-9①,当点A'落在AC的延长线上时,求AA'的长.
图Z6-9
解:(1)∵∠ACB=90°,AB=5,BC=3,
∴AC==4.
∵∠ACB=90°,△ABC绕点B顺时针旋转
得到△A'BC',点A'落在AC的延长线上,
∴∠A'CB=90°,A'B=AB=5,
在Rt△A'BC中,A'C==4,
∴AA'=AC+A'C=8.
(2)如图②,当点C'落在AB的延长线上时,连接CC',交A'B于点M,求BM的长.
图Z6-9
(2)过C作CE∥A'B交AB于E,过C作CD⊥AB于D,如图:
∵△ABC绕点B顺时针旋转得到△A'BC',
∴∠A'BC=∠ABC,BC'=BC=3.
∵CE∥A'B,∴∠A'BC'=∠CEB,
∴∠CEB=∠ABC,∴CE=BC=3,
在Rt△ABC中,S△ABC=AC·BC=AB·CD,AC=4,BC=3,AB=5,
∴CD=.
在Rt△CED中,DE=,
同理BD=,
∴BE=DE+BD=,C'E=BC'+BE=3+.
∵CE∥A'B,∴,∴BM=.
(3)如图③,连接AA',CC',直线CC'交AA'于点D,点E为AC的中点,连接DE.在旋转过程中,DE是否存在最小值 若存在,求出DE的最小值;若不存在,请说明理由.
图Z6-9
(3)DE存在最小值1,理由如下:
过A作AP∥A'C'交C'D延长线于P,连接A'C,如图:
∵△ABC绕点B顺时针旋转得到△A'BC',
∴BC=BC',∠ACB=∠A'C'B=90°,AC=A'C',
∴∠BCC'=∠BC'C,
而∠ACP=180°-∠ACB-∠BCC'=90°-∠BCC',
∠A'C'D=∠A'C'B-∠BC'C=90°-∠BC'C,
∴∠ACP=∠A'C'D.
∵AP∥A'C',∴∠P=∠A'C'D,
∴∠P=∠ACP,∴AP=AC,∴AP=A'C',
在△APD和△A'C'D中,
∴△APD≌△A'C'D(AAS),
∴AD=A'D,即D是AA'中点.
∵点E为AC的中点,
∴DE是△AA'C的中位线,
∴DE=A'C.
要使DE最小,只需A'C最小,此时A',C,B共线,A'C的最小值为A'B-BC=AB-BC=2,∴DE最小为A'C=1.
【方法点析】共顶点的等腰三角形旋转过程中,会产生手拉手的全等三角形.图形旋转过程中三角形全等,从而得对应边相等,对应角相等,一般会得到等腰三角形,特别是旋转60°时产生等边三角形,旋转45°时产生等腰直角三角形.
|题型精练|
1.[2021·北京]如图Z6-10,在△ABC中,AB=AC,∠BAC=α,M为BC的中点,点D在MC上,以点A为中心,将线段AD顺时针旋转α得到线段AE,连接BE,DE.
(1)比较∠BAE与∠CAD的大小;用等式
表示线段BE,BM,MD之间的数量关系,并证明.
(2)过点M作AB的垂线,交DE于点N,用等式表示线段NE与ND的数量关系,并证明.
图Z6-10
(1)比较∠BAE与∠CAD的大小;用等式表示线段BE,BM,MD之间的数量关系,并证明.
图Z6-10
解:(1)∵∠DAE=∠BAC=α,
∴∠DAE-∠BAD=∠BAC-∠BAD,
即∠BAE=∠CAD.
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS),∴BE=CD,
∵M为BC的中点,∴BM=CM,∴BE+MD=BM.
(2)过点M作AB的垂线,交DE于点N,用等式表示线段NE与ND的数量关系,并证明.
图Z6-10
(2)如图,作EF⊥AB于F,交BC于H,
由(1)△ABE≌△ACD得:∠ABE=∠ACD,
∵AB=AC,∴∠ACD=∠ABC,
∴∠ABE=∠ABD,
在△BEF和△BHF中,
∴△BEF≌△BHF(ASA),∴BE=BH,
由(1)知:BE+MD=BM,∴MH=MD,
∵MN⊥AB,EF⊥AB,∴MN∥HF,
∴,∴EN=DN.
2.[2020·枣庄]在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC,BC的延长线相交,交点分别为E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图Z6-11①,若CE=CF,求证:DE=DF;
(2)如图②,在∠EDF绕点D旋转的过程中,
试证明CD2=CE·CF恒成立;
(3)如图②,若CD=2,CF=,求DN的长.
图Z6-11
(1)如图Z6-11①,若CE=CF,求证:DE=DF;
图Z6-11
解:(1)证明:∵∠ACB=90°,AC=BC,CD是中线,
∴∠BCD=∠ACD=45°,∠BCE=∠ACF=90°,
∴∠DCE=∠DCF=135°.
在△DCE与△DCF中,
∴△DCE≌△DCF,∴DE=DF.
(2)如图②,在∠EDF绕点D旋转的过程中,试证明CD2=CE·CF恒成立;
图Z6-11
(2)证明:∵∠DCF=∠DCE=135°,
∴∠CDF+∠F=180°-135°=45°.
∵∠CDF+∠CDE=45°,∴∠F=∠CDE,
∴△CDF∽△CED,
∴,即CD2=CE·CF.
(3)如图②,若CD=2,CF=,求DN的长.
图Z6-11
(3)如图,过D作DG⊥BC于点G,
则∠DGN=∠ECN=90°,CG=DG.
当CD=2,CF=时,
由CD2=CE·CF,得CE=2.
在Rt△DCG中,CG=DG=
CD·sin∠DCG=2×sin45°=.
∵∠ECN=∠DGN,∠ENC=∠DNG,
∴△CEN∽△GDN.
∴=2,
∴GN=CG=,
∴DN=.
3.[2021·乐山]在等腰三角形ABC中,AB=AC,点D是BC边上一点(不与点B,C重合),连接AD.
(1)如图Z6-12①,若∠C=60°,点D关于直线AB的对称点为点E,连接AE,DE,则∠BDE= ;
(2)若∠C=60°,将线段AD绕点A顺时针
旋转60°得到线段AE,连接BE.
①在图②中补全图形;
②探究CD与BE的数量关系,并证明;
(3)如图③,若=k,且∠ADE=∠C.试探究BE,BD,AC之间满足的数量关
系,并证明.
图Z6-12
(1)如图Z6-12①,若∠C=60°,点D关于直线AB的对称点为点E,连接AE,DE,则∠BDE= ;
图Z6-12
30°
[解析]∵AB=AC,∠C=60°,
∴△ABC是等边三角形,∴∠B=60°,
∵点D关于直线AB的对称点为点E,
∴DE⊥AB,∴∠BDE=180°-60°-90°=30°.
(2)若∠C=60°,将线段AD绕点A顺时针旋转60°得到线段AE,连接BE.
①在图②中补全图形;
(2)①补全图形如下:
图Z6-12
(2)若∠C=60°,将线段AD绕点A顺时针旋转60°得到线段AE,连接BE.
②探究CD与BE的数量关系,并证明;
②CD=BE,证明如下:
∵AB=AC,∠C=60°,∴△ABC是等边三角形,
∴∠BAC=60°,
∵线段AD绕点A顺时针旋转60°得到线段AE,
∴AD=AE,∠EAD=60°,
∴∠BAC=∠EAD,
∴∠BAC-∠BAD=∠EAD-∠BAD,
即∠EAB=∠DAC,
在△EAB和△DAC中,
∴△EAB≌△DAC(SAS),∴CD=BE.
(3)如图③,若=k,且∠ADE=∠C.试探究BE,BD,AC之间满足的数量关系,并证明.
图Z6-12
(3)AC=k(BD+BE),证明如下:
连接AE,如图:
∵AB=AC,
∴∠C=∠ABC,
∵∠ADE=∠C,∴∠ABC=∠ADE,
∵,∴△ABC∽△ADE,
∴∠DAE=∠BAC,,
∴∠DAE-∠BAD=∠BAC-∠BAD,
即∠EAB=∠DAC,
∵AB=AC,∴AE=AD,
在△EAB和△DAC中,
∴△EAB≌△DAC(SAS),∴CD=BE,
∴BC=BD+CD=BD+BE,
而=k,∴=k,
即AC=k(BD+BE).
4.[2021·龙东地区]在等腰三角形ADE中,AE=DE,△ABC是直角三角形,∠CAB
=90°,∠ABC=∠AED,连接CD,BD,点F是BD的中点,连接EF.
(1)当∠EAD=45°,点B在边AE上时,如图Z6-13①所示,求证:EF=CD.
(2)当∠EAD=45°,把△ABC绕点A逆时针旋转,顶点B落在边AD上时,如图②所示,当∠EAD=60°,点B在边AE
上时,如图③所示,猜想图
②、图③中线段EF和CD
又有怎样的数量关系.请直
接写出你的猜想,不需证明.
图Z6-13
(1)当∠EAD=45°,点B在边AE上时,如图Z6-13①所示,求证:EF=CD.
图Z6-13
解:(1)证明:∵EA=ED,∠EAD=45°,
∴∠EAD=∠EDA=45°,∴∠AED=90°,
∵BF=FD,∴EF=DB,∵∠CAB=90°,
∴∠CAD=∠BAD=45°,
∵∠ABC=∠AED=45°,∴∠ACB=∠ABC=45°,
∴AC=AB,∴AD垂直平分线段BC,∴DC=DB,∴EF=CD.
(2)当∠EAD=45°,把△ABC绕点A逆时针旋转,顶点B落在边AD上时,如图②所示,当∠EAD=60°,点B在边AE上时,如图③所示,猜想图②、图③中线段EF和CD又有怎样的数量关系.请直接写出你的猜想,不需证明.
图Z6-13
(2)题图②中,EF=CD,
题图③中,EF=CD.
5.[2020·深圳]背景:一次小组合作探究课上,小明将两个正方形按如图Z6-14所示的位置摆放(点E,A,D在同一条直线上),发现BE=DG且BE⊥DG.
小组讨论后,提出了下列三个问题,
请你帮助解答:
(1)将正方形AEFG绕点A按逆时针
方向旋转(如图Z6-15①),还能得到
BE=DG吗 若能,请给出证明;如不能,请说明理由.
图Z6-14
图Z6-15
(2)把背景中的正方形分别改成菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转(如图Z6-15②),试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立 请说明理由.
(3)把背景中的正方形改写成矩形AEFG和矩形ABCD,且,AE=4,
AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图Z6-15③),连接DE,BG.小组发现:在旋转过程中,DE2+BG2的值是定值,请求出这个定值.
图Z6-14
图Z6-15
(1)将正方形AEFG绕点A按逆时针方向旋转(如图Z6-15①),还能得到BE=DG吗 若能,请给出证明;如不能,请说明理由.
图Z6-14
图Z6-15
解:(1)能得到BE=DG.
证明如下:∵四边形AEFG是正方形,
∴AE=AG,∠EAG=90°.
又∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠EAB=∠GAD,∴△EAB≌△GAD(SAS),
∴BE=DG.
(2)把背景中的正方形分别改成菱形AEFG和菱形ABCD,将菱形AEFG绕点A按顺时针方向旋转(如图Z6-15②),试问当∠EAG与∠BAD的大小满足怎样的关系时,背景中的结论BE=DG仍成立 请说明理由.
图Z6-14
图Z6-15
(2)当∠EAG=∠BAD时,BE=DG.
理由如下:∵∠EAG=∠BAD,
∴∠EAB=∠GAD.
又∵四边形AEFG和四边形ABCD均为菱形,
∴AE=AG,AB=AD,
∴△AEB≌△AGD(SAS),∴BE=DG.
(3)把背景中的正方形改写成矩形AEFG和矩形ABCD,且,AE=4,AB=8,将矩形AEFG绕点A按顺时针方向旋转(如图Z6-15③),连接DE,BG.小组发现:在旋转过程中,DE2+BG2的值是定值,请求出这个定值.
图Z6-14
图Z6-15
(3)如图,连接EG,BD,设BE与DG交于点H,
∵四边形AEFG和四边形ABCD都是矩形,
∴∠EAG=∠BAD=90°,
∴∠EAB=∠GAD=90°+∠GAB.
又∵,∴△AEB∽△AGD,
∴∠EBA=∠GDA,
∵∠1=∠2,
∴∠BHD=∠BAD=90°,即BE⊥GD.
由勾股定理,得BG2+DE2=(GH2+BH2)+(EH2+DH2)=(GH2+EH2)+(BH2+DH2)=EG2+BD2,
∵,AE=4,AB=8,∴AG=6,AD=12,
∴EG2=42+62=52,BD2=82+122=208,
∴BG2+DE2=52+208=260.
例5 [2020·龙东地区28题节选]如图Z6-16,在平面直角坐标系中,矩形ABCD的边AB长是x2-3x-18=0的根,连接BD,∠DBC=30°,并过点C作CN⊥
BD,垂足为N,动点P从B点以每秒2个单位长度的速度沿BD方向匀速运动到D点为止;点M沿线段DA以每秒个单位长度的速度由点D向点A匀速运动,到点A为止,点P与点M同时出发,设运动时间为t秒(t>0).
(1)线段CN= ;
(2)连接PM和MN,求△PMN的面积S与运动
时间t的函数关系式.
类型四
动点问题
图Z6-16
3
(1)[解析]∵AB长是x2-3x-18=0的根,∴AB=6.
∵四边形ABCD是矩形,
∴AD=BC,CD=AB=6,∠BCD=90°,
又∵∠DBC=30°,
∴BD=2CD=12,BC=CD=6.
∵CN⊥BD,∴CN=BC=3,
故答案为:3.
(2)连接PM和MN,求△PMN的面积S与运动时间t的函数关系式.
图Z6-16
(2)如图,过点M作MH⊥BD于点H,
∵AD∥BC,∴∠ADB=∠DBC=30°,∴MH=MD=t.
∵∠DBC=30°,CN⊥BD,
∴BN=CN=9.
当0
当
例6 [2019·湘潭26题节选]如图Z6-17,在射线DE的一侧以AD为一条边作矩形ABCD,AD=5,CD=5,点M是线段AC上一动点(不与点A重合),连接BM,过点M作BM的垂线交射线DE于点N,连接BN.
(1)求∠CAD的大小.
(2)在动点M运动的过程中,
是否能使△AMN为等腰三
角形 如果能,求出线段MC
的长度;如果不能,请说明理由.
图Z6-17
(1)求∠CAD的大小.
图Z6-17
解:(1)∵四边形ABCD是矩形,∴∠ADC=90°.
∵tan∠DAC=,∴∠DAC=30°.
(2)在动点M运动的过程中,是否能使△AMN为等腰三角形 如果能,求出线段MC的长度;如果不能,请说明理由.
图Z6-17
(2)①如图①中,当AN=NM时,
∵∠BAN=∠BMN=90°,BN=BN,AN=NM,
∴Rt△BNA≌Rt△BNM(HL),∴BA=BM.
在Rt△ABC中,∵∠ACB=∠DAC=30°,AB=CD=5,
∴AC=2AB=10.
∵∠BAM=60°,BA=BM,
∴△ABM是等边三角形,∴AM=AB=5,
∴CM=AC-AM=5.
②如图②中,当AN=AM时,易证∠AMN=∠ANM=15°.
∵∠BMN=90°,∴∠CMB=75°,
∵∠MCB=30°,∴∠CBM=180°-75°-30°=75°,
∴∠CMB=∠CBM,∴CM=CB=5,
综上所述,满足条件的CM的值为5或5.
|题型精练|
1.[2021·南充]如图Z6-18,点E在正方形ABCD边AD上,点F是线段AB上的动点(不与点A重合),DF交AC于点G,GH⊥AD于点H,AB=1,DE=.
(1)求tan∠ACE;
(2)设AF=x,GH=y,试探究y与x的函数
关系式(写出x的取值范围);
(3)当∠ADF=∠ACE时,判断EG与AC的位置
关系并说明理由.
图Z6-18
(1)求tan∠ACE;
图Z6-18
解:(1)过点E作EM⊥AC于点M,
∴∠AME=∠EMC=90°,
∵四边形ABCD是边长为1
的正方形,DE=,
∴∠CAD=45°,AE=AD-DE=1-,
∴EM=AM=,AC=,
∴CM=AC-AM=,
∴tan∠ACE=.
(2)设AF=x,GH=y,试探究y与x的函数关系式(写出x的取值范围);
图Z6-18
(2)∵GH⊥AD,AB⊥AD,
∴GH∥AB,∴△DHG∽△DAF,
∴,∴,
∴y=x-xy,∴y=(0
图Z6-18
(3)当∠ADF=∠ACE时,EG⊥AC.
理由如下:
∵∠ADF=∠ACE,
∴tan∠ADF=tan∠ACE=,
∴,∴x=,y=HG=,
∴HA=GH=,∴EH=AD-DE-AH=,
∴EH=GH,∴∠EGH=45°,
∵∠AGH=45°,
∴∠AGE=90°,
∴EG⊥AC.
2.[2021·铜仁]如图Z6-19,在△ABC中,∠ACB=90°,BC=6 cm,AC=12 cm.点P是CA边上的一动点,点P从点C出发以每秒2 cm的速度沿CA方向匀速运动,以CP为边作等边三角形CPQ(点B、点Q在AC同侧),设点P运动的时间为x秒,
△ABC与△CPQ重叠部分的面积为S.
(1)当点Q落在△ABC内部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的代数式表示,不要求写x的取值范围);
(2)当点Q落在AB上时,求此时△ABC与△CPQ重叠
部分的面积S的值;
(3)当点Q落在△ABC外部时,求此时△ABC与△CPQ
重叠部分的面积S(用含x的代数式表示).
图Z6-19
(1)当点Q落在△ABC内部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的代数式表示,不要求写x的取值范围);
图Z6-19
解:(1)过点Q作QD⊥AC于点D,如图:
∵△CPQ是等边三角形,
∴CP=CQ=2x,∠QCP=60°,
∴CD=DP=x,QD=2xsin60°
=x,
∴S=CP×QD=x2.
(2)当点Q落在AB上时,求此时△ABC与△CPQ重叠部分的面积S的值;
图Z6-19
(2)过点Q作QD⊥AC于点D,如图.
由(1)知,QD=x,CD=DP=x,则AD=12-x,
∵QD⊥AC,∠ACB=90°,
∴QD∥BC,则△AQD∽△ABC,
∴,即,解得x=4,
∴S=CP×QD=16.
(3)当点Q落在△ABC外部时,求此时△ABC与△CPQ重叠部分的面积S(用含x的代数式表示).
图Z6-19
(3)如图,设QC,PQ分别交AB于E,F,
过点Q作QD⊥AC于点D,交AB于点G,
过点E作EM⊥AC于点M,过点F作
FN⊥AC于点N.
同(2)得CM=4,
设NP=a,则FN=a,
同理,FN∥BC,则△AFN∽△ABC,
∴,即,
∴a=12-2x,则FN=2(6-x),
∴S=S△ABC-S△EBC-S△APF=BC×AC-BC×CM-AP×FN
=×6×12-×6×4-(12-2x)·2(6-x)=24-2(6-x)2=
-2x2+24x-48.
∴△ABC与△CPQ重叠部分的面积S=-2x2+24x-48(4
同课章节目录
