2022中考数学三轮冲刺专题突破07 二次函数综合问题 课件(192张)
文档属性
| 名称 | 2022中考数学三轮冲刺专题突破07 二次函数综合问题 课件(192张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:02:00 | ||
图片预览









文档简介
(共192张PPT)
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 07
二次函数综合问题
●方法点析
●题型精练
●题型分类
【基本功一】利用坐标表示线段的长
1.已知点A(0,y),B(0,1),用y表示线段AB的长:(1)若点A在点B的上方,则AB= ;
(2)若点A在点B的下方,则AB= .
类型一
二次函数与线段有关的问题
y-1
1-y
【基本功二】表示点的坐标
2.如图Z7-1,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,P是抛物线上一点,
(1)若点P的横坐标为t,则点P的坐标可
表示为 ;
(2)过点P作PH⊥x轴于点H,设点H的横
坐标为t,则点P的坐标表示为 ;
图Z7-1
(t,t2-4t+3)
(t,t2-4t+3)
(3)过点P作PQ∥y轴交直线BC于点Q,设点P的横坐标为t,则点Q的坐标表示为 ;
(4)过点P作PH⊥x轴于点H,交线段BC于点Q,当H为线段PQ的中点时,点P的坐标为 .
图Z7-1
(t,-t+3)
(2,-1)
[解析] (4)设P点的坐标为(t,t2-4t+3),
∴Q(t,3-t),所以3-t=-(t2-4t+3),解得t=2或t=3(不合题意,舍去),
∴点P的坐标为(2,-1).
【基本功三】将线段看成函数,运用函数的性质解决
3.若点P是第四象限内抛物线y=x2-4x+3上的一个动点,过点P作PQ∥y轴交直线BC于点Q,设点P的横坐标为t,PQ的长用t表
示为 ;线段PQ的最大值为 .
-t2+3t
[解析] 易知P(t,t2-4t+3),Q(t,3-t),
∴PQ=3-t-(t2-4t+3)=-t2+3t(1当t=时,PQ取得最大值为.
例1 如图Z7-2,二次函数y=x2+bx+c的图象与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C,点P是第四象限抛物线上的动点.
(1)求二次函数的解析式和直线BC的解析式;
(2)如图①,过点P作PQ⊥x轴于点Q,求PQ+QO取最大值时点P的坐标;
(3)如图②,过点P作PH⊥BC于点H,
求线段PH的最大值.
图Z7-2
(1)求二次函数的解析式和直线BC的解析式;
图Z7-2
解:(1)∵抛物线y=x2+bx+c经过A(-1,0),B(3,0),
把A,B两点坐标代入上式,得
解得
故二次函数的解析式为y=x2-2x-3,故C(0,-3).
设直线BC解析式为y=kx+m,代入B(3,0),C(0,-3),
得解得∴直线BC的解析式为y=x-3.
(2)如图①,过点P作PQ⊥x轴于点Q,求PQ+QO取最大值时点P的坐标;
图Z7-2
(2)设P(t,t2-2t-3),Q(t,0),其中0∵P在第四象限,
∴PQ+QO=-t2+2t+3+t=-t2+3t+3=-(t-)2+,
∴当t=时,PQ+QO取最大值,此时P点坐标为(,-).
(3)如图②,过点P作PH⊥BC于点H,求线段PH的最大值.
图Z7-2
(3)如图,过点P作PG∥y轴,交CB于点G,
设P(t,t2-2t-3),G(t,t-3),其中0∵OB=OC=3,且∠BOC=90°,∴∠OCB=45°,
∵PG∥y轴,∴∠PGH=∠OCB=45°,
又∵PH⊥CB,∴△PGH为等腰直角三角形,
∴PH=PG=(t-3-t2+2t+3)=(-t2+3t)=-(t-)2+,
∵0【方法点析】求一条线段的最值,可以将动点横坐标或纵坐标设为变量m,用字母m表示线段的长度L,将L看成是m的函数,求函数最值即可.求解时注意m的取值范围,用m表示线段长时注意正负号.如果不能直接表示,往往需要构建辅助线,借助特殊锐角的三角函数或者相似三角形,对线段进行转换,再求最值.
【配练】[2020·凉山州]如图Z7-3,二次函数y=ax2+bx+c的图象过
O(0,0),A(1,0),B(,)三点.
(1)求二次函数的解析式;
(2)若线段OB的垂直平分线与y轴交于点C,
与二次函数的图象在x轴上方的部分相交于
点D,求直线CD的解析式;
(3)在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
图Z7-3
(1)求二次函数的解析式;
图Z7-3
解:(1)将点O,A,B的坐标代入二次函数解析式得解得
∴二次函数的解析式为y=x2-x.
(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;
图Z7-3
(2)如图,过B作BH⊥x轴于H,连接AB,
在Rt△OBH中,
tan∠BOH=,
∴∠BOH=30°,
在Rt△AHB中,tan∠BAH=,
∴∠BAH=60°,
又∠BOA+∠OBA=∠BAH,∴∠OBA=∠BAH-∠BOH=60°-30°=30°,
∴△OBA为等腰三角形,
∴OB的垂直平分线CD必过点A(1,0),且平分∠OAB,
∴∠OAC=(180°-∠BAH)=(180°-60°)=60°,
Rt△AOC中,tan∠OAC=,
∴OC=OA·tan∠OAC=1×tan60°=,
∴C点的坐标为(0,).
设直线CD的解析式为y=kx+d,则
解得
∴直线CD的解析式为y=-x+.
(3)在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
图Z7-3
(3)如图,设点P(m,m2-m),
则点Q(m,-m+),-则PQ=-m+-(m2-m)=
-m2-m+=-(m+)2+,
∵-<0,故当m=-时,PQ有最大值,此时点P的坐标为(-,).
例2 已知抛物线y=x2-4x+3与x轴交于A,B两点(A在B点左侧),与y轴正半轴交于点C,点P是直线BC上的动点,点Q是线段OC上的动点.
(1)求∠OCB的度数.
(2)如图Z7-4①,求AQ+QP的最小值.
(3)如图②,求OP+PA的最小值,以及
此时点P的坐标.
图Z7-4
(4)如图③,AQ+QC是否存在最小值 若存在,求岀这个最小值;若不存在,请说明理由.
图Z7-4
(1)求∠OCB的度数.
解:(1)令y=0,得x2-4x+3=(x-1)(x-3)=0,
解得x=1或x=3,故A(1,0),B(3,0),
令x=0,得y=3,故C(0,3),∴OC=OB,
又∠BOC=90°,∴∠OCB=45°.
(2)如图Z7-4①,求AQ+QP的最小值.
图Z7-4
(2)如图,设点A关于y轴的对称点为A'(-1,0),则AQ+QP=A'Q+QP≥A'P,
当A',Q,P三点共线,且A'P⊥BC时,AQ+QP最短,
(理由:点线之间,垂线段最短)
Rt△A'PB中,∠OBP=90°-∠OCB=45°,
∴△A'PB是等腰直角三角形,
∴A'P=PB=A'B=2,
∴AQ+QP的最小值为2.
(3)如图②,求OP+PA的最小值,以及此时点P的坐标.
图Z7-4
(3)设点O关于直线BC的对称点为D,连接CD,PD,DB,
根据对称的性质有△OCP≌△DCP,
∴∠DCB=∠OCB=45°,
∠CDB=∠COB=90°,
CO=CD,OP=PD,∴∠OCD=90°,
∴四边形OCDB为正方形,故D(3,3),又A(1,0),
∴OP+PA=DP+PA≥DA=,
当D,P,A三点共线时取等号,(理由:两点之间,线段最短)
此时点P是直线AD:y=x-与直线BC:y=-x+3的交点,
令x-=-x+3,解得x=,
∴OP+PA的最小值为,
此时点P的坐标为(,).
(4)如图③,AQ+QC是否存在最小值 若存在,求岀这个最小值;若不存在,请说明理由.
图Z7-4
(4)如图,在x轴负半轴上找一点G,
使得∠GCO=30°,作QH⊥CG于H,
∴Rt△CQH中,HQ=QC,
∴AQ+QC=AQ+HQ≥AH,
∴当且仅当A,Q,H三点共线,且AH⊥CG时取等号,(理由:点线之间,垂线段最短)
在Rt△COG中,∠GCO=30°,CO=3,
∴GO=CO·tan30°=,
当AH⊥GC时,在Rt△AGH中,
∠HGA=60°,AG=1+,
∴AH=AG·sin60°=,∴AQ+QC的最小值为.
【方法点析】求线段和的最值,一般需要通过对称变换后,通过等量代换,利用“两点之间线段最短”或“点线之间,垂线段最短”求得最值.其变式问题有三角形或四边形的周长最小等.
【配练】[2021·通辽26题节选]如图Z7-5,抛物线y=ax2+bx+3交x轴于A(3,0),B(-1,0)两点,交y轴于点C,动点P在抛物线的对称轴上.
(1)求抛物线的解析式.
(2)当以P,B,C为顶点的三角形周长最小时,
求点P的坐标及△PBC的周长.
图Z7-5
(1)求抛物线的解析式.
图Z7-5
解:(1)将A(3,0),B(-1,0)分别代入y=ax2+bx+3,
得解得:
∴抛物线的解析式为y=-x2+2x+3.
(2)当以P,B,C为顶点的三角形周长最小时,求点P的坐标及△PBC的周长.
图Z7-5
(2)由题意可得,抛物线的对称轴为直线x=-=1.
如图,连接AC交直线x=1于点P, 连接PB,PC,BC.
∵点A与点B关于直线x=1对称,
∴PA=PB,∴PB+PC+BC=PA+PC+BC.
当A,P,C三点共线时,PA+PC的值最小,
即△PBC的周长最小.
设直线AC的解析式为y=kx+h,将A(3,0),C(0,3)分别代入,得
解得
∴直线AC的解析式为y=-x+3,
当x=1时,y=-1+3=2,∴P(1,2).
∵AC==3,BC=,
∴△PBC周长的最小值=PB+PC+BC=AC+BC=+3.
|题型精练|
1.[2021·荆门24题节选]如图Z7-6,抛物线y=ax2+bx+c交x轴于A(-1,0),B(3,0)两点,交y轴于点C(0,-3),点Q为线段BC上的动点.
(1)求抛物线的解析式;
(2)求QO+QA的最小值.
图Z7-6
(1)求抛物线的解析式;
图Z7-6
解:(1)∵抛物线经过A,B两点,
∴设解析式为y=a(x+1)(x-3).
将C(0,-3)代入求得a=1.
∴抛物线的解析式为y=(x+1)(x-3),
即y=x2-2x-3.
(2)求QO+QA的最小值.
图Z7-6
(2)如图,∵OB=OC=3,∠BOC=90°,
∴△OBC是等腰直角三角形.
∴点O(0,0)关于BC的对称点O'
的坐标为(3,-3).
连接AO'交BC于点Q',连接OQ',则当点Q与点Q'重合时,
QO+QA的值最小,
最小值=Q'O+Q'A=Q'O'+Q'A=AO'==5.
2.如图Z7-7,抛物线L:y=x2-x-3与x轴正半轴交于点A,与y轴交于点B.
(1)求直线AB的解析式及抛物线顶点坐标;
(2)点P为第四象限且在对称轴右侧抛物线
上一动点,过点P作PC⊥x轴,垂足为C,PC交
AB于点D,求PD+BD的最大值,并求出此时
点P的坐标.
图Z7-7
(1)求直线AB的解析式及抛物线顶点坐标;
图Z7-7
解:(1)在y=x2-x-3中,令y=0,
则x2-x-3=0.
解得x1=-,x2=4.∴A(4,0).
令x=0,得y=-3,∴B(0,-3).
设直线AB的解析式为y=kx+b,
则解得
∴直线AB的解析式为y=x-3.
∵y=x2-x-3=(x-)2-,
∴抛物线顶点坐标为(,-).
(2)点P为第四象限且在对称轴右侧抛物线
上一动点,过点P作PC⊥x轴,垂足为C,PC交
AB于点D,求PD+BD的最大值,并求出此时
点P的坐标.
图Z7-7
(2)∵OA=4,OB=3,∴AB==5.
设点P的坐标为(x,x2-x-3)(则OC=x,点D的坐标为(x,x-3).
∵PC⊥x轴,∴PC∥y轴.∴,即.∴BD=x.
∵PD=x-3-(x2-x-3)=-x2+2x.
∴PD+BD=-x2+2x+x=-x2+x=-(x-)2+.
∵-<0,当x=时,PD+BD的最大值为.
此时y=()2-=-.∴P(,-).
例3 如图Z7-8,已知抛物线y=-x2-2x+3与x轴负半轴交于点A,与y轴交于点B,顶点为C.
(1)求△ABC的面积;
(2)若点P是抛物线上点A与点B之间的
动点(不包括点A,点B),求△PAB的面积的
最大值,并求出此时点P的坐标;
(3)若点Q是抛物线上的点(不与点C重合),横坐标为m,且S△ABQ=S△ABC,求m的值.
类型二
二次函数与图形面积问题
图Z7-8
(1)求△ABC的面积;
图Z7-8
解:(1)由抛物线的解析式y=-x2-2x+3
可得A(-3,0),B(0,3).
顶点C的坐标为(-1,4),
易求得直线AB的解析式为y=x+3,
如图①,设抛物线对称轴与直线AB交于点D,
则D点坐标为(-1,2),故CD=2,
∴S△ABC=S△ACD+S△BCD=×CD×|xA-xB|=3.
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标;
图Z7-8
(2)如图②,作PM∥y轴,交直线AB于点M,
设P(x,-x2-2x+3),则M(x,x+3),
∴PM=-x2-2x+3-(x+3)=-x2-3x,
∴S△PAB=(-x2-3x)×3=-(x+)2+.
当x=-时,S△PAB最大=,此时yP=-(-)2-2×(-)+3=,
∴△PAB的面积的最大值为,此时点P的坐标为(-,).
(3)若点Q是抛物线上的点(不与点C重合),横坐标为m,且S△ABQ=S△ABC,求m的值.
图Z7-8
(3)[方法一]如图③,过点Q作QN∥y轴,交直线AB于点N,
依题有Q(m,-m2-2m+3),N(m,m+3),
∴QN=|yN-yQ|=|m+3+m2+2m-3|=|m2+3m|,
又S△ABC=3,
∴S△ABQ=×QN×|xA-xB|=
|m2+3m|=3,
当m2+3m>0时,m2+3m=2,
解得m1=,m2=,
当m2+3m<0时,m2+3m=-2,
解得m3=-1(舍去),m4=-2.
综上,符合要求的Q点横坐标m为-2或或.
[方法二]如图④,
①若Q在直线AB上方,过点C作CQ∥AB,
与抛物线的另一个交点为Q,
∵CQ∥AB,即有平行线之间距离处处相等,
且同底AB,
∴S△ABQ=S△ABC,
此时直线CQ的解析式为y=x+5,与y轴交点坐标为(0,5),
令x+5=-x2-2x+3,解得x1=-1(舍去),x2=-2.
②若Q在直线AB的下方,将①中直线CQ向下平移2个单位得到直线AB,再向下平移2个单位得到直线l:y=x+1,直线l与抛物线的交点即为所求,
令x+1=-x2-2x+3,解得x3=,x4=.
综上,符合要求的Q点横坐标m为-2
或或.
【方法点析】如图Z7-9,求由两个定点A,B和动点P组成的△ABP的面积,可过点P作y轴的平行线,交直线AB于点Q,则S△ABP=PQ×|xA-xB|.
图Z7-9
【配练】如图Z7-10,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作
QE∥AC,交BC于点E,连接CQ.当
△CQE的面积最大时,求点Q的坐标.
图Z7-10
(1)求该抛物线的解析式;
图Z7-10
解:(1)由题意,得
解得
∴该抛物线的解析式为:y=-x2+x+4.
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标.
图Z7-10
(2)设点Q的坐标为(m,0),过点E作EG⊥x轴于点G.
由-x2+x+4=0,得x1=-2,x2=4,
∴点B的坐标为(-2,0),∴AB=6,BQ=m+2,
∵QE∥AC,∴△BQE∽△BAC,
∴,即,∴EG=,
∴S△CQE=S△CBQ-S△EBQ=BQ·CO-BQ·EG=(m+2)(4-)=
-m2+m+=-(m-1)2+3,
又∵-2≤m≤4,
∴当m=1时,S△CQE有最大值3,此时Q(1,0).
例4 [2018·日照21题改编]如图Z7-11①,已知点A(-1,0),B(3,0),
C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线的解析式及顶点D的坐标;
图Z7-11
(2)如图②,连接CD,AC,BD,求四边形ACDB和△CBD的面积;
(3)如图③,在直线BC上方的抛物线上求一点N,使△NBC面积为1;
图Z7-11
(4)如图④,点E是直线BC上方的抛物线上一点,过点E作x轴的垂线,垂足为F,求△BEF的面积被直线CB平分时点E的坐标.
图Z7-11
(1)求抛物线的解析式及顶点D的坐标;
图Z7-11
解:(1)把A(-1,0),B(3,0),C(0,1)分别代入y=ax2+bx+c,
得解得
所以抛物线的解析式为y=-x2+x+1.
因为y=-x2+x+1=-(x2-2x-3)=-[(x-1)2-4]=-(x-1)2+,
所以D点坐标为(1,).
(2)如图②,连接CD,AC,BD,求四边形ACDB和△CBD的面积;
图Z7-11
(2)OA=1,OB=3,OC=1,DM=,OM=1,BM=2,
S四边形ACDB=S△AOC+S梯形COMD+S△BDM
=×1×1+×(1+)×1+×2×=3.
S△CBD=S四边形ACDB-S△ABC=3-×4×1=1.
(3)如图③,在直线BC上方的抛物线上求一点N,使△NBC面积为1;
图Z7-11
(3)∵B(3,0),C(0,1),
∴直线BC的解析式为y=-x+1,
作NF⊥x轴,交直线BC于H,交x轴于F,
设N(x,-x2+x+1),易得H(x,-x+1).
∴NH=-x2+x+1-(-x+1)=-x2+x.
∴S△NBC=S△NHC+S△NHB=NH(xB-xC)=(-x2+x)·(3-0)=-x2+x.
∵S△NBC=1,∴-x2+x=1,
∴x2-3x+2=0,解得x1=1,x2=2.
∴N1(1,),N2(2,1).
(4)如图④,点E是直线BC上方的抛物线上一点,过点E作x轴的垂线,垂足为F,求△BEF的面积被直线CB平分时点E的坐标.
图Z7-11
(4)设E点坐标为(m,-m2+m+1),直线EF
交BC于点H,当△BEF的面积被直线CB
平分时,EH=HF.所以点H的坐标为
(m,-m2+m+).
因为直线BC的解析式为y=-x+1,
所以点H的坐标为(m,-m+1),所以-m2+m+=-m+1,解得m1=1,m2=3,
m=3不合题意,舍去.
∴当m=1时,△BEF的面积被直线CB平分,此时点E的坐标为(1,),即顶点D.
|题型精练|
1.如图Z7-12,抛物线y=ax2+bx-3与x轴交于点A(-1,0),B,与y轴交于点C,且过点D(2,-3).点P是抛物线上的一个动点.
(1)求抛物线的表达式;
(2)当点P在第四象限运动时,
求四边形ACPB的最大面积.
图Z7-12
(1)求抛物线的表达式;
图Z7-12
解:(1)∵抛物线y=ax2+bx-3经过
点A(-1,0),D(2,-3),
∴解得
∴抛物线的表达式为y=x2-2x-3.
(2)当点P在第四象限运动时,求四边形ACPB的最大面积.
图Z7-12
(2)∵抛物线y=x2-2x-3与y轴交于点C,
∴C(0,-3),CO=3.
令y=0,得x2-2x-3=0,解得x1=-1,x2=3,
∴点B(3,0),OB=3.
连接BC,∵点A(-1,0),∴AB=4,
∴S△ABC=AB·CO=×4×3=6.
∵S四边形ACPB=S△ACB+S△PBC,
∴当△PBC的面积最大时,四边形ACPB的面积最大.
如图,过点P作PQ平行于y轴,交BC于点Q.
由B(3,0),C(0,-3)可知直线BC的表达式为
y=x-3.
设P(m,m2-2m-3)(0∴PQ=m-3-(m2-2m-3)=-m2+3m=-(m-)2+,
S△PBC=PQ·OB=[-(m-)2+]×3
=-(m-)2+.
∵-<0,∴当m=时,△PBC的面积最大,最大值为.
∵6+,
∴四边形ACPB的面积的最大值为.
2.[2021·荆门24题改编]如图Z7-13,抛物线y=x2-2x-3交x轴于A,B两点,交y轴于C,点Q为线段BC上的动点.过点Q作PQ∥AC交抛物线的第四象限部分于点P,连接PA,PB,记△PAQ与△PBQ的面积分别为S1,S2,设S=S1+S2,求点P坐标,
使得S最大,并求此最大值.
图Z7-13
解:由题意得A(-1,0),B(3,0),C(0,-3),过点P作PE⊥x轴于点E,交BC于点D,连接PC.
∵B(3,0),C(0,-3),∴直线BC的解析式为y=x-3.
设点P的横坐标为m,则PE=-(m2-2m-3),
DE=-(m-3),
PD=PE-DE=-(m2-2m-3)+(m-3)=-m2+3m.
∵PQ∥AC,S1=S△PAQ=S△PCQ.
∴S=S1+S2=S△PCQ+S△PBQ=S△PBC=PD·OB=(-m2+3m)=-(m-)2+,
∴当m=时,S最大,最大值=.
当m=时,y=()2-2×-3=-,
∴点P的坐标为(,-),S的最大值为.
3.[2020·重庆B卷25题节选]如图Z7-14,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)与y轴交于点C,与x轴交于A,B两点(点A在点B的左侧),且A点坐标为(-,0),直线BC的解析式为y=-x+2.
(1)求抛物线的解析式.
(2)过点A作AD∥BC,交抛物线于点D,
点E为直线BC上方抛物线上一动点,
连接CE,BE,BD,DC.求四边形BECD
面积的最大值及相应点E的坐标.
图Z7-14
(1)求抛物线的解析式.
图Z7-14
解:(1)直线BC的解析式为y=-x+2,
当y=0时,x=3,则点B(3,0).
将A(-,0),B(3,0)代入y=ax2+bx+2中,得
解得
∴抛物线的解析式为y=-x2+x+2.
(2)过点A作AD∥BC,交抛物线于点D,点E为直线BC上方抛物线上一动点,连接CE,BE,BD,DC.求四边形BECD
面积的最大值及相应点E的坐标.
图Z7-14
(2)连接AC.∵AD∥CB,
∴S△BCD=S△ABC=×4×2=4.
∴S四边形BECD=S△BCD+S△BCE=4+S△BCE.
过点E作EF∥y轴,交直线BC于点F.
设点E(m,-m2+m+2),则F(m,-m+2),
∴EF=-m2+m+2-(-m+2)=-m2+m.
∴S△BCE=OB·EF=×3×(-m2+m)=-m2+3m=-(m-)2+.
∵-<0,∴当m=时,S△BCE取得最大值,最大值为,此时点E(,),
∴当点E的坐标为(,)时,四边形BECD面积的最大值为+4.
角度1 等腰三角形存在性问题
例5 已知在平面直角坐标系中,点A的坐标为(3,1),请在x轴上找一点P,使△AOP为等腰三角形,则符合条件的点P的坐标为
.
类型三
二次函数与特殊三角形存在性问题
(-,0),(,0),(,0),(6,0)
[解析]方法一(几何法):
①OA=OP时,如图①所示,P1,P3即为所求.
∵OA=,∴OP=,∴点P坐标为(-,0),(,0);
②AO=AP时,如图①所示,P4即为所求,点P坐标为(6,0);
③当PO=PA时,如图①所示,P2即为所求,
如图②,作AB⊥x轴于点B,连接AP2,
设OP2=AP2=x,则BP2=3-x,在Rt△AP2B中,
由勾股定理可知x2=(3-x)2+12,
解得x=,即点P坐标为.
综上所述,点P的坐标为(-,0),,(,0),(6,0).
方法二(代数法):
设点P的坐标为(x,0),易得OA=,OP=|x|,AP= .
①当AO=OP时,=|x|,解得x=±,
此时点P的坐标为(-,0),(,0);
②当AO=AP时,,解得x=0(舍去)或x=6,此时点P的坐标为(6,0);
③当OP=PA时,|x|=,解得x=,此时点P的坐标为.
综上所述,点P的坐标为(-,0),(,0),(,0),(6,0).
【方法点析】求解等腰三角形的存在性问题有两种基本方法:
(1)代数法:适用于三角形的边长容易由勾股定理求解的情况.步骤如下:
①根据点的坐标,表示出AB2,BC2,CA2;
②根据等腰三角形的性质,可得到三个方程:
AB2=BC2,BC2=CA2,CA2=AB2;
③分别解这三个方程,若能得到方程有解,则这个解即为所求;若方程无解,则不存在这样的三角形.
(2)几何法(两圆一线):
①满足条件的点C在如图Z7-15所示的分别以点A,B为圆心,以线段AB长为半径的圆上或在线段AB的垂直平分线上(除去与AB在一条直线上的点).
②利用勾股定理、相似、三角函数等求线段长,得出点的坐标.
图Z7-15
例6 如图Z7-16,已知抛物线y=-x2-4x+12与x轴交于点A,B(A在B的左侧),与y轴交于点C.
(1)x轴上是否存在点F,使得△BCF是以BC
为底边的等腰三角形 若存在,求出点F的
坐标;若不存在,说明理由.
图Z7-16
(2)x轴上是否存在点M,使得△BCM是以BC为腰的等腰三角形 若存在,求出点M的坐标;若不存在,说明理由.
(3)在抛物线的对称轴上是否存在点G,使得△BCG为等腰三角形 若存在,求出点G的坐标;若不存在,说明理由.
图Z7-16
(4)设抛物线的顶点为D,点P在抛物线上,点H在抛物线的对称轴上,是否存在点P使得△PDH是等边三角形 若存在,求出P点的坐标;若不存在,说明理由.
图Z7-16
(1)x轴上是否存在点F,使得△BCF是以BC为底边的等腰三角形 若存在,求出点F的坐标;若不存在,说明理由.
图Z7-16
解:(1)令x=0,则y=12,
令y=0,则-x2-4x+12=0,解得x1=-6,x2=2.
∴A(-6,0),B(2,0),C(0,12).
设点F的坐标为(t,0).
由已知得OC=12,FB=2-t,FC=
,
∵△BCF是以BC为底边的等腰三角形,
∴FB=FC,即2-t=,解得t=-35.
∴点F的坐标为(-35,0).
(2)x轴上是否存在点M,使得△BCM是以BC为腰的等腰三角形 若存在,求出点M的坐标;若不存在,说明理由.
图Z7-16
(2)∵B(2,0),C(0,12),
∴利用勾股定理可得BC==2.
因为△BCM是以BC为腰的等腰三角形,所以分两种情况:
①BM=BC时,M1(2-2,0),M2(2+2,0);
②CM=CB时,M3(-2,0).
综上所述,当M的坐标为(2-2,0)或(2+2,0)或
(-2,0)时,△BCM是以BC为腰的等腰三角形.
(3)在抛物线的对称轴上是否存在点G,使得△BCG为等腰三角形 若存在,求出点G的坐标;若不存在,说明理由.
图Z7-16
(3)由(2)得BC=2.设点G(-2,n),
△BCG为等腰三角形分三种情况:
①当CG=CB时,CG=.
∵CG=CB,∴=2,
解得n1=0,n2=24(不合题意,舍去),
故G的坐标为(-2,0).
②当BC=BG时,BG=,
∵BC=BG,∴=2,
解得n3=2,n4=-2.
因此点G的坐标为(-2,2)或(-2,-2).
③当BG=CG时,GC=,GB=,
∵GC=GB,∴,解得n=5.5,故点G坐标为
(-2,5.5).
综上所述,当G的坐标为(-2,0)或(-2,2)或(-2,-2)或(-2,5.5)时,
△BCG为等腰三角形.
(4)设抛物线的顶点为D,点P在抛物线上,点H在抛物线的对称轴上,是否存在点P使得△PDH是等边三角形 若存在,求出P点的坐标;若不存在,说明理由.
图Z7-16
(4)设点P(m,-m2-4m+12),过点P作PN
垂直于抛物线的对称轴,垂足为N,
∵y=-x2-4x+12=-(x+2)2+16,
∴D(-2,16).
由于△PDH是等边三角形,由等边三角形的性质得PN=ND,而PN=|m-(-2)|=|m+2|,ND=16-(-m2-4m+12)=(m+2)2,
由PN=ND,得|m+2|=(m+2)2,
解得m1=-2,m2=--2,m3=-2(不合题意,舍去).
因此P点的坐标是(-2,)或(--2,).
角度2 直角三角形存在性问题
例7 如图Z7-17,已知直线y=kx-6经过点A(1,-4),与x轴相交于点B,若点Q是y轴上一点,且△ABQ为直角三角形,则点Q的坐标
为 .
图Z7-17
(0,-)或(0,)或(0,-1)或(0,-3)
[解析]方法一:将(1,-4)代入y=kx-6中,解得k=2,
∴直线解析式为y=2x-6,∴B(3,0).
设直线AB交y轴于点C,则C(0,-6),由题意知AB2=20,
设Q(0,y).
①当∠QAB=90°时,AQ2+AB2=BQ2.
∵AQ2=CQ2-AC2=(y+6)2-5=y2+12y+31,BQ2=OQ2+OB2=y2+9,
∴y2+12y+31+20=y2+9,
解得y=-,∴Q(0,-).
②当∠QBA=90°时,AB2+BQ2=AQ2.
∵AQ2=y2+8y+17,BQ2=y2+9,∴20+y2+9=y2+8y+17,
解得y=,∴Q(0,).
③当∠AQB=90°时,AQ2+BQ2=AB2.
∵AQ2=y2+8y+17,BQ2=y2+9,∴y2+8y+17+y2+9=20,
解得y=-1或y=-3,
∴Q(0,-1)或Q(0,-3).
综上,Q点的坐标为(0,-),(0,),(0,-1)或(0,-3).
方法二:设直线AB与y轴交于点D,
易得D(0,-6),B(3,0),AD=,BD=3.
①如图①,当∠Q1AB=90°时,
∵∠Q1AD=∠DOB=90°,∠Q1DA=∠ODB,
∴△DAQ1∽△DOB,
∴,即,∴DQ1=,
∴OQ1=,即Q1(0,-);
②如图②,当∠Q2BA=90°时,
∵∠Q2OB=∠BOD,∠Q2BO=∠ODB,
∴△BOQ2∽△DOB,
∴,即,
∴OQ2=,即Q2(0,);
③如图③,以AB为直径画圆与y轴分别交于点Q3,Q4,作AE⊥y轴,垂足为点E,
易得△AEQ3∽△Q3OB,
∴,即,
解得OQ3=1或OQ3=3,
∴Q3(0,-3),Q4(0,-1).
综上,Q1(0,-),Q2(0,),Q3(0,-3),Q4(0,-1).
【方法点析】求解直角三角形的存在性问题的常用方法有两种:
(1)代数法:设出一个点的坐标,表示出AB2,BC2,CA2,
分三种情况:①AB2=BC2+CA2;②BC2=CA2+AB2;
③CA2=AB2+BC2,根据不同的情况建立方程求解.
(2)几何法:
①两线一圆作出点:如图Z7-18,满足条件的点C在如图所示的分别过点A,B且垂直AB的直线上或在以线段AB为直径的圆上(除去与AB在一条直线上的点).
②构造相似(常需要构造一线三等角相似),利用对应边成比例求线段长,进而求得点的坐标.
图Z7-18
例8 如图Z7-19,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(-1,0)两点,与y轴交于点C.
(1)求这条抛物线对应的函数表达式.
(2)问在y轴上是否存在点P,使得△PAM为直角三角形 若存在,求出点P的坐标;若不存在,说明理由.
(3)设点H是第一象限内抛物线上的动点,
点Q是线段AC上的一点,是否存在点H,Q
使得△HCQ是等腰直角三角形 若存在,
求出点Q的坐标;若不存在,请说明理由.
图Z7-19
(1)求这条抛物线对应的函数表达式.
图Z7-19
解:(1)将A,B两点坐标代入抛物线表达式,
得解得
∴y=-x2+2x+3.
(2)问在y轴上是否存在点P,使得△PAM为直角三角形 若存在,求出点P的坐标;若不存在,说明理由.
图Z7-19
(2)方法一:存在点P,使△PAM是直角三角形.
∵y=-x2+2x+3=-(x-1)2+4,∴M(1,4).
如图①,当点M为直角顶点时,
过M作EF⊥y轴于点E,过A作
AF⊥EF于点F.
∵∠AMP=90°,
∴∠EMP+∠AMF=90°,易知∠F=90°,
∴∠AMF+∠MAF=90°,∴∠EMP=∠MAF.
又∵∠AFM=∠PEM,∴△EPM∽△FMA,
∴,∴,∴PE=,∴P(0,).
如图②,当点A为直角顶点时,过A作EF⊥x轴,
过M作MF⊥AF于F,过P作PE⊥AE于点E,
同上可证△EPA∽△FAM,∴,
∴,∴AE=,∴P(0,-).
如图③,当点P为直角顶点时,过M作ME⊥y轴于E,
∴△EPM∽△OAP,∴,∴,解得PE=1或3,
∴P(0,3)或(0,1).
综上所述,使△PAM是直角三角形的
点P的坐标是(0,),(0,-),(0,3),(0,1).
方法二:存在点P使得△PAM是直角三角形.
易得M(1,4),A(3,0),设P(0,m).
∴AP2=(3-0)2+(0-m)2=m2+9,AM2=(3-1)2+(0-4)2=20,
MP2=(1-0)2+(4-m)2=m2-8m+17.
当∠APM=90°时,AP2+MP2=AM2,
即m2+9+m2-8m+17=20,
∴m1=1,m2=3.∴P1(0,1),P2(0,3).
当∠PAM=90°时,AP2+AM2=MP2,
即m2+9+20=m2-8m+17,∴m=-,∴P3(0,-).
当∠PMA=90°时,MP2+AM2=AP2,
即m2-8m+17+20=m2+9,∴m=,∴P4(0,).
综上,点P的坐标为(0,1)或(0,3)或(0,-)或(0,).
(3)设点H是第一象限内抛物线上的动点,
点Q是线段AC上的一点,是否存在点H,Q
使得△HCQ是等腰直角三角形 若存在,
求出点Q的坐标;若不存在,请说明理由.
图Z7-19
(3)存在点H,Q,使△HCQ是等腰直角三角形.
①如图,当∠HCQ=90°时,要使Rt△HCQ为
等腰直角三角形,则有∠CQH=45°,HC=QC.
∵△OAC为等腰直角三角形,
∴∠OCA=∠OAC=45°.∴QH∥y轴.
设H(n,-n2+2n+3),则Q(n,-n+3),
则HC2=n4-4n3+5n2,QC2=2n2,
∴n4-4n3+5n2=2n2,
解得n=0(舍去)或1或3(舍去),∴H(1,4),Q(1,2).
②当∠CHQ=90°时,CH∥x轴,HQ∥y轴,此时∠QCH=∠CQH=45°,△CHQ为等腰直角三角形.
由图象易得点C与点H关于对称轴对称,∴H(2,3),Q(2,1).
③当∠CQH=90°时,∠QCH=∠CHQ=45°,
∴CH∥x轴,
如图,过点Q作QT⊥CH,垂足为T.
∵△CHQ是等腰直角三角形,QT⊥CH,
∴CT=HT,∴Q在对称轴上,
∴Q(1,2).
综上,点Q的坐标为(1,2)或(2,1).
|题型精练|
1.[2020·无锡]二次函数y=ax2-3ax+3的图象过点A(6,0),且与y轴交于点B,点M在该抛物线的对称轴上,若△ABM是以AB为直角
边的直角三角形,则点M的坐标为 .
(,-9)或(,6)
[解析]把点A(6,0)代入y=ax2-3ax+3,得0=36a-18a+3,
解得:a=-,∴y=-x2+x+3,
∴B(0,3),抛物线的对称轴为直线x=-.
设点M的坐标为(,m),
当∠ABM=90°时,过B作BD⊥对称轴于D,如图,
则∠1=∠2,∴tan∠2=tan∠1==2,
∴=2,∴DM=3,∴M(,6).
当∠M'AB=90°时,∠1=∠3,
∴tan∠3==tan∠1==2,∴M'N=9,∴M'(,-9).
综上所述,点M的坐标为(,-9)或(,6).
2.[2021·湖州]已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线y=ax2+bx+2(a≠0)对称轴上的一个动点.小明经探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定,若抛物线y=ax2+bx+2
(a≠0)的对称轴上存在3个不同的点M,使△AOM为直角三角形,则的值是 .
2或-8
[解析] ∵△AOM是直角三角形,
∴一定存在两个以A,O为直角顶点的直角
三角形,且点M在对称轴上的直角三角形,
∴当以OA为直径的圆与抛物线的对称轴
x=-相切时,对称轴上存在1个以M为直角顶点的直角三角形,此时对称轴上存在3个不同的点M,使△AOM为直角三角形(如图所示).
易知,-=-1或4,∴=2或-8,故答案为:2或-8.
3.[2020·徐州28题节选]如图Z7-20,在平面直角坐标系中,函数y=-ax2+
2ax+3a(a>0)的图象交x轴于点A,B,交y轴于点C,它的对称轴交x轴于点E.过点C作CD∥x轴交抛物线于点D,连接DE并延长交y轴于点F,交抛物线于点G.直线AF交CD于点H,交抛物线于点K,连接HE,GK.
(1)点E的坐标为: ;
(2)当△HEF是直角三角形时,求a的值.
图Z7-20
(1,0)
[解析]对于抛物线y=-ax2+2ax+3a,它的对称轴为直线x=-=1,
∴E点的坐标为(1,0).
(2)当△HEF是直角三角形时,求a的值.
图Z7-20
(2)对于抛物线y=-ax2+2ax+3a,
令y=0,有-ax2+2ax+3a=0,解得x1=-1,x2=3,
∴A点的坐标为(-1,0),B点的坐标为(3,0),
令x=0,则y=3a,∴点C的坐标为(0,3a),
由于CD∥x轴,∴点D和点C关于抛物线的对称轴对称,
∴点D的坐标为(2,3a),
设直线DE的解析式为y=kx+b,代入(1,0)和(2,3a),
有解得∴直线ED的解析式为y=3ax-3a,
令x=0,则y=-3a,
∴点F的坐标为(0,-3a),
解方程组得G的坐标为(-3,-12a),
同理可求得直线HK的解析式为:y=-3ax-3a,点K的坐标为(6,-21a),
对于直线y=-3ax-3a,令y=3a,解得H的坐标为(-2,3a),
∴H(-2,3a),E(1,0),F(0,-3a),
∴HE2=9a2+9,HF2=36a2+4,EF2=9a2+1,
当HE2=HF2+EF2时,有9a2+9=36a2+4+9a2+1,
解得a=(舍负),
当HF2=HE2+EF2时,有36a2+4=9a2+9+9a2+1,
解得a=(舍负),
当EF2=HE2+HF2时,有9a2+1=9a2+9+36a2+4,无解,
∴a的值为或.
4.[2021·宿迁28题节选]如图Z7-21,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(4,0),与y轴交于点C.连接AC,BC,点P在抛物线上运动.若点P在第一象限,直线AP交BC于
点F,过点P作x轴的垂线交BC于点H,
当△PFH为等腰三角形时,求线段PH
的长.
图Z7-21
解:将A(-1,0),B(4,0)代入y=-x2+bx+c中,可解得b=,c=2,
∴y=-x2+x+2,令x=0,得y=2,∴C(0,2),
由B(4,0),C(0,2)得直线BC的解析式为y=-x+2.
设PH与x轴的交点为N,P(a,-a2+a+2),则H(a,-a+2),PH=-a2+2a,
若FP=FH,则∠FPH=∠FHP=∠BHN=∠BCO,
∴tan∠APN=tan∠BCO=2,∴AN=2PN,
即a+1=2(-a2+a+2),
解得a=3或a=-1(舍去),此时PH=.
若PF=PH,过点F作FM⊥y轴于点M.
由题意知AB=5,AC=,BC==2,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠ACB=90°,
易知∠PFH=∠PHF,
∵∠CFA=∠PFH,∠NHB=∠PHF,
∴∠CFA=∠NHB,
又∵∠ACF=∠BNH=90°,
∴△ACF∽△BNH,∴∠CAF=∠NBH,
∴,∴CF=AC=.
∵FM⊥y轴,∴FM∥OB,
∴∠CPM=∠CBO,∴,
在Rt△CMF中,由CF=,得MF=1,CM=,∴F(1,),
∴直线AF的解析式为y=x+,
联立抛物线解析式得x+=-x2+x+2,
解得x=或x=-1(舍去),此时PH=.
若HF=HP,过点C作CE∥AB交AP于点E,
∵∠CAF+∠CFA=90°,∠PAN+∠HPF=90°,
∠CFA=∠HFP=∠HPF,
∴∠CAF=∠PAN,即AP平分∠CAB,
∴CE=CA=,∴E(,2),
∴直线AE的解析式为:y=x+,
联立抛物线解析式得x+=-x2+x+2,
解得x=5-或x=-1(舍去).
此时PH=3-5.
综上,线段PH的长为或3-5或.
5.[2021·随州24题节选]在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于点A和点B,与y轴交于点C,如图Z7-22,M是直线BC上一个动点,过点M作MN⊥x轴交抛物线于点N,Q是直线AC上一个动点,当△QMN为等腰直角三角形
时,求此时点M及其对应点Q的坐标.
图Z7-22
解:抛物线y=x2-2x-3与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C(0,-3),设直线AC解析式为y=m1x+n1,直线BC解析式为y=m2x+n2,
∵A(-1,0),C(0,-3),∴
解得∴直线AC解析式为y=-3x-3.
∵B(3,0),C(0,-3),∴解得
∴直线BC解析式为y=x-3.
设M(t,t-3),则N(t,t2-2t-3),
∴MN=|t2-2t-3-(t-3)|=|t2-3t|,
①当△QMN是以NQ为斜边的等腰直角三角形时,此时∠NMQ=90°,MN=MQ,如图①,
②当△QMN是以MQ为斜边的等腰直角三角形时,此时∠MNQ=90°,MN=NQ,如图②,
③当△QMN是以MN为斜边的等腰直角三角形时,此时∠MQN=90°,MQ=NQ,如图③,
综上所述,点M及其对应点Q的坐标为:M1(,),Q1(-,);M2(,-) ,
Q2(-,-);M3(5,2),Q3(-5,12);M4(2,-1),Q4(0,-3);M5(7,4),Q5(-7,18);
M6(1,-2),Q6(0,-3).
例9 如图Z7-23,在平面直角坐标系中,已知点A(-3,4),B(-6,-2),
C(6,-2),若以点A,B,C,D为顶点作平行四边形,则点D的坐标为
.
类型四
二次函数与特殊四边形存在性问题
图Z7-23
(-15,4)或(3,-8)或(9,4)
【方法点析】已知三定点,探求第四个点,使之构成平行四边形,构图方法:作平行线.
如图Z7-24,根据平行四边形的性质,分别过三个定点A,B,C作各自对边的平行线,三条平行线的交点即为点D的位置.
图Z7-24
例10 如图Z7-25,已知抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式.
(2)设抛物线的对称轴为l,与x轴的交点为D.
在直线l上是否存在点M,使得四边形CDPM
是平行四边形 若存在,求出点M的坐标;若
不存在,请说明理由.
图Z7-25
(3)变式1:如图Z7-26,点N在x轴上,点Q在抛物线上,若以点C,D,N,Q为顶点的四边形是平行四边形,求出所有点N的坐标.
(4)变式2:如图Z7-27,点E是线段OB上的动点,过点E作x轴的垂线l',交抛物线于点F,在抛物线上是否存在点T,使四边形CETF是矩形 若存在,求出E点坐标;若不存在,请说明理由.
图Z7-26
图Z7-27
(1)求抛物线的表达式.
图Z7-25
解:(1)∵抛物线y=-x2+bx+c经过
A(-1,0),B(3,0)两点,
∴抛物线的表达式为y=-(x+1)(x-3),
即y=-x2+2x+3.
(2)设抛物线的对称轴为l,与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形 若存在,求出点M的坐标;若不存在,请说明理由.
图Z7-25
(2)如图,连接PC,设PC交抛物线对称轴l:直线x=1于点H,
当CP与DM互相平分时,四边形CDPM是平行四边形,
此时H为CP的中点,H为DM的中点,
∴=xH,而xC=0,xH=1,
∴xP=2,故点P(2,3),又C(0,3),
∴H(1,3),MH=HD=3,
∴M(1,6).
(3)变式1:如图Z7-26,点N在x轴上,点Q在抛物线上,若以点C,D,
N,Q为顶点的四边形是平行四边形,求出所有点N的坐标.
图Z7-26
(3)变式1:依题设N(n,0),Q(m,-m2+2m+3),
①CD为对角线时,CD与QN互相平分,
则
解得(舍去)
或此时Q(2,3),N(-1,0).
②CQ为对角线时,CQ与DN互相平分,
则
解得或
此时Q(1+,-3),N(,0)或Q(1-,-3),N(-,0).
③DQ为对角线时,DQ与CN互相平分,
则
解得(舍去)或
此时Q(2,3),N(3,0).
综上,符合要求的点N的坐标为
(-1,0),(,0),(-,0),(3,0).
(4)变式2:如图Z7-27,点E是线段OB上的动点,过点E作x轴的垂线l',交抛物线于点F,在抛物线上是否存在点T,使四边形CETF是矩形 若存在,求出E点坐标;若不存在,请说明理由.
图Z7-27
变式2:不存在点T,使四边形CETF是矩形.理由:假设存在点F,则当∠ECF=90°,且CT与EF互相平分时,四边形CETF为矩形,
设E(a,0),则F(a,-a2+2a+3),其中0则
解得
故T(2a,-a2+2a),
将T点坐标代入抛物线解析式得-4a2+4a+3=-a2+2a,
化简,得3a2-2a-3=0,
解得a1=,a2=(舍去).
另一方面,若∠ECF=90°,则有CF2+CE2=EF2,
即a2+(-a2+2a)2+a2+32=(-a2+2a+3)2=(-a2+2a)2+6(-a2+2a)+32,
解得a3=0(舍去),a4=,
由a1≠a4说明不存在a的值同时满足条件:∠ECF=90°,CT与EF互相平分,∴抛物线上不存在点T,使四边形CETF是矩形.
【方法点析】(1)对于两个定点,两个动点的问题,一般思路是先用一个未知数表示相对简单的那个动点的坐标,将这三个点看成定点,用该未知数表示另一个动点的坐标,再根据条件求相应点的坐标.
(2)矩形存在问题可以转化为直角三角形存在问题;菱形存在问题可以转化为等腰三角形存在问题;正方形存在问题可以转化为等腰直角三角形存在问题.
|题型精练|
1.如图Z7-28,抛物线y=-x2+2x+3交x轴于A,B两点,交y轴于点C,动点P在抛物线的对称轴上.若点Q是平面直角坐标系内的任意一点,是否存在点Q,使得以A,C,P,Q
为顶点的四边形是菱形 若存在,求出
所有符合条件的点Q的坐标;若不存在,
请说明理由.
图Z7-28
解:令y=0,则-x2+2x+3=0,解得x1=-1,x2=3,
∴A(3,0),B(-1,0).
令x=0,则y=3,∴C(0,3).
设P(1,t),①以AC为边时,如图①,
∵四边形ACPQ是菱形,∴CP=CA,
∴12+(3-t)2=32+32,解得:t=3±,
∴P1(1,3-),P2(1,3+),
∴Q1(4,-),Q2(4,).
如图②,∵四边形ACQP是菱形,∴AC=AP,
∴(3-1)2+t2=32+32,解得t=±.
∴P3(1,),P4(1,-),
∴Q3(-2,3+),Q4(-2,3-).
②以AC为对角线时,如图③,
∵四边形APCQ是菱形,∴CP=PA,
∴12+(3-t)2=(1-3)2+t2,
解得:t=1,∴P5(1,1),Q5(2,2),
综上所述,符合条件的点Q的坐标为:(4,-)或(4,)或
(-2,3+)或(-2,3-)或(2,2).
2.如图Z7-29,在平面直角坐标系中,抛物线y=-x2+2x+与x轴交于点A,B,与y轴交于点C,连接BC,点D为此抛物线的顶点.点P在抛物线对称轴上,平面内存在点Q,使以点B,C,P,Q为顶点的四边形为矩形,求点Q的坐标.
图Z7-29
解:令y=0,则-x2+2x+=0,解得x=-1或x=5.
∴A(-1,0),B(5,0),
令x=0,则y=,∴C(0,),易知对称轴为直线x=2.
设P(2,y),Q(m,n),
①若BC为矩形的对角线,
则解得:
又∵∠BPC=90°,∴PC2+PB2=BC2,
即:22+(-y)2+32+y2=52+()2,
解得y=4或y=-,∴n=-或n=4,
∴Q(3,-)或Q(3,4).
②若BP为矩形的对角线,则解得
又∵∠BCP=90°,∴BC2+CP2=BP2,
即:52+()2+22+(-y)2=32+y2,解得y=,∴Q(7,4).
③若BQ为矩形的对角线,则解得:
又∵∠BCQ=90°,∴BC2+CQ2=BQ2,
即:52+()2+m2+(-n)2=(5-m)2+n2,
解得n=-,∴Q(-3,-),
综上所述,点Q的坐标为(3,-)或(3,4)或(7,4)或(-3,-).
例11 [2020·怀化24题改编]如图Z7-30所示,抛物线y=x2-2x-3与x轴相交于A,B两点,与y轴相交于点C,点M为抛物线的顶点.
(1)求点C及顶点M的坐标.
(2)连接AC,BM,CM,BC,判断△BCM和
△AOC是否相似 请说明理由.
(3)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P,E,O为顶点的三角形与△ABC相似 若存在,求出点P的坐标;若不存在,请说明理由.
类型五
二次函数与相似三角形存在性问题
图Z7-30
(1)求点C及顶点M的坐标.
图Z7-30
解:(1)将x=0代入y=x2-2x-3,得y=-3,故点C的坐标为(0,-3),
又∵y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点M的坐标为(1,-4).
(2)连接AC,BM,CM,BC,判断△BCM和△AOC是否相似 请说明理由.
图Z7-30
(2)相似.理由如下:
令y=x2-2x-3=0,解得:x=3或x=-1,
∴B(3,0),A(-1,0),
∴BC==3,CM=,BM=2,
又AC=,∴,
∴△AOC∽△MCB.
(3)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P,E,O为顶点的三角形与△ABC相似 若存在,求出点P的坐标;若不存在,请说明理由.
图Z7-30
(3)点P的坐标为(-,-)或(-1,2),
连接OP,如图所示.
∵C(0,-3),M(1,-4),
∴直线MC的解析式为:y=-x-3,
将y=0代入直线MC的解析式得E点坐标为(-3,0),
∴OE=OB=3,且OC⊥BE,∴CE=CB,∴∠CBE=∠CEB,
设P(x,-x-3),
又∵P点在线段EM上,∴-3则EP=(x+3),BC==3,
由题意知:△PEO与△ABC相似,分两种情况讨论:
①当△PEO∽△CBA时,
有,∴,
解得x=-,满足-3②当△PEO∽△ABC时,有,∴,
解得x=-1,满足-3综上所述,P点的坐标为(-,-)或(-1,-2).
【方法点析】相似三角形存在问题,往往需要先确定一组对应角相等,然后利用这组角的夹边对应成比例即可列式求解,夹边的对应需要分成两类讨论.或者利用等角的三角函数列方程.如果等角不能确定,那么就需要对角进行讨论,注意三角形中的特殊角,包括已知三角函数值的角.
|题型精练|
1.[2021·陕西]已知抛物线y=-x2+2x+8与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求点B,C的坐标.
(2)设点C'与点C关于该抛物线的对称轴对称.在y轴上是否存在点P,使△PCC'与△POB相似,且PC与PO是对应边 若存在,求出点P的坐标;若不存在,请说明理由.
(1)求点B,C的坐标.
解:(1)∵y=-x2+2x+8,令x=0,得y=8,
∴C(0,8),
令y=0,得-x2+2x+8=0,
解得:x1=-2,x2=4,∴B(4,0).
(2)设点C'与点C关于该抛物线的对称轴对称.在y轴上是否存在点P,使△PCC'与△POB相似,且PC与PO是对应边 若存在,求出点P的坐标;若不存在,请说明理由.
(2)存在,由已知得,该抛物线的对称轴为直线x=1,
∵点C'与点C关于直线x=1对称,
∴C'(2,8),CC'=2.∴CC'∥OB.
∵点P在y轴上,∴∠PCC'=∠POB=90°,
∴当时,△PCC'∽△POB.设P(0,y),
当y>8时,则,∴y=16.∴P(0,16).
当0当y<0时,则CP>OP,与矛盾.
∴点P不存在.
∴P(0,16)或P(0,).
2.[2021·无锡27题节选]在平面直角坐标系中,O为坐标原点,直线y=-x+3与x轴交于点B,与y轴交于点C(如图Z7-31),二次函数y=ax2+2x+c的图象过B,C两点,且与x轴交于另一点A,点M为线段OB上的一个动点,过点M作直线l平行于y轴交BC于点F,交二次函数y=ax2+2x+c的图象于点E.
(1)求二次函数的表达式;
(2)当以C,E,F为顶点的三角形与
△ABC相似时,求线段EF的长度.
图Z7-31
(1)求二次函数的表达式;
图Z7-31
解:(1)∵直线y=-x+3,∴B(3,0),C(0,3),
把B,C坐标代入抛物线y=ax2+2x+c,
得解得
∴二次函数的表达式为y=-x2+2x+3.
(2)当以C,E,F为顶点的三角形与△ABC相似时,求线段EF的长度.
图Z7-31
(2)根据题意画图如图,
令y=0,则-x2+2x+3=0,解得x1=-1,x2=3,
∴A(-1,0),∴AB=4,BC=3.
∵OB=OC,∴∠OBC=45°,
∵FM⊥OB,∴∠CFE=∠MFB=45°,
∴∠CFE=∠ABC.
设E(m,-m2+2m+3),则F(m,-m+3),
∴EF=-m2+3m,CF=m.
①当时,△ABC∽△CFE,
∴,
解得m1=0(舍去),m2=,
∴EF=-m2+3m=;
②当时,△ABC∽△EFC,
∴,
解得m1=0(舍去),m2=,∴EF=-m2+3m=;
综上所述,EF=或.
例12 [2020·张家界23题改编]如图Z7-32,抛物线y=ax2-6x+c交x轴于A,B两点,交y轴于点C,直线y=-x+5经过点B,C.
(1)求抛物线的解析式及∠ACB的正切值.
(2)点P是抛物线上的动点,当∠PAB=∠ACB时,求点P的坐标.
(3)在直线BC上是否存在点M,使AM与直线BC的
夹角等于∠ACB的2倍 若存在,请求出点M的坐标;
若不存在,请说明理由.
类型六
二次函数与角度的结合问题
图Z7-32
(1)求抛物线的解析式及∠ACB的正切值.
图Z7-32
解:(1)∵直线y=-x+5经过点B,C,
∴C(0,5),B(5,0),将B,C坐标分别代入y=ax2-6x+c,
得解得
∴该抛物线的解析式为y=x2-6x+5,
如图①,过点A作直线BC的垂线,
垂足为H,
令x2-6x+5=0,解得x=1或x=5,故A(1,0),又∵C(0,5),B(5,0),
∴BC==5,AB=4,OC=5,AC=,
∴S△ABC=×AB×OC=×BC×AH,即4×5=5×AH,解得AH=2,
在Rt△AHC中,由勾股定理得:
CH==3,
∴tan∠ACB=.
(2)点P是抛物线上的动点,当∠PAB=∠ACB时,求点P的坐标.
图Z7-32
(2)如图①,作PG⊥x轴于点G,设G(m,0),
P(m,m2-6m+5),
在Rt△APG中,tan∠PAB=,
又∵∠PAB=∠ACB,
∴=|m-5|,解得m=或m=,∴P点坐标为(,)或(,-).
(3)在直线BC上是否存在点M,使AM与直线BC的夹角等于∠ACB的2倍 若存在,请求出点M的坐标;若不存在,请说明理由.
图Z7-32
(3)存在.理由如下:如图②,作线段AC的
垂直平分线交直线BC于点M1,
∴M1C=M1A,
∴∠ACM1=∠CAM1=∠AM1B,
即∠AM1B=2∠ACB,
∵直线BC的解析式为y=-x+5,
∴设M1(t,-t+5),又∵A(1,0),
∴由A=C得(t-1)2+(-t+5)2=t2+(-t+5-5)2,
解得t=,
∴M1坐标为(,).
作点M1关于点H的对称点M2,有AM1=AM2,故∠AM2C=∠AM1B=2∠ACB,
设M2(s,-s+5),又∵A(1,0),
∴由A=A得(-1)2+()2=(s-1)2+(-s+5)2,解得s=或s=,∴M2坐标为(,).
综上,M点坐标为(,)或(,).
【方法点析】等角条件时,可以先求出已知角的正切值,然后根据函数解析式设元,构造直角三角形,利用正切值列方程.倍角条件时,需要借助辅助线转换为等角条件,常用的辅助线有构造平行线,或者构造等腰三角形,构造辅助圆等.
|题型精练|
[2019·咸宁24题节选]如图Z7-33,在平面直角坐标系中,直线y=
-x+2与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过A,B两点且与x轴的负半轴交于点C.
(1)求该抛物线的解析式;
(2)若点D为直线AB上方抛物线上的一个动点,
当∠ABD=2∠BAC时,求点D的坐标.
图Z7-33
(1)求该抛物线的解析式;
图Z7-33
解:(1)在y=-x+2中,令y=0,得x=4,令x=0,得y=2,
∴A(4,0),B(0,2),代入y=-x2+bx+c
得解得
∴抛物线的解析式为y=-x2+x+2.
(2)若点D为直线AB上方抛物线上的一个动点,当∠ABD=
2∠BAC时,求点D的坐标.
图Z7-33
(2)如图,过点B作x轴的平行线交抛物线于点E,过点D作BE的垂线,垂足为F,
∵BE∥x轴,∴∠BAC=∠ABE,
∵∠ABD=2∠BAC,∴∠ABD=2∠ABE,
即∠DBE+∠ABE=2∠ABE,
∴∠DBE=∠ABE,∴∠DBE=∠BAC,
设D点的坐标为,则BF=x,DF=-x2+x,
∵tan∠DBE=,tan∠BAC=,
∴,即,
解得x1=0(舍去),x2=2,
当x=2时,-x2+x+2=3,
∴点D的坐标为(2,3).
例13 已知抛物线y=ax2+bx+c(a≠0)的顶点坐标是(2,1),并且经过点(4,2).直线y=x+1与抛物线交于B,D两点.
(1)求抛物线的解析式.
(2)以BD为直径作圆,圆心为点C,
求证:圆C与x轴相切.
类型七
二次函数与圆的结合问题
图Z7-34
(3)圆C与直线m交于抛物线的对称轴右侧的点M(t,1).直线m上每一点的纵坐标都等于1.过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F.求BE∶MF的值.
图Z7-34
(1)求抛物线的解析式.
图Z7-34
解:(1)设抛物线的解析式为y=a(x-h)2+k,
∵抛物线的顶点坐标是(2,1),
∴y=a(x-2)2+1,
又∵抛物线经过点(4,2),
∴2=a(4-2)2+1,
解得a=,
∴抛物线的解析式是y=(x-2)2+1=x2-x+2.
(2)以BD为直径作圆,圆心为点C,求证:圆C与x轴相切.
图Z7-34
(2)证明:解方程组
得
得到点B的坐标为(3-,),点D的坐标为(3+,).
∵点C是BD的中点,
∴点C的纵坐标为,
利用两点间距离公式,可算出BD==5.
∴圆C的半径r=,
∴圆心C到x轴的距离等于半径r,∴圆C与x轴相切.
(3)圆C与直线m交于抛物线的对称轴右侧的点M(t,1).直线m上每一点的纵坐标都等于1.过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F.求BE∶MF的值.
图Z7-34
(3)方法一:连接BM和DM,
∵BD为直径,∴∠BMD=90°,
∴∠BME+∠DMF=180°-90°=90°,
又∵BE⊥直线m于点E,DF⊥直线m于点F,
∴∠DMF+∠MDF=90°,
∴∠BME=∠MDF,∴△BME∽△MDF,
∴,
∵BE=,MF=3+-t,EM=t-(3-),DF=,
∴,
化简得(t-3)2=4,解得t=5或t=1,
抛物线的对称轴为直线x=2,
∵点M在对称轴右侧,∴t=5,∴.
方法二:如图,过点C作CH⊥直线m,垂足为H,连接CM,
由(2)知CM=r=,CH=r-1=,
在Rt△CHF中,由勾股定理,得MH==2,
又∵HF=,
∴MF=HF-MH=-2,
又∵BE=-1=,∴.
【方法点析】与圆有关的切线问题,可以转化为切点到圆心距离等于半径,或者转化为直角三角形问题,或者构造K字形找相似三角形来列方程.与圆有关的角度问题,可以考虑圆心角、圆周角的性质定理进行角度转换.
|题型精练|
[2021·张家界23题节选]如图Z7-35,已知二次函数y=ax2+bx+c的图象经过点C(2,-3),且与x轴交于原点及点B(8,0).
(1)求二次函数的表达式;
(2)求顶点A的坐标及直线AB的表达式;
(3)若点P为☉O上的动点,且☉O的半径为2,
一动点E从点A出发,以每秒2个单位长度的速度沿线段AP匀速运动到点P,再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动,求点E的运动时间t的最小值.
图Z7-35
(1)求二次函数的表达式;
图Z7-35
解:(1)根据题意得
解得
∴抛物线的解析式为y=x2-2x.
(2)求顶点A的坐标及直线AB的表达式;
图Z7-35
(2)∵y=x2-2x=(x2-8x+16-16)=(x-4)2-4,
∴二次函数图象的顶点A的坐标为(4,-4).
设直线AB的解析式为y=mx+n.
则有解得
∴直线AB的解析式为y=x-8.
(3)若点P为☉O上的动点,且☉O的半径为2,一动点E从点A出发,以每秒2个单位长度的速度沿线段AP匀速运动到点P,再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动,求点E的运动时间t的最小值.
图Z7-35
(3)如图,点P在以O为圆心,2为半径的圆周上.
依题意可知:动点E的运动时间t=AP+BP.
在OA上取Q使OQ=,连接PQ,PO.
∵OA==4,OP=2,∴,
∵∠POQ=∠AOP,∴△OQP∽△OPA,
∴,∴t=AP+BP=PQ+BP.
显然当B,P,Q三点共线时,PQ+BP取得最小值BQ.
过点Q作QH⊥OB于H.易得OA=AB=4,OB=8,
∴OA2+AB2=OB2,∴∠OAB=90°,
∴△ABO为等腰直角三角形,
∴∠AOB=45°,∴在Rt△OQH中,QH=OH=1,
∴BH=OB-OH=7,
∴BQ==5,
∴t的最小值为5.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2022中考数学三轮冲刺专题突破
中考专区
2022年中考数学三轮复习(人教版)
专题突破 07
二次函数综合问题
●方法点析
●题型精练
●题型分类
【基本功一】利用坐标表示线段的长
1.已知点A(0,y),B(0,1),用y表示线段AB的长:(1)若点A在点B的上方,则AB= ;
(2)若点A在点B的下方,则AB= .
类型一
二次函数与线段有关的问题
y-1
1-y
【基本功二】表示点的坐标
2.如图Z7-1,抛物线y=x2-4x+3与x轴交于A,B两点,与y轴交于点C,P是抛物线上一点,
(1)若点P的横坐标为t,则点P的坐标可
表示为 ;
(2)过点P作PH⊥x轴于点H,设点H的横
坐标为t,则点P的坐标表示为 ;
图Z7-1
(t,t2-4t+3)
(t,t2-4t+3)
(3)过点P作PQ∥y轴交直线BC于点Q,设点P的横坐标为t,则点Q的坐标表示为 ;
(4)过点P作PH⊥x轴于点H,交线段BC于点Q,当H为线段PQ的中点时,点P的坐标为 .
图Z7-1
(t,-t+3)
(2,-1)
[解析] (4)设P点的坐标为(t,t2-4t+3),
∴Q(t,3-t),所以3-t=-(t2-4t+3),解得t=2或t=3(不合题意,舍去),
∴点P的坐标为(2,-1).
【基本功三】将线段看成函数,运用函数的性质解决
3.若点P是第四象限内抛物线y=x2-4x+3上的一个动点,过点P作PQ∥y轴交直线BC于点Q,设点P的横坐标为t,PQ的长用t表
示为 ;线段PQ的最大值为 .
-t2+3t
[解析] 易知P(t,t2-4t+3),Q(t,3-t),
∴PQ=3-t-(t2-4t+3)=-t2+3t(1
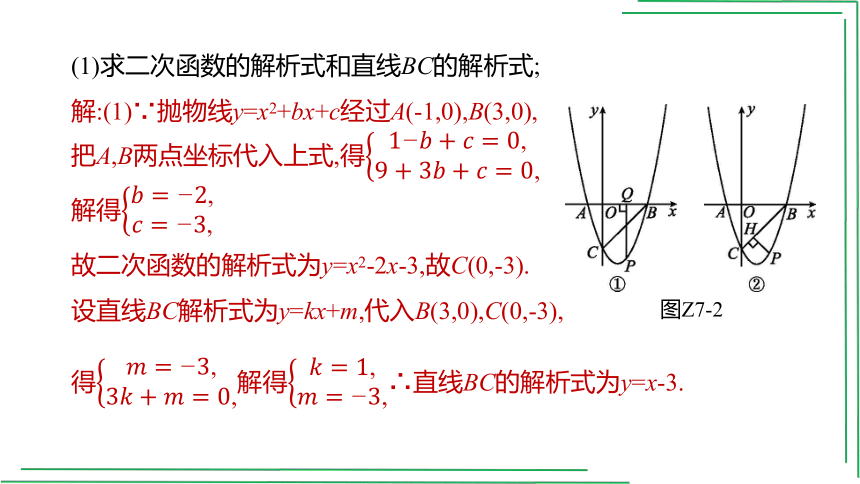
例1 如图Z7-2,二次函数y=x2+bx+c的图象与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C,点P是第四象限抛物线上的动点.
(1)求二次函数的解析式和直线BC的解析式;
(2)如图①,过点P作PQ⊥x轴于点Q,求PQ+QO取最大值时点P的坐标;
(3)如图②,过点P作PH⊥BC于点H,
求线段PH的最大值.
图Z7-2
(1)求二次函数的解析式和直线BC的解析式;
图Z7-2
解:(1)∵抛物线y=x2+bx+c经过A(-1,0),B(3,0),
把A,B两点坐标代入上式,得
解得
故二次函数的解析式为y=x2-2x-3,故C(0,-3).
设直线BC解析式为y=kx+m,代入B(3,0),C(0,-3),
得解得∴直线BC的解析式为y=x-3.
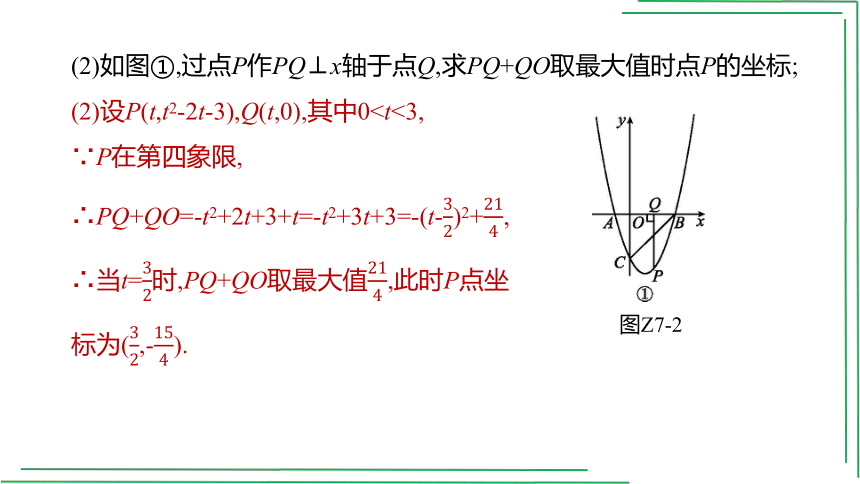
(2)如图①,过点P作PQ⊥x轴于点Q,求PQ+QO取最大值时点P的坐标;
图Z7-2
(2)设P(t,t2-2t-3),Q(t,0),其中0
∴PQ+QO=-t2+2t+3+t=-t2+3t+3=-(t-)2+,
∴当t=时,PQ+QO取最大值,此时P点坐标为(,-).
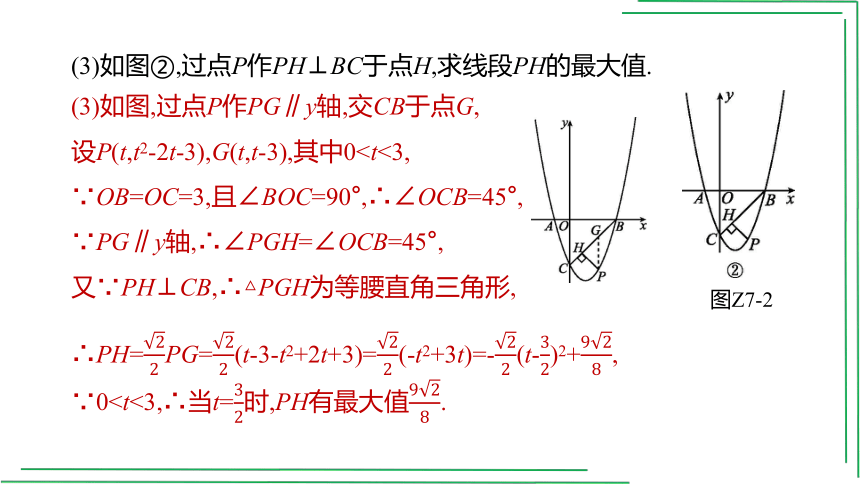
(3)如图②,过点P作PH⊥BC于点H,求线段PH的最大值.
图Z7-2
(3)如图,过点P作PG∥y轴,交CB于点G,
设P(t,t2-2t-3),G(t,t-3),其中0
∵PG∥y轴,∴∠PGH=∠OCB=45°,
又∵PH⊥CB,∴△PGH为等腰直角三角形,
∴PH=PG=(t-3-t2+2t+3)=(-t2+3t)=-(t-)2+,
∵0
【配练】[2020·凉山州]如图Z7-3,二次函数y=ax2+bx+c的图象过
O(0,0),A(1,0),B(,)三点.
(1)求二次函数的解析式;
(2)若线段OB的垂直平分线与y轴交于点C,
与二次函数的图象在x轴上方的部分相交于
点D,求直线CD的解析式;
(3)在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
图Z7-3
(1)求二次函数的解析式;
图Z7-3
解:(1)将点O,A,B的坐标代入二次函数解析式得解得
∴二次函数的解析式为y=x2-x.
(2)若线段OB的垂直平分线与y轴交于点C,与二次函数的图象在x轴上方的部分相交于点D,求直线CD的解析式;
图Z7-3
(2)如图,过B作BH⊥x轴于H,连接AB,
在Rt△OBH中,
tan∠BOH=,
∴∠BOH=30°,
在Rt△AHB中,tan∠BAH=,
∴∠BAH=60°,
又∠BOA+∠OBA=∠BAH,∴∠OBA=∠BAH-∠BOH=60°-30°=30°,
∴△OBA为等腰三角形,
∴OB的垂直平分线CD必过点A(1,0),且平分∠OAB,
∴∠OAC=(180°-∠BAH)=(180°-60°)=60°,
Rt△AOC中,tan∠OAC=,
∴OC=OA·tan∠OAC=1×tan60°=,
∴C点的坐标为(0,).
设直线CD的解析式为y=kx+d,则
解得
∴直线CD的解析式为y=-x+.
(3)在直线CD下方的二次函数的图象上有一动点P,过点P作PQ⊥x轴,交直线CD于Q,当线段PQ的长最大时,求点P的坐标.
图Z7-3
(3)如图,设点P(m,m2-m),
则点Q(m,-m+),-
-m2-m+=-(m+)2+,
∵-<0,故当m=-时,PQ有最大值,此时点P的坐标为(-,).
例2 已知抛物线y=x2-4x+3与x轴交于A,B两点(A在B点左侧),与y轴正半轴交于点C,点P是直线BC上的动点,点Q是线段OC上的动点.
(1)求∠OCB的度数.
(2)如图Z7-4①,求AQ+QP的最小值.
(3)如图②,求OP+PA的最小值,以及
此时点P的坐标.
图Z7-4
(4)如图③,AQ+QC是否存在最小值 若存在,求岀这个最小值;若不存在,请说明理由.
图Z7-4
(1)求∠OCB的度数.
解:(1)令y=0,得x2-4x+3=(x-1)(x-3)=0,
解得x=1或x=3,故A(1,0),B(3,0),
令x=0,得y=3,故C(0,3),∴OC=OB,
又∠BOC=90°,∴∠OCB=45°.
(2)如图Z7-4①,求AQ+QP的最小值.
图Z7-4
(2)如图,设点A关于y轴的对称点为A'(-1,0),则AQ+QP=A'Q+QP≥A'P,
当A',Q,P三点共线,且A'P⊥BC时,AQ+QP最短,
(理由:点线之间,垂线段最短)
Rt△A'PB中,∠OBP=90°-∠OCB=45°,
∴△A'PB是等腰直角三角形,
∴A'P=PB=A'B=2,
∴AQ+QP的最小值为2.
(3)如图②,求OP+PA的最小值,以及此时点P的坐标.
图Z7-4
(3)设点O关于直线BC的对称点为D,连接CD,PD,DB,
根据对称的性质有△OCP≌△DCP,
∴∠DCB=∠OCB=45°,
∠CDB=∠COB=90°,
CO=CD,OP=PD,∴∠OCD=90°,
∴四边形OCDB为正方形,故D(3,3),又A(1,0),
∴OP+PA=DP+PA≥DA=,
当D,P,A三点共线时取等号,(理由:两点之间,线段最短)
此时点P是直线AD:y=x-与直线BC:y=-x+3的交点,
令x-=-x+3,解得x=,
∴OP+PA的最小值为,
此时点P的坐标为(,).
(4)如图③,AQ+QC是否存在最小值 若存在,求岀这个最小值;若不存在,请说明理由.
图Z7-4
(4)如图,在x轴负半轴上找一点G,
使得∠GCO=30°,作QH⊥CG于H,
∴Rt△CQH中,HQ=QC,
∴AQ+QC=AQ+HQ≥AH,
∴当且仅当A,Q,H三点共线,且AH⊥CG时取等号,(理由:点线之间,垂线段最短)
在Rt△COG中,∠GCO=30°,CO=3,
∴GO=CO·tan30°=,
当AH⊥GC时,在Rt△AGH中,
∠HGA=60°,AG=1+,
∴AH=AG·sin60°=,∴AQ+QC的最小值为.
【方法点析】求线段和的最值,一般需要通过对称变换后,通过等量代换,利用“两点之间线段最短”或“点线之间,垂线段最短”求得最值.其变式问题有三角形或四边形的周长最小等.
【配练】[2021·通辽26题节选]如图Z7-5,抛物线y=ax2+bx+3交x轴于A(3,0),B(-1,0)两点,交y轴于点C,动点P在抛物线的对称轴上.
(1)求抛物线的解析式.
(2)当以P,B,C为顶点的三角形周长最小时,
求点P的坐标及△PBC的周长.
图Z7-5
(1)求抛物线的解析式.
图Z7-5
解:(1)将A(3,0),B(-1,0)分别代入y=ax2+bx+3,
得解得:
∴抛物线的解析式为y=-x2+2x+3.
(2)当以P,B,C为顶点的三角形周长最小时,求点P的坐标及△PBC的周长.
图Z7-5
(2)由题意可得,抛物线的对称轴为直线x=-=1.
如图,连接AC交直线x=1于点P, 连接PB,PC,BC.
∵点A与点B关于直线x=1对称,
∴PA=PB,∴PB+PC+BC=PA+PC+BC.
当A,P,C三点共线时,PA+PC的值最小,
即△PBC的周长最小.
设直线AC的解析式为y=kx+h,将A(3,0),C(0,3)分别代入,得
解得
∴直线AC的解析式为y=-x+3,
当x=1时,y=-1+3=2,∴P(1,2).
∵AC==3,BC=,
∴△PBC周长的最小值=PB+PC+BC=AC+BC=+3.
|题型精练|
1.[2021·荆门24题节选]如图Z7-6,抛物线y=ax2+bx+c交x轴于A(-1,0),B(3,0)两点,交y轴于点C(0,-3),点Q为线段BC上的动点.
(1)求抛物线的解析式;
(2)求QO+QA的最小值.
图Z7-6
(1)求抛物线的解析式;
图Z7-6
解:(1)∵抛物线经过A,B两点,
∴设解析式为y=a(x+1)(x-3).
将C(0,-3)代入求得a=1.
∴抛物线的解析式为y=(x+1)(x-3),
即y=x2-2x-3.
(2)求QO+QA的最小值.
图Z7-6
(2)如图,∵OB=OC=3,∠BOC=90°,
∴△OBC是等腰直角三角形.
∴点O(0,0)关于BC的对称点O'
的坐标为(3,-3).
连接AO'交BC于点Q',连接OQ',则当点Q与点Q'重合时,
QO+QA的值最小,
最小值=Q'O+Q'A=Q'O'+Q'A=AO'==5.
2.如图Z7-7,抛物线L:y=x2-x-3与x轴正半轴交于点A,与y轴交于点B.
(1)求直线AB的解析式及抛物线顶点坐标;
(2)点P为第四象限且在对称轴右侧抛物线
上一动点,过点P作PC⊥x轴,垂足为C,PC交
AB于点D,求PD+BD的最大值,并求出此时
点P的坐标.
图Z7-7
(1)求直线AB的解析式及抛物线顶点坐标;
图Z7-7
解:(1)在y=x2-x-3中,令y=0,
则x2-x-3=0.
解得x1=-,x2=4.∴A(4,0).
令x=0,得y=-3,∴B(0,-3).
设直线AB的解析式为y=kx+b,
则解得
∴直线AB的解析式为y=x-3.
∵y=x2-x-3=(x-)2-,
∴抛物线顶点坐标为(,-).
(2)点P为第四象限且在对称轴右侧抛物线
上一动点,过点P作PC⊥x轴,垂足为C,PC交
AB于点D,求PD+BD的最大值,并求出此时
点P的坐标.
图Z7-7
(2)∵OA=4,OB=3,∴AB==5.
设点P的坐标为(x,x2-x-3)(
∵PC⊥x轴,∴PC∥y轴.∴,即.∴BD=x.
∵PD=x-3-(x2-x-3)=-x2+2x.
∴PD+BD=-x2+2x+x=-x2+x=-(x-)2+.
∵-<0,
此时y=()2-=-.∴P(,-).
例3 如图Z7-8,已知抛物线y=-x2-2x+3与x轴负半轴交于点A,与y轴交于点B,顶点为C.
(1)求△ABC的面积;
(2)若点P是抛物线上点A与点B之间的
动点(不包括点A,点B),求△PAB的面积的
最大值,并求出此时点P的坐标;
(3)若点Q是抛物线上的点(不与点C重合),横坐标为m,且S△ABQ=S△ABC,求m的值.
类型二
二次函数与图形面积问题
图Z7-8
(1)求△ABC的面积;
图Z7-8
解:(1)由抛物线的解析式y=-x2-2x+3
可得A(-3,0),B(0,3).
顶点C的坐标为(-1,4),
易求得直线AB的解析式为y=x+3,
如图①,设抛物线对称轴与直线AB交于点D,
则D点坐标为(-1,2),故CD=2,
∴S△ABC=S△ACD+S△BCD=×CD×|xA-xB|=3.
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标;
图Z7-8
(2)如图②,作PM∥y轴,交直线AB于点M,
设P(x,-x2-2x+3),则M(x,x+3),
∴PM=-x2-2x+3-(x+3)=-x2-3x,
∴S△PAB=(-x2-3x)×3=-(x+)2+.
当x=-时,S△PAB最大=,此时yP=-(-)2-2×(-)+3=,
∴△PAB的面积的最大值为,此时点P的坐标为(-,).
(3)若点Q是抛物线上的点(不与点C重合),横坐标为m,且S△ABQ=S△ABC,求m的值.
图Z7-8
(3)[方法一]如图③,过点Q作QN∥y轴,交直线AB于点N,
依题有Q(m,-m2-2m+3),N(m,m+3),
∴QN=|yN-yQ|=|m+3+m2+2m-3|=|m2+3m|,
又S△ABC=3,
∴S△ABQ=×QN×|xA-xB|=
|m2+3m|=3,
当m2+3m>0时,m2+3m=2,
解得m1=,m2=,
当m2+3m<0时,m2+3m=-2,
解得m3=-1(舍去),m4=-2.
综上,符合要求的Q点横坐标m为-2或或.
[方法二]如图④,
①若Q在直线AB上方,过点C作CQ∥AB,
与抛物线的另一个交点为Q,
∵CQ∥AB,即有平行线之间距离处处相等,
且同底AB,
∴S△ABQ=S△ABC,
此时直线CQ的解析式为y=x+5,与y轴交点坐标为(0,5),
令x+5=-x2-2x+3,解得x1=-1(舍去),x2=-2.
②若Q在直线AB的下方,将①中直线CQ向下平移2个单位得到直线AB,再向下平移2个单位得到直线l:y=x+1,直线l与抛物线的交点即为所求,
令x+1=-x2-2x+3,解得x3=,x4=.
综上,符合要求的Q点横坐标m为-2
或或.
【方法点析】如图Z7-9,求由两个定点A,B和动点P组成的△ABP的面积,可过点P作y轴的平行线,交直线AB于点Q,则S△ABP=PQ×|xA-xB|.
图Z7-9
【配练】如图Z7-10,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作
QE∥AC,交BC于点E,连接CQ.当
△CQE的面积最大时,求点Q的坐标.
图Z7-10
(1)求该抛物线的解析式;
图Z7-10
解:(1)由题意,得
解得
∴该抛物线的解析式为:y=-x2+x+4.
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标.
图Z7-10
(2)设点Q的坐标为(m,0),过点E作EG⊥x轴于点G.
由-x2+x+4=0,得x1=-2,x2=4,
∴点B的坐标为(-2,0),∴AB=6,BQ=m+2,
∵QE∥AC,∴△BQE∽△BAC,
∴,即,∴EG=,
∴S△CQE=S△CBQ-S△EBQ=BQ·CO-BQ·EG=(m+2)(4-)=
-m2+m+=-(m-1)2+3,
又∵-2≤m≤4,
∴当m=1时,S△CQE有最大值3,此时Q(1,0).
例4 [2018·日照21题改编]如图Z7-11①,已知点A(-1,0),B(3,0),
C(0,1)在抛物线y=ax2+bx+c上.
(1)求抛物线的解析式及顶点D的坐标;
图Z7-11
(2)如图②,连接CD,AC,BD,求四边形ACDB和△CBD的面积;
(3)如图③,在直线BC上方的抛物线上求一点N,使△NBC面积为1;
图Z7-11
(4)如图④,点E是直线BC上方的抛物线上一点,过点E作x轴的垂线,垂足为F,求△BEF的面积被直线CB平分时点E的坐标.
图Z7-11
(1)求抛物线的解析式及顶点D的坐标;
图Z7-11
解:(1)把A(-1,0),B(3,0),C(0,1)分别代入y=ax2+bx+c,
得解得
所以抛物线的解析式为y=-x2+x+1.
因为y=-x2+x+1=-(x2-2x-3)=-[(x-1)2-4]=-(x-1)2+,
所以D点坐标为(1,).
(2)如图②,连接CD,AC,BD,求四边形ACDB和△CBD的面积;
图Z7-11
(2)OA=1,OB=3,OC=1,DM=,OM=1,BM=2,
S四边形ACDB=S△AOC+S梯形COMD+S△BDM
=×1×1+×(1+)×1+×2×=3.
S△CBD=S四边形ACDB-S△ABC=3-×4×1=1.
(3)如图③,在直线BC上方的抛物线上求一点N,使△NBC面积为1;
图Z7-11
(3)∵B(3,0),C(0,1),
∴直线BC的解析式为y=-x+1,
作NF⊥x轴,交直线BC于H,交x轴于F,
设N(x,-x2+x+1),易得H(x,-x+1).
∴NH=-x2+x+1-(-x+1)=-x2+x.
∴S△NBC=S△NHC+S△NHB=NH(xB-xC)=(-x2+x)·(3-0)=-x2+x.
∵S△NBC=1,∴-x2+x=1,
∴x2-3x+2=0,解得x1=1,x2=2.
∴N1(1,),N2(2,1).
(4)如图④,点E是直线BC上方的抛物线上一点,过点E作x轴的垂线,垂足为F,求△BEF的面积被直线CB平分时点E的坐标.
图Z7-11
(4)设E点坐标为(m,-m2+m+1),直线EF
交BC于点H,当△BEF的面积被直线CB
平分时,EH=HF.所以点H的坐标为
(m,-m2+m+).
因为直线BC的解析式为y=-x+1,
所以点H的坐标为(m,-m+1),所以-m2+m+=-m+1,解得m1=1,m2=3,
m=3不合题意,舍去.
∴当m=1时,△BEF的面积被直线CB平分,此时点E的坐标为(1,),即顶点D.
|题型精练|
1.如图Z7-12,抛物线y=ax2+bx-3与x轴交于点A(-1,0),B,与y轴交于点C,且过点D(2,-3).点P是抛物线上的一个动点.
(1)求抛物线的表达式;
(2)当点P在第四象限运动时,
求四边形ACPB的最大面积.
图Z7-12
(1)求抛物线的表达式;
图Z7-12
解:(1)∵抛物线y=ax2+bx-3经过
点A(-1,0),D(2,-3),
∴解得
∴抛物线的表达式为y=x2-2x-3.
(2)当点P在第四象限运动时,求四边形ACPB的最大面积.
图Z7-12
(2)∵抛物线y=x2-2x-3与y轴交于点C,
∴C(0,-3),CO=3.
令y=0,得x2-2x-3=0,解得x1=-1,x2=3,
∴点B(3,0),OB=3.
连接BC,∵点A(-1,0),∴AB=4,
∴S△ABC=AB·CO=×4×3=6.
∵S四边形ACPB=S△ACB+S△PBC,
∴当△PBC的面积最大时,四边形ACPB的面积最大.
如图,过点P作PQ平行于y轴,交BC于点Q.
由B(3,0),C(0,-3)可知直线BC的表达式为
y=x-3.
设P(m,m2-2m-3)(0
S△PBC=PQ·OB=[-(m-)2+]×3
=-(m-)2+.
∵-<0,∴当m=时,△PBC的面积最大,最大值为.
∵6+,
∴四边形ACPB的面积的最大值为.
2.[2021·荆门24题改编]如图Z7-13,抛物线y=x2-2x-3交x轴于A,B两点,交y轴于C,点Q为线段BC上的动点.过点Q作PQ∥AC交抛物线的第四象限部分于点P,连接PA,PB,记△PAQ与△PBQ的面积分别为S1,S2,设S=S1+S2,求点P坐标,
使得S最大,并求此最大值.
图Z7-13
解:由题意得A(-1,0),B(3,0),C(0,-3),过点P作PE⊥x轴于点E,交BC于点D,连接PC.
∵B(3,0),C(0,-3),∴直线BC的解析式为y=x-3.
设点P的横坐标为m,则PE=-(m2-2m-3),
DE=-(m-3),
PD=PE-DE=-(m2-2m-3)+(m-3)=-m2+3m.
∵PQ∥AC,S1=S△PAQ=S△PCQ.
∴S=S1+S2=S△PCQ+S△PBQ=S△PBC=PD·OB=(-m2+3m)=-(m-)2+,
∴当m=时,S最大,最大值=.
当m=时,y=()2-2×-3=-,
∴点P的坐标为(,-),S的最大值为.
3.[2020·重庆B卷25题节选]如图Z7-14,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)与y轴交于点C,与x轴交于A,B两点(点A在点B的左侧),且A点坐标为(-,0),直线BC的解析式为y=-x+2.
(1)求抛物线的解析式.
(2)过点A作AD∥BC,交抛物线于点D,
点E为直线BC上方抛物线上一动点,
连接CE,BE,BD,DC.求四边形BECD
面积的最大值及相应点E的坐标.
图Z7-14
(1)求抛物线的解析式.
图Z7-14
解:(1)直线BC的解析式为y=-x+2,
当y=0时,x=3,则点B(3,0).
将A(-,0),B(3,0)代入y=ax2+bx+2中,得
解得
∴抛物线的解析式为y=-x2+x+2.
(2)过点A作AD∥BC,交抛物线于点D,点E为直线BC上方抛物线上一动点,连接CE,BE,BD,DC.求四边形BECD
面积的最大值及相应点E的坐标.
图Z7-14
(2)连接AC.∵AD∥CB,
∴S△BCD=S△ABC=×4×2=4.
∴S四边形BECD=S△BCD+S△BCE=4+S△BCE.
过点E作EF∥y轴,交直线BC于点F.
设点E(m,-m2+m+2),则F(m,-m+2),
∴EF=-m2+m+2-(-m+2)=-m2+m.
∴S△BCE=OB·EF=×3×(-m2+m)=-m2+3m=-(m-)2+.
∵-<0,∴当m=时,S△BCE取得最大值,最大值为,此时点E(,),
∴当点E的坐标为(,)时,四边形BECD面积的最大值为+4.
角度1 等腰三角形存在性问题
例5 已知在平面直角坐标系中,点A的坐标为(3,1),请在x轴上找一点P,使△AOP为等腰三角形,则符合条件的点P的坐标为
.
类型三
二次函数与特殊三角形存在性问题
(-,0),(,0),(,0),(6,0)
[解析]方法一(几何法):
①OA=OP时,如图①所示,P1,P3即为所求.
∵OA=,∴OP=,∴点P坐标为(-,0),(,0);
②AO=AP时,如图①所示,P4即为所求,点P坐标为(6,0);
③当PO=PA时,如图①所示,P2即为所求,
如图②,作AB⊥x轴于点B,连接AP2,
设OP2=AP2=x,则BP2=3-x,在Rt△AP2B中,
由勾股定理可知x2=(3-x)2+12,
解得x=,即点P坐标为.
综上所述,点P的坐标为(-,0),,(,0),(6,0).
方法二(代数法):
设点P的坐标为(x,0),易得OA=,OP=|x|,AP= .
①当AO=OP时,=|x|,解得x=±,
此时点P的坐标为(-,0),(,0);
②当AO=AP时,,解得x=0(舍去)或x=6,此时点P的坐标为(6,0);
③当OP=PA时,|x|=,解得x=,此时点P的坐标为.
综上所述,点P的坐标为(-,0),(,0),(,0),(6,0).
【方法点析】求解等腰三角形的存在性问题有两种基本方法:
(1)代数法:适用于三角形的边长容易由勾股定理求解的情况.步骤如下:
①根据点的坐标,表示出AB2,BC2,CA2;
②根据等腰三角形的性质,可得到三个方程:
AB2=BC2,BC2=CA2,CA2=AB2;
③分别解这三个方程,若能得到方程有解,则这个解即为所求;若方程无解,则不存在这样的三角形.
(2)几何法(两圆一线):
①满足条件的点C在如图Z7-15所示的分别以点A,B为圆心,以线段AB长为半径的圆上或在线段AB的垂直平分线上(除去与AB在一条直线上的点).
②利用勾股定理、相似、三角函数等求线段长,得出点的坐标.
图Z7-15
例6 如图Z7-16,已知抛物线y=-x2-4x+12与x轴交于点A,B(A在B的左侧),与y轴交于点C.
(1)x轴上是否存在点F,使得△BCF是以BC
为底边的等腰三角形 若存在,求出点F的
坐标;若不存在,说明理由.
图Z7-16
(2)x轴上是否存在点M,使得△BCM是以BC为腰的等腰三角形 若存在,求出点M的坐标;若不存在,说明理由.
(3)在抛物线的对称轴上是否存在点G,使得△BCG为等腰三角形 若存在,求出点G的坐标;若不存在,说明理由.
图Z7-16
(4)设抛物线的顶点为D,点P在抛物线上,点H在抛物线的对称轴上,是否存在点P使得△PDH是等边三角形 若存在,求出P点的坐标;若不存在,说明理由.
图Z7-16
(1)x轴上是否存在点F,使得△BCF是以BC为底边的等腰三角形 若存在,求出点F的坐标;若不存在,说明理由.
图Z7-16
解:(1)令x=0,则y=12,
令y=0,则-x2-4x+12=0,解得x1=-6,x2=2.
∴A(-6,0),B(2,0),C(0,12).
设点F的坐标为(t,0).
由已知得OC=12,FB=2-t,FC=
,
∵△BCF是以BC为底边的等腰三角形,
∴FB=FC,即2-t=,解得t=-35.
∴点F的坐标为(-35,0).
(2)x轴上是否存在点M,使得△BCM是以BC为腰的等腰三角形 若存在,求出点M的坐标;若不存在,说明理由.
图Z7-16
(2)∵B(2,0),C(0,12),
∴利用勾股定理可得BC==2.
因为△BCM是以BC为腰的等腰三角形,所以分两种情况:
①BM=BC时,M1(2-2,0),M2(2+2,0);
②CM=CB时,M3(-2,0).
综上所述,当M的坐标为(2-2,0)或(2+2,0)或
(-2,0)时,△BCM是以BC为腰的等腰三角形.
(3)在抛物线的对称轴上是否存在点G,使得△BCG为等腰三角形 若存在,求出点G的坐标;若不存在,说明理由.
图Z7-16
(3)由(2)得BC=2.设点G(-2,n),
△BCG为等腰三角形分三种情况:
①当CG=CB时,CG=.
∵CG=CB,∴=2,
解得n1=0,n2=24(不合题意,舍去),
故G的坐标为(-2,0).
②当BC=BG时,BG=,
∵BC=BG,∴=2,
解得n3=2,n4=-2.
因此点G的坐标为(-2,2)或(-2,-2).
③当BG=CG时,GC=,GB=,
∵GC=GB,∴,解得n=5.5,故点G坐标为
(-2,5.5).
综上所述,当G的坐标为(-2,0)或(-2,2)或(-2,-2)或(-2,5.5)时,
△BCG为等腰三角形.
(4)设抛物线的顶点为D,点P在抛物线上,点H在抛物线的对称轴上,是否存在点P使得△PDH是等边三角形 若存在,求出P点的坐标;若不存在,说明理由.
图Z7-16
(4)设点P(m,-m2-4m+12),过点P作PN
垂直于抛物线的对称轴,垂足为N,
∵y=-x2-4x+12=-(x+2)2+16,
∴D(-2,16).
由于△PDH是等边三角形,由等边三角形的性质得PN=ND,而PN=|m-(-2)|=|m+2|,ND=16-(-m2-4m+12)=(m+2)2,
由PN=ND,得|m+2|=(m+2)2,
解得m1=-2,m2=--2,m3=-2(不合题意,舍去).
因此P点的坐标是(-2,)或(--2,).
角度2 直角三角形存在性问题
例7 如图Z7-17,已知直线y=kx-6经过点A(1,-4),与x轴相交于点B,若点Q是y轴上一点,且△ABQ为直角三角形,则点Q的坐标
为 .
图Z7-17
(0,-)或(0,)或(0,-1)或(0,-3)
[解析]方法一:将(1,-4)代入y=kx-6中,解得k=2,
∴直线解析式为y=2x-6,∴B(3,0).
设直线AB交y轴于点C,则C(0,-6),由题意知AB2=20,
设Q(0,y).
①当∠QAB=90°时,AQ2+AB2=BQ2.
∵AQ2=CQ2-AC2=(y+6)2-5=y2+12y+31,BQ2=OQ2+OB2=y2+9,
∴y2+12y+31+20=y2+9,
解得y=-,∴Q(0,-).
②当∠QBA=90°时,AB2+BQ2=AQ2.
∵AQ2=y2+8y+17,BQ2=y2+9,∴20+y2+9=y2+8y+17,
解得y=,∴Q(0,).
③当∠AQB=90°时,AQ2+BQ2=AB2.
∵AQ2=y2+8y+17,BQ2=y2+9,∴y2+8y+17+y2+9=20,
解得y=-1或y=-3,
∴Q(0,-1)或Q(0,-3).
综上,Q点的坐标为(0,-),(0,),(0,-1)或(0,-3).
方法二:设直线AB与y轴交于点D,
易得D(0,-6),B(3,0),AD=,BD=3.
①如图①,当∠Q1AB=90°时,
∵∠Q1AD=∠DOB=90°,∠Q1DA=∠ODB,
∴△DAQ1∽△DOB,
∴,即,∴DQ1=,
∴OQ1=,即Q1(0,-);
②如图②,当∠Q2BA=90°时,
∵∠Q2OB=∠BOD,∠Q2BO=∠ODB,
∴△BOQ2∽△DOB,
∴,即,
∴OQ2=,即Q2(0,);
③如图③,以AB为直径画圆与y轴分别交于点Q3,Q4,作AE⊥y轴,垂足为点E,
易得△AEQ3∽△Q3OB,
∴,即,
解得OQ3=1或OQ3=3,
∴Q3(0,-3),Q4(0,-1).
综上,Q1(0,-),Q2(0,),Q3(0,-3),Q4(0,-1).
【方法点析】求解直角三角形的存在性问题的常用方法有两种:
(1)代数法:设出一个点的坐标,表示出AB2,BC2,CA2,
分三种情况:①AB2=BC2+CA2;②BC2=CA2+AB2;
③CA2=AB2+BC2,根据不同的情况建立方程求解.
(2)几何法:
①两线一圆作出点:如图Z7-18,满足条件的点C在如图所示的分别过点A,B且垂直AB的直线上或在以线段AB为直径的圆上(除去与AB在一条直线上的点).
②构造相似(常需要构造一线三等角相似),利用对应边成比例求线段长,进而求得点的坐标.
图Z7-18
例8 如图Z7-19,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(-1,0)两点,与y轴交于点C.
(1)求这条抛物线对应的函数表达式.
(2)问在y轴上是否存在点P,使得△PAM为直角三角形 若存在,求出点P的坐标;若不存在,说明理由.
(3)设点H是第一象限内抛物线上的动点,
点Q是线段AC上的一点,是否存在点H,Q
使得△HCQ是等腰直角三角形 若存在,
求出点Q的坐标;若不存在,请说明理由.
图Z7-19
(1)求这条抛物线对应的函数表达式.
图Z7-19
解:(1)将A,B两点坐标代入抛物线表达式,
得解得
∴y=-x2+2x+3.
(2)问在y轴上是否存在点P,使得△PAM为直角三角形 若存在,求出点P的坐标;若不存在,说明理由.
图Z7-19
(2)方法一:存在点P,使△PAM是直角三角形.
∵y=-x2+2x+3=-(x-1)2+4,∴M(1,4).
如图①,当点M为直角顶点时,
过M作EF⊥y轴于点E,过A作
AF⊥EF于点F.
∵∠AMP=90°,
∴∠EMP+∠AMF=90°,易知∠F=90°,
∴∠AMF+∠MAF=90°,∴∠EMP=∠MAF.
又∵∠AFM=∠PEM,∴△EPM∽△FMA,
∴,∴,∴PE=,∴P(0,).
如图②,当点A为直角顶点时,过A作EF⊥x轴,
过M作MF⊥AF于F,过P作PE⊥AE于点E,
同上可证△EPA∽△FAM,∴,
∴,∴AE=,∴P(0,-).
如图③,当点P为直角顶点时,过M作ME⊥y轴于E,
∴△EPM∽△OAP,∴,∴,解得PE=1或3,
∴P(0,3)或(0,1).
综上所述,使△PAM是直角三角形的
点P的坐标是(0,),(0,-),(0,3),(0,1).
方法二:存在点P使得△PAM是直角三角形.
易得M(1,4),A(3,0),设P(0,m).
∴AP2=(3-0)2+(0-m)2=m2+9,AM2=(3-1)2+(0-4)2=20,
MP2=(1-0)2+(4-m)2=m2-8m+17.
当∠APM=90°时,AP2+MP2=AM2,
即m2+9+m2-8m+17=20,
∴m1=1,m2=3.∴P1(0,1),P2(0,3).
当∠PAM=90°时,AP2+AM2=MP2,
即m2+9+20=m2-8m+17,∴m=-,∴P3(0,-).
当∠PMA=90°时,MP2+AM2=AP2,
即m2-8m+17+20=m2+9,∴m=,∴P4(0,).
综上,点P的坐标为(0,1)或(0,3)或(0,-)或(0,).
(3)设点H是第一象限内抛物线上的动点,
点Q是线段AC上的一点,是否存在点H,Q
使得△HCQ是等腰直角三角形 若存在,
求出点Q的坐标;若不存在,请说明理由.
图Z7-19
(3)存在点H,Q,使△HCQ是等腰直角三角形.
①如图,当∠HCQ=90°时,要使Rt△HCQ为
等腰直角三角形,则有∠CQH=45°,HC=QC.
∵△OAC为等腰直角三角形,
∴∠OCA=∠OAC=45°.∴QH∥y轴.
设H(n,-n2+2n+3),则Q(n,-n+3),
则HC2=n4-4n3+5n2,QC2=2n2,
∴n4-4n3+5n2=2n2,
解得n=0(舍去)或1或3(舍去),∴H(1,4),Q(1,2).
②当∠CHQ=90°时,CH∥x轴,HQ∥y轴,此时∠QCH=∠CQH=45°,△CHQ为等腰直角三角形.
由图象易得点C与点H关于对称轴对称,∴H(2,3),Q(2,1).
③当∠CQH=90°时,∠QCH=∠CHQ=45°,
∴CH∥x轴,
如图,过点Q作QT⊥CH,垂足为T.
∵△CHQ是等腰直角三角形,QT⊥CH,
∴CT=HT,∴Q在对称轴上,
∴Q(1,2).
综上,点Q的坐标为(1,2)或(2,1).
|题型精练|
1.[2020·无锡]二次函数y=ax2-3ax+3的图象过点A(6,0),且与y轴交于点B,点M在该抛物线的对称轴上,若△ABM是以AB为直角
边的直角三角形,则点M的坐标为 .
(,-9)或(,6)
[解析]把点A(6,0)代入y=ax2-3ax+3,得0=36a-18a+3,
解得:a=-,∴y=-x2+x+3,
∴B(0,3),抛物线的对称轴为直线x=-.
设点M的坐标为(,m),
当∠ABM=90°时,过B作BD⊥对称轴于D,如图,
则∠1=∠2,∴tan∠2=tan∠1==2,
∴=2,∴DM=3,∴M(,6).
当∠M'AB=90°时,∠1=∠3,
∴tan∠3==tan∠1==2,∴M'N=9,∴M'(,-9).
综上所述,点M的坐标为(,-9)或(,6).
2.[2021·湖州]已知在平面直角坐标系xOy中,点A的坐标为(3,4),M是抛物线y=ax2+bx+2(a≠0)对称轴上的一个动点.小明经探究发现:当的值确定时,抛物线的对称轴上能使△AOM为直角三角形的点M的个数也随之确定,若抛物线y=ax2+bx+2
(a≠0)的对称轴上存在3个不同的点M,使△AOM为直角三角形,则的值是 .
2或-8
[解析] ∵△AOM是直角三角形,
∴一定存在两个以A,O为直角顶点的直角
三角形,且点M在对称轴上的直角三角形,
∴当以OA为直径的圆与抛物线的对称轴
x=-相切时,对称轴上存在1个以M为直角顶点的直角三角形,此时对称轴上存在3个不同的点M,使△AOM为直角三角形(如图所示).
易知,-=-1或4,∴=2或-8,故答案为:2或-8.
3.[2020·徐州28题节选]如图Z7-20,在平面直角坐标系中,函数y=-ax2+
2ax+3a(a>0)的图象交x轴于点A,B,交y轴于点C,它的对称轴交x轴于点E.过点C作CD∥x轴交抛物线于点D,连接DE并延长交y轴于点F,交抛物线于点G.直线AF交CD于点H,交抛物线于点K,连接HE,GK.
(1)点E的坐标为: ;
(2)当△HEF是直角三角形时,求a的值.
图Z7-20
(1,0)
[解析]对于抛物线y=-ax2+2ax+3a,它的对称轴为直线x=-=1,
∴E点的坐标为(1,0).
(2)当△HEF是直角三角形时,求a的值.
图Z7-20
(2)对于抛物线y=-ax2+2ax+3a,
令y=0,有-ax2+2ax+3a=0,解得x1=-1,x2=3,
∴A点的坐标为(-1,0),B点的坐标为(3,0),
令x=0,则y=3a,∴点C的坐标为(0,3a),
由于CD∥x轴,∴点D和点C关于抛物线的对称轴对称,
∴点D的坐标为(2,3a),
设直线DE的解析式为y=kx+b,代入(1,0)和(2,3a),
有解得∴直线ED的解析式为y=3ax-3a,
令x=0,则y=-3a,
∴点F的坐标为(0,-3a),
解方程组得G的坐标为(-3,-12a),
同理可求得直线HK的解析式为:y=-3ax-3a,点K的坐标为(6,-21a),
对于直线y=-3ax-3a,令y=3a,解得H的坐标为(-2,3a),
∴H(-2,3a),E(1,0),F(0,-3a),
∴HE2=9a2+9,HF2=36a2+4,EF2=9a2+1,
当HE2=HF2+EF2时,有9a2+9=36a2+4+9a2+1,
解得a=(舍负),
当HF2=HE2+EF2时,有36a2+4=9a2+9+9a2+1,
解得a=(舍负),
当EF2=HE2+HF2时,有9a2+1=9a2+9+36a2+4,无解,
∴a的值为或.
4.[2021·宿迁28题节选]如图Z7-21,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(4,0),与y轴交于点C.连接AC,BC,点P在抛物线上运动.若点P在第一象限,直线AP交BC于
点F,过点P作x轴的垂线交BC于点H,
当△PFH为等腰三角形时,求线段PH
的长.
图Z7-21
解:将A(-1,0),B(4,0)代入y=-x2+bx+c中,可解得b=,c=2,
∴y=-x2+x+2,令x=0,得y=2,∴C(0,2),
由B(4,0),C(0,2)得直线BC的解析式为y=-x+2.
设PH与x轴的交点为N,P(a,-a2+a+2),则H(a,-a+2),PH=-a2+2a,
若FP=FH,则∠FPH=∠FHP=∠BHN=∠BCO,
∴tan∠APN=tan∠BCO=2,∴AN=2PN,
即a+1=2(-a2+a+2),
解得a=3或a=-1(舍去),此时PH=.
若PF=PH,过点F作FM⊥y轴于点M.
由题意知AB=5,AC=,BC==2,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,且∠ACB=90°,
易知∠PFH=∠PHF,
∵∠CFA=∠PFH,∠NHB=∠PHF,
∴∠CFA=∠NHB,
又∵∠ACF=∠BNH=90°,
∴△ACF∽△BNH,∴∠CAF=∠NBH,
∴,∴CF=AC=.
∵FM⊥y轴,∴FM∥OB,
∴∠CPM=∠CBO,∴,
在Rt△CMF中,由CF=,得MF=1,CM=,∴F(1,),
∴直线AF的解析式为y=x+,
联立抛物线解析式得x+=-x2+x+2,
解得x=或x=-1(舍去),此时PH=.
若HF=HP,过点C作CE∥AB交AP于点E,
∵∠CAF+∠CFA=90°,∠PAN+∠HPF=90°,
∠CFA=∠HFP=∠HPF,
∴∠CAF=∠PAN,即AP平分∠CAB,
∴CE=CA=,∴E(,2),
∴直线AE的解析式为:y=x+,
联立抛物线解析式得x+=-x2+x+2,
解得x=5-或x=-1(舍去).
此时PH=3-5.
综上,线段PH的长为或3-5或.
5.[2021·随州24题节选]在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于点A和点B,与y轴交于点C,如图Z7-22,M是直线BC上一个动点,过点M作MN⊥x轴交抛物线于点N,Q是直线AC上一个动点,当△QMN为等腰直角三角形
时,求此时点M及其对应点Q的坐标.
图Z7-22
解:抛物线y=x2-2x-3与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C(0,-3),设直线AC解析式为y=m1x+n1,直线BC解析式为y=m2x+n2,
∵A(-1,0),C(0,-3),∴
解得∴直线AC解析式为y=-3x-3.
∵B(3,0),C(0,-3),∴解得
∴直线BC解析式为y=x-3.
设M(t,t-3),则N(t,t2-2t-3),
∴MN=|t2-2t-3-(t-3)|=|t2-3t|,
①当△QMN是以NQ为斜边的等腰直角三角形时,此时∠NMQ=90°,MN=MQ,如图①,
②当△QMN是以MQ为斜边的等腰直角三角形时,此时∠MNQ=90°,MN=NQ,如图②,
③当△QMN是以MN为斜边的等腰直角三角形时,此时∠MQN=90°,MQ=NQ,如图③,
综上所述,点M及其对应点Q的坐标为:M1(,),Q1(-,);M2(,-) ,
Q2(-,-);M3(5,2),Q3(-5,12);M4(2,-1),Q4(0,-3);M5(7,4),Q5(-7,18);
M6(1,-2),Q6(0,-3).
例9 如图Z7-23,在平面直角坐标系中,已知点A(-3,4),B(-6,-2),
C(6,-2),若以点A,B,C,D为顶点作平行四边形,则点D的坐标为
.
类型四
二次函数与特殊四边形存在性问题
图Z7-23
(-15,4)或(3,-8)或(9,4)
【方法点析】已知三定点,探求第四个点,使之构成平行四边形,构图方法:作平行线.
如图Z7-24,根据平行四边形的性质,分别过三个定点A,B,C作各自对边的平行线,三条平行线的交点即为点D的位置.
图Z7-24
例10 如图Z7-25,已知抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点P是抛物线在第一象限内的一个动点,且点P的横坐标为t.
(1)求抛物线的表达式.
(2)设抛物线的对称轴为l,与x轴的交点为D.
在直线l上是否存在点M,使得四边形CDPM
是平行四边形 若存在,求出点M的坐标;若
不存在,请说明理由.
图Z7-25
(3)变式1:如图Z7-26,点N在x轴上,点Q在抛物线上,若以点C,D,N,Q为顶点的四边形是平行四边形,求出所有点N的坐标.
(4)变式2:如图Z7-27,点E是线段OB上的动点,过点E作x轴的垂线l',交抛物线于点F,在抛物线上是否存在点T,使四边形CETF是矩形 若存在,求出E点坐标;若不存在,请说明理由.
图Z7-26
图Z7-27
(1)求抛物线的表达式.
图Z7-25
解:(1)∵抛物线y=-x2+bx+c经过
A(-1,0),B(3,0)两点,
∴抛物线的表达式为y=-(x+1)(x-3),
即y=-x2+2x+3.
(2)设抛物线的对称轴为l,与x轴的交点为D.在直线l上是否存在点M,使得四边形CDPM是平行四边形 若存在,求出点M的坐标;若不存在,请说明理由.
图Z7-25
(2)如图,连接PC,设PC交抛物线对称轴l:直线x=1于点H,
当CP与DM互相平分时,四边形CDPM是平行四边形,
此时H为CP的中点,H为DM的中点,
∴=xH,而xC=0,xH=1,
∴xP=2,故点P(2,3),又C(0,3),
∴H(1,3),MH=HD=3,
∴M(1,6).
(3)变式1:如图Z7-26,点N在x轴上,点Q在抛物线上,若以点C,D,
N,Q为顶点的四边形是平行四边形,求出所有点N的坐标.
图Z7-26
(3)变式1:依题设N(n,0),Q(m,-m2+2m+3),
①CD为对角线时,CD与QN互相平分,
则
解得(舍去)
或此时Q(2,3),N(-1,0).
②CQ为对角线时,CQ与DN互相平分,
则
解得或
此时Q(1+,-3),N(,0)或Q(1-,-3),N(-,0).
③DQ为对角线时,DQ与CN互相平分,
则
解得(舍去)或
此时Q(2,3),N(3,0).
综上,符合要求的点N的坐标为
(-1,0),(,0),(-,0),(3,0).
(4)变式2:如图Z7-27,点E是线段OB上的动点,过点E作x轴的垂线l',交抛物线于点F,在抛物线上是否存在点T,使四边形CETF是矩形 若存在,求出E点坐标;若不存在,请说明理由.
图Z7-27
变式2:不存在点T,使四边形CETF是矩形.理由:假设存在点F,则当∠ECF=90°,且CT与EF互相平分时,四边形CETF为矩形,
设E(a,0),则F(a,-a2+2a+3),其中0
解得
故T(2a,-a2+2a),
将T点坐标代入抛物线解析式得-4a2+4a+3=-a2+2a,
化简,得3a2-2a-3=0,
解得a1=,a2=(舍去).
另一方面,若∠ECF=90°,则有CF2+CE2=EF2,
即a2+(-a2+2a)2+a2+32=(-a2+2a+3)2=(-a2+2a)2+6(-a2+2a)+32,
解得a3=0(舍去),a4=,
由a1≠a4说明不存在a的值同时满足条件:∠ECF=90°,CT与EF互相平分,∴抛物线上不存在点T,使四边形CETF是矩形.
【方法点析】(1)对于两个定点,两个动点的问题,一般思路是先用一个未知数表示相对简单的那个动点的坐标,将这三个点看成定点,用该未知数表示另一个动点的坐标,再根据条件求相应点的坐标.
(2)矩形存在问题可以转化为直角三角形存在问题;菱形存在问题可以转化为等腰三角形存在问题;正方形存在问题可以转化为等腰直角三角形存在问题.
|题型精练|
1.如图Z7-28,抛物线y=-x2+2x+3交x轴于A,B两点,交y轴于点C,动点P在抛物线的对称轴上.若点Q是平面直角坐标系内的任意一点,是否存在点Q,使得以A,C,P,Q
为顶点的四边形是菱形 若存在,求出
所有符合条件的点Q的坐标;若不存在,
请说明理由.
图Z7-28
解:令y=0,则-x2+2x+3=0,解得x1=-1,x2=3,
∴A(3,0),B(-1,0).
令x=0,则y=3,∴C(0,3).
设P(1,t),①以AC为边时,如图①,
∵四边形ACPQ是菱形,∴CP=CA,
∴12+(3-t)2=32+32,解得:t=3±,
∴P1(1,3-),P2(1,3+),
∴Q1(4,-),Q2(4,).
如图②,∵四边形ACQP是菱形,∴AC=AP,
∴(3-1)2+t2=32+32,解得t=±.
∴P3(1,),P4(1,-),
∴Q3(-2,3+),Q4(-2,3-).
②以AC为对角线时,如图③,
∵四边形APCQ是菱形,∴CP=PA,
∴12+(3-t)2=(1-3)2+t2,
解得:t=1,∴P5(1,1),Q5(2,2),
综上所述,符合条件的点Q的坐标为:(4,-)或(4,)或
(-2,3+)或(-2,3-)或(2,2).
2.如图Z7-29,在平面直角坐标系中,抛物线y=-x2+2x+与x轴交于点A,B,与y轴交于点C,连接BC,点D为此抛物线的顶点.点P在抛物线对称轴上,平面内存在点Q,使以点B,C,P,Q为顶点的四边形为矩形,求点Q的坐标.
图Z7-29
解:令y=0,则-x2+2x+=0,解得x=-1或x=5.
∴A(-1,0),B(5,0),
令x=0,则y=,∴C(0,),易知对称轴为直线x=2.
设P(2,y),Q(m,n),
①若BC为矩形的对角线,
则解得:
又∵∠BPC=90°,∴PC2+PB2=BC2,
即:22+(-y)2+32+y2=52+()2,
解得y=4或y=-,∴n=-或n=4,
∴Q(3,-)或Q(3,4).
②若BP为矩形的对角线,则解得
又∵∠BCP=90°,∴BC2+CP2=BP2,
即:52+()2+22+(-y)2=32+y2,解得y=,∴Q(7,4).
③若BQ为矩形的对角线,则解得:
又∵∠BCQ=90°,∴BC2+CQ2=BQ2,
即:52+()2+m2+(-n)2=(5-m)2+n2,
解得n=-,∴Q(-3,-),
综上所述,点Q的坐标为(3,-)或(3,4)或(7,4)或(-3,-).
例11 [2020·怀化24题改编]如图Z7-30所示,抛物线y=x2-2x-3与x轴相交于A,B两点,与y轴相交于点C,点M为抛物线的顶点.
(1)求点C及顶点M的坐标.
(2)连接AC,BM,CM,BC,判断△BCM和
△AOC是否相似 请说明理由.
(3)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P,E,O为顶点的三角形与△ABC相似 若存在,求出点P的坐标;若不存在,请说明理由.
类型五
二次函数与相似三角形存在性问题
图Z7-30
(1)求点C及顶点M的坐标.
图Z7-30
解:(1)将x=0代入y=x2-2x-3,得y=-3,故点C的坐标为(0,-3),
又∵y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点M的坐标为(1,-4).
(2)连接AC,BM,CM,BC,判断△BCM和△AOC是否相似 请说明理由.
图Z7-30
(2)相似.理由如下:
令y=x2-2x-3=0,解得:x=3或x=-1,
∴B(3,0),A(-1,0),
∴BC==3,CM=,BM=2,
又AC=,∴,
∴△AOC∽△MCB.
(3)直线CM交x轴于点E,若点P是线段EM上的一个动点,是否存在以点P,E,O为顶点的三角形与△ABC相似 若存在,求出点P的坐标;若不存在,请说明理由.
图Z7-30
(3)点P的坐标为(-,-)或(-1,2),
连接OP,如图所示.
∵C(0,-3),M(1,-4),
∴直线MC的解析式为:y=-x-3,
将y=0代入直线MC的解析式得E点坐标为(-3,0),
∴OE=OB=3,且OC⊥BE,∴CE=CB,∴∠CBE=∠CEB,
设P(x,-x-3),
又∵P点在线段EM上,∴-3
由题意知:△PEO与△ABC相似,分两种情况讨论:
①当△PEO∽△CBA时,
有,∴,
解得x=-,满足-3
解得x=-1,满足-3
【方法点析】相似三角形存在问题,往往需要先确定一组对应角相等,然后利用这组角的夹边对应成比例即可列式求解,夹边的对应需要分成两类讨论.或者利用等角的三角函数列方程.如果等角不能确定,那么就需要对角进行讨论,注意三角形中的特殊角,包括已知三角函数值的角.
|题型精练|
1.[2021·陕西]已知抛物线y=-x2+2x+8与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求点B,C的坐标.
(2)设点C'与点C关于该抛物线的对称轴对称.在y轴上是否存在点P,使△PCC'与△POB相似,且PC与PO是对应边 若存在,求出点P的坐标;若不存在,请说明理由.
(1)求点B,C的坐标.
解:(1)∵y=-x2+2x+8,令x=0,得y=8,
∴C(0,8),
令y=0,得-x2+2x+8=0,
解得:x1=-2,x2=4,∴B(4,0).
(2)设点C'与点C关于该抛物线的对称轴对称.在y轴上是否存在点P,使△PCC'与△POB相似,且PC与PO是对应边 若存在,求出点P的坐标;若不存在,请说明理由.
(2)存在,由已知得,该抛物线的对称轴为直线x=1,
∵点C'与点C关于直线x=1对称,
∴C'(2,8),CC'=2.∴CC'∥OB.
∵点P在y轴上,∴∠PCC'=∠POB=90°,
∴当时,△PCC'∽△POB.设P(0,y),
当y>8时,则,∴y=16.∴P(0,16).
当0
∴点P不存在.
∴P(0,16)或P(0,).
2.[2021·无锡27题节选]在平面直角坐标系中,O为坐标原点,直线y=-x+3与x轴交于点B,与y轴交于点C(如图Z7-31),二次函数y=ax2+2x+c的图象过B,C两点,且与x轴交于另一点A,点M为线段OB上的一个动点,过点M作直线l平行于y轴交BC于点F,交二次函数y=ax2+2x+c的图象于点E.
(1)求二次函数的表达式;
(2)当以C,E,F为顶点的三角形与
△ABC相似时,求线段EF的长度.
图Z7-31
(1)求二次函数的表达式;
图Z7-31
解:(1)∵直线y=-x+3,∴B(3,0),C(0,3),
把B,C坐标代入抛物线y=ax2+2x+c,
得解得
∴二次函数的表达式为y=-x2+2x+3.
(2)当以C,E,F为顶点的三角形与△ABC相似时,求线段EF的长度.
图Z7-31
(2)根据题意画图如图,
令y=0,则-x2+2x+3=0,解得x1=-1,x2=3,
∴A(-1,0),∴AB=4,BC=3.
∵OB=OC,∴∠OBC=45°,
∵FM⊥OB,∴∠CFE=∠MFB=45°,
∴∠CFE=∠ABC.
设E(m,-m2+2m+3),则F(m,-m+3),
∴EF=-m2+3m,CF=m.
①当时,△ABC∽△CFE,
∴,
解得m1=0(舍去),m2=,
∴EF=-m2+3m=;
②当时,△ABC∽△EFC,
∴,
解得m1=0(舍去),m2=,∴EF=-m2+3m=;
综上所述,EF=或.
例12 [2020·张家界23题改编]如图Z7-32,抛物线y=ax2-6x+c交x轴于A,B两点,交y轴于点C,直线y=-x+5经过点B,C.
(1)求抛物线的解析式及∠ACB的正切值.
(2)点P是抛物线上的动点,当∠PAB=∠ACB时,求点P的坐标.
(3)在直线BC上是否存在点M,使AM与直线BC的
夹角等于∠ACB的2倍 若存在,请求出点M的坐标;
若不存在,请说明理由.
类型六
二次函数与角度的结合问题
图Z7-32
(1)求抛物线的解析式及∠ACB的正切值.
图Z7-32
解:(1)∵直线y=-x+5经过点B,C,
∴C(0,5),B(5,0),将B,C坐标分别代入y=ax2-6x+c,
得解得
∴该抛物线的解析式为y=x2-6x+5,
如图①,过点A作直线BC的垂线,
垂足为H,
令x2-6x+5=0,解得x=1或x=5,故A(1,0),又∵C(0,5),B(5,0),
∴BC==5,AB=4,OC=5,AC=,
∴S△ABC=×AB×OC=×BC×AH,即4×5=5×AH,解得AH=2,
在Rt△AHC中,由勾股定理得:
CH==3,
∴tan∠ACB=.
(2)点P是抛物线上的动点,当∠PAB=∠ACB时,求点P的坐标.
图Z7-32
(2)如图①,作PG⊥x轴于点G,设G(m,0),
P(m,m2-6m+5),
在Rt△APG中,tan∠PAB=,
又∵∠PAB=∠ACB,
∴=|m-5|,解得m=或m=,∴P点坐标为(,)或(,-).
(3)在直线BC上是否存在点M,使AM与直线BC的夹角等于∠ACB的2倍 若存在,请求出点M的坐标;若不存在,请说明理由.
图Z7-32
(3)存在.理由如下:如图②,作线段AC的
垂直平分线交直线BC于点M1,
∴M1C=M1A,
∴∠ACM1=∠CAM1=∠AM1B,
即∠AM1B=2∠ACB,
∵直线BC的解析式为y=-x+5,
∴设M1(t,-t+5),又∵A(1,0),
∴由A=C得(t-1)2+(-t+5)2=t2+(-t+5-5)2,
解得t=,
∴M1坐标为(,).
作点M1关于点H的对称点M2,有AM1=AM2,故∠AM2C=∠AM1B=2∠ACB,
设M2(s,-s+5),又∵A(1,0),
∴由A=A得(-1)2+()2=(s-1)2+(-s+5)2,解得s=或s=,∴M2坐标为(,).
综上,M点坐标为(,)或(,).
【方法点析】等角条件时,可以先求出已知角的正切值,然后根据函数解析式设元,构造直角三角形,利用正切值列方程.倍角条件时,需要借助辅助线转换为等角条件,常用的辅助线有构造平行线,或者构造等腰三角形,构造辅助圆等.
|题型精练|
[2019·咸宁24题节选]如图Z7-33,在平面直角坐标系中,直线y=
-x+2与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过A,B两点且与x轴的负半轴交于点C.
(1)求该抛物线的解析式;
(2)若点D为直线AB上方抛物线上的一个动点,
当∠ABD=2∠BAC时,求点D的坐标.
图Z7-33
(1)求该抛物线的解析式;
图Z7-33
解:(1)在y=-x+2中,令y=0,得x=4,令x=0,得y=2,
∴A(4,0),B(0,2),代入y=-x2+bx+c
得解得
∴抛物线的解析式为y=-x2+x+2.
(2)若点D为直线AB上方抛物线上的一个动点,当∠ABD=
2∠BAC时,求点D的坐标.
图Z7-33
(2)如图,过点B作x轴的平行线交抛物线于点E,过点D作BE的垂线,垂足为F,
∵BE∥x轴,∴∠BAC=∠ABE,
∵∠ABD=2∠BAC,∴∠ABD=2∠ABE,
即∠DBE+∠ABE=2∠ABE,
∴∠DBE=∠ABE,∴∠DBE=∠BAC,
设D点的坐标为,则BF=x,DF=-x2+x,
∵tan∠DBE=,tan∠BAC=,
∴,即,
解得x1=0(舍去),x2=2,
当x=2时,-x2+x+2=3,
∴点D的坐标为(2,3).
例13 已知抛物线y=ax2+bx+c(a≠0)的顶点坐标是(2,1),并且经过点(4,2).直线y=x+1与抛物线交于B,D两点.
(1)求抛物线的解析式.
(2)以BD为直径作圆,圆心为点C,
求证:圆C与x轴相切.
类型七
二次函数与圆的结合问题
图Z7-34
(3)圆C与直线m交于抛物线的对称轴右侧的点M(t,1).直线m上每一点的纵坐标都等于1.过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F.求BE∶MF的值.
图Z7-34
(1)求抛物线的解析式.
图Z7-34
解:(1)设抛物线的解析式为y=a(x-h)2+k,
∵抛物线的顶点坐标是(2,1),
∴y=a(x-2)2+1,
又∵抛物线经过点(4,2),
∴2=a(4-2)2+1,
解得a=,
∴抛物线的解析式是y=(x-2)2+1=x2-x+2.
(2)以BD为直径作圆,圆心为点C,求证:圆C与x轴相切.
图Z7-34
(2)证明:解方程组
得
得到点B的坐标为(3-,),点D的坐标为(3+,).
∵点C是BD的中点,
∴点C的纵坐标为,
利用两点间距离公式,可算出BD==5.
∴圆C的半径r=,
∴圆心C到x轴的距离等于半径r,∴圆C与x轴相切.
(3)圆C与直线m交于抛物线的对称轴右侧的点M(t,1).直线m上每一点的纵坐标都等于1.过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F.求BE∶MF的值.
图Z7-34
(3)方法一:连接BM和DM,
∵BD为直径,∴∠BMD=90°,
∴∠BME+∠DMF=180°-90°=90°,
又∵BE⊥直线m于点E,DF⊥直线m于点F,
∴∠DMF+∠MDF=90°,
∴∠BME=∠MDF,∴△BME∽△MDF,
∴,
∵BE=,MF=3+-t,EM=t-(3-),DF=,
∴,
化简得(t-3)2=4,解得t=5或t=1,
抛物线的对称轴为直线x=2,
∵点M在对称轴右侧,∴t=5,∴.
方法二:如图,过点C作CH⊥直线m,垂足为H,连接CM,
由(2)知CM=r=,CH=r-1=,
在Rt△CHF中,由勾股定理,得MH==2,
又∵HF=,
∴MF=HF-MH=-2,
又∵BE=-1=,∴.
【方法点析】与圆有关的切线问题,可以转化为切点到圆心距离等于半径,或者转化为直角三角形问题,或者构造K字形找相似三角形来列方程.与圆有关的角度问题,可以考虑圆心角、圆周角的性质定理进行角度转换.
|题型精练|
[2021·张家界23题节选]如图Z7-35,已知二次函数y=ax2+bx+c的图象经过点C(2,-3),且与x轴交于原点及点B(8,0).
(1)求二次函数的表达式;
(2)求顶点A的坐标及直线AB的表达式;
(3)若点P为☉O上的动点,且☉O的半径为2,
一动点E从点A出发,以每秒2个单位长度的速度沿线段AP匀速运动到点P,再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动,求点E的运动时间t的最小值.
图Z7-35
(1)求二次函数的表达式;
图Z7-35
解:(1)根据题意得
解得
∴抛物线的解析式为y=x2-2x.
(2)求顶点A的坐标及直线AB的表达式;
图Z7-35
(2)∵y=x2-2x=(x2-8x+16-16)=(x-4)2-4,
∴二次函数图象的顶点A的坐标为(4,-4).
设直线AB的解析式为y=mx+n.
则有解得
∴直线AB的解析式为y=x-8.
(3)若点P为☉O上的动点,且☉O的半径为2,一动点E从点A出发,以每秒2个单位长度的速度沿线段AP匀速运动到点P,再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动,求点E的运动时间t的最小值.
图Z7-35
(3)如图,点P在以O为圆心,2为半径的圆周上.
依题意可知:动点E的运动时间t=AP+BP.
在OA上取Q使OQ=,连接PQ,PO.
∵OA==4,OP=2,∴,
∵∠POQ=∠AOP,∴△OQP∽△OPA,
∴,∴t=AP+BP=PQ+BP.
显然当B,P,Q三点共线时,PQ+BP取得最小值BQ.
过点Q作QH⊥OB于H.易得OA=AB=4,OB=8,
∴OA2+AB2=OB2,∴∠OAB=90°,
∴△ABO为等腰直角三角形,
∴∠AOB=45°,∴在Rt△OQH中,QH=OH=1,
∴BH=OB-OH=7,
∴BQ==5,
∴t的最小值为5.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
