人教版七年级下册9.1.2 不等式的性质课件(共20张PPT)
文档属性
| 名称 | 人教版七年级下册9.1.2 不等式的性质课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 08:44:19 | ||
图片预览






文档简介
(共20张PPT)
9.1.2 不等式的性质
请直接说出下列不等式的解集
你还能直接说出下面不等式的解集吗?
新课导入
探索新知
活动一:拿出准备的教具天平和砝码,放不同质量的砝码,会出现什么现象,在此基础上,两边同时增加或减少相同质量的砝码又会发生什么现象?小组实验讨论,得出结论
用“>”或 “ <”填空,并总结其中的规律。
,
(1) 5>3
(2) -1<3
知识讲解
>
>
<
<
如果
那么
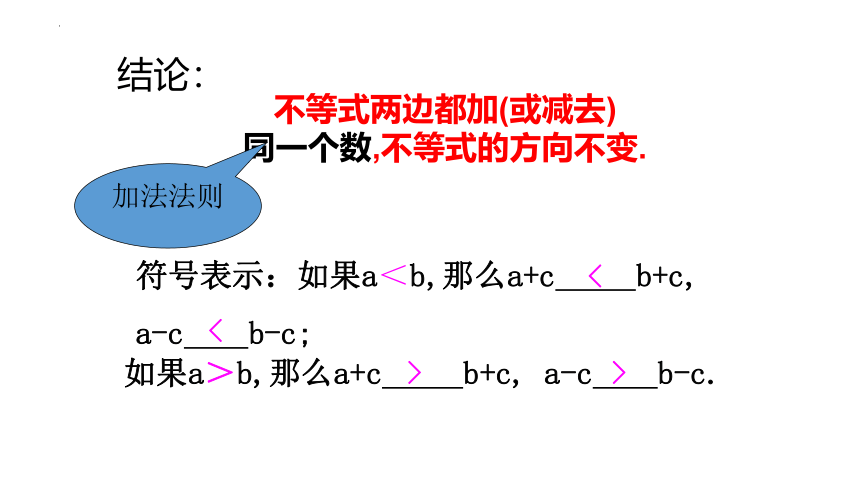
如果a>b,那么a+c b+c, a-c b-c.
符号表示:如果a<b,那么a+c b+c,
a-c b-c;
>
>
结论:
<
<
不等式两边都加(或减去)
同一个数,不等式的方向不变.
加法法则
活动二!
1、放不同质量的砝码在天平的两边,会有什么结果?
2、在此基础上,左右两边同时放入原砝码相同倍数质量的砝
码,观察又有什么现象发生?
3、如果,左右两边同时去掉相同倍数质量的砝码又
会怎样?
注:倍数指的是什么运算?
这里的倍数都是什么类型的数?
结论:
不等式两边同时乘(或除以)同一个正数,不等号方向不变;
符号表示:
如果a>b,c>0,那么ac>bc;
如果a>b,c>0,那么a/c>b/c
乘法法则
不等号方向改变吗
做一做
用“>”、 “<” 填空:
(4)6>2, 6×5 2×5,6÷ 5 2×5;
(5)-2<3, (-2)×6 3×6,(-2)÷6 3÷6;
(6) -2>-3, -2×2___-3×2,-2÷2____-3÷2.
>
>
<
<
>
>
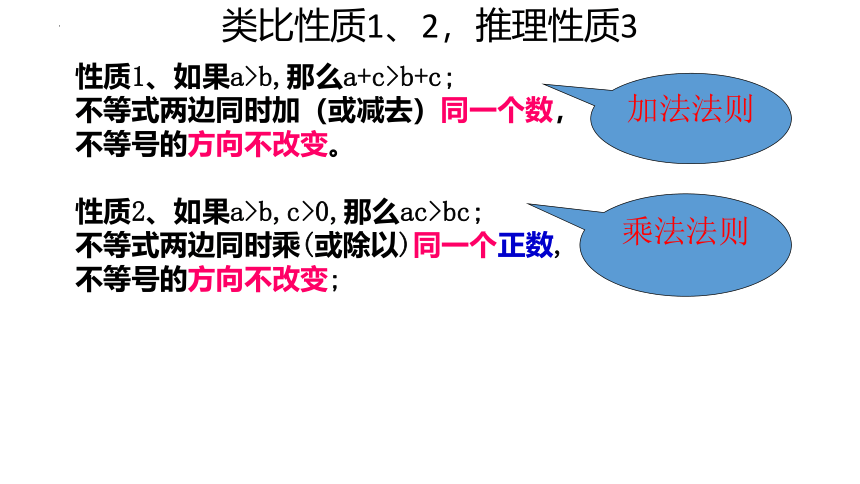
类比性质1、2,推理性质3
加法法则
性质1、如果a>b,那么a+c>b+c;
不等式两边同时加(或减去)同一个数,
不等号的方向不改变。
性质2、如果a>b,c>0,那么ac>bc;
不等式两边同时乘(或除以)同一个正数,
不等号的方向不改变;
乘法法则
活动三:
问题1:如果李国林同学刚才有的钱数350元和贾玉琛同学的钱变为欠的钱了会有什么情况发生?
问题2:如果1<2,那么两边同时乘以-1会有什么情况发生?试用数轴比较出大小。
问题3:如果2<3,那么左右两边同除以-1会有什么情况发生?用数轴表示数比较出大小。
小组讨论,得出结果
完成下列填空:
2<3 2X5 ____ 3X5
2<3 2X0.5 ____3X0.5
2<3 2X(-1)____3X(-1)
2<3 2X(-5)____3X(-5)
2<3 2X(-0.5)_____ 3X(-0.5)
你发现了什么?
<
<
>
>
>
做一做
同乘正数
同乘负数
方向不变
方向改变
符号表示:
如果a>b,c<0,那么ac结论:
不等式两边都乘(或除以)同一个负数,不等号要改变方向.
有理数乘法
不等式,性质三;
同加同减号不变;
同乘同除且放慢,
同正不变同负变!
口诀:
例1:利用不等式的性质解下列不等式并用数轴表示解集。
(1)x-7>26 (2) 3x<2x-3
(3) (4) -4x>3
例题讲解
(1) x-7>26
解:根据不等式性质1,得
x-7+7>26+7
x>33
这个不等式的解集在数轴的表示如图
33
0
(2) 3x<2x-3
解:根据不等式的性质1,得
3x-2x<2x-3-2x
x<-3
-3
(4) -4x>3
解:根据不等式性质3,得
即
不等式的解集在数轴上的表示如图
1.设a>b,用“>,<”填空,并说明依据不等式的哪条性质;
课堂练习
>
>
>
<
<
2.填一填
(1)若x+1>0,两边同加上-1,得____ (依据什么?)
(2)若2x>-6, 两边同除以2, 得____ (依据什么?)
(3)若-3x<6, 两边同除以-3, 得____(依据什么?)
课堂练习
x>-1
x>-3
x>-2
【课堂小结】
课堂小结
1、本节课重点:
(1)掌握不等式的三条基本性质,尤其是性质3。
(2)能正确应用性质对不等式进行变形。
2、注意事项:
当不等式的两边乘(或除以)同一个数时,一定要看清楚是正数还是负数。
9.1.2 不等式的性质
请直接说出下列不等式的解集
你还能直接说出下面不等式的解集吗?
新课导入
探索新知
活动一:拿出准备的教具天平和砝码,放不同质量的砝码,会出现什么现象,在此基础上,两边同时增加或减少相同质量的砝码又会发生什么现象?小组实验讨论,得出结论
用“>”或 “ <”填空,并总结其中的规律。
,
(1) 5>3
(2) -1<3
知识讲解
>
>
<
<
如果
那么
如果a>b,那么a+c b+c, a-c b-c.
符号表示:如果a<b,那么a+c b+c,
a-c b-c;
>
>
结论:
<
<
不等式两边都加(或减去)
同一个数,不等式的方向不变.
加法法则
活动二!
1、放不同质量的砝码在天平的两边,会有什么结果?
2、在此基础上,左右两边同时放入原砝码相同倍数质量的砝
码,观察又有什么现象发生?
3、如果,左右两边同时去掉相同倍数质量的砝码又
会怎样?
注:倍数指的是什么运算?
这里的倍数都是什么类型的数?
结论:
不等式两边同时乘(或除以)同一个正数,不等号方向不变;
符号表示:
如果a>b,c>0,那么ac>bc;
如果a>b,c>0,那么a/c>b/c
乘法法则
不等号方向改变吗
做一做
用“>”、 “<” 填空:
(4)6>2, 6×5 2×5,6÷ 5 2×5;
(5)-2<3, (-2)×6 3×6,(-2)÷6 3÷6;
(6) -2>-3, -2×2___-3×2,-2÷2____-3÷2.
>
>
<
<
>
>
类比性质1、2,推理性质3
加法法则
性质1、如果a>b,那么a+c>b+c;
不等式两边同时加(或减去)同一个数,
不等号的方向不改变。
性质2、如果a>b,c>0,那么ac>bc;
不等式两边同时乘(或除以)同一个正数,
不等号的方向不改变;
乘法法则
活动三:
问题1:如果李国林同学刚才有的钱数350元和贾玉琛同学的钱变为欠的钱了会有什么情况发生?
问题2:如果1<2,那么两边同时乘以-1会有什么情况发生?试用数轴比较出大小。
问题3:如果2<3,那么左右两边同除以-1会有什么情况发生?用数轴表示数比较出大小。
小组讨论,得出结果
完成下列填空:
2<3 2X5 ____ 3X5
2<3 2X0.5 ____3X0.5
2<3 2X(-1)____3X(-1)
2<3 2X(-5)____3X(-5)
2<3 2X(-0.5)_____ 3X(-0.5)
你发现了什么?
<
<
>
>
>
做一做
同乘正数
同乘负数
方向不变
方向改变
符号表示:
如果a>b,c<0,那么ac
不等式两边都乘(或除以)同一个负数,不等号要改变方向.
有理数乘法
不等式,性质三;
同加同减号不变;
同乘同除且放慢,
同正不变同负变!
口诀:
例1:利用不等式的性质解下列不等式并用数轴表示解集。
(1)x-7>26 (2) 3x<2x-3
(3) (4) -4x>3
例题讲解
(1) x-7>26
解:根据不等式性质1,得
x-7+7>26+7
x>33
这个不等式的解集在数轴的表示如图
33
0
(2) 3x<2x-3
解:根据不等式的性质1,得
3x-2x<2x-3-2x
x<-3
-3
(4) -4x>3
解:根据不等式性质3,得
即
不等式的解集在数轴上的表示如图
1.设a>b,用“>,<”填空,并说明依据不等式的哪条性质;
课堂练习
>
>
>
<
<
2.填一填
(1)若x+1>0,两边同加上-1,得____ (依据什么?)
(2)若2x>-6, 两边同除以2, 得____ (依据什么?)
(3)若-3x<6, 两边同除以-3, 得____(依据什么?)
课堂练习
x>-1
x>-3
x>-2
【课堂小结】
课堂小结
1、本节课重点:
(1)掌握不等式的三条基本性质,尤其是性质3。
(2)能正确应用性质对不等式进行变形。
2、注意事项:
当不等式的两边乘(或除以)同一个数时,一定要看清楚是正数还是负数。
