沪科版七年级下册9.3 分式方程课件(共32张PPT)
文档属性
| 名称 | 沪科版七年级下册9.3 分式方程课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 685.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 07:05:50 | ||
图片预览










文档简介
(共32张PPT)
第2课时 分式方程的应用
沪科版数学七年级下册
9.3 分式方程
第9章 分式
教学目标
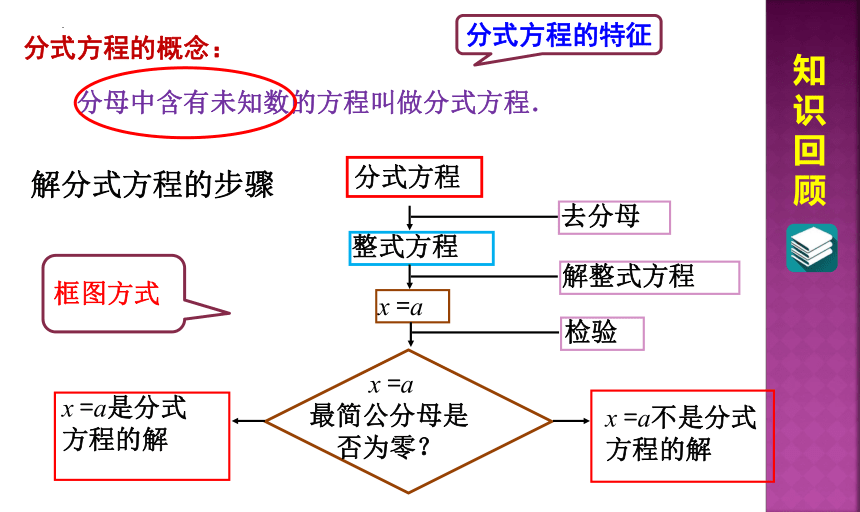
分式方程的概念:
分母中含有未知数的方程叫做分式方程.
知识回顾
分式方程的特征
解分式方程的步骤
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
框图方式
1、把分式方程化为整式方程,若整式方程无解,则分式方 程一定______;若整式方程有解,但要使分式方程无解,则该解必是 ______.
填一填
知识回顾
无解
增根
2、增根的产生的原因:在分式方程变形为整式方程时,方程两边同乘以一个含________的整式(最简公分母可能是“隐形”的______),并约去了分母,有时可能产生不适合原方程的解(或根),这种根称为增根.因此,在解分式方程时必须进行________.
未知数
零
检验
4、增根的应用:运用增根的这两个特征,可以简捷地确定分式方程中的参数(字母系数)的值.解这类题的一般步骤:
①把分式方程化成的________方程;
②令公分母为______,求出x的值;
③再把x的值代入_______方程,求出字母系数的值.
填一填
知识回顾
3、分式方程的增根的条件有两个:
①它是_______后所得______方程的根;
②它应使____________的值为零.
最简公分母
整式
去分母
整式
零
整式
若方程 会产生增根,
则( )
A、k=±2 B、k=2
C、k=-2 D、k为任何实数
巩固练习
去分母:x-2-k(x+2)=(x-2)(x+2)-4x
令x -4=0
X=±2
把x=2带入整式方程得k=2
把x=-2带入整式方程得k无解
B
解析:
(一)解含字母系数的分式方程
分式方程的应用
讲授新知
例1 解关于x 的方程+b=1(b≠1)
解:
方程两边同乘(x-a),得:
a+b(x-a) =x-a
a+bx-ab=x-a
bx-x=-a-a+ab
(b-1)x=ab-2a
∵b≠1 ∴b-1 ≠0
∴x=
检验:
当 x=
∴x= 是原分式方程的解.
原分式方程的解:
x=
例题讲解
课堂练习
解关于x 的方程, =0(n≠m≠0)
练一练
解:
方程两边同乘x(x+1),得:
m(x+1)-nx=0
(m-n)x= - m
∵ n≠m≠0
∴m-n ≠0
∴x= -
检验:
当 x= -
∴ x= - 是原分式方程的解
原分式方程的解:
x= -
分式方程的应用
(二)列分式方程解应用题
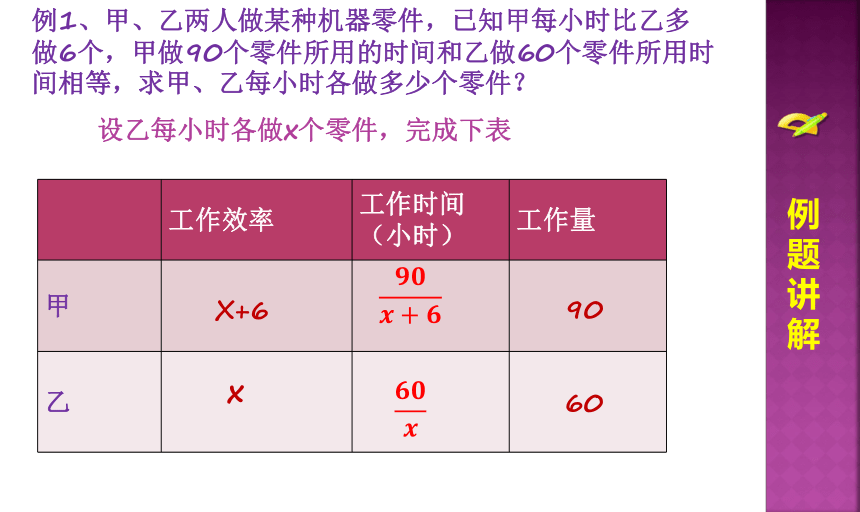
例1、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?
讨论
问题1:问题中未知量是什么
甲、乙每小时各做多少个零件
问题2:问题中相等关系是什么
甲的工作效率=乙的工作效率+6
甲做90个零件所用的时间=乙做60个零件所用时间
例题讲解
设乙每小时各做x个零件,完成下表
工作效率 工作时间(小时) 工作量
甲
乙
x
X+6
90
60
例题讲解
例1、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?
例1、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?
解:设乙每小时做x个零件, 依题意得:
=
90x=60x+360
30x=360
X=12
经检验X=12是原方程的根,且符合题意。
答:甲每小时做18个,乙每小时12个
∴x+6=18
结果一定要检验
例题讲解
例2、某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
工作效率 工作时间(小时) 工作量
甲队
乙队
设规定日期是x天,完成下表
相等关系:
甲队工作量+乙队工作量=总工作量1
例题讲解
例2、某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
解;设规定日期是x天,根据题意,得:
方程两边同乘以x(x+3),得:
2(x+3)+x2=x(x+3)
解得: x=6
检验:
当x=6时x(x+3)≠0,
∴x=6是原方程的解。
答:规定日期是6天。
例题讲解
总结:列分式方程解应用题的方法和步骤如下:
1:审题分析题意
2:设未知数
3:根据题意找相等关系,列出方程;
4:解方程,并验根(对解分式方程尤为重要)
5:写答案
新知讲解
例3、 某次军事演习中,红队要到某桥头阻击蓝队,出发时蓝队离桥头24Km,红队离桥头30Km,红队急行军速度是蓝队的1.5倍,结果比蓝队提前48分钟到达,求红队急行军的速度。
例题讲解
设蓝队的速度为X千米/时
路程 速度 时间(小时)
蓝队
红队
24
30
x
1.5 x
等量关系:
红队的时间= 蓝队的时间 -
例3、 某次军事演习中,红队要到某桥头阻击蓝队,出发时蓝队离桥头24Km,红队离桥头30Km,红队急行军速度是蓝队的1.5倍,结果比蓝队提前48分钟到达,求红队急行军的速度。
解:设蓝队的速度为X千米/时,则红队为1.5X千米/时。
由题意得方程:
解方程得:x=5
经检验x=5符合题意
∴1.5x=7.5(千米/时)
答:红队急行军的速度是7.5千米/小时。
例题讲解
设元时单位一定要统一
(1)把公式 变为已知f、v,求u 的公式。
练习1:
课堂练习
解:
uv fu
去分母得:
uv-
(v-f)u
∴ u
∵v-f≠0
(2)已知商品的买入价为a,售出价为b,毛利率p= (b>a)把这个分式变形成已知p、b,求a的分式。
解:
去分母得:
课堂练习
pa
pa
(p+1)a
∴ a
∵p+1≠0
1、某进货员发现一种应季衬衫,预计能畅销,他用8 000元购进一批衬衫,很快销售一空.再进货时,他发现这种衬衫的单价比上一次贵了4 元/件,他用17 600元购进2 倍于第一次进货量的这种衬衫.问第一次购进多少件衬衫?
练习2
课堂练习
进货数量 (件) 进货总价(元) 进货单价(元/件)
第一次
第二次
x
2x
8 000
17 600
设第一次购进x件衬衫
去分母得: 17 600-16 000 =8x
解得 x =200
解:设第一次购进x件衬衫,由题意得,
检验:当x =200时,2x =400≠0,
所以,x =200是原分式方程的解,且符合题意.
答:第一次购进200件衬衫.
课堂练习
1、某进货员发现一种应季衬衫,预计能畅销,他用8 000元购进一批衬衫,很快销售一空.再进货时,他发现这种衬衫的单价比上一次贵了4 元/件,他用17 600元购进2 倍于第一次进货量的这种衬衫.问第一次购进多少件衬衫?
2、 某商店用80000元购进一批时装,以58元/件销售,结果供不应求.然后又用176000元购进数量是第一次的2倍,单价比第一次贵4元的同样的时装继续销售,最后剩下150件按八折销售完毕.问这批服装一共有多少件?该商店这笔生意是盈还是亏,是多少?
变 式
课堂练习
解:设这批时装进价为x元/件,由题意得:
=2×
解得x=40,
∴第一次购进=2000(件),
第二次购进=4000(件).
共盈利:
(6000-150)×58+150×58×0.8-80000-176000= 90260
练习2
3、一轮船往返于A、B两地之间,顺水比逆水快1小时到达。已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度。
速度(千米/小时) 时间(小时) 路程(千米)
顺水
逆水
设:轮船在静水中的速度是X千米/小时。
等量关系:逆水所需时间-顺水所需时间=1(小时)
X+2
X-2
80
80
80
X-2
-
80
X+2
=
1
课堂练习
练习2
3、一轮船往返于A、B两地之间,顺水比逆水快1小时到达。已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度。
X=-18(不合题意,舍去)
80
X-2
-
80
X+2
=
1
解:设船在静水中的速度为X千米/小时。
X2=324
80X+160 -80X+160=X2 -4
X=±18
检验得: X=18
答:船在静水中的速度为18千米/小时。
课堂练习
练习2
利用平方根定义求出x
4、工厂生产一种电子配件,每只成本为2元,利润率为25%.后来通过工艺改进,降低成本,在售价不变的情况下,利润率增加了75%.问这种配件每只的成本降低了多少
提升练习
练习3
等量关系:现利润率=原利润率+75%
成本 售价 利润 利润率
原来
现在
设这种配件每只的成本降低了x元,
2
2-x
2×(1+25%)=2.5
2×(1+25%)=2.5
2×25%
25%
2.5-(2-x)
解:设这种配件每只的成本降低了x元,由题意得
4、工厂生产一种电子配件,每只成本为2元,利润率为25%.后来通过工艺改进,降低成本,在售价不变的情况下,利润率增加了75%.问这种配件每只的成本降低了多少
整理方程得:
解方程得: x=0.75
= 1
经检验,x= 0.75 是原方程的根
答这种配件每只的成本降低了 0.75 元。
提升练习
练习3
工厂生产一种电子配件,每只成本为2元,利率为25%.后来通过工艺改进,降低成本,在售价不变的情况下,利率增加了75%.问这种配件每只的成本降低了多少
等量关系:原售价=现售价
现售价=现成本(1+现利率)
原售价=原成本(1+原利率)
解:设这种配件每只的成本降低了x元,由题意得:
答这种配件每只的成本降低了 0.75 元。
2×(1+25%)=(2-x)(1+25%+75%)
解方程得: x=0.75
一题多解
分析:
某列车行驶速度平均s千米∕小时,现经改良,平均提速v千米∕小时,用相同的时间,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?
提速前列车行驶s千米所用的时间为 小时,
提速后列车的平均速度为 千米∕小时,
提速后列车运行(s+50)千米所用的时间为 小时。
(x+v)
拓展练习
练习4
等量关系:
提速前列车行驶s千米所用的时间=提速后列车运行(s+50)千米所用的时间
某列车行驶速度平均s千米∕小时,现经改良,平均提速v千米∕小时,用相同的时间,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?
解:设提速前这次列车的平均速度为x千米∕小时
方程两边同乘以x(x+v),得:
s(x+v)=x(s+50)
解得:
检验:由于v,s都是正数
x(x+v)≠0,
是原方程的解。
时
答:千米/小时
总结:
1、列分式方程解应用题,应该注意解题的五个步骤。
2、列方程的关键是要在准确设元(可直接设,也可间节设)的前提下找出等量关系。
3、解题过程注意画图或列表帮助分析题意找等量关系。
4、注意不要漏检验和写答案。
请同学总结该节课学习的内容
课堂总结
1、某农场开挖一条长960米的渠道,开工后工作效率比计划提高50%,结果提前4天完成任务。原计划每天挖多少米?
课后练习
2、两个工程队共同参与一项筑路工程,甲队单独施工一个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成. 哪个队的施工速度快?
3、若R+ =s,求n
解:
设乙队如果单独施工一个月能完成总工程的 .
= 1
解:设原计划每天挖x米
X=80(米)
n=
X=1
乙队的施工速度快
第2课时 分式方程的应用
沪科版数学七年级下册
9.3 分式方程
第9章 分式
教学目标
分式方程的概念:
分母中含有未知数的方程叫做分式方程.
知识回顾
分式方程的特征
解分式方程的步骤
分式方程
整式方程
去分母
解整式方程
x =a
检验
x =a是分式
方程的解
x =a不是分式
方程的解
x =a
最简公分母是
否为零?
框图方式
1、把分式方程化为整式方程,若整式方程无解,则分式方 程一定______;若整式方程有解,但要使分式方程无解,则该解必是 ______.
填一填
知识回顾
无解
增根
2、增根的产生的原因:在分式方程变形为整式方程时,方程两边同乘以一个含________的整式(最简公分母可能是“隐形”的______),并约去了分母,有时可能产生不适合原方程的解(或根),这种根称为增根.因此,在解分式方程时必须进行________.
未知数
零
检验
4、增根的应用:运用增根的这两个特征,可以简捷地确定分式方程中的参数(字母系数)的值.解这类题的一般步骤:
①把分式方程化成的________方程;
②令公分母为______,求出x的值;
③再把x的值代入_______方程,求出字母系数的值.
填一填
知识回顾
3、分式方程的增根的条件有两个:
①它是_______后所得______方程的根;
②它应使____________的值为零.
最简公分母
整式
去分母
整式
零
整式
若方程 会产生增根,
则( )
A、k=±2 B、k=2
C、k=-2 D、k为任何实数
巩固练习
去分母:x-2-k(x+2)=(x-2)(x+2)-4x
令x -4=0
X=±2
把x=2带入整式方程得k=2
把x=-2带入整式方程得k无解
B
解析:
(一)解含字母系数的分式方程
分式方程的应用
讲授新知
例1 解关于x 的方程+b=1(b≠1)
解:
方程两边同乘(x-a),得:
a+b(x-a) =x-a
a+bx-ab=x-a
bx-x=-a-a+ab
(b-1)x=ab-2a
∵b≠1 ∴b-1 ≠0
∴x=
检验:
当 x=
∴x= 是原分式方程的解.
原分式方程的解:
x=
例题讲解
课堂练习
解关于x 的方程, =0(n≠m≠0)
练一练
解:
方程两边同乘x(x+1),得:
m(x+1)-nx=0
(m-n)x= - m
∵ n≠m≠0
∴m-n ≠0
∴x= -
检验:
当 x= -
∴ x= - 是原分式方程的解
原分式方程的解:
x= -
分式方程的应用
(二)列分式方程解应用题
例1、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?
讨论
问题1:问题中未知量是什么
甲、乙每小时各做多少个零件
问题2:问题中相等关系是什么
甲的工作效率=乙的工作效率+6
甲做90个零件所用的时间=乙做60个零件所用时间
例题讲解
设乙每小时各做x个零件,完成下表
工作效率 工作时间(小时) 工作量
甲
乙
x
X+6
90
60
例题讲解
例1、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?
例1、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件?
解:设乙每小时做x个零件, 依题意得:
=
90x=60x+360
30x=360
X=12
经检验X=12是原方程的根,且符合题意。
答:甲每小时做18个,乙每小时12个
∴x+6=18
结果一定要检验
例题讲解
例2、某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
工作效率 工作时间(小时) 工作量
甲队
乙队
设规定日期是x天,完成下表
相等关系:
甲队工作量+乙队工作量=总工作量1
例题讲解
例2、某工程队需要在规定日期内完成。若甲队单独做正好按时完成;若乙队单独做,超过规定日期三天才能完成。现由甲、乙合作两天,余下工程由乙队单独做,恰好按期完成,问规定日期是多少天?
解;设规定日期是x天,根据题意,得:
方程两边同乘以x(x+3),得:
2(x+3)+x2=x(x+3)
解得: x=6
检验:
当x=6时x(x+3)≠0,
∴x=6是原方程的解。
答:规定日期是6天。
例题讲解
总结:列分式方程解应用题的方法和步骤如下:
1:审题分析题意
2:设未知数
3:根据题意找相等关系,列出方程;
4:解方程,并验根(对解分式方程尤为重要)
5:写答案
新知讲解
例3、 某次军事演习中,红队要到某桥头阻击蓝队,出发时蓝队离桥头24Km,红队离桥头30Km,红队急行军速度是蓝队的1.5倍,结果比蓝队提前48分钟到达,求红队急行军的速度。
例题讲解
设蓝队的速度为X千米/时
路程 速度 时间(小时)
蓝队
红队
24
30
x
1.5 x
等量关系:
红队的时间= 蓝队的时间 -
例3、 某次军事演习中,红队要到某桥头阻击蓝队,出发时蓝队离桥头24Km,红队离桥头30Km,红队急行军速度是蓝队的1.5倍,结果比蓝队提前48分钟到达,求红队急行军的速度。
解:设蓝队的速度为X千米/时,则红队为1.5X千米/时。
由题意得方程:
解方程得:x=5
经检验x=5符合题意
∴1.5x=7.5(千米/时)
答:红队急行军的速度是7.5千米/小时。
例题讲解
设元时单位一定要统一
(1)把公式 变为已知f、v,求u 的公式。
练习1:
课堂练习
解:
uv fu
去分母得:
uv-
(v-f)u
∴ u
∵v-f≠0
(2)已知商品的买入价为a,售出价为b,毛利率p= (b>a)把这个分式变形成已知p、b,求a的分式。
解:
去分母得:
课堂练习
pa
pa
(p+1)a
∴ a
∵p+1≠0
1、某进货员发现一种应季衬衫,预计能畅销,他用8 000元购进一批衬衫,很快销售一空.再进货时,他发现这种衬衫的单价比上一次贵了4 元/件,他用17 600元购进2 倍于第一次进货量的这种衬衫.问第一次购进多少件衬衫?
练习2
课堂练习
进货数量 (件) 进货总价(元) 进货单价(元/件)
第一次
第二次
x
2x
8 000
17 600
设第一次购进x件衬衫
去分母得: 17 600-16 000 =8x
解得 x =200
解:设第一次购进x件衬衫,由题意得,
检验:当x =200时,2x =400≠0,
所以,x =200是原分式方程的解,且符合题意.
答:第一次购进200件衬衫.
课堂练习
1、某进货员发现一种应季衬衫,预计能畅销,他用8 000元购进一批衬衫,很快销售一空.再进货时,他发现这种衬衫的单价比上一次贵了4 元/件,他用17 600元购进2 倍于第一次进货量的这种衬衫.问第一次购进多少件衬衫?
2、 某商店用80000元购进一批时装,以58元/件销售,结果供不应求.然后又用176000元购进数量是第一次的2倍,单价比第一次贵4元的同样的时装继续销售,最后剩下150件按八折销售完毕.问这批服装一共有多少件?该商店这笔生意是盈还是亏,是多少?
变 式
课堂练习
解:设这批时装进价为x元/件,由题意得:
=2×
解得x=40,
∴第一次购进=2000(件),
第二次购进=4000(件).
共盈利:
(6000-150)×58+150×58×0.8-80000-176000= 90260
练习2
3、一轮船往返于A、B两地之间,顺水比逆水快1小时到达。已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度。
速度(千米/小时) 时间(小时) 路程(千米)
顺水
逆水
设:轮船在静水中的速度是X千米/小时。
等量关系:逆水所需时间-顺水所需时间=1(小时)
X+2
X-2
80
80
80
X-2
-
80
X+2
=
1
课堂练习
练习2
3、一轮船往返于A、B两地之间,顺水比逆水快1小时到达。已知A、B两地相距80千米,水流速度是2千米/小时,求轮船在静水中的速度。
X=-18(不合题意,舍去)
80
X-2
-
80
X+2
=
1
解:设船在静水中的速度为X千米/小时。
X2=324
80X+160 -80X+160=X2 -4
X=±18
检验得: X=18
答:船在静水中的速度为18千米/小时。
课堂练习
练习2
利用平方根定义求出x
4、工厂生产一种电子配件,每只成本为2元,利润率为25%.后来通过工艺改进,降低成本,在售价不变的情况下,利润率增加了75%.问这种配件每只的成本降低了多少
提升练习
练习3
等量关系:现利润率=原利润率+75%
成本 售价 利润 利润率
原来
现在
设这种配件每只的成本降低了x元,
2
2-x
2×(1+25%)=2.5
2×(1+25%)=2.5
2×25%
25%
2.5-(2-x)
解:设这种配件每只的成本降低了x元,由题意得
4、工厂生产一种电子配件,每只成本为2元,利润率为25%.后来通过工艺改进,降低成本,在售价不变的情况下,利润率增加了75%.问这种配件每只的成本降低了多少
整理方程得:
解方程得: x=0.75
= 1
经检验,x= 0.75 是原方程的根
答这种配件每只的成本降低了 0.75 元。
提升练习
练习3
工厂生产一种电子配件,每只成本为2元,利率为25%.后来通过工艺改进,降低成本,在售价不变的情况下,利率增加了75%.问这种配件每只的成本降低了多少
等量关系:原售价=现售价
现售价=现成本(1+现利率)
原售价=原成本(1+原利率)
解:设这种配件每只的成本降低了x元,由题意得:
答这种配件每只的成本降低了 0.75 元。
2×(1+25%)=(2-x)(1+25%+75%)
解方程得: x=0.75
一题多解
分析:
某列车行驶速度平均s千米∕小时,现经改良,平均提速v千米∕小时,用相同的时间,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?
提速前列车行驶s千米所用的时间为 小时,
提速后列车的平均速度为 千米∕小时,
提速后列车运行(s+50)千米所用的时间为 小时。
(x+v)
拓展练习
练习4
等量关系:
提速前列车行驶s千米所用的时间=提速后列车运行(s+50)千米所用的时间
某列车行驶速度平均s千米∕小时,现经改良,平均提速v千米∕小时,用相同的时间,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?
解:设提速前这次列车的平均速度为x千米∕小时
方程两边同乘以x(x+v),得:
s(x+v)=x(s+50)
解得:
检验:由于v,s都是正数
x(x+v)≠0,
是原方程的解。
时
答:千米/小时
总结:
1、列分式方程解应用题,应该注意解题的五个步骤。
2、列方程的关键是要在准确设元(可直接设,也可间节设)的前提下找出等量关系。
3、解题过程注意画图或列表帮助分析题意找等量关系。
4、注意不要漏检验和写答案。
请同学总结该节课学习的内容
课堂总结
1、某农场开挖一条长960米的渠道,开工后工作效率比计划提高50%,结果提前4天完成任务。原计划每天挖多少米?
课后练习
2、两个工程队共同参与一项筑路工程,甲队单独施工一个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成. 哪个队的施工速度快?
3、若R+ =s,求n
解:
设乙队如果单独施工一个月能完成总工程的 .
= 1
解:设原计划每天挖x米
X=80(米)
n=
X=1
乙队的施工速度快
