沪科版数学七年级下册 10.3平行线的性质(第1课时平行线性质)课件(共26张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.3平行线的性质(第1课时平行线性质)课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 794.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 00:00:00 | ||
图片预览



文档简介
(共26张PPT)
沪科版数学七年级下册
10.3 平行线的性质
第一课时
学习目标
2
3
1
掌握平行线的性质定理,理解它们的图形语言、文字语言、符号语言以及它们之间的转换
会用平行线的性质进行简单的计算和说理,体会几何中图形之间的“位置关系”与“数量关系”有内在 联系
经历探索平行线的性质的过程,让学生树立科学态度,学习探究方法
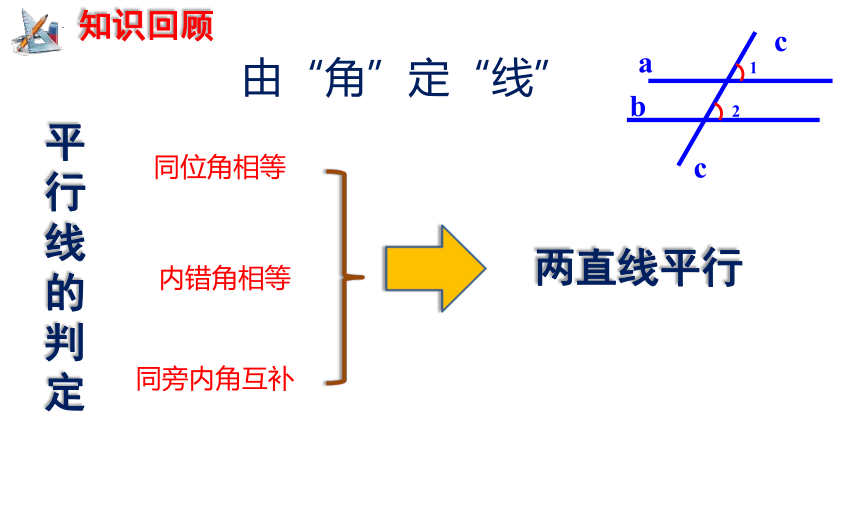
知识回顾
b
1
2
a
c
c
平行线的判定
两直线平行
同位角相等
内错角相等
同旁内角互补
由“角”定“线”
同位角相等
两直线平行
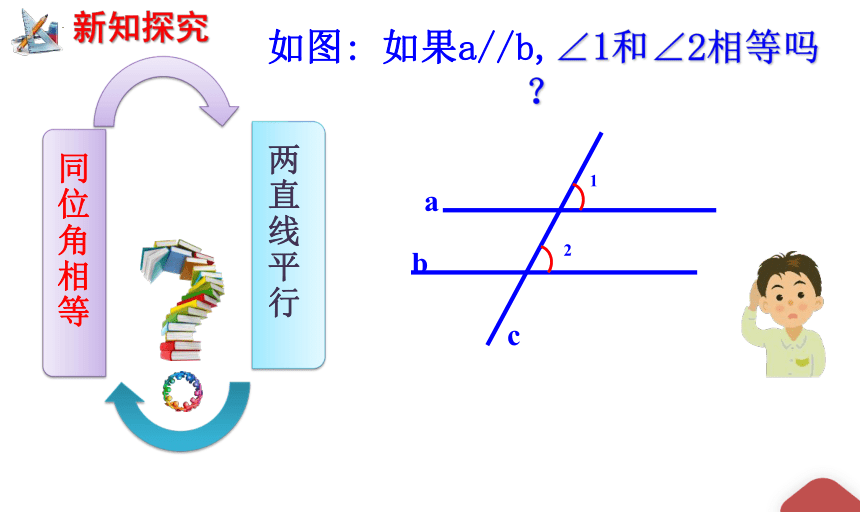
新知探究
如图: 如果a//b,∠1和∠2相等吗?
b
1
2
a
c
A
C
E
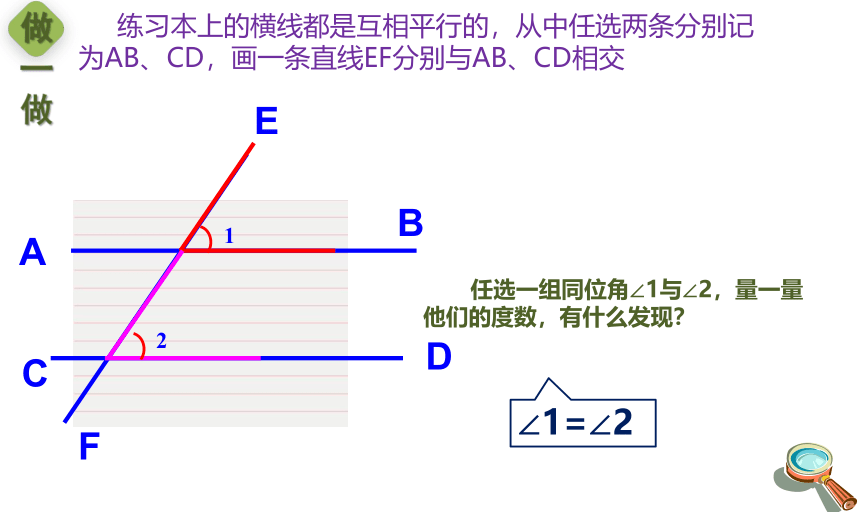
做一做
练习本上的横线都是互相平行的,从中任选两条分别记为AB、CD,画一条直线EF分别与AB、CD相交
B
D
F
任选一组同位角∠1与∠2,量一量他们的度数,有什么发现?
1
2
∠1=∠2
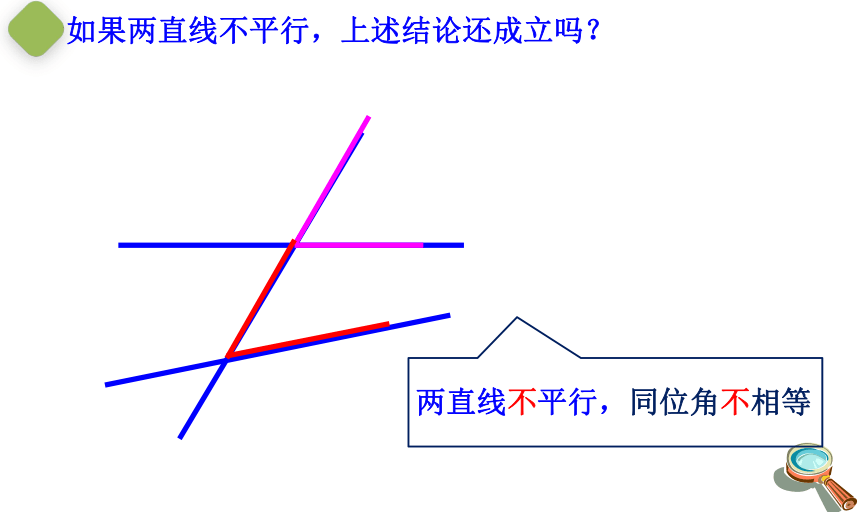
如果两直线不平行,上述结论还成立吗?
两直线不平行,同位角不相等
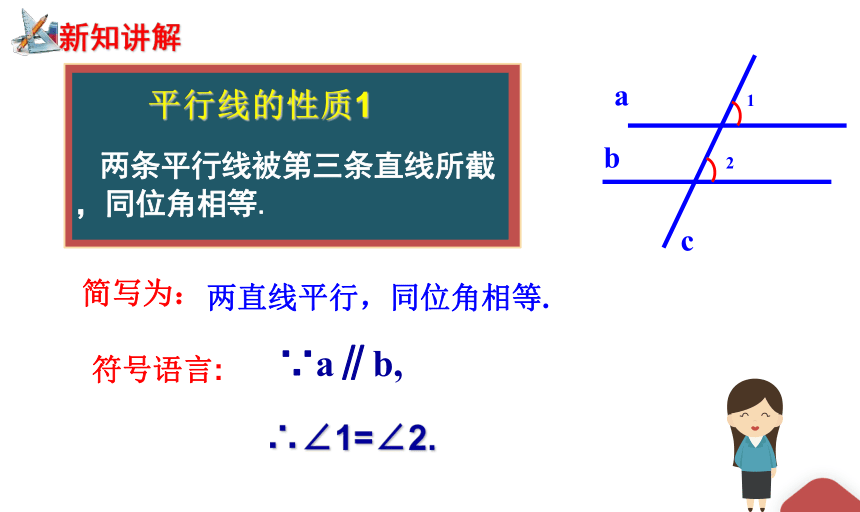
两直线平行,同位角相等.
平行线的性质1
两条平行线被第三条直线所截,同位角相等.
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
新知讲解
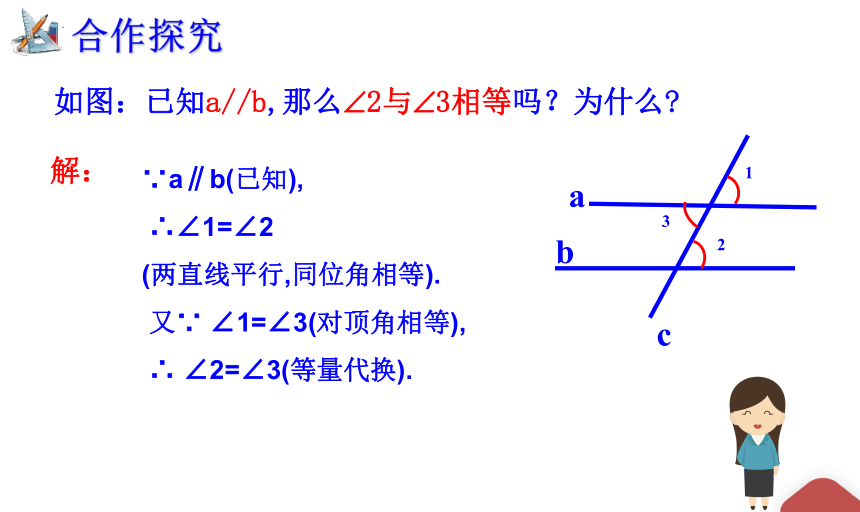
如图:已知a//b,那么 2与 3相等吗?为什么
∵a∥b(已知),
∴∠1=∠2
(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
合作探究
解:
两直线平行,内错角相等.
平行线的性质2
两条平行线被第三条直线所截,内错角相等.
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
新知讲解
解: ∵a//b (已知)
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
∴ 1= 2(两直线平行,同位角相等)
∵ 1+ 4=180°(邻补角定义)
∴ 2+ 4=180°(等量代换).
合作探究
你能用一句话表述这个现象吗?
两直线平行,同旁内角互补.
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
∴ 2+ 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
新知讲解
整理归纳
平行线的性质
b
1
2
a
c
4
性质1:两直线平行,同位角相等.
∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
性质2:两直线平行,内错角相等.
∵ a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补.
∵ a∥b( 已知 )
∴ ∠1+∠4=180° (两直线平行,同旁内角互补)
两直线平行
同旁内角互补
先知道线的位置关系
后知道角的大小关系
同位角相等
内错角相等
整理归纳
由“线”定“角”
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
判定
判定
判定
性质
性质
性质
整理归纳
平行线的性质与判定的区别
(1)已知∠3 =∠4,∠1=47°,求∠2的度数。
∴∠ 2= ( )
∵ ∠3 =∠4( )
∴a∥ ( )
又∵∠ 1 = 470 ( )
c
1
2
3
4
a
b
d
两直线平行,同位角相等
同位角相等,两直线平行
已知
已知
解:
练一练
完成下列填空
b
470
(2)如图,已知AB∥CD,AC∥BD,∠C= 39°,∠B和∠D是多少度?
1
A
C
B
D
E
解:
练一练
完成下列填空
∵AB∥CD( )
∴∠1=∠ = ° .
( )
C
∵ AC∥BD ,
∴∠B=∠ = °
( )
1
∴∠C+∠ =180°
( )
∴∠D= .
已知
39
两直线平行,同位角相等
39
两直线平行,内错角相等
D
两直线平行,同旁内角互补
141
例1、如图,DA⊥CE于点A,CD∥AB,∠1=30°,求∠D的度数
典例示范
A
C
B
D
E
┓
1
∵DA⊥CE(已知)
∴∠DAE=90°(垂直定义)
∵∠EAB=30°(已知)
∴∠BAD=60°
∵AB∥CD(已知)
∴∠D=∠BAD=60°
(两直线平行。内错角相等)
解:
例3、如图,∠B=80°, ∠CAF =50°,AC平分∠BAF, ,求∠C的度数
A
C
B
F
E
80°
典例示范
解:
∴EF∥BC
(同旁内角互补,两直线平行)
∵AC平分∠BAF( 已知)
∴∠BAF=2 ∠CAF (角平分线定义)
∵∠CAF =50°(已知)
∴∠BAF=2×50°=100°
∵∠B=80°(已知)
∴∠BAF+∠B=100°+80°=180°
∴∠C=∠CAF=50°
(两直线平行,内错角相等)
课堂练习
1、如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180° D.∠3+∠4=180°
D
1
2
3
4
A
B
C
B
1
选一选
课堂练习
1
选一选
2、如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )
A
C
B
D
┓
B
A.40° B.50° C.60° D.70°
课堂练习
1
选一选
3、如图,直线a∥b,直线c分别与a,b相交于A,B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
A
C
B
a
b
c
2
1
A.38° B.42°
C.48° D.58°
C
课堂练习
2
填一填
1、如图,已知AB//CD,AD//BC.填空:
(1)∵ AB//CD (已知),
∴ ∠1= ∠ ;
( );
(2) ∵ AD//BC (已知)
∴ ∠2= ∠___ 。
( ).
1
A
C
B
D
2
两直线平行,内错角相等.
两直线平行,内错角相等.
D
ACB
A
D
C
B
1、已知,如图,AB∥CD,∠B=∠D,求证:AD∥BC.
证明:
∵AB∥DC(已知)
∴∠B+∠C=180°
(两直线平行,同旁内角互补)
∵∠B=∠D(已知)
∴∠D+∠C=180°(等量代换)
∴AD∥BC(同旁内角互补,两直线平行)
拓展练习
3
证一证
解:∵AB//CD (已知)
∴∠C=∠1 ( )
又∵∠A=∠C(已知)
∴∠A= ( )
∴AE//FC
( )
∴∠E=∠F( )
A
D
E
C
B
F
两直线平行,同位角相等
∠1
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
2、如图,已知AB//CD,∠A=∠C, 试说明∠E=∠F
1
平行线的性质和判定综合应用
还有其它解法吗?
2
3
4
拓展练习
3
证一证
如图,一辆拖拉机经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么?
1420
B
C
A
D
?
解:
∵AB∥CD (已知),
∴∠B=∠C
(两直线平行,内错角相等).
又∵∠B=142° (已知),
∴∠B=∠C=142°
(等量代换).
拓展练习
4
实践应用
一、平行线的性质:
两直线平行
同旁内角互补
内错角相等
同位角相等
已知角之间的关系(相等或互补),得到两直线平行的结论,是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)的结论,是平行线的性质。
课堂小结
二、平行线的性质与判定的区别:
沪科版数学七年级下册
10.3 平行线的性质
第一课时
学习目标
2
3
1
掌握平行线的性质定理,理解它们的图形语言、文字语言、符号语言以及它们之间的转换
会用平行线的性质进行简单的计算和说理,体会几何中图形之间的“位置关系”与“数量关系”有内在 联系
经历探索平行线的性质的过程,让学生树立科学态度,学习探究方法
知识回顾
b
1
2
a
c
c
平行线的判定
两直线平行
同位角相等
内错角相等
同旁内角互补
由“角”定“线”
同位角相等
两直线平行
新知探究
如图: 如果a//b,∠1和∠2相等吗?
b
1
2
a
c
A
C
E
做一做
练习本上的横线都是互相平行的,从中任选两条分别记为AB、CD,画一条直线EF分别与AB、CD相交
B
D
F
任选一组同位角∠1与∠2,量一量他们的度数,有什么发现?
1
2
∠1=∠2
如果两直线不平行,上述结论还成立吗?
两直线不平行,同位角不相等
两直线平行,同位角相等.
平行线的性质1
两条平行线被第三条直线所截,同位角相等.
∴∠1=∠2.
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
新知讲解
如图:已知a//b,那么 2与 3相等吗?为什么
∵a∥b(已知),
∴∠1=∠2
(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
合作探究
解:
两直线平行,内错角相等.
平行线的性质2
两条平行线被第三条直线所截,内错角相等.
∴∠2=∠3.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
3
新知讲解
解: ∵a//b (已知)
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
∴ 1= 2(两直线平行,同位角相等)
∵ 1+ 4=180°(邻补角定义)
∴ 2+ 4=180°(等量代换).
合作探究
你能用一句话表述这个现象吗?
两直线平行,同旁内角互补.
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
∴ 2+ 4=180°.
∵a∥b,
符号语言:
简写为:
b
1
2
a
c
4
新知讲解
整理归纳
平行线的性质
b
1
2
a
c
4
性质1:两直线平行,同位角相等.
∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
性质2:两直线平行,内错角相等.
∵ a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补.
∵ a∥b( 已知 )
∴ ∠1+∠4=180° (两直线平行,同旁内角互补)
两直线平行
同旁内角互补
先知道线的位置关系
后知道角的大小关系
同位角相等
内错角相等
整理归纳
由“线”定“角”
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
判定
判定
判定
性质
性质
性质
整理归纳
平行线的性质与判定的区别
(1)已知∠3 =∠4,∠1=47°,求∠2的度数。
∴∠ 2= ( )
∵ ∠3 =∠4( )
∴a∥ ( )
又∵∠ 1 = 470 ( )
c
1
2
3
4
a
b
d
两直线平行,同位角相等
同位角相等,两直线平行
已知
已知
解:
练一练
完成下列填空
b
470
(2)如图,已知AB∥CD,AC∥BD,∠C= 39°,∠B和∠D是多少度?
1
A
C
B
D
E
解:
练一练
完成下列填空
∵AB∥CD( )
∴∠1=∠ = ° .
( )
C
∵ AC∥BD ,
∴∠B=∠ = °
( )
1
∴∠C+∠ =180°
( )
∴∠D= .
已知
39
两直线平行,同位角相等
39
两直线平行,内错角相等
D
两直线平行,同旁内角互补
141
例1、如图,DA⊥CE于点A,CD∥AB,∠1=30°,求∠D的度数
典例示范
A
C
B
D
E
┓
1
∵DA⊥CE(已知)
∴∠DAE=90°(垂直定义)
∵∠EAB=30°(已知)
∴∠BAD=60°
∵AB∥CD(已知)
∴∠D=∠BAD=60°
(两直线平行。内错角相等)
解:
例3、如图,∠B=80°, ∠CAF =50°,AC平分∠BAF, ,求∠C的度数
A
C
B
F
E
80°
典例示范
解:
∴EF∥BC
(同旁内角互补,两直线平行)
∵AC平分∠BAF( 已知)
∴∠BAF=2 ∠CAF (角平分线定义)
∵∠CAF =50°(已知)
∴∠BAF=2×50°=100°
∵∠B=80°(已知)
∴∠BAF+∠B=100°+80°=180°
∴∠C=∠CAF=50°
(两直线平行,内错角相等)
课堂练习
1、如图,直线AB∥CD,则下列结论正确的是( )
A.∠1=∠2 B.∠3=∠4
C.∠1+∠3=180° D.∠3+∠4=180°
D
1
2
3
4
A
B
C
B
1
选一选
课堂练习
1
选一选
2、如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )
A
C
B
D
┓
B
A.40° B.50° C.60° D.70°
课堂练习
1
选一选
3、如图,直线a∥b,直线c分别与a,b相交于A,B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
A
C
B
a
b
c
2
1
A.38° B.42°
C.48° D.58°
C
课堂练习
2
填一填
1、如图,已知AB//CD,AD//BC.填空:
(1)∵ AB//CD (已知),
∴ ∠1= ∠ ;
( );
(2) ∵ AD//BC (已知)
∴ ∠2= ∠___ 。
( ).
1
A
C
B
D
2
两直线平行,内错角相等.
两直线平行,内错角相等.
D
ACB
A
D
C
B
1、已知,如图,AB∥CD,∠B=∠D,求证:AD∥BC.
证明:
∵AB∥DC(已知)
∴∠B+∠C=180°
(两直线平行,同旁内角互补)
∵∠B=∠D(已知)
∴∠D+∠C=180°(等量代换)
∴AD∥BC(同旁内角互补,两直线平行)
拓展练习
3
证一证
解:∵AB//CD (已知)
∴∠C=∠1 ( )
又∵∠A=∠C(已知)
∴∠A= ( )
∴AE//FC
( )
∴∠E=∠F( )
A
D
E
C
B
F
两直线平行,同位角相等
∠1
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
2、如图,已知AB//CD,∠A=∠C, 试说明∠E=∠F
1
平行线的性质和判定综合应用
还有其它解法吗?
2
3
4
拓展练习
3
证一证
如图,一辆拖拉机经过一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么?
1420
B
C
A
D
?
解:
∵AB∥CD (已知),
∴∠B=∠C
(两直线平行,内错角相等).
又∵∠B=142° (已知),
∴∠B=∠C=142°
(等量代换).
拓展练习
4
实践应用
一、平行线的性质:
两直线平行
同旁内角互补
内错角相等
同位角相等
已知角之间的关系(相等或互补),得到两直线平行的结论,是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)的结论,是平行线的性质。
课堂小结
二、平行线的性质与判定的区别:
