人教版八年级数学下册19.2.2一次函数(图象和性质)与系数关系常见题型 课件(共24张PPT)
文档属性
| 名称 | 人教版八年级数学下册19.2.2一次函数(图象和性质)与系数关系常见题型 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 384.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
19.2 一次函数
第十九章 一次函数
19.2.2 一次函数
第4课时
一次函数图象和性质与系数关系的应用
1
题型
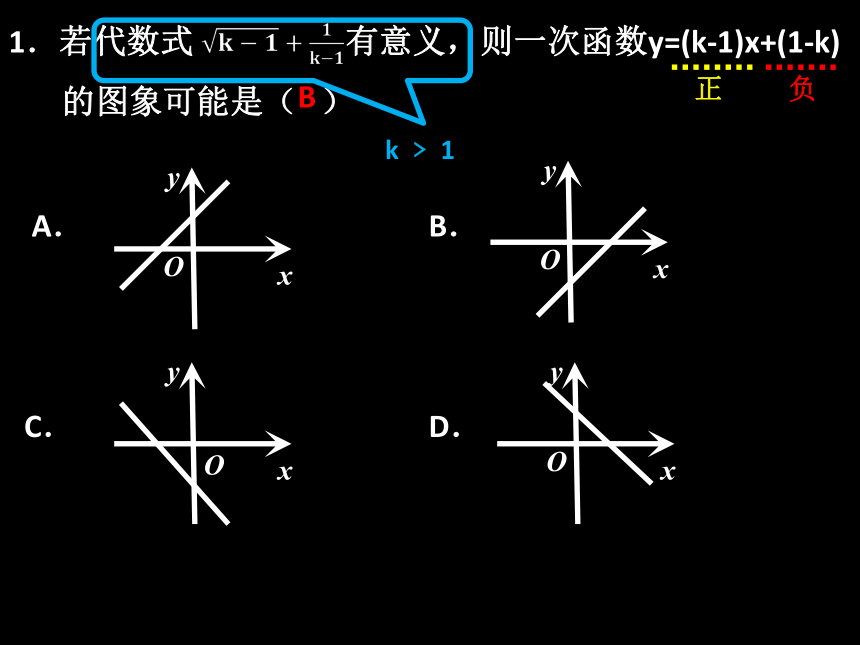
1.若代数式 有意义,则一次函数y=(k-1)x+(1-k)
的图象可能是( )
A. B.
C. D.
O
x
y
O
x
y
O
x
y
O
x
y
k ﹥ 1
正
负
B
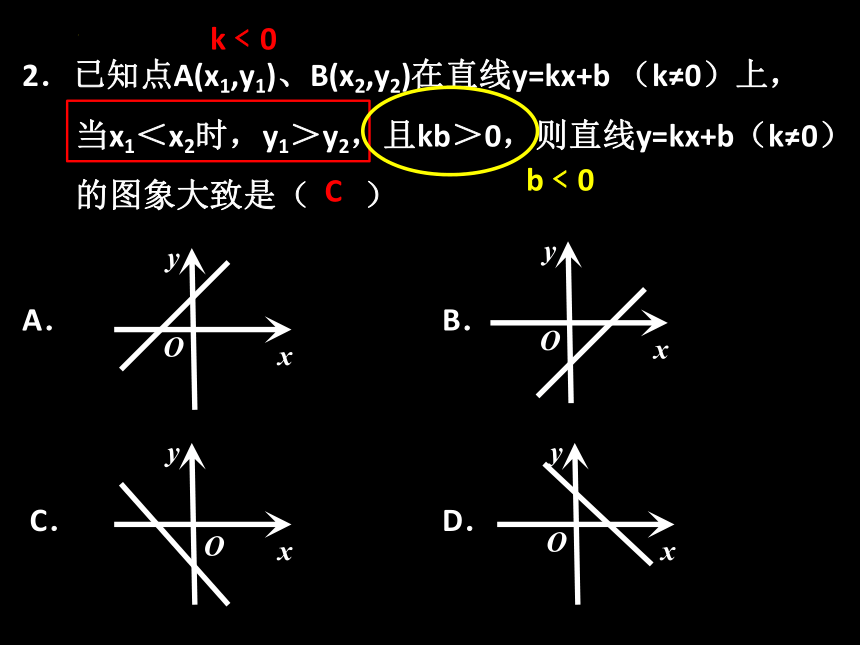
2.已知点A(x1,y1)、B(x2,y2)在直线y=kx+b (k≠0)上,
当x1<x2时,y1>y2,且kb>0,则直线y=kx+b(k≠0)
的图象大致是( )
A. B.
C. D.
C
O
x
y
O
x
y
O
x
y
O
x
y
k﹤0
b﹤0
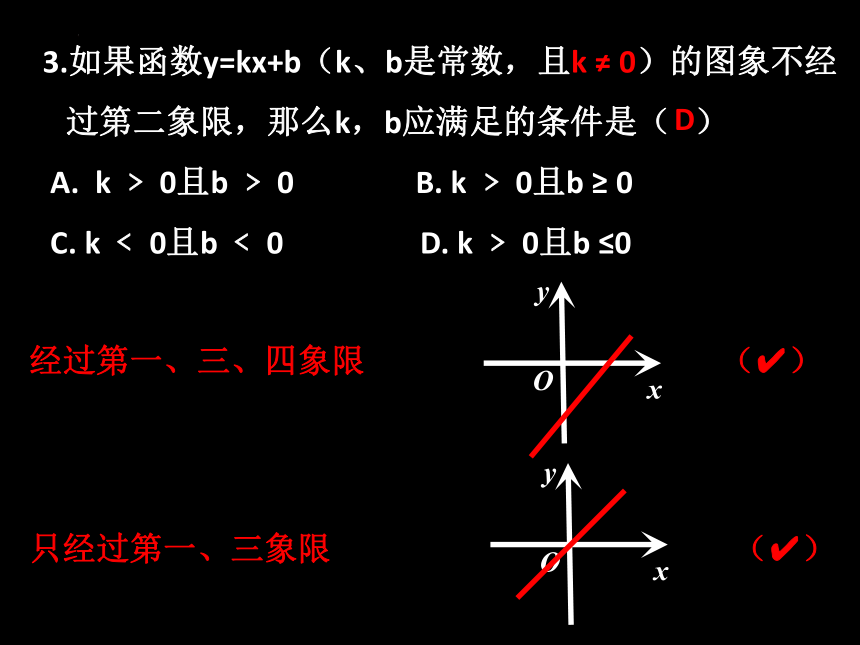
3.如果函数y=kx+b(k、b是常数,且k ≠ 0)的图象不经
过第二象限,那么k,b应满足的条件是( )
A. k ﹥ 0且b ﹥ 0 B. k ﹥ 0且b ≥ 0
C. k ﹤ 0且b ﹤ 0 D. k ﹥ 0且b ≤0
O
x
y
O
x
y
( )
经过第一、三、四象限
只经过第一、三象限
( )
D
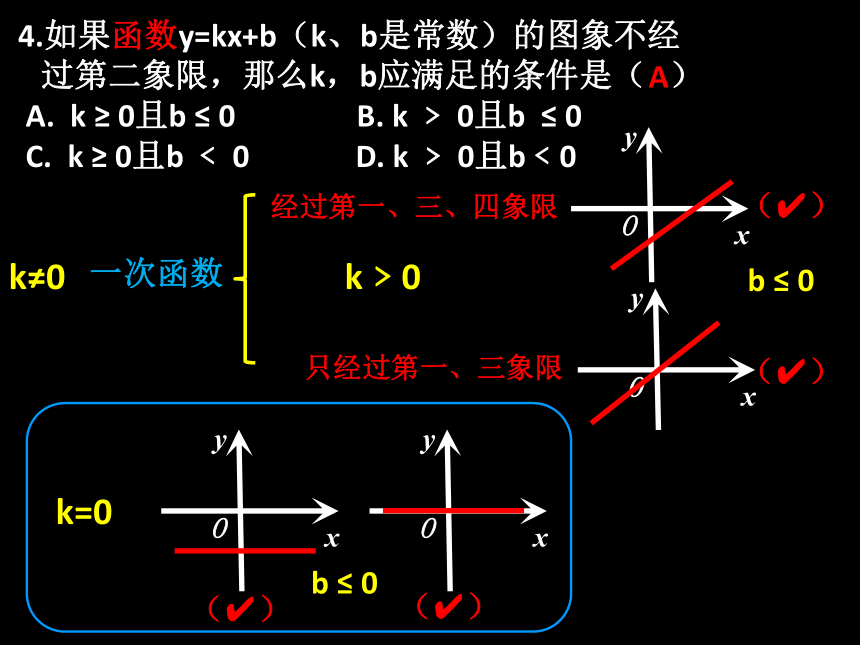
4.如果函数y=kx+b(k、b是常数)的图象不经
过第二象限,那么k,b应满足的条件是( )
A. k ≥ 0且b ≤ 0 B. k ﹥ 0且b ≤ 0
C. k ≥ 0且b ﹤ 0 D. k ﹥ 0且b﹤0
O
x
y
O
x
y
( )
经过第一、三、四象限
只经过第一、三象限
( )
A
O
x
y
k≠0
k=0
O
x
y
( )
( )
b ≤ 0
b ≤ 0
一次函数
k﹥0
5. 在平面直角坐标系中,若直线y=kx+b经过第一、三、
四象限,则直线y=bx+k不经过的象限是 .
∵直线y=kx+b经过第一、三、四象限,
∴k ﹥ 0,b ﹤ 0.
∴直线y=bx+k的图象是
O
x
y
第三象限
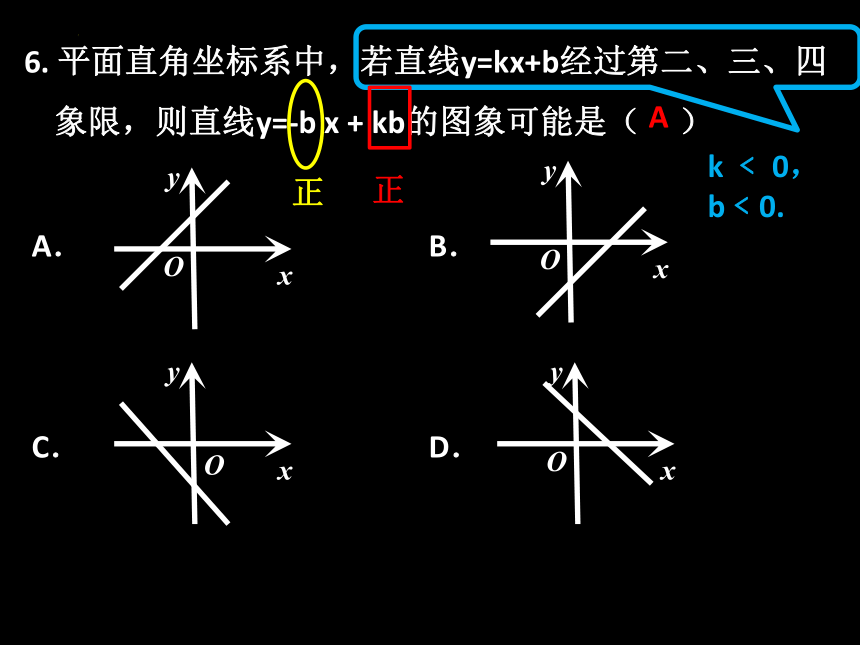
6. 平面直角坐标系中,若直线y=kx+b经过第二、三、四
象限,则直线y=-b x + kb的图象可能是( )
A. B.
C. D.
O
x
y
O
x
y
O
x
y
O
x
y
k ﹤ 0,
b﹤0.
正
正
A
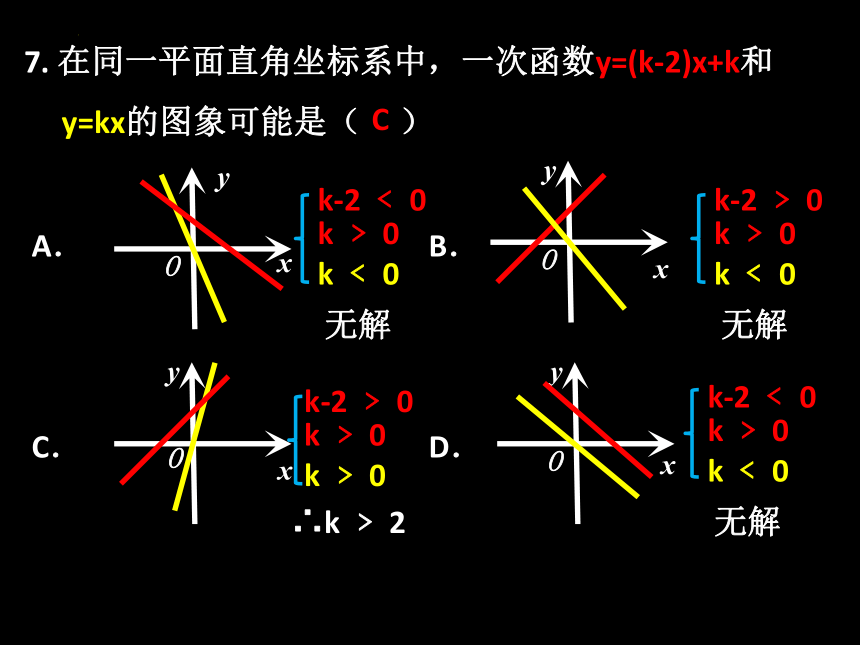
7. 在同一平面直角坐标系中,一次函数y=(k-2)x+k和
y=kx的图象可能是( )
A. B.
C. D.
O
x
y
O
x
y
O
x
y
O
x
y
C
k-2 ﹤ 0
k ﹥ 0
k ﹤ 0
无解
k-2 ﹥ 0
k ﹥ 0
k ﹤ 0
无解
k-2 ﹥ 0
k ﹥ 0
k ﹥ 0
∴k ﹥ 2
k-2 ﹤ 0
k ﹥ 0
k ﹤ 0
无解
8.对于函数y=-2x-1,下列结论正确的是( )
A.它的图象必经过点(-1,0)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大
C
O
x
y
y=-2x-1
x=1
(1,-3)
y=-3
1
1
9.已知一次函数y=(m+3)x+m+5,y随x的增大而减小,
且其图象与y轴的交点在y轴的正半轴上,则m的取值
范围是( )
A.m>-5 B.m<-3 C.-5<m<-3 D.m>-3
C
m+3 ﹤ 0,
由题意得
解得
m +5﹤0,
-5﹤k ﹤-3
10.若点P(a,b)在直线y=2x-1上,则代数式8-4a+2b
的值为______.
6
∵点P(a,b)在直线y=2x-1上,
解:
∴b=2a-1,
变形得:2a-b=1,
代数式8-4a+2b=8 - 2(2a-b)= 8 - 2 × 1 = 6;
11.一次函数y=kx-2的图象经过第二、三、四象限,且
与两坐标轴围成的三角形的面积等于4,则k的值等
于______.
O
x
y
解:
其图象与x轴交于点
与y轴交于点
解得k=0.5或-0.5.
( ,0),
(0,-2),
根据题意可知k﹤0,
∴k=-0.5.
-0.5
12.一次函数y=(a-2)x+1的图象不经过第三象限,化简
.
∵一次函数y=(a-2)x+1的图象不经过第三象限,
解:
∴a-2 ﹤0,
解得a﹤2.
5-2a
一次函数图象和性质在作图中的应用
2
题型
已知一次函数y=(3-m)x+m-4的图象不经过第一象限
且m为整数.
(1)求m的值;
3-m ﹤ 0,
解:由题意得
解得
m -4 ≤0,
3﹤m ≤4.
O
x
y
二
三
四
∵ m为整数,
∴ m=4.
(2)在给定的平面直角坐标系中画出该函数的图象;
O
x
y
1
1
(2)∵ m=4,
∴ y=-x.
①列表:
x
y
0
0
1
-1
y=-x
②描点;
③连线.
(3)当-3 ﹤x ≤ 1时,根据图象求出y的取值范围.
-3
3
-1
(3)-1≤y﹤ 3
素养提升
如图,直线l的解析式为 ,它与坐标轴
分别交于A,B两点.
(1)求点A、B的坐标;
O
x
y
l
A
B
解:(1)
∵令y=0,得x=3;令x=0,得y=4;
∴ A(3,0),B(0,4).
(2)求线段AB的长;
(2)由(1)可知OA=3,OB=4.
∵ ∠AOB=90°,
(3)y轴上是否存在一点C,使得△ABC为等腰三角形?
如果存在,请求出点C的坐标.
(3)存在.
①当点A为等腰三角形顶角的顶点时,
以点A为圆心,AB长为半径画圆,
与y轴交点即为点C.(AB为腰)
C
∵ AB=AC,AO ⊥ BC,
∴ OC=OB=4,
∴ C(0,-4).
追问:
如果点C从y轴上的点(0,12)出发,以每秒1个单位长度的速度
向y轴负半轴运动,求出点C的运动时间.
t=[ 12-(-4) ] ÷1 =16(秒).
O
x
y
l
A
B
3
4
5
变式:
如果点C在x轴上呢?
C
(-2,0)
C
或(8,0)
②当点B为等腰三角形顶角的顶点时,
以点B为圆心,AB长为半径画圆,
与y轴交点即为点C. (AB为腰)
C
∵ BC=BA=5,
∴ C(0,9)或C(0,-1).
追问:
如果点C从y轴上的点(0,12)出发,以每秒1个单位长度的速度
向y轴负半轴运动,求出点C的运动时间.
t=(12-9)÷1 =3(秒).
O
x
y
l
A
B
3
4
5
变式:
如果点C在x轴上呢?
C
(-3,0)
C
或 t=[ 12-(-1) ] ÷1 =13(秒).
③当点C为等腰三角形顶角的顶点时,
作线段AB的垂直平分线,与y轴交点即为点C. (AB为底)
C
设 OC=a,则CA=CB=4-a,
追问:
如果点C从y轴上的点(0,12)出发,以每秒1个单位长度的速度
向y轴负半轴运动,求出点C的运动时间.
O
x
y
l
A
B
3
4
5
变式:
如果点C在x轴上呢?
C
由勾股定理得
∴ C(0, ).
t=(12- )÷1 = (秒).
( ,0)
K﹥0,b﹥0.
O
x
y
y=k x + b
以数释形
数形结合 思想开花
以形析数
课堂小结
19.2 一次函数
第十九章 一次函数
19.2.2 一次函数
第4课时
一次函数图象和性质与系数关系的应用
1
题型
1.若代数式 有意义,则一次函数y=(k-1)x+(1-k)
的图象可能是( )
A. B.
C. D.
O
x
y
O
x
y
O
x
y
O
x
y
k ﹥ 1
正
负
B
2.已知点A(x1,y1)、B(x2,y2)在直线y=kx+b (k≠0)上,
当x1<x2时,y1>y2,且kb>0,则直线y=kx+b(k≠0)
的图象大致是( )
A. B.
C. D.
C
O
x
y
O
x
y
O
x
y
O
x
y
k﹤0
b﹤0
3.如果函数y=kx+b(k、b是常数,且k ≠ 0)的图象不经
过第二象限,那么k,b应满足的条件是( )
A. k ﹥ 0且b ﹥ 0 B. k ﹥ 0且b ≥ 0
C. k ﹤ 0且b ﹤ 0 D. k ﹥ 0且b ≤0
O
x
y
O
x
y
( )
经过第一、三、四象限
只经过第一、三象限
( )
D
4.如果函数y=kx+b(k、b是常数)的图象不经
过第二象限,那么k,b应满足的条件是( )
A. k ≥ 0且b ≤ 0 B. k ﹥ 0且b ≤ 0
C. k ≥ 0且b ﹤ 0 D. k ﹥ 0且b﹤0
O
x
y
O
x
y
( )
经过第一、三、四象限
只经过第一、三象限
( )
A
O
x
y
k≠0
k=0
O
x
y
( )
( )
b ≤ 0
b ≤ 0
一次函数
k﹥0
5. 在平面直角坐标系中,若直线y=kx+b经过第一、三、
四象限,则直线y=bx+k不经过的象限是 .
∵直线y=kx+b经过第一、三、四象限,
∴k ﹥ 0,b ﹤ 0.
∴直线y=bx+k的图象是
O
x
y
第三象限
6. 平面直角坐标系中,若直线y=kx+b经过第二、三、四
象限,则直线y=-b x + kb的图象可能是( )
A. B.
C. D.
O
x
y
O
x
y
O
x
y
O
x
y
k ﹤ 0,
b﹤0.
正
正
A
7. 在同一平面直角坐标系中,一次函数y=(k-2)x+k和
y=kx的图象可能是( )
A. B.
C. D.
O
x
y
O
x
y
O
x
y
O
x
y
C
k-2 ﹤ 0
k ﹥ 0
k ﹤ 0
无解
k-2 ﹥ 0
k ﹥ 0
k ﹤ 0
无解
k-2 ﹥ 0
k ﹥ 0
k ﹥ 0
∴k ﹥ 2
k-2 ﹤ 0
k ﹥ 0
k ﹤ 0
无解
8.对于函数y=-2x-1,下列结论正确的是( )
A.它的图象必经过点(-1,0)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大
C
O
x
y
y=-2x-1
x=1
(1,-3)
y=-3
1
1
9.已知一次函数y=(m+3)x+m+5,y随x的增大而减小,
且其图象与y轴的交点在y轴的正半轴上,则m的取值
范围是( )
A.m>-5 B.m<-3 C.-5<m<-3 D.m>-3
C
m+3 ﹤ 0,
由题意得
解得
m +5﹤0,
-5﹤k ﹤-3
10.若点P(a,b)在直线y=2x-1上,则代数式8-4a+2b
的值为______.
6
∵点P(a,b)在直线y=2x-1上,
解:
∴b=2a-1,
变形得:2a-b=1,
代数式8-4a+2b=8 - 2(2a-b)= 8 - 2 × 1 = 6;
11.一次函数y=kx-2的图象经过第二、三、四象限,且
与两坐标轴围成的三角形的面积等于4,则k的值等
于______.
O
x
y
解:
其图象与x轴交于点
与y轴交于点
解得k=0.5或-0.5.
( ,0),
(0,-2),
根据题意可知k﹤0,
∴k=-0.5.
-0.5
12.一次函数y=(a-2)x+1的图象不经过第三象限,化简
.
∵一次函数y=(a-2)x+1的图象不经过第三象限,
解:
∴a-2 ﹤0,
解得a﹤2.
5-2a
一次函数图象和性质在作图中的应用
2
题型
已知一次函数y=(3-m)x+m-4的图象不经过第一象限
且m为整数.
(1)求m的值;
3-m ﹤ 0,
解:由题意得
解得
m -4 ≤0,
3﹤m ≤4.
O
x
y
二
三
四
∵ m为整数,
∴ m=4.
(2)在给定的平面直角坐标系中画出该函数的图象;
O
x
y
1
1
(2)∵ m=4,
∴ y=-x.
①列表:
x
y
0
0
1
-1
y=-x
②描点;
③连线.
(3)当-3 ﹤x ≤ 1时,根据图象求出y的取值范围.
-3
3
-1
(3)-1≤y﹤ 3
素养提升
如图,直线l的解析式为 ,它与坐标轴
分别交于A,B两点.
(1)求点A、B的坐标;
O
x
y
l
A
B
解:(1)
∵令y=0,得x=3;令x=0,得y=4;
∴ A(3,0),B(0,4).
(2)求线段AB的长;
(2)由(1)可知OA=3,OB=4.
∵ ∠AOB=90°,
(3)y轴上是否存在一点C,使得△ABC为等腰三角形?
如果存在,请求出点C的坐标.
(3)存在.
①当点A为等腰三角形顶角的顶点时,
以点A为圆心,AB长为半径画圆,
与y轴交点即为点C.(AB为腰)
C
∵ AB=AC,AO ⊥ BC,
∴ OC=OB=4,
∴ C(0,-4).
追问:
如果点C从y轴上的点(0,12)出发,以每秒1个单位长度的速度
向y轴负半轴运动,求出点C的运动时间.
t=[ 12-(-4) ] ÷1 =16(秒).
O
x
y
l
A
B
3
4
5
变式:
如果点C在x轴上呢?
C
(-2,0)
C
或(8,0)
②当点B为等腰三角形顶角的顶点时,
以点B为圆心,AB长为半径画圆,
与y轴交点即为点C. (AB为腰)
C
∵ BC=BA=5,
∴ C(0,9)或C(0,-1).
追问:
如果点C从y轴上的点(0,12)出发,以每秒1个单位长度的速度
向y轴负半轴运动,求出点C的运动时间.
t=(12-9)÷1 =3(秒).
O
x
y
l
A
B
3
4
5
变式:
如果点C在x轴上呢?
C
(-3,0)
C
或 t=[ 12-(-1) ] ÷1 =13(秒).
③当点C为等腰三角形顶角的顶点时,
作线段AB的垂直平分线,与y轴交点即为点C. (AB为底)
C
设 OC=a,则CA=CB=4-a,
追问:
如果点C从y轴上的点(0,12)出发,以每秒1个单位长度的速度
向y轴负半轴运动,求出点C的运动时间.
O
x
y
l
A
B
3
4
5
变式:
如果点C在x轴上呢?
C
由勾股定理得
∴ C(0, ).
t=(12- )÷1 = (秒).
( ,0)
K﹥0,b﹥0.
O
x
y
y=k x + b
以数释形
数形结合 思想开花
以形析数
课堂小结
