人教版数学八年级下册 19.2.3一次函数与一元一次方程、不等式 课件(共29张PPT)
文档属性
| 名称 | 人教版数学八年级下册 19.2.3一次函数与一元一次方程、不等式 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 303.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 09:19:36 | ||
图片预览




文档简介
(共29张PPT)
19.2 一次函数
第十九章 一次函数
19.2.3 一次函数与方程、不等式
第1课时
一次函数与一元一次方程、一元一次不等式
导入新课
问题与情境
小明的爸爸应邀来到长春投资,在工业园区投资310万元成本建成一个小型家电生产工厂.建成投产后,为鼓励微型企业,财政直接给补贴10万元.经营一段时
间后,发现不考虑材料费等其它因素,每年盈利75万
元.你能否利用函数图象解答下面两个问题?
(1)该工厂投产几年刚好收回成本?
(2)该工厂从哪一年后回报资金在310万元以上?
讲授新课
一、一次函数与一元一次方程
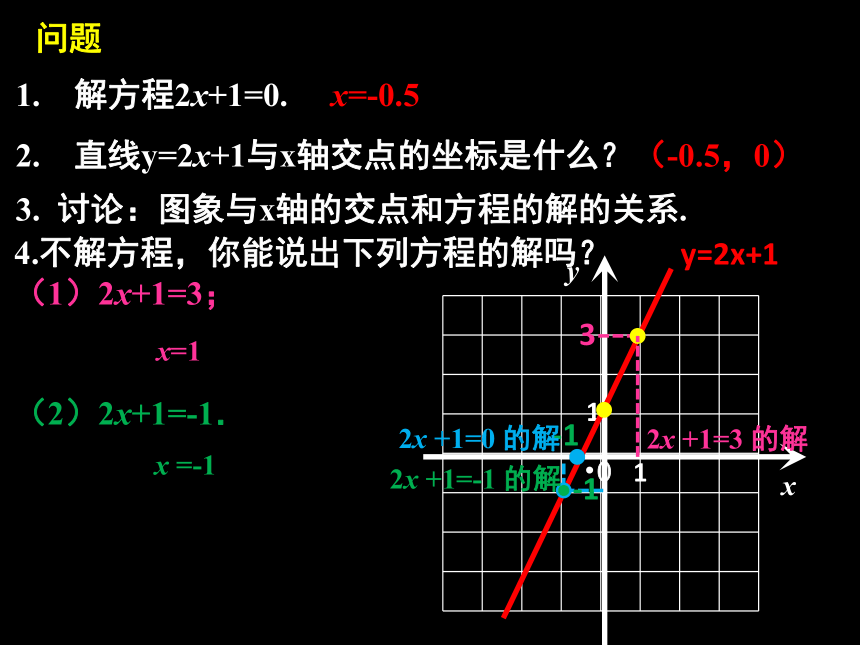
1. 解方程2x+1=0.
O
x
y
1
1
y=2x+1
-1
3
-1
2x +1=3 的解
2x +1=0 的解
2x +1=-1 的解
问题
4.不解方程,你能说出下列方程的解吗?
(1)2x+1=3;
(2)2x+1=-1.
x=-0.5
2. 直线y=2x+1与x轴交点的坐标是什么?
(-0.5,0)
3. 讨论:图象与x轴的交点和方程的解的关系.
x=1
x =-1
知识点总结
知识点1 一次函数与一元一次方程
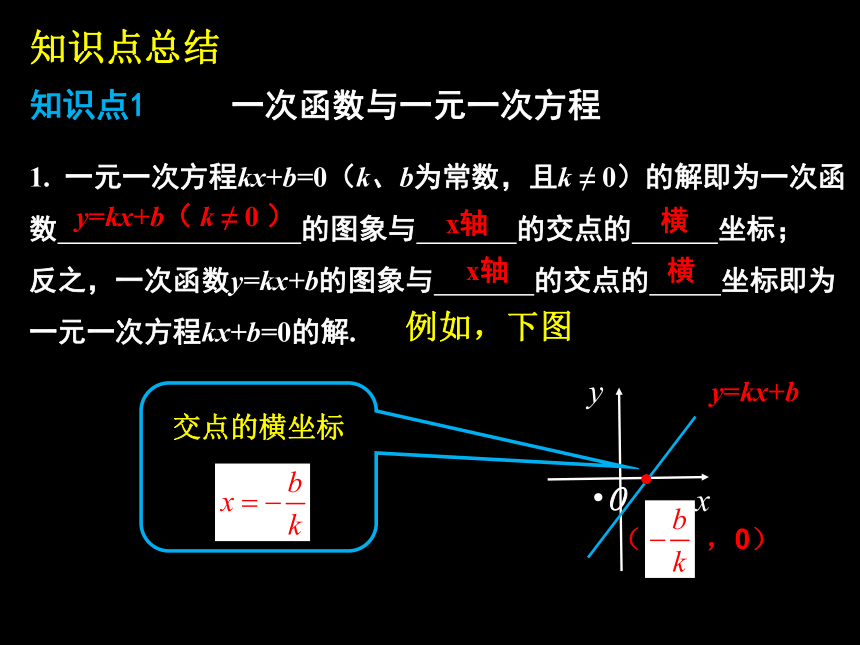
1. 一元一次方程kx+b=0(k、b为常数,且k ≠ 0)的解即为一次函数 的图象与 的交点的 坐标;
反之,一次函数y=kx+b的图象与 的交点的 坐标即为一元一次方程kx+b=0的解.
y=kx+b( k ≠ 0 )
x轴
横
x轴
横
y
x
O
y=kx+b
交点的横坐标
( ,0)
例如,下图
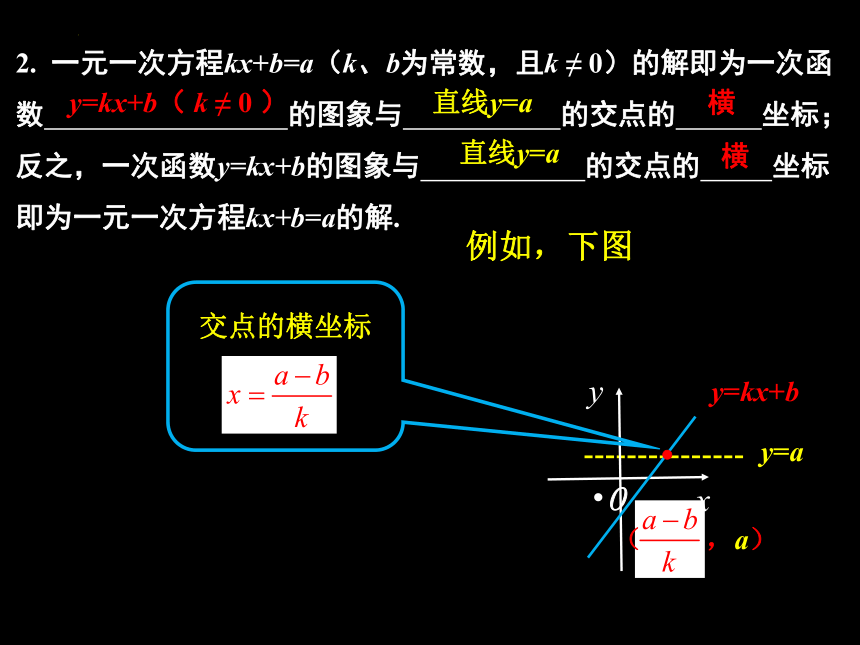
2. 一元一次方程kx+b=a(k、b为常数,且k ≠ 0)的解即为一次函数 的图象与 的交点的 坐标;
反之,一次函数y=kx+b的图象与 的交点的 坐标即为一元一次方程kx+b=a的解.
y=kx+b( k ≠ 0 )
直线y=a
横
直线y=a
横
y
x
O
y=kx+b
交点的横坐标
( ,a)
y=a
例如,下图
范例讲解
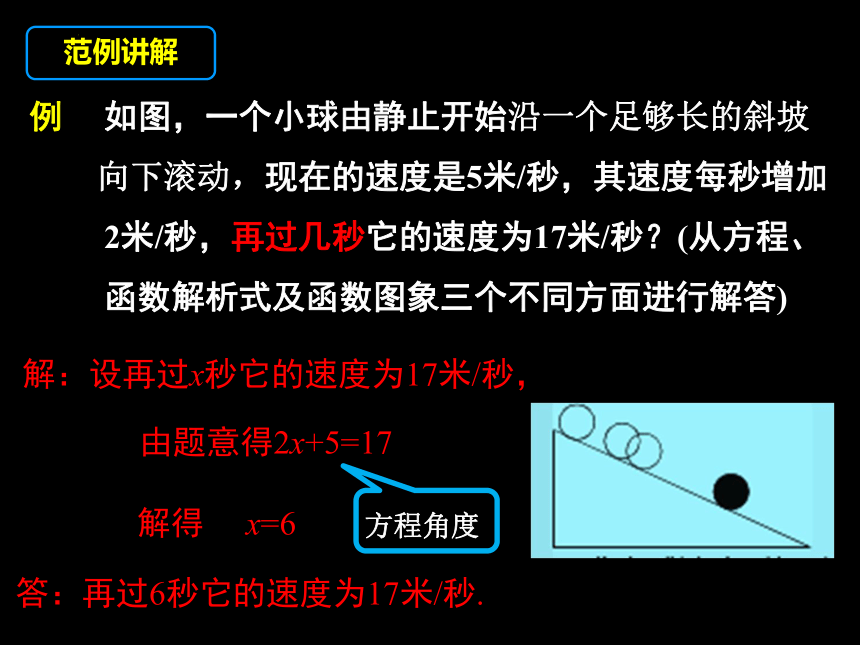
例 如图,一个小球由静止开始沿一个足够长的斜坡
向下滚动,现在的速度是5米/秒,其速度每秒增加
2米/秒,再过几秒它的速度为17米/秒?(从方程、
函数解析式及函数图象三个不同方面进行解答)
解:设再过x秒它的速度为17米/秒,
由题意得2x+5=17
解得 x=6
答:再过6秒它的速度为17米/秒.
方程角度
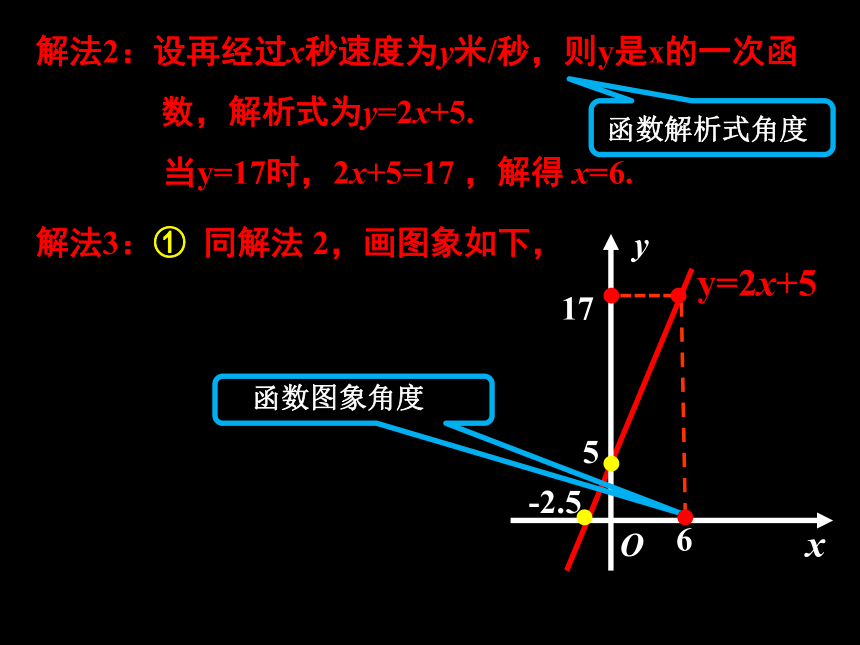
解法2:设再经过x秒速度为y米/秒,则y是x的一次函
数,解析式为y=2x+5.
当y=17时,2x+5=17 ,解得 x=6.
函数解析式角度
解法3:① 同解法 2,画图象如下,
y=2x+5
x
y
O
6
17
5
-2.5
函数图象角度
解法3:② 同解法1得2x+5=17,化简得2x-12=0.
设y=2x-12,画图象如下,
y=2x-12
x
y
O
6
-12
函数图象角度
小试牛刀
1.观察图(1):-x-2=0的解为 ;
O
x
y
-2
-2
y=-x-2
图(1)
O
x
y
1
-1
y=x-1
图(2)
观察图(2): x-1=0的解为 .
x=-2
y=0
y=0
x=1
O
x
y
3
-3
y=ax+b
2题图
2. 已知函数y=ax+b的图象如图所示,则方程ax+b=0的
解为 ;
y=0
x=3
3. 若函数y=3x-b的图象如图所示,则方程3x-b=0的解与b的值
分别为( )
A. x=-1 , b=3 B. x=-1 , b=-3
C. x=1 , b=3 D. x=1 , b=-3
O
x
y
1
y=3x-b
3题图
y=0
x=1
C
素养提升
y=kx+b
如图,根据函数y=kx+b (k、b为常数,且k ≠ 0)的图象,求
(1)方程kx+b =0的解;
解:(1)一次函数y=kx+b的图象与x轴的交点的横坐标就是一
元一次方程kx+b=0的解,即x=2.
(2)式子k+b 的值;
(2)一次函数y=kx+b的自变量x=1
时对应的y值就是式子k+b 的值,
即式子k+b 的值为-1.
O
x
y
1
1
2
3
4
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
y=kx+b
O
x
y
1
1
2
3
4
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
(3)式子k-b的值.
(3)一次函数y=kx+b的自变量x=-1时对应的y值
就是式子-k+b 的值,即式子-k+b 的值为-3.
∴ k-b=3.
二、一次函数与一元一次不等式
问题
O
x
y
1
1
y=2x+1
y﹥0
不等式2x+1﹥ 0的解集就是
使函数y=2x+1的函数值大于0,
即x轴上方的函数图象对应的
自变量取值范围;
1. 继续观察一次函数y=2x+1的图象.
2. 如何从图象上找出不等式2x+1﹥0的解集.
x﹥-0.5
(-0.5,0)
O
x
y
1
1
y=2x+1
不等式2x+1 ﹤ 0的解集就是使函数y=2x+1的函数值小于0,即x轴下方的函数图象对应的自变量取值范围;
3. 如何从图象上找出不等式2x+1 ﹤ 0的解集.
y﹤0
x﹤-0.5
(-0.5,0)
4. 通过上面两个问题的思考,你能发现一次函数y=kx+b
(k、b为常数,且k ≠ 0)与
一元一次不等式kx+b﹥0或kx+b ﹤ 0 (k、b为常数,且k ≠ 0)的关系吗?
5.不解不等式 ,利用图象求出-3x+6 ≤ 3的解集;
解:
O
x
y
1
1
y=-3x+6
画函数y=-3x+6的图象.
x 1
y 0
3
2
(2)描点;
(3)连线.
图象如图所示.
由图象可知,不等式 -3x+6 ≤ 3
的解集是函数y=-3x+6图象位于
直线y=3下方部分的点的横坐标
的取值范围,即x ≥ 1;
(1,3)
(1)列表:
6. 通过以上探究,你能总结
一次函数与一元一次不等
式之间的联系吗?
你能求出0≤-3x+6 ≤ 3的解集吗?
1≤x ≤ 2
知识点2 一次函数与一元一次不等式
1. 一元一次不等式kx+b ﹥ 0(或kx+b ﹤ 0)(k、b为常数,且
k ≠ 0) 的解集,就是一次函数 的图象在
x轴 (或 )相应的自变量x的取值范围.
上方
y=kx+b( k ≠ 0 )
下方
y
x
O
y=kx+b
( ,0)
x轴下方
x轴上方
例如,下图
2. 一元一次不等式kx+b ﹥ a(或kx+b ﹤ a)(k、b为常数,且
k ≠ 0) 的解集,就是一次函数 的图象在直线y=a (或 )的点对应的横坐标的取值范围.
上方
y=kx+b( k ≠ 0 )
下方
y
x
O
y=kx+b
直线y=a下方
直线y=a上方
y=a
( ,a)
例如,下图
不解不等式,利用图象解不等式:
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
O
x
y
1
1
y=3x+2
y=2
范例讲解
解:
(1)x>0;
(3)x<-1.
小试牛刀
1.观察图(1):不等式kx+b ﹤ 0的解集为 ;
O
x
y
1
-2
y=kx+b
图(1)
2.观察图(2): ax-1 ﹥2的解集为 .
x ﹤1
y ﹤ 0
y ﹥2
x﹥1
O
x
y
1
2
y=ax-1
图(2)
素养提升
如图,一次函数y=kx+b(k﹥0)的图象过点(-1,0),则
不等式k(x-1)+ b﹥0的解集为( )
A. x﹥-2 B. x﹥-1 C. x﹥0 D. x﹥1
C
O
x
y
1
-1
y=kx+b
2题图
1
y=k(x-1)+ b
变式:
不等式k(x-2)+ b﹥0的解集为( )
D
y=k(x-2)+ b
学以致用
小明的爸爸应邀来到长春投资,在工业园区投资310万元成本建成一个小型家电生产工厂.建成投产后,为鼓励微型企业,财政直接给补贴10万元.经营一段时
间后,发现不考虑材料费等其它因素,每年盈利75万
元.回答下面两个问题.
(1)该工厂投产几年刚好收回成本?
(2)该工厂从哪一年后回报总资金在310万元以上?
解:设小明的爸爸投产时间为x年,获得回报总资金
为 y万元,则y=10+75x(x ≥ 0).
10
4
O
x/年
y/万元
2
3
1
310
y=75x+10 (x ≥ 0)
5
(1)该工厂投产4年刚好收回成本;
(2)该工厂从第4年后回报总资金在310万元以上.
课堂小结
从形到数,从数到形,从形可以知道数的范围,从数可以知道形的特征,我们在这种抽象思维与形象思维转换中体会了数学的无穷乐趣,这就是我们这节课的主题.
放弃很容易,但坚持一定很酷.
人生一次,怎愿甘拜下风,别认输,你有多努力,就有多特殊!
—加油
教师寄语
19.2 一次函数
第十九章 一次函数
19.2.3 一次函数与方程、不等式
第1课时
一次函数与一元一次方程、一元一次不等式
导入新课
问题与情境
小明的爸爸应邀来到长春投资,在工业园区投资310万元成本建成一个小型家电生产工厂.建成投产后,为鼓励微型企业,财政直接给补贴10万元.经营一段时
间后,发现不考虑材料费等其它因素,每年盈利75万
元.你能否利用函数图象解答下面两个问题?
(1)该工厂投产几年刚好收回成本?
(2)该工厂从哪一年后回报资金在310万元以上?
讲授新课
一、一次函数与一元一次方程
1. 解方程2x+1=0.
O
x
y
1
1
y=2x+1
-1
3
-1
2x +1=3 的解
2x +1=0 的解
2x +1=-1 的解
问题
4.不解方程,你能说出下列方程的解吗?
(1)2x+1=3;
(2)2x+1=-1.
x=-0.5
2. 直线y=2x+1与x轴交点的坐标是什么?
(-0.5,0)
3. 讨论:图象与x轴的交点和方程的解的关系.
x=1
x =-1
知识点总结
知识点1 一次函数与一元一次方程
1. 一元一次方程kx+b=0(k、b为常数,且k ≠ 0)的解即为一次函数 的图象与 的交点的 坐标;
反之,一次函数y=kx+b的图象与 的交点的 坐标即为一元一次方程kx+b=0的解.
y=kx+b( k ≠ 0 )
x轴
横
x轴
横
y
x
O
y=kx+b
交点的横坐标
( ,0)
例如,下图
2. 一元一次方程kx+b=a(k、b为常数,且k ≠ 0)的解即为一次函数 的图象与 的交点的 坐标;
反之,一次函数y=kx+b的图象与 的交点的 坐标即为一元一次方程kx+b=a的解.
y=kx+b( k ≠ 0 )
直线y=a
横
直线y=a
横
y
x
O
y=kx+b
交点的横坐标
( ,a)
y=a
例如,下图
范例讲解
例 如图,一个小球由静止开始沿一个足够长的斜坡
向下滚动,现在的速度是5米/秒,其速度每秒增加
2米/秒,再过几秒它的速度为17米/秒?(从方程、
函数解析式及函数图象三个不同方面进行解答)
解:设再过x秒它的速度为17米/秒,
由题意得2x+5=17
解得 x=6
答:再过6秒它的速度为17米/秒.
方程角度
解法2:设再经过x秒速度为y米/秒,则y是x的一次函
数,解析式为y=2x+5.
当y=17时,2x+5=17 ,解得 x=6.
函数解析式角度
解法3:① 同解法 2,画图象如下,
y=2x+5
x
y
O
6
17
5
-2.5
函数图象角度
解法3:② 同解法1得2x+5=17,化简得2x-12=0.
设y=2x-12,画图象如下,
y=2x-12
x
y
O
6
-12
函数图象角度
小试牛刀
1.观察图(1):-x-2=0的解为 ;
O
x
y
-2
-2
y=-x-2
图(1)
O
x
y
1
-1
y=x-1
图(2)
观察图(2): x-1=0的解为 .
x=-2
y=0
y=0
x=1
O
x
y
3
-3
y=ax+b
2题图
2. 已知函数y=ax+b的图象如图所示,则方程ax+b=0的
解为 ;
y=0
x=3
3. 若函数y=3x-b的图象如图所示,则方程3x-b=0的解与b的值
分别为( )
A. x=-1 , b=3 B. x=-1 , b=-3
C. x=1 , b=3 D. x=1 , b=-3
O
x
y
1
y=3x-b
3题图
y=0
x=1
C
素养提升
y=kx+b
如图,根据函数y=kx+b (k、b为常数,且k ≠ 0)的图象,求
(1)方程kx+b =0的解;
解:(1)一次函数y=kx+b的图象与x轴的交点的横坐标就是一
元一次方程kx+b=0的解,即x=2.
(2)式子k+b 的值;
(2)一次函数y=kx+b的自变量x=1
时对应的y值就是式子k+b 的值,
即式子k+b 的值为-1.
O
x
y
1
1
2
3
4
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
y=kx+b
O
x
y
1
1
2
3
4
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
(3)式子k-b的值.
(3)一次函数y=kx+b的自变量x=-1时对应的y值
就是式子-k+b 的值,即式子-k+b 的值为-3.
∴ k-b=3.
二、一次函数与一元一次不等式
问题
O
x
y
1
1
y=2x+1
y﹥0
不等式2x+1﹥ 0的解集就是
使函数y=2x+1的函数值大于0,
即x轴上方的函数图象对应的
自变量取值范围;
1. 继续观察一次函数y=2x+1的图象.
2. 如何从图象上找出不等式2x+1﹥0的解集.
x﹥-0.5
(-0.5,0)
O
x
y
1
1
y=2x+1
不等式2x+1 ﹤ 0的解集就是使函数y=2x+1的函数值小于0,即x轴下方的函数图象对应的自变量取值范围;
3. 如何从图象上找出不等式2x+1 ﹤ 0的解集.
y﹤0
x﹤-0.5
(-0.5,0)
4. 通过上面两个问题的思考,你能发现一次函数y=kx+b
(k、b为常数,且k ≠ 0)与
一元一次不等式kx+b﹥0或kx+b ﹤ 0 (k、b为常数,且k ≠ 0)的关系吗?
5.不解不等式 ,利用图象求出-3x+6 ≤ 3的解集;
解:
O
x
y
1
1
y=-3x+6
画函数y=-3x+6的图象.
x 1
y 0
3
2
(2)描点;
(3)连线.
图象如图所示.
由图象可知,不等式 -3x+6 ≤ 3
的解集是函数y=-3x+6图象位于
直线y=3下方部分的点的横坐标
的取值范围,即x ≥ 1;
(1,3)
(1)列表:
6. 通过以上探究,你能总结
一次函数与一元一次不等
式之间的联系吗?
你能求出0≤-3x+6 ≤ 3的解集吗?
1≤x ≤ 2
知识点2 一次函数与一元一次不等式
1. 一元一次不等式kx+b ﹥ 0(或kx+b ﹤ 0)(k、b为常数,且
k ≠ 0) 的解集,就是一次函数 的图象在
x轴 (或 )相应的自变量x的取值范围.
上方
y=kx+b( k ≠ 0 )
下方
y
x
O
y=kx+b
( ,0)
x轴下方
x轴上方
例如,下图
2. 一元一次不等式kx+b ﹥ a(或kx+b ﹤ a)(k、b为常数,且
k ≠ 0) 的解集,就是一次函数 的图象在直线y=a (或 )的点对应的横坐标的取值范围.
上方
y=kx+b( k ≠ 0 )
下方
y
x
O
y=kx+b
直线y=a下方
直线y=a上方
y=a
( ,a)
例如,下图
不解不等式,利用图象解不等式:
(1)3x+2>2;(2)3x+2<0;(3)3x+2<-1.
O
x
y
1
1
y=3x+2
y=2
范例讲解
解:
(1)x>0;
(3)x<-1.
小试牛刀
1.观察图(1):不等式kx+b ﹤ 0的解集为 ;
O
x
y
1
-2
y=kx+b
图(1)
2.观察图(2): ax-1 ﹥2的解集为 .
x ﹤1
y ﹤ 0
y ﹥2
x﹥1
O
x
y
1
2
y=ax-1
图(2)
素养提升
如图,一次函数y=kx+b(k﹥0)的图象过点(-1,0),则
不等式k(x-1)+ b﹥0的解集为( )
A. x﹥-2 B. x﹥-1 C. x﹥0 D. x﹥1
C
O
x
y
1
-1
y=kx+b
2题图
1
y=k(x-1)+ b
变式:
不等式k(x-2)+ b﹥0的解集为( )
D
y=k(x-2)+ b
学以致用
小明的爸爸应邀来到长春投资,在工业园区投资310万元成本建成一个小型家电生产工厂.建成投产后,为鼓励微型企业,财政直接给补贴10万元.经营一段时
间后,发现不考虑材料费等其它因素,每年盈利75万
元.回答下面两个问题.
(1)该工厂投产几年刚好收回成本?
(2)该工厂从哪一年后回报总资金在310万元以上?
解:设小明的爸爸投产时间为x年,获得回报总资金
为 y万元,则y=10+75x(x ≥ 0).
10
4
O
x/年
y/万元
2
3
1
310
y=75x+10 (x ≥ 0)
5
(1)该工厂投产4年刚好收回成本;
(2)该工厂从第4年后回报总资金在310万元以上.
课堂小结
从形到数,从数到形,从形可以知道数的范围,从数可以知道形的特征,我们在这种抽象思维与形象思维转换中体会了数学的无穷乐趣,这就是我们这节课的主题.
放弃很容易,但坚持一定很酷.
人生一次,怎愿甘拜下风,别认输,你有多努力,就有多特殊!
—加油
教师寄语
