人教版八年级下册20.2 数据的波动程度课件(共27张PPT)
文档属性
| 名称 | 人教版八年级下册20.2 数据的波动程度课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 249.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
20.2.1 数据的波动程度
1.理解方差的概念及统计学意义;
2.会计算一组数据的方差;
3.能够运用方差判断数据的波动程度,并解决简单的实际问题.
学习目标
重点:会计算一组数据的方差.
难点:能够运用方差判断数据的波动程度,并解决简单的实际问题.
重难点
我们学习了数据分析的一些知识. 平均数、中位数、众数是三个不同的代表数,可描述数据的数值的一般水平或集中趋势.
数据的分析要选择恰当的形式,要根据具体情况选用统计表、统计图,或者用平均数、众数、中位数来描述.
在数据分析中还有其他情况出现:如:数据与其平均数的偏离程度. 如何分析数据的稳定性?
知识回顾
课前预习
阅读课本,了解本节主要内容.
刘亮和李飞参加射击训练的成绩(单位:环)如下:
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
若你是教练,你认为挑选哪一位比较适宜?
新课导入
动脑筋
现要挑选一名射击手参加比赛.
(1) 两人的平均成绩分别是多少?
(2) 如何反映这两组数据与其平均数的偏离程度?
(3) 谁的成绩比较稳定?
从哪几个问题考虑?
新知讲解
刘亮成绩的平均数是=8.0
李飞成绩的平均数是=8.0
即两人的平均成绩相同.
新知讲解
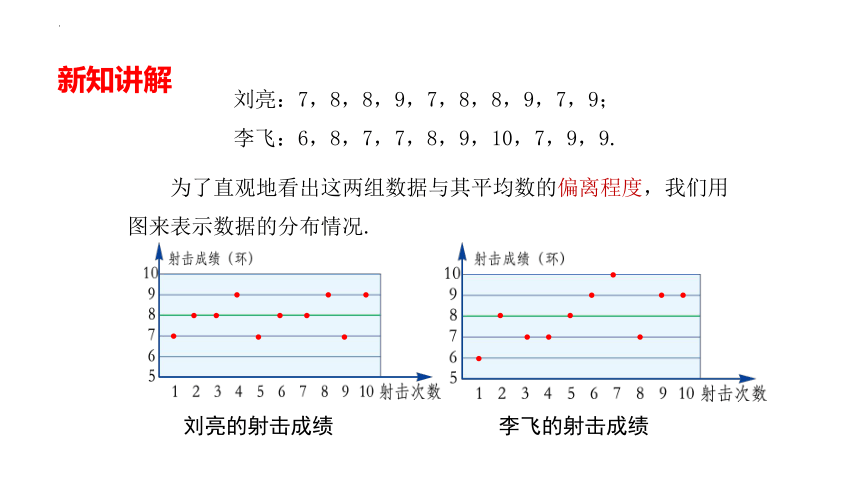
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
为了直观地看出这两组数据与其平均数的偏离程度,我们用图来表示数据的分布情况.
刘亮的射击成绩
李飞的射击成绩
新知讲解
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
由上面两幅图,可以发现刘亮的射击成绩大多集中在平均成绩8环附近,
而李飞的射击成绩与其平均成绩的偏差较大.
刘亮的射击成绩
李飞的射击成绩
新知讲解
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的离散程度或波动大小.
那么如何找到一个特征值来反映一组数据与其平均数的离散程度呢?
新知讲解
1.将各个数与平均数之差相加. 但是相加的结果为0.
2.把各个数与平均数之差取绝对值,再取它们的平均值.
3.把各个数与平均数之差平方,再取它们的平均值.
为了反映一组数据的离散程度,可以采用很多方法,统计中常采用以下做法:
设一组数据为x1,x2,…,xn,各数据与平均数之差的平方的平均值,叫做这组数据的方差,记做s2.
即
新知讲解
由此我们可以算出刘亮、李飞的射击成绩的方差分别是
计算结果表明: s2李飞 > s2刘亮,这说明李飞的射击成绩波动大,而刘亮的射击成绩波动小,因此刘亮的射击成绩稳定.
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
s2刘亮==0.6
s2李飞==1.4
新知讲解
例. 有两个女声小合唱队,各由5名队员组成.她们的身高为(单位:cm)为:
甲队:160,162,159,160,159;
乙队:180,160,150,150,160.
如果单从队员的身高考虑,哪队的演出形象效果好?
例题分析
解: 甲队队员的平均身高是
甲队队员身高的方差是
乙队队员的平均身高是
乙队队员身高的方差是
甲
乙
=1.2
=120
甲队:160,162,159,160,159;
乙队:180,160,150,150,160.
计算的结果表明:
乙队队员身高的方差比甲队队员身高的方差大很多,这说明乙队中各队员的身高波动大,而甲队中各队员的身高波动小,所以甲队队员的身高比较整齐,形象效果好.
从例题的计算过程可以看到,求方差的运算量很大. 当一组数据所含的数很多时,我们可以借助计算器来求一组数据的方差.
不同型号的计算器其操作步骤可能不同,请先阅读计算器的说明书.通常先按统计键,使计算器进入统计运算模式,然后依次输入数据,最后按求方差的功能键,即可求出该组数据的方差.
新知讲解
1.用计算器求下列各组数据的平均数和方差:
(1) 24,24,31,31,47,47,62,84,95,95;
(2)473,284,935,743,586,654;
(3)10.1,9.8,9.7,10.2,10.3,9.9,10.0 .
答:平均数为54,方差为728.2 .
答:平均数为612.5,方差为41805.58 .
答:平均数为10,方差为0.04.
跟踪训练
2. 李明的班上要派一名选手参加学校田径运动会的100m 比赛,李明和张亮都希望自己能参加比赛,他们在训练中10次的测试成绩(单位:s)分别是:
李明:14.5,14.9,14.2,15.0,14.7,14.1,14.4,13.9,15.5,14.8;
张亮:14.8,14.4,15.5,14.1,14.3,14.6,14.1, 14.8,15.1,14.3.
根据两人的成绩,应该派谁去参加比赛?
答:李明的平均成绩为14.6s ,张亮的平均成绩为14.6s.
李明成绩的方差为0.206,张亮成绩的方差为0.186.
由于张亮成绩波动小,所以应该派张亮去参加比赛.
跟踪训练
3. 已知数据a1,a2,a3,…,an的平均数为x,方差为y,则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为________,方差为________.
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为________ ,方差为________.
③数据3a1,3a2 ,3a3 ,…,3an的平均数为________ ,方差为________.
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为________ ,方差为________.
x+3
y
x-3
y
3x
9y
2x-3
4y
跟踪训练
1. (潍坊)甲、乙、丙、丁四名射击运动员在选拔赛中,每人各射击了10次,甲、乙两人的成绩如下表所示,丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数和方差两个因素分析,应选( )
甲 乙
平均数 9 8
方差 1 1
A.甲 B.乙 C.丙 D.丁
C
链接中考
方差s2= ×[(5-7)2+(8-7)2+(7-7)2+(6-7)2+(9-7)2]=2
2. (绥化)在一次射击训练中,某名选手五次射击的环数分别为5,8,7,6,9,则这名选手五次射击环数的方差为________.
2
五次射击的平均成绩为: ×(5+8+7+6+9)=7,
链接中考
2. 一组数据:a,a,a,…,a (有n个a)则它的方差为_____.
1. 有5个数1,4,a,5,2的平均数是a,则这5个数的方差是______.
2
0
3. 已知一组数据的方差是2,如果每个数据都加3得到一组新数据,则新数据的方差是______.
2
随堂检测
4. 已知一组数据的方差是2,如果每个数据都乘3得到一组新数据,则新数据的方差是______.
18
5. 甲、乙两名战士在射击训练中,打靶的次数相同,且射击成绩的平均数也相同,如果甲的射击成绩比较稳定,那么方差的大小关系是:s2甲______s2乙.
<
随堂检测
6. 小明本期五次测验的数学和英语成绩分别如下(单位:分)
数学 70 95 75 95 90
英语 80 85 90 85 85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数:都是85
方差:①数学 115;②英语 10
英语较稳定但要提高;数学不够稳定有待努力进步!
随堂检测
方差
课堂小结
公式:
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
20.2.1 数据的波动程度
1.理解方差的概念及统计学意义;
2.会计算一组数据的方差;
3.能够运用方差判断数据的波动程度,并解决简单的实际问题.
学习目标
重点:会计算一组数据的方差.
难点:能够运用方差判断数据的波动程度,并解决简单的实际问题.
重难点
我们学习了数据分析的一些知识. 平均数、中位数、众数是三个不同的代表数,可描述数据的数值的一般水平或集中趋势.
数据的分析要选择恰当的形式,要根据具体情况选用统计表、统计图,或者用平均数、众数、中位数来描述.
在数据分析中还有其他情况出现:如:数据与其平均数的偏离程度. 如何分析数据的稳定性?
知识回顾
课前预习
阅读课本,了解本节主要内容.
刘亮和李飞参加射击训练的成绩(单位:环)如下:
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
若你是教练,你认为挑选哪一位比较适宜?
新课导入
动脑筋
现要挑选一名射击手参加比赛.
(1) 两人的平均成绩分别是多少?
(2) 如何反映这两组数据与其平均数的偏离程度?
(3) 谁的成绩比较稳定?
从哪几个问题考虑?
新知讲解
刘亮成绩的平均数是=8.0
李飞成绩的平均数是=8.0
即两人的平均成绩相同.
新知讲解
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
为了直观地看出这两组数据与其平均数的偏离程度,我们用图来表示数据的分布情况.
刘亮的射击成绩
李飞的射击成绩
新知讲解
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
由上面两幅图,可以发现刘亮的射击成绩大多集中在平均成绩8环附近,
而李飞的射击成绩与其平均成绩的偏差较大.
刘亮的射击成绩
李飞的射击成绩
新知讲解
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的离散程度或波动大小.
那么如何找到一个特征值来反映一组数据与其平均数的离散程度呢?
新知讲解
1.将各个数与平均数之差相加. 但是相加的结果为0.
2.把各个数与平均数之差取绝对值,再取它们的平均值.
3.把各个数与平均数之差平方,再取它们的平均值.
为了反映一组数据的离散程度,可以采用很多方法,统计中常采用以下做法:
设一组数据为x1,x2,…,xn,各数据与平均数之差的平方的平均值,叫做这组数据的方差,记做s2.
即
新知讲解
由此我们可以算出刘亮、李飞的射击成绩的方差分别是
计算结果表明: s2李飞 > s2刘亮,这说明李飞的射击成绩波动大,而刘亮的射击成绩波动小,因此刘亮的射击成绩稳定.
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
s2刘亮==0.6
s2李飞==1.4
新知讲解
例. 有两个女声小合唱队,各由5名队员组成.她们的身高为(单位:cm)为:
甲队:160,162,159,160,159;
乙队:180,160,150,150,160.
如果单从队员的身高考虑,哪队的演出形象效果好?
例题分析
解: 甲队队员的平均身高是
甲队队员身高的方差是
乙队队员的平均身高是
乙队队员身高的方差是
甲
乙
=1.2
=120
甲队:160,162,159,160,159;
乙队:180,160,150,150,160.
计算的结果表明:
乙队队员身高的方差比甲队队员身高的方差大很多,这说明乙队中各队员的身高波动大,而甲队中各队员的身高波动小,所以甲队队员的身高比较整齐,形象效果好.
从例题的计算过程可以看到,求方差的运算量很大. 当一组数据所含的数很多时,我们可以借助计算器来求一组数据的方差.
不同型号的计算器其操作步骤可能不同,请先阅读计算器的说明书.通常先按统计键,使计算器进入统计运算模式,然后依次输入数据,最后按求方差的功能键,即可求出该组数据的方差.
新知讲解
1.用计算器求下列各组数据的平均数和方差:
(1) 24,24,31,31,47,47,62,84,95,95;
(2)473,284,935,743,586,654;
(3)10.1,9.8,9.7,10.2,10.3,9.9,10.0 .
答:平均数为54,方差为728.2 .
答:平均数为612.5,方差为41805.58 .
答:平均数为10,方差为0.04.
跟踪训练
2. 李明的班上要派一名选手参加学校田径运动会的100m 比赛,李明和张亮都希望自己能参加比赛,他们在训练中10次的测试成绩(单位:s)分别是:
李明:14.5,14.9,14.2,15.0,14.7,14.1,14.4,13.9,15.5,14.8;
张亮:14.8,14.4,15.5,14.1,14.3,14.6,14.1, 14.8,15.1,14.3.
根据两人的成绩,应该派谁去参加比赛?
答:李明的平均成绩为14.6s ,张亮的平均成绩为14.6s.
李明成绩的方差为0.206,张亮成绩的方差为0.186.
由于张亮成绩波动小,所以应该派张亮去参加比赛.
跟踪训练
3. 已知数据a1,a2,a3,…,an的平均数为x,方差为y,则
①数据a1+3,a2 + 3,a3 +3 ,…,an +3的平均数为________,方差为________.
②数据a1-3,a2 -3,a3 -3 ,…,an -3的平均数为________ ,方差为________.
③数据3a1,3a2 ,3a3 ,…,3an的平均数为________ ,方差为________.
④数据2a1-3,2a2 -3,2a3 -3 ,…,2an -3的平均数为________ ,方差为________.
x+3
y
x-3
y
3x
9y
2x-3
4y
跟踪训练
1. (潍坊)甲、乙、丙、丁四名射击运动员在选拔赛中,每人各射击了10次,甲、乙两人的成绩如下表所示,丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数和方差两个因素分析,应选( )
甲 乙
平均数 9 8
方差 1 1
A.甲 B.乙 C.丙 D.丁
C
链接中考
方差s2= ×[(5-7)2+(8-7)2+(7-7)2+(6-7)2+(9-7)2]=2
2. (绥化)在一次射击训练中,某名选手五次射击的环数分别为5,8,7,6,9,则这名选手五次射击环数的方差为________.
2
五次射击的平均成绩为: ×(5+8+7+6+9)=7,
链接中考
2. 一组数据:a,a,a,…,a (有n个a)则它的方差为_____.
1. 有5个数1,4,a,5,2的平均数是a,则这5个数的方差是______.
2
0
3. 已知一组数据的方差是2,如果每个数据都加3得到一组新数据,则新数据的方差是______.
2
随堂检测
4. 已知一组数据的方差是2,如果每个数据都乘3得到一组新数据,则新数据的方差是______.
18
5. 甲、乙两名战士在射击训练中,打靶的次数相同,且射击成绩的平均数也相同,如果甲的射击成绩比较稳定,那么方差的大小关系是:s2甲______s2乙.
<
随堂检测
6. 小明本期五次测验的数学和英语成绩分别如下(单位:分)
数学 70 95 75 95 90
英语 80 85 90 85 85
通过对小明的两科成绩进行分析,你有何看法?对小明的学习你有什么建议?
平均数:都是85
方差:①数学 115;②英语 10
英语较稳定但要提高;数学不够稳定有待努力进步!
随堂检测
方差
课堂小结
公式:
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
