人教版八年级数学下册第十八章平行四边形 中位线在四边形中的应用 课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册第十八章平行四边形 中位线在四边形中的应用 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
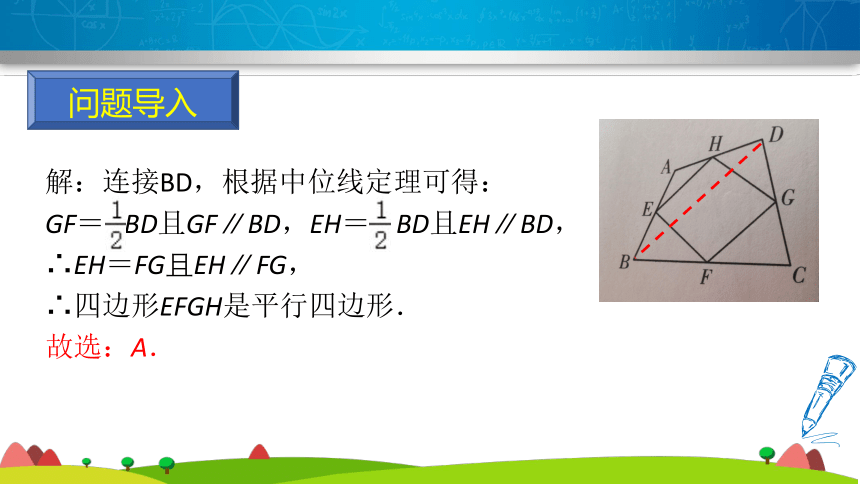
问题导入
问题:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH是( )
A.平行四边形
B.对角线互相垂直的四边形
C.矩形
D.菱形
选自《高分突破》学案本P46
问题导入
解:连接BD,根据中位线定理可得:
GF= BD且GF // BD,EH= BD且EH // BD,
∴EH=FG且EH // FG,
∴四边形EFGH是平行四边形.
故选:A.
问题导入
问题:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH是( )
A.平行四边形 B.对角线互相垂直的四边形
C.矩形 D.菱形
追问:如果把四边形ABCD改为平行四边形
或矩形或菱形等等一些特殊的四边形,
结论又会出现什么不同的情况呢?
中位线在四边形中的应用
1
知识点
三角形中位线的定义
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE. 像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
知识回顾
追问1:三角形有多少条边?每边都有几个中点?
追问2:一个三角形有多少条中位线?
2
知识点
三角形的中位线定理
知识回顾
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
要点精析:
三角形的中位线定理反映了三角形的中位线与第三边的双重关系:一是位置关系,可以用来证两直线平行;二是数量关系,可以用来证线段的倍分关系.
符号语言:
∵ D、E分别是AB、AC的中点.
∴ DE//BC, DE= BC.
1、如图,在△ABC中,∠ACB=90°,
AC=8,AB=10,DE垂直平分AC交AB
于点E,则DE的长为( )
A.6 B.5 C.4 D.3
D
牛刀小试
2、 如图,在△ABC中,点D,E分别是边 AB,BC的中点.若△DBE的周长是6,则 △ABC的周长是( )
A.8 B.10 C.12 D.14
C
牛刀小试
合作探究
1、顺次连接梯形各边中点所组成的图形是( )
A.平行四边形 B.菱形 C.梯形 D.正方形
2、顺次连接菱形四边中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
3、如图,四边形ABCD中,AC=BD,顺次连接四边形各边中点得到的图形是( )
A.菱形 B.矩形 C.正方形 D.以上都不对
合作探究
1、顺次连接梯形各边中点所组成的图形是( )
A.平行四边形 B.菱形 C.梯形 D.正方形
1、解:连接AC、BD,
∵E是AD的中点,H是CD的中点,
∴EH= AC,
同理FG= AC,
∴EH=FG,
同理EF=HG,
∴四边形EFGH是平行四边形,
故选:A.
追问:如果把“梯形”
改为“等腰梯形”呢?
合作探究
2、顺次连结菱形四边中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2、解:如图,四边形ABCD是菱形,且E、F、G、 H分别是AB、BC、CD、AD的中点,
则EH // FG // BD,EF=FG= BD;EF // HG // AC,EF=HG= AC,AC⊥BD.
故四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EH⊥EF,∠HEF=90°
∴边形EFGH是矩形.
故选:B.
合作探究
3、解:∵E,F分别是DC,AD的中点,
∴EF= AC,EF // AC,
同理,GH= AC,GH // AC,GF= BD,
∴EF=GH,EF // GH,
∴四边形EFGH是平行四边形,
∵AC=BD,
∴EF=GF,
∴平行四边形EFGH为菱形,
故选:A.
3、如图,四边形ABCD中,AC=BD,顺次连结四边形各边中点得到的图形是( )
A.菱形 B.矩形 C.正方形 D.以上都不对
归纳总结
利用三角形的中位线定理的关键在于找到
三角形和中点
“遇到中点,联想中位线”是一个解题突破口
应用与提高
1、任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC=20cm,BD=30cm,则四边形EFGH的周长是( )
A.80cm B.70cm
C.60cm D.50cm
应用与提高
解:∵E,F,G,H是四边形ABCD各边中点,
∴HG= AC,EF= AC,GF=HE= BD.
又∵AC=20cm,BD=30cm,
∴四边形EFGH的周长是HG+EF+GF+HE
= AC+ AC+ BD+ BD
=AC+BD
=50cm
故选:D.
应用与提高
2、如图,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( ).
(A)线段EF的长逐渐增大
(B)线段EF的长逐渐减小
(C)线段EF的长不变
(D)线段EF的长与点P的位置有关
应用与提高
追问:如图,已知四边形ABCD中,AB ⊥ BC,R、P分别是BC、CD上的动点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R在BC上从B向C移动时,问在什么时候EF的长度最大.
B
课后练习
若四边形的两条对角线相等且互相垂直,则顺次连接该四边形各边中点所得的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
课后练习
解:∵E、F、G、H分别为各边的中点,
∴EF // AC,GH // AC,EH // BD,FG // BD,
∴四边形EFGH是平行四边形,
∵AC⊥BD,EF // AC,EH // BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形,
∴∠MEN=90°,
∴四边形EFGH是矩形,
∵BD=AC,
∴EF=EH,
∴矩形EFGH是正方形.
故选:D.
问题导入
问题:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH是( )
A.平行四边形
B.对角线互相垂直的四边形
C.矩形
D.菱形
选自《高分突破》学案本P46
问题导入
解:连接BD,根据中位线定理可得:
GF= BD且GF // BD,EH= BD且EH // BD,
∴EH=FG且EH // FG,
∴四边形EFGH是平行四边形.
故选:A.
问题导入
问题:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH是( )
A.平行四边形 B.对角线互相垂直的四边形
C.矩形 D.菱形
追问:如果把四边形ABCD改为平行四边形
或矩形或菱形等等一些特殊的四边形,
结论又会出现什么不同的情况呢?
中位线在四边形中的应用
1
知识点
三角形中位线的定义
如图,在△ABC中,D,E分别是AB,AC的中点,连接DE. 像DE这样,连接三角形两边中点的线段叫做三角形的中位线.
知识回顾
追问1:三角形有多少条边?每边都有几个中点?
追问2:一个三角形有多少条中位线?
2
知识点
三角形的中位线定理
知识回顾
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
要点精析:
三角形的中位线定理反映了三角形的中位线与第三边的双重关系:一是位置关系,可以用来证两直线平行;二是数量关系,可以用来证线段的倍分关系.
符号语言:
∵ D、E分别是AB、AC的中点.
∴ DE//BC, DE= BC.
1、如图,在△ABC中,∠ACB=90°,
AC=8,AB=10,DE垂直平分AC交AB
于点E,则DE的长为( )
A.6 B.5 C.4 D.3
D
牛刀小试
2、 如图,在△ABC中,点D,E分别是边 AB,BC的中点.若△DBE的周长是6,则 △ABC的周长是( )
A.8 B.10 C.12 D.14
C
牛刀小试
合作探究
1、顺次连接梯形各边中点所组成的图形是( )
A.平行四边形 B.菱形 C.梯形 D.正方形
2、顺次连接菱形四边中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
3、如图,四边形ABCD中,AC=BD,顺次连接四边形各边中点得到的图形是( )
A.菱形 B.矩形 C.正方形 D.以上都不对
合作探究
1、顺次连接梯形各边中点所组成的图形是( )
A.平行四边形 B.菱形 C.梯形 D.正方形
1、解:连接AC、BD,
∵E是AD的中点,H是CD的中点,
∴EH= AC,
同理FG= AC,
∴EH=FG,
同理EF=HG,
∴四边形EFGH是平行四边形,
故选:A.
追问:如果把“梯形”
改为“等腰梯形”呢?
合作探究
2、顺次连结菱形四边中点所得的四边形一定是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
2、解:如图,四边形ABCD是菱形,且E、F、G、 H分别是AB、BC、CD、AD的中点,
则EH // FG // BD,EF=FG= BD;EF // HG // AC,EF=HG= AC,AC⊥BD.
故四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EH⊥EF,∠HEF=90°
∴边形EFGH是矩形.
故选:B.
合作探究
3、解:∵E,F分别是DC,AD的中点,
∴EF= AC,EF // AC,
同理,GH= AC,GH // AC,GF= BD,
∴EF=GH,EF // GH,
∴四边形EFGH是平行四边形,
∵AC=BD,
∴EF=GF,
∴平行四边形EFGH为菱形,
故选:A.
3、如图,四边形ABCD中,AC=BD,顺次连结四边形各边中点得到的图形是( )
A.菱形 B.矩形 C.正方形 D.以上都不对
归纳总结
利用三角形的中位线定理的关键在于找到
三角形和中点
“遇到中点,联想中位线”是一个解题突破口
应用与提高
1、任意四边形ABCD各边中点分别是E、F、G、H,若对角线AC=20cm,BD=30cm,则四边形EFGH的周长是( )
A.80cm B.70cm
C.60cm D.50cm
应用与提高
解:∵E,F,G,H是四边形ABCD各边中点,
∴HG= AC,EF= AC,GF=HE= BD.
又∵AC=20cm,BD=30cm,
∴四边形EFGH的周长是HG+EF+GF+HE
= AC+ AC+ BD+ BD
=AC+BD
=50cm
故选:D.
应用与提高
2、如图,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( ).
(A)线段EF的长逐渐增大
(B)线段EF的长逐渐减小
(C)线段EF的长不变
(D)线段EF的长与点P的位置有关
应用与提高
追问:如图,已知四边形ABCD中,AB ⊥ BC,R、P分别是BC、CD上的动点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R在BC上从B向C移动时,问在什么时候EF的长度最大.
B
课后练习
若四边形的两条对角线相等且互相垂直,则顺次连接该四边形各边中点所得的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
课后练习
解:∵E、F、G、H分别为各边的中点,
∴EF // AC,GH // AC,EH // BD,FG // BD,
∴四边形EFGH是平行四边形,
∵AC⊥BD,EF // AC,EH // BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形,
∴∠MEN=90°,
∴四边形EFGH是矩形,
∵BD=AC,
∴EF=EH,
∴矩形EFGH是正方形.
故选:D.
