人教版八年级下册 19.2.2 一次函数课件(共14张PPT)
文档属性
| 名称 | 人教版八年级下册 19.2.2 一次函数课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 103.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 21:36:11 | ||
图片预览






文档简介
(共14张PPT)
19.2 函数
19.2.2 一次函数
第4课时 一次函数与实际问题
复习导入
1.什么是一次函数?确定一个一次函数需要几个因素?是哪几个?
y=kx+b(k≠0)叫做关于x的一次函数,其中k和b为常数.这样在一次函数中,只要确定了k和b的值,那么这个一次函数也就随之确定了.可以说k和b是确定一次函数的两个因素.
2.已知一次函数y=2x+1,x取何值时,函数值y=3?
令y=3,代入解析式,得3=2x+1,解得x=1.
复习导入
3.从“形”的角度说“直线y=3x+4经过点(-1,1)”,把它改为从“数”的角度来叙述.
点(-1,1)满足解析式y=3x+4.
“数”与“形”的相互转化,是数形结合思想的体现.
合作探究
例1 已知AB两地相距90千米.某人骑自行车由A地去B地,他平均时速为15千米.
(1)求骑车人与终点B之间的距离y(千米)与出发时间x(小时)之间的函数关系;(2)画出函数图象.
分析:在这个问题中有两个已知量.一个是两地之间的距离90千米,一个是骑车人的速度.而骑车人与终点的距离y及出发时间x则都是未知量.我们能否找到这两个已知量与两个未知量之间的等量关系呢?找到后还要把它写成函数的形式,即把y写在等号的左边,其他的量则写到等号的右边.
活动:探究一次函数与实际问题
合作探究
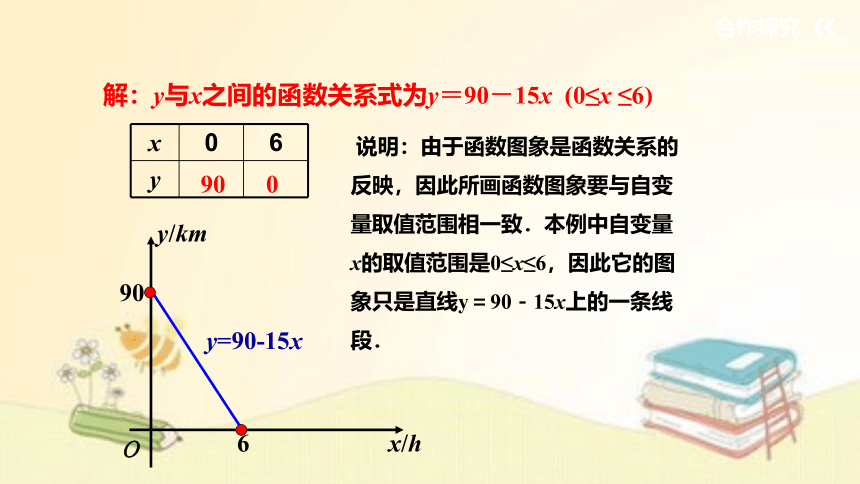
解:y与x之间的函数关系式为y=90-15x (0≤x ≤6)
x 0 6
y
y=90-15x
90
0
O
6
90
x/h
y/km
说明:由于函数图象是函数关系的反映,因此所画函数图象要与自变量取值范围相一致.本例中自变量x的取值范围是0≤x≤6,因此它的图象只是直线y=90-15x上的一条线段.
合作探究
例2 为了保护学生视力,课桌椅的高度都是按一定的关系配套设计的.研究表明:假设课桌的高度为ycm,椅子的高度(不含靠背)为xcm,则y应是x的一次函数.下表列出两套符合条件的课桌椅的高度:
第一套 第二套
椅子的高度x (cm) 40 37
桌子的高度y(cm) 75 70.2
(1) 求出y与x之间的函数关系式.
(2) 现有一把高42cm 的椅子和一张高为78.2cm 的课桌,它们是否配套?通过计算说明.
合作探究
分析:(1)由表中信息可知,当x=40时,y=75;当x=37时,y=70.2,因此可用待定系数法求出其函数解析式;(2)“是否配套”实际问题转为化数学问题就是问(42,78.2)这个点坐标是满足(1)中的解析式.
解:
(1)设y与x的函数关系式是y=kx+b.根据题意得
解得
40k+b=75
37k+b=70.2
k=1.6
b=11
∴y与x的函数关系式是y=1.6x+11.
(2)将x=42代入y=1.6x+11得
y=1.6×42+11=78.2
∴这套课桌椅是配套的.
合作探究
例3 甲乙两人同时从相距90km的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图,是他们离开A地的距离y(km)与x(h)之间的函数关系图象.
x/h
y/km
O
1
1.5
3
90
(1)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
合作探究
x/h
y/km
0
1
1.5
3
90
解:
设所求的函数关系式为y=kx+b,由图像可知,点(1.5,90),(3,0)满足该函数解析式,根据题意得
1.5k+b=90
3k+b=0
解得
k=-60
b=180
∴y=-60x+180
自变量的取值范围是
1.5≤x≤3.
合作探究
例3 甲乙两人同时从相距90km的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图,是他们离开A地的距离y(km)与x(h)之间的函数关系图象.
x/h
y/km
0
1
1.5
3
90
(2)若乙出发后2h和甲相遇,则乙从A地到B地用了多长时间?
合作探究
x/h
y/km
0
1
1.5
3
90
(2)若乙出发后2h和甲相遇,则乙从A地到B地用了多长时间?
解:当x=2时,代入y=-60x+180,得
y=-60×2+180=60
所以,图中相遇处该点坐标是(2,60)
因此可知乙的速度60÷2=30(km/h)
所以乙从A地到B地所用的时间是90÷30=3(h).
(2,60)
合作探究
解题小结:
解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
主要步骤如下:
(1)了解横纵轴的意义;
(2)从图象上判断函数与自变量的关系;
(3)抓住特殊点的实际意义.
课堂小结
1.本节课的学习了什么内容?
用待定系数法求一次函数的解析式 及利用函数图象解决实际问题.
2.待定系数法的主要步骤有哪几步?
(1)把某些未知的系数用字母表示;
(2)根据已知条件列出含有待定字母的方程或方程组.一般有几个待定字母应列几个方程;
(3)解方程或方程组求出待定字母的值,使问题得解
谢 谢!
19.2 函数
19.2.2 一次函数
第4课时 一次函数与实际问题
复习导入
1.什么是一次函数?确定一个一次函数需要几个因素?是哪几个?
y=kx+b(k≠0)叫做关于x的一次函数,其中k和b为常数.这样在一次函数中,只要确定了k和b的值,那么这个一次函数也就随之确定了.可以说k和b是确定一次函数的两个因素.
2.已知一次函数y=2x+1,x取何值时,函数值y=3?
令y=3,代入解析式,得3=2x+1,解得x=1.
复习导入
3.从“形”的角度说“直线y=3x+4经过点(-1,1)”,把它改为从“数”的角度来叙述.
点(-1,1)满足解析式y=3x+4.
“数”与“形”的相互转化,是数形结合思想的体现.
合作探究
例1 已知AB两地相距90千米.某人骑自行车由A地去B地,他平均时速为15千米.
(1)求骑车人与终点B之间的距离y(千米)与出发时间x(小时)之间的函数关系;(2)画出函数图象.
分析:在这个问题中有两个已知量.一个是两地之间的距离90千米,一个是骑车人的速度.而骑车人与终点的距离y及出发时间x则都是未知量.我们能否找到这两个已知量与两个未知量之间的等量关系呢?找到后还要把它写成函数的形式,即把y写在等号的左边,其他的量则写到等号的右边.
活动:探究一次函数与实际问题
合作探究
解:y与x之间的函数关系式为y=90-15x (0≤x ≤6)
x 0 6
y
y=90-15x
90
0
O
6
90
x/h
y/km
说明:由于函数图象是函数关系的反映,因此所画函数图象要与自变量取值范围相一致.本例中自变量x的取值范围是0≤x≤6,因此它的图象只是直线y=90-15x上的一条线段.
合作探究
例2 为了保护学生视力,课桌椅的高度都是按一定的关系配套设计的.研究表明:假设课桌的高度为ycm,椅子的高度(不含靠背)为xcm,则y应是x的一次函数.下表列出两套符合条件的课桌椅的高度:
第一套 第二套
椅子的高度x (cm) 40 37
桌子的高度y(cm) 75 70.2
(1) 求出y与x之间的函数关系式.
(2) 现有一把高42cm 的椅子和一张高为78.2cm 的课桌,它们是否配套?通过计算说明.
合作探究
分析:(1)由表中信息可知,当x=40时,y=75;当x=37时,y=70.2,因此可用待定系数法求出其函数解析式;(2)“是否配套”实际问题转为化数学问题就是问(42,78.2)这个点坐标是满足(1)中的解析式.
解:
(1)设y与x的函数关系式是y=kx+b.根据题意得
解得
40k+b=75
37k+b=70.2
k=1.6
b=11
∴y与x的函数关系式是y=1.6x+11.
(2)将x=42代入y=1.6x+11得
y=1.6×42+11=78.2
∴这套课桌椅是配套的.
合作探究
例3 甲乙两人同时从相距90km的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图,是他们离开A地的距离y(km)与x(h)之间的函数关系图象.
x/h
y/km
O
1
1.5
3
90
(1)求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
合作探究
x/h
y/km
0
1
1.5
3
90
解:
设所求的函数关系式为y=kx+b,由图像可知,点(1.5,90),(3,0)满足该函数解析式,根据题意得
1.5k+b=90
3k+b=0
解得
k=-60
b=180
∴y=-60x+180
自变量的取值范围是
1.5≤x≤3.
合作探究
例3 甲乙两人同时从相距90km的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图,是他们离开A地的距离y(km)与x(h)之间的函数关系图象.
x/h
y/km
0
1
1.5
3
90
(2)若乙出发后2h和甲相遇,则乙从A地到B地用了多长时间?
合作探究
x/h
y/km
0
1
1.5
3
90
(2)若乙出发后2h和甲相遇,则乙从A地到B地用了多长时间?
解:当x=2时,代入y=-60x+180,得
y=-60×2+180=60
所以,图中相遇处该点坐标是(2,60)
因此可知乙的速度60÷2=30(km/h)
所以乙从A地到B地所用的时间是90÷30=3(h).
(2,60)
合作探究
解题小结:
解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
主要步骤如下:
(1)了解横纵轴的意义;
(2)从图象上判断函数与自变量的关系;
(3)抓住特殊点的实际意义.
课堂小结
1.本节课的学习了什么内容?
用待定系数法求一次函数的解析式 及利用函数图象解决实际问题.
2.待定系数法的主要步骤有哪几步?
(1)把某些未知的系数用字母表示;
(2)根据已知条件列出含有待定字母的方程或方程组.一般有几个待定字母应列几个方程;
(3)解方程或方程组求出待定字母的值,使问题得解
谢 谢!
