北京版小学数学五下 4.2分数的基本性质 教案
文档属性
| 名称 | 北京版小学数学五下 4.2分数的基本性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:00:00 | ||
图片预览

文档简介
第1课时 分数的基本性质(1)
【教学目标】
1. 知识技能:通过教学,使学生归纳概括出分数的基本性质,并能理解分数的基本性质,正确运用分数的基本性质解题。
2. 数学思考:①对学生渗透数形结合的数学思想。
②培养学生的迁移能力、抽象概括能力和观察能力。
3. 问题解决:培养学生运用数形结合的思想方法解决问题,体会数形结合思想的优点。
4. 情感态度:让学生体会到数学知识的内在联系,感受学习数学知识的生动有趣。
【重点难点】重点:抽象概括出分数的基本性质。
难点:引导学生自主推导分数的基本性质的过程。
【教学准备】 学习单、彩色笔、每同桌三张圆形纸片
教学过程:
一、复习导入
1. 说出下列各分数的意义。
小结:一个分数的分母表示平均分的份数,分子表示取的份数。
2. 口算:小结分数与除法的关系。
2÷3= 12÷11= 5÷9= 10÷7=
4÷6= 4÷7= 4÷8= 4÷9=
板书:a÷b= (b≠0)
小结:除法的运算结果可以用分数来表示,说明分数与除法之间有着密切的联系。
3.商不变规律。
(1)计算: 3÷1= 12÷4= 24÷8= 240÷80=
(2)说一说,你有什么发现?
商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变。
除法有商不变的性质,那分数的性质是什么呢?这节课我们就来研究这个问题。
二、探究新知
1.三毛家有三兄弟,他们都特别爱吃饼。一天,妈妈买回3张同样大小的饼,准备平均分给他们吃。
妈妈先把第一张饼平均分成两份,取出其中的一份给大毛;二毛看见了,说:“太少了,我要吃两份。”妈妈点点头,把第二张饼平均分成四份,取出其中的两份给二毛;三毛连忙说:“我要更多,我要吃四份。”妈妈又点点头,把第三张饼平均分成了八份,取出其中的四份给三毛。想一想:三兄弟究竟谁吃得最多?(让学生猜猜)
2.动手实验,同桌合作。
(1)拿出3张同样大小的圆纸(饼),分别把它们平均分成2份、4份和8份。
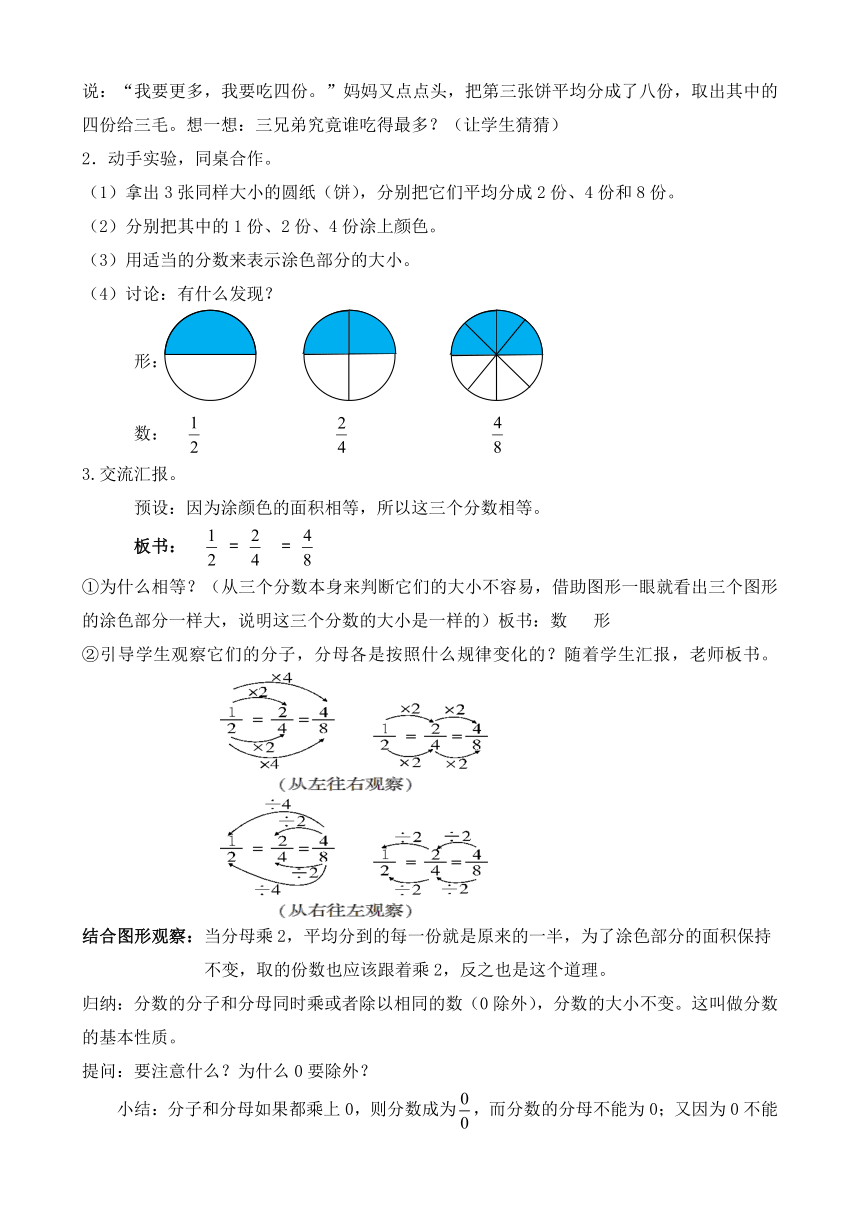
(2)分别把其中的1份、2份、4份涂上颜色。
(3)用适当的分数来表示涂色部分的大小。
(4)讨论:有什么发现?
形:
数:
3.交流汇报。
预设:因为涂颜色的面积相等,所以这三个分数相等。
板书: = =
①为什么相等?(从三个分数本身来判断它们的大小不容易,借助图形一眼就看出三个图形的涂色部分一样大,说明这三个分数的大小是一样的)板书:数 形
②引导学生观察它们的分子,分母各是按照什么规律变化的?随着学生汇报,老师板书。
结合图形观察:当分母乘2,平均分到的每一份就是原来的一半,为了涂色部分的面积保持
不变,取的份数也应该跟着乘2,反之也是这个道理。
归纳:分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
提问:要注意什么?为什么0要除外?
小结:分子和分母如果都乘上0,则分数成为,而分数的分母不能为0;又因为0不能作除数,所以分数的分子和分母也不能同时除以0。
4.提问:分数的基本性质和商不变的性质有什么联系?(分子相当于被除数,分母相当于除数。)
5.那么刚才三毛三兄弟分到的饼究竟谁大谁小?(一样大)
小结:虽然他们三人拿到的块数不一样,但吃到的饼的大小其实是一样的。他们的妈妈真聪明,利用分数的基本性质,既分得公平一样大,又满足了他们各自的愿望。
师:刚才我们要比较这三个分数的大小,借助了图形,先把圆平均分成2份、4份、8份,再分别把其中的1份、2份、4份涂上颜色,通过观察,很容易就看出其实这三个分数的大小是一样的,这种方法叫做数形结合。(板书:结合)你觉得这种方法有什么优点?你喜欢这种方法吗?以后我们也可以多用数形结合的方法来研究更多的数学知识。
三、巩固运用。
1. 涂色表示出与给定分数相等的分数。
你是根据什么来想的?(分数的基本性质)
2、判断每组中的两个分数是否相等?相等的在括号里画“√”,不相等的画“×”
和 ( ) 和 ( ) 和( ) 和( )
3、504班的同学参加合唱小组, 的同学参加足球小组,下面哪种说法对?
( )
A 参加合唱小组的人数多 B 参加足球小组的人数多 C 两个小组的人数同样多
4、在直线上表示出下列分数。
小结:在直线上同一点上的分数大小相同;反过来说,同一个点可以用不同的分数来表示。
5、按要求涂色,再比较它们的大小。
先只出示分数,问:你能很快比较出它们的大小吗?
生:很难,它们分子分母不相同,也没有明显的倍数关系。
再出示图:那给你们图形,先涂颜色,再判断,现在觉得难不难?
你想说什么?
小结:用数形结合的方法,一眼看出涂色的面积谁大谁小,就容易判断出分数的大小了。
刚才我们判断出 = 你们还能说出跟这两个分数一样大的分数吗 说得玩吗?
小结:大小相等的分数有无数个。
四、畅谈收获:通过这节课的学习,你学会了什么?有什么收获呢?
板书设计:
第1课时 分数的基本性质(1)
0
1
【教学目标】
1. 知识技能:通过教学,使学生归纳概括出分数的基本性质,并能理解分数的基本性质,正确运用分数的基本性质解题。
2. 数学思考:①对学生渗透数形结合的数学思想。
②培养学生的迁移能力、抽象概括能力和观察能力。
3. 问题解决:培养学生运用数形结合的思想方法解决问题,体会数形结合思想的优点。
4. 情感态度:让学生体会到数学知识的内在联系,感受学习数学知识的生动有趣。
【重点难点】重点:抽象概括出分数的基本性质。
难点:引导学生自主推导分数的基本性质的过程。
【教学准备】 学习单、彩色笔、每同桌三张圆形纸片
教学过程:
一、复习导入
1. 说出下列各分数的意义。
小结:一个分数的分母表示平均分的份数,分子表示取的份数。
2. 口算:小结分数与除法的关系。
2÷3= 12÷11= 5÷9= 10÷7=
4÷6= 4÷7= 4÷8= 4÷9=
板书:a÷b= (b≠0)
小结:除法的运算结果可以用分数来表示,说明分数与除法之间有着密切的联系。
3.商不变规律。
(1)计算: 3÷1= 12÷4= 24÷8= 240÷80=
(2)说一说,你有什么发现?
商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变。
除法有商不变的性质,那分数的性质是什么呢?这节课我们就来研究这个问题。
二、探究新知
1.三毛家有三兄弟,他们都特别爱吃饼。一天,妈妈买回3张同样大小的饼,准备平均分给他们吃。
妈妈先把第一张饼平均分成两份,取出其中的一份给大毛;二毛看见了,说:“太少了,我要吃两份。”妈妈点点头,把第二张饼平均分成四份,取出其中的两份给二毛;三毛连忙说:“我要更多,我要吃四份。”妈妈又点点头,把第三张饼平均分成了八份,取出其中的四份给三毛。想一想:三兄弟究竟谁吃得最多?(让学生猜猜)
2.动手实验,同桌合作。
(1)拿出3张同样大小的圆纸(饼),分别把它们平均分成2份、4份和8份。
(2)分别把其中的1份、2份、4份涂上颜色。
(3)用适当的分数来表示涂色部分的大小。
(4)讨论:有什么发现?
形:
数:
3.交流汇报。
预设:因为涂颜色的面积相等,所以这三个分数相等。
板书: = =
①为什么相等?(从三个分数本身来判断它们的大小不容易,借助图形一眼就看出三个图形的涂色部分一样大,说明这三个分数的大小是一样的)板书:数 形
②引导学生观察它们的分子,分母各是按照什么规律变化的?随着学生汇报,老师板书。
结合图形观察:当分母乘2,平均分到的每一份就是原来的一半,为了涂色部分的面积保持
不变,取的份数也应该跟着乘2,反之也是这个道理。
归纳:分数的分子和分母同时乘或者除以相同的数(0除外),分数的大小不变。这叫做分数的基本性质。
提问:要注意什么?为什么0要除外?
小结:分子和分母如果都乘上0,则分数成为,而分数的分母不能为0;又因为0不能作除数,所以分数的分子和分母也不能同时除以0。
4.提问:分数的基本性质和商不变的性质有什么联系?(分子相当于被除数,分母相当于除数。)
5.那么刚才三毛三兄弟分到的饼究竟谁大谁小?(一样大)
小结:虽然他们三人拿到的块数不一样,但吃到的饼的大小其实是一样的。他们的妈妈真聪明,利用分数的基本性质,既分得公平一样大,又满足了他们各自的愿望。
师:刚才我们要比较这三个分数的大小,借助了图形,先把圆平均分成2份、4份、8份,再分别把其中的1份、2份、4份涂上颜色,通过观察,很容易就看出其实这三个分数的大小是一样的,这种方法叫做数形结合。(板书:结合)你觉得这种方法有什么优点?你喜欢这种方法吗?以后我们也可以多用数形结合的方法来研究更多的数学知识。
三、巩固运用。
1. 涂色表示出与给定分数相等的分数。
你是根据什么来想的?(分数的基本性质)
2、判断每组中的两个分数是否相等?相等的在括号里画“√”,不相等的画“×”
和 ( ) 和 ( ) 和( ) 和( )
3、504班的同学参加合唱小组, 的同学参加足球小组,下面哪种说法对?
( )
A 参加合唱小组的人数多 B 参加足球小组的人数多 C 两个小组的人数同样多
4、在直线上表示出下列分数。
小结:在直线上同一点上的分数大小相同;反过来说,同一个点可以用不同的分数来表示。
5、按要求涂色,再比较它们的大小。
先只出示分数,问:你能很快比较出它们的大小吗?
生:很难,它们分子分母不相同,也没有明显的倍数关系。
再出示图:那给你们图形,先涂颜色,再判断,现在觉得难不难?
你想说什么?
小结:用数形结合的方法,一眼看出涂色的面积谁大谁小,就容易判断出分数的大小了。
刚才我们判断出 = 你们还能说出跟这两个分数一样大的分数吗 说得玩吗?
小结:大小相等的分数有无数个。
四、畅谈收获:通过这节课的学习,你学会了什么?有什么收获呢?
板书设计:
第1课时 分数的基本性质(1)
0
1
