沪科版数学七年级下册10.3平行线的性质(第2课时平行线性质与判定综合)课件(共25张PPT)
文档属性
| 名称 | 沪科版数学七年级下册10.3平行线的性质(第2课时平行线性质与判定综合)课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 896.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 11:21:40 | ||
图片预览




文档简介
(共25张PPT)
沪科版数学七年级下册
10.3 平行线的性质
第二课时
学习目标
理解平行线的性质与判定的区别,并初步学会数学说理
1
通过平行线的性质与判定的对比,培养学生观察和分析能力以及有条理的表达能力
2
在探究问题的基础上体验数学思考过程的条理性和解决问题的多样性,并形成反思的习惯
3
知识回顾
请填写下列表格
平行线的性质 平行线的判定
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
思考
平行线的性质与判定有什么区别和联系?
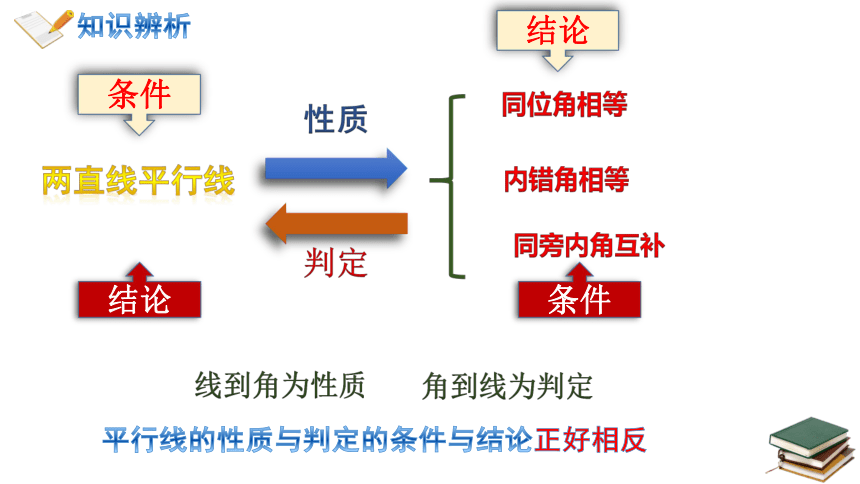
平行线的性质与判定的条件与结论正好相反
两直线平行线
同位角相等
内错角相等
同旁内角互补
性质
判定
线到角为性质
角到线为判定
知识辨析
条件
结论
结论
条件
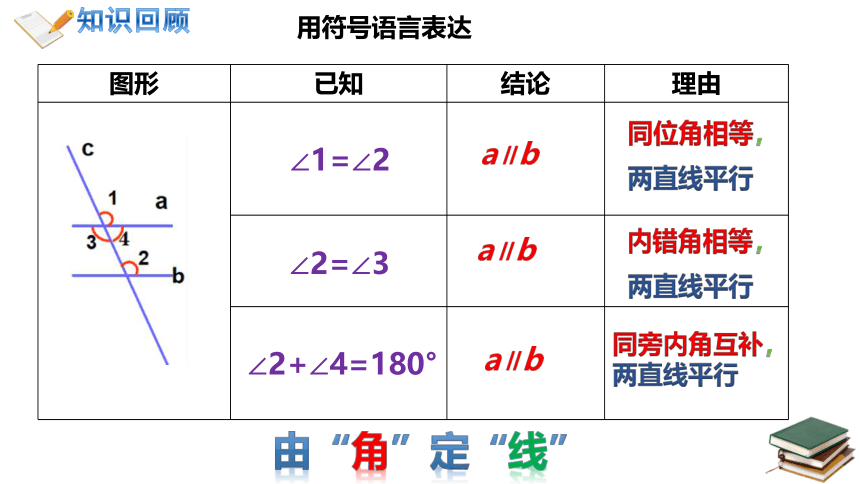
图形 已知 结论 理由
用符号语言表达
同位角相等,
两直线平行
a∥b
内错角相等,
两直线平行
∠2+∠4=180°
由“角”定“线”
知识回顾
∠1=∠2
∠2=∠3
a∥b
a∥b
同旁内角互补,两直线平行
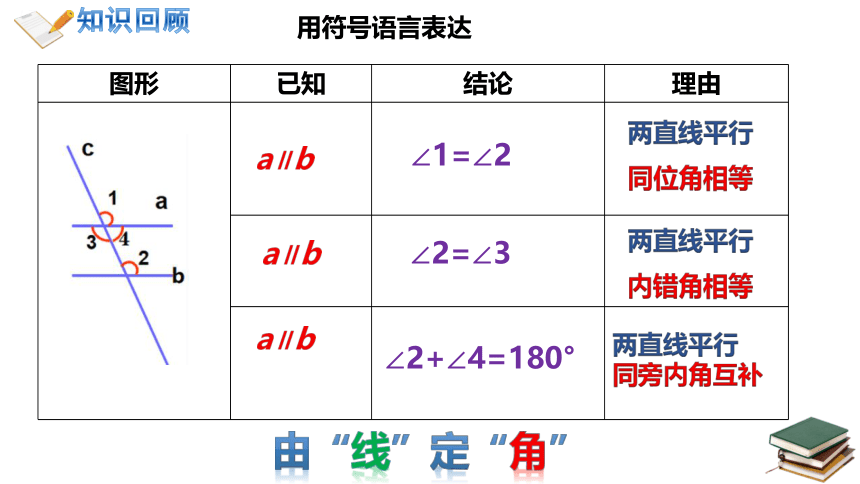
图形 已知 结论 理由
两直线平行
同位角相等
a∥b
两直线平行
内错角相等
∠2+∠4=180°
由“线”定“角”
知识回顾
∠1=∠2
∠2=∠3
a∥b
a∥b
两直线平行
同旁内角互补
用符号语言表达
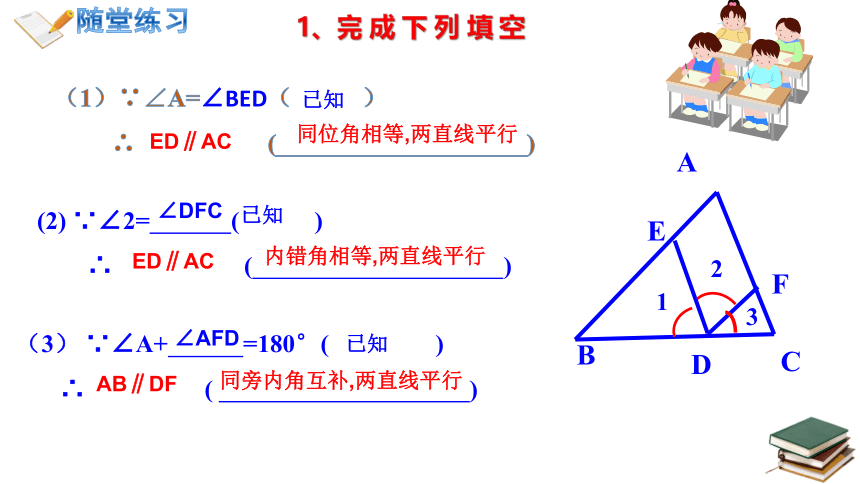
随堂练习
1、完 成 下 列 填 空
A
B
E
F
D
C
1
2
3
(1)∵∠A=∠BED( )
∴ ( )
同位角相等,两直线平行
ED∥AC
已知
(2) ∵∠2= ( )
∴ ( )
∠DFC
已知
内错角相等,两直线平行
ED∥AC
(3) ∵∠A+ =180°( )
∴ ( )
∠AFD
同旁内角互补,两直线平行
AB∥DF
已知
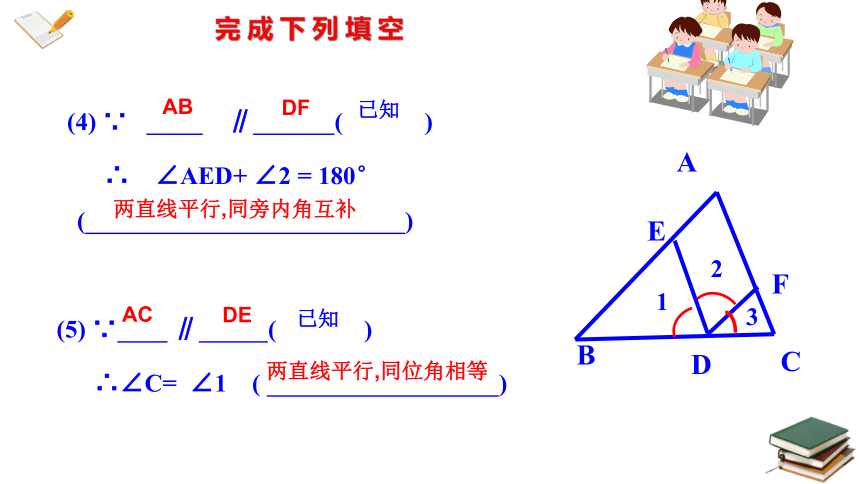
完 成 下 列 填 空
A
B
E
F
D
C
1
2
3
(4) ∵ ∥ ( )
∴ ∠AED+ ∠2 = 180° ( )
DF
已知
两直线平行,同旁内角互补
AB
(5) ∵ ∥ ( )
∴∠C= ∠1 ( )
DE
已知
两直线平行,同位角相等
AC
已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:
因为 ∠1=∠2
所以 AB∥EF
(内错角相等,两直线平行).
(已知),
因为 AB⊥BF,CD⊥BF,
所以 AB∥CD
所以 EF∥CD
所以 ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,内错角相等).
例1
例题精讲
因为
∵
所以
∴
∵
∴
∴
∴
∴
∵
如图,A、B、C三点在同一直线上,∠1 =∠2 , ∠3 =∠D,试说明BD∥CE。
A
B
C
D
E
1
2
3
解:
∵∠1=∠2(已知)
∴AD∥BE
(内错角相等,两直线平行)
∴∠D=∠4
(两直线平行,内错角相等)
又∵∠D=∠3(已知)
∴∠3=∠4
∴BD∥CE
(等量代换)
(内错角相等,两直线平行)
4
例题精讲
例2
知识点
平行线性质和判定的综合应用
例题精讲
如图AB∥DE,试说明∠B+∠E=∠BCE
例3
A
B
C
D
1
2
F
E
证明:
过点C作CF∥AB
∴∠B=∠1
(两直线平行,内错角相等)
∵AB∥DE,AB∥CF
∴CF∥DE
(平行于同一直线的两条直线互相平行)
∴∠E=∠2
(两直线平行,内错角相等)
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE
知识点
辅助线:为帮助解题而添加的线
辅助线一般画成虚线
如图,AB∥DE,那么∠B、∠BCD、∠D 有什么关系?
A
B
C
D
E
F
过C作CF∥AB
∴∠B+∠BCD=180+∠D
以上两题有什么共同特点?
1、过转折点作平行线
2、利用平行线相关性质
1
2
变式练习1
证明:
∴∠D=∠1
∴∠B+∠2=180°
∴∠B+∠2+∠1=180°+∠D
∴∠B+∠BCD-∠D=180
变式练习2
如图,AD∥BC,∠A=120°、∠B=140°,求∠AEB的大小
F
A
B
C
D
E
过E作EF∥AD
证明:
1
2
∴∠A+∠AEF=180°
∵∠A=120°
∴∠AEF=60°
即∠1+∠2=60°
∵AD∥BC
∴BC∥EF
∴∠1+∠EBC=180°
∵∠EBC=140°
∴∠1=40°
∴∠2=60°-∠1=20°
辅助线:
过转折点作平行线
如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
实际应用
已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.试说明:PM∥NQ.
理由如下: ∵AB∥CD
∴2=∠3.(两直线平行,内错角相等)
∵∠1=∠2 ,∠3=∠4,
∴∠1=∠2 =∠3=∠4.
∵∠1+∠2 +∠5=180 ,
∠3+∠4 +∠6=180 ,
∴∠5=∠6.
∴ PM∥NQ (内错角相等,两直线平行).
实际应用
解:
1.如图,∠A=∠D,如果∠B=20°,那么∠C
为( )
A.40° B.20°
C.60° D.70°
解: ∵∠A=∠D,∴AB∥CD.
∵AB∥CD,∠B=20°,
∴ ∠C=∠B=20°.
B
课堂 练习
D
A
B
C
2.如图,直线a,b与直线c,d相交,若∠1=∠2,
∠3=70°,则∠4的度数是( )
A.35° B.70°
C.90° D.110°
D
课堂 练习
解析:
∵∠1=∠2,
∴a∥b,
∴∠3=∠5 =70°.
∴∠4=180°-70°=110°.
3.如图,AE∥CD,若∠1=37°,∠D=54°,则∠2= ° ,∠BAE= ° 。
解:∵AE∥CD,
∴∠2=∠1=37°.
∴∠BAE=∠D=54°.
54
37
课堂 练习
课堂 练习
4、如图,衣服三角尺如图放置,两只脚吃的斜边互相平行,每个直角尺的直角顶点都在另一个直角尺的斜边上,图中∠α= 度(2021烟台中考)
α
75
5、一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 度.
解:过B作BF∥AE,则CD∥BF∥AE,
∴∠BCD+∠CBF=180°.
∵AB⊥AE,∴AB⊥BF,∴∠ABF =90°,
∴∠ABC+∠BCD=90°+180°=270°.
270
课堂 练习
B
C
D
F
辅助线:
过转折点作平行线
6、如图, ∠B=∠C ∠B+∠D=180°, 那么BC平行DE吗?为什么?
A
B
C
D
E
答:BC∥DE
理由如下:
∵ ∠B=∠C ( )
已知
∠B+ ∠D=180°( )
已知
∴ ∠C+ ∠D=180°( )
等量代换
∴BC∥DE( )
同旁内角互补,两直线平行
课堂练习
理由如下:
∵ BE平分∠ABC,
∴
同理
∵ AB∥CD,
∴∠ABC=∠BCD.
∴∠1=∠2.
∵∠1和∠2是内错角,
∴ BE∥CF(内错角相等,两直线平行).
1
2
1、如图,AB∥CD,BE平分∠ABC,CF平分∠BCD,你能发现BE与CF的位置关系吗?说明理由.
答: BE∥CF.
巩固练习
2、如图EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数。
解:
∵EF∥AD
(已知)
∴∠2=∠3
又∵∠1=∠2
∴∠1=∠3
∴DG∥AB
∴∠BAC+∠AGD=180°
∴∠AGD=180°-∠BAC=180°-70°=110°
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
?
巩固练习
提升练习
如图, ∠1=∠2, ∠AEB+∠DEB=180°, 那么∠F与∠G相等吗?为什么?
A
B
C
D
E
G
F
1
2
答:∠F=∠G.理由如下
∵∠AEB+∠DEB=180°
∴AC∥DE
∴∠EBC=∠BED.
∴∠1+∠EBF=∠2+∠BEG.
∵∠1=∠2
∴∠EBF=∠BEG.
∴BF∥GE
∴∠F=∠G
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
小结
课堂小结
沪科版数学七年级下册
10.3 平行线的性质
第二课时
学习目标
理解平行线的性质与判定的区别,并初步学会数学说理
1
通过平行线的性质与判定的对比,培养学生观察和分析能力以及有条理的表达能力
2
在探究问题的基础上体验数学思考过程的条理性和解决问题的多样性,并形成反思的习惯
3
知识回顾
请填写下列表格
平行线的性质 平行线的判定
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
思考
平行线的性质与判定有什么区别和联系?
平行线的性质与判定的条件与结论正好相反
两直线平行线
同位角相等
内错角相等
同旁内角互补
性质
判定
线到角为性质
角到线为判定
知识辨析
条件
结论
结论
条件
图形 已知 结论 理由
用符号语言表达
同位角相等,
两直线平行
a∥b
内错角相等,
两直线平行
∠2+∠4=180°
由“角”定“线”
知识回顾
∠1=∠2
∠2=∠3
a∥b
a∥b
同旁内角互补,两直线平行
图形 已知 结论 理由
两直线平行
同位角相等
a∥b
两直线平行
内错角相等
∠2+∠4=180°
由“线”定“角”
知识回顾
∠1=∠2
∠2=∠3
a∥b
a∥b
两直线平行
同旁内角互补
用符号语言表达
随堂练习
1、完 成 下 列 填 空
A
B
E
F
D
C
1
2
3
(1)∵∠A=∠BED( )
∴ ( )
同位角相等,两直线平行
ED∥AC
已知
(2) ∵∠2= ( )
∴ ( )
∠DFC
已知
内错角相等,两直线平行
ED∥AC
(3) ∵∠A+ =180°( )
∴ ( )
∠AFD
同旁内角互补,两直线平行
AB∥DF
已知
完 成 下 列 填 空
A
B
E
F
D
C
1
2
3
(4) ∵ ∥ ( )
∴ ∠AED+ ∠2 = 180° ( )
DF
已知
两直线平行,同旁内角互补
AB
(5) ∵ ∥ ( )
∴∠C= ∠1 ( )
DE
已知
两直线平行,同位角相等
AC
已知AB⊥BF,CD⊥BF,∠1= ∠2,试说明∠3=∠E.
A
B
C
D
E
F
1
2
3
解:
因为 ∠1=∠2
所以 AB∥EF
(内错角相等,两直线平行).
(已知),
因为 AB⊥BF,CD⊥BF,
所以 AB∥CD
所以 EF∥CD
所以 ∠3= ∠E
(垂直于同一条直线的两条直线平行).
(平行于同一条直线的两条直线平行).
(两直线平行,内错角相等).
例1
例题精讲
因为
∵
所以
∴
∵
∴
∴
∴
∴
∵
如图,A、B、C三点在同一直线上,∠1 =∠2 , ∠3 =∠D,试说明BD∥CE。
A
B
C
D
E
1
2
3
解:
∵∠1=∠2(已知)
∴AD∥BE
(内错角相等,两直线平行)
∴∠D=∠4
(两直线平行,内错角相等)
又∵∠D=∠3(已知)
∴∠3=∠4
∴BD∥CE
(等量代换)
(内错角相等,两直线平行)
4
例题精讲
例2
知识点
平行线性质和判定的综合应用
例题精讲
如图AB∥DE,试说明∠B+∠E=∠BCE
例3
A
B
C
D
1
2
F
E
证明:
过点C作CF∥AB
∴∠B=∠1
(两直线平行,内错角相等)
∵AB∥DE,AB∥CF
∴CF∥DE
(平行于同一直线的两条直线互相平行)
∴∠E=∠2
(两直线平行,内错角相等)
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE
知识点
辅助线:为帮助解题而添加的线
辅助线一般画成虚线
如图,AB∥DE,那么∠B、∠BCD、∠D 有什么关系?
A
B
C
D
E
F
过C作CF∥AB
∴∠B+∠BCD=180+∠D
以上两题有什么共同特点?
1、过转折点作平行线
2、利用平行线相关性质
1
2
变式练习1
证明:
∴∠D=∠1
∴∠B+∠2=180°
∴∠B+∠2+∠1=180°+∠D
∴∠B+∠BCD-∠D=180
变式练习2
如图,AD∥BC,∠A=120°、∠B=140°,求∠AEB的大小
F
A
B
C
D
E
过E作EF∥AD
证明:
1
2
∴∠A+∠AEF=180°
∵∠A=120°
∴∠AEF=60°
即∠1+∠2=60°
∵AD∥BC
∴BC∥EF
∴∠1+∠EBC=180°
∵∠EBC=140°
∴∠1=40°
∴∠2=60°-∠1=20°
辅助线:
过转折点作平行线
如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
实际应用
已知条件:如图,AB∥CD,∠1=∠2,∠3=∠4.试说明:PM∥NQ.
理由如下: ∵AB∥CD
∴2=∠3.(两直线平行,内错角相等)
∵∠1=∠2 ,∠3=∠4,
∴∠1=∠2 =∠3=∠4.
∵∠1+∠2 +∠5=180 ,
∠3+∠4 +∠6=180 ,
∴∠5=∠6.
∴ PM∥NQ (内错角相等,两直线平行).
实际应用
解:
1.如图,∠A=∠D,如果∠B=20°,那么∠C
为( )
A.40° B.20°
C.60° D.70°
解: ∵∠A=∠D,∴AB∥CD.
∵AB∥CD,∠B=20°,
∴ ∠C=∠B=20°.
B
课堂 练习
D
A
B
C
2.如图,直线a,b与直线c,d相交,若∠1=∠2,
∠3=70°,则∠4的度数是( )
A.35° B.70°
C.90° D.110°
D
课堂 练习
解析:
∵∠1=∠2,
∴a∥b,
∴∠3=∠5 =70°.
∴∠4=180°-70°=110°.
3.如图,AE∥CD,若∠1=37°,∠D=54°,则∠2= ° ,∠BAE= ° 。
解:∵AE∥CD,
∴∠2=∠1=37°.
∴∠BAE=∠D=54°.
54
37
课堂 练习
课堂 练习
4、如图,衣服三角尺如图放置,两只脚吃的斜边互相平行,每个直角尺的直角顶点都在另一个直角尺的斜边上,图中∠α= 度(2021烟台中考)
α
75
5、一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 度.
解:过B作BF∥AE,则CD∥BF∥AE,
∴∠BCD+∠CBF=180°.
∵AB⊥AE,∴AB⊥BF,∴∠ABF =90°,
∴∠ABC+∠BCD=90°+180°=270°.
270
课堂 练习
B
C
D
F
辅助线:
过转折点作平行线
6、如图, ∠B=∠C ∠B+∠D=180°, 那么BC平行DE吗?为什么?
A
B
C
D
E
答:BC∥DE
理由如下:
∵ ∠B=∠C ( )
已知
∠B+ ∠D=180°( )
已知
∴ ∠C+ ∠D=180°( )
等量代换
∴BC∥DE( )
同旁内角互补,两直线平行
课堂练习
理由如下:
∵ BE平分∠ABC,
∴
同理
∵ AB∥CD,
∴∠ABC=∠BCD.
∴∠1=∠2.
∵∠1和∠2是内错角,
∴ BE∥CF(内错角相等,两直线平行).
1
2
1、如图,AB∥CD,BE平分∠ABC,CF平分∠BCD,你能发现BE与CF的位置关系吗?说明理由.
答: BE∥CF.
巩固练习
2、如图EF∥AD,∠1=∠2,∠BAC=70 °,求∠AGD的度数。
解:
∵EF∥AD
(已知)
∴∠2=∠3
又∵∠1=∠2
∴∠1=∠3
∴DG∥AB
∴∠BAC+∠AGD=180°
∴∠AGD=180°-∠BAC=180°-70°=110°
(两直线平行,同位角相等)
(已知)
(等量代换)
(内错角相等,两直线平行)
(两直线平行,同旁内角互补)
?
巩固练习
提升练习
如图, ∠1=∠2, ∠AEB+∠DEB=180°, 那么∠F与∠G相等吗?为什么?
A
B
C
D
E
G
F
1
2
答:∠F=∠G.理由如下
∵∠AEB+∠DEB=180°
∴AC∥DE
∴∠EBC=∠BED.
∴∠1+∠EBF=∠2+∠BEG.
∵∠1=∠2
∴∠EBF=∠BEG.
∴BF∥GE
∴∠F=∠G
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
小结
课堂小结
