8.1基本立体图形基础 练习卷(Word版含解析)
文档属性
| 名称 | 8.1基本立体图形基础 练习卷(Word版含解析) | 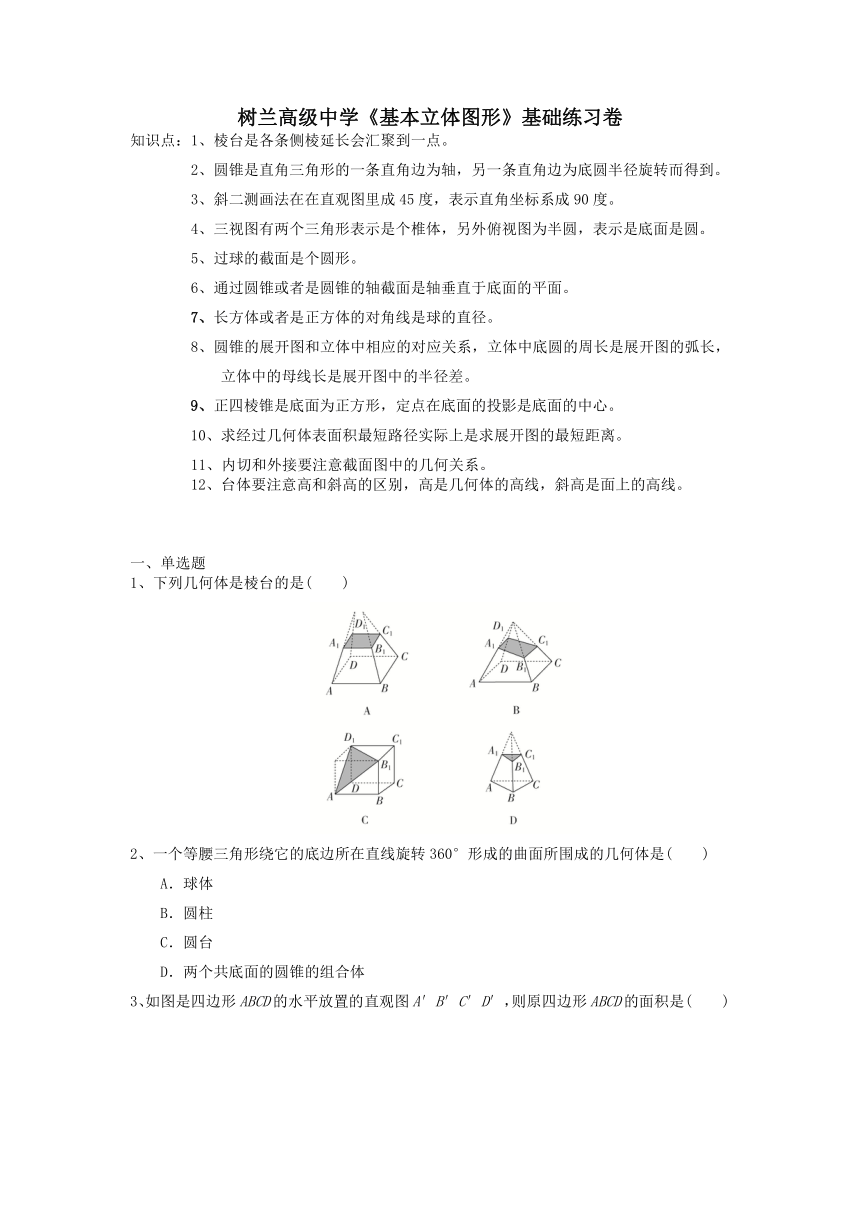 | |
| 格式 | docx | ||
| 文件大小 | 204.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 11:49:34 | ||
图片预览





文档简介
树兰高级中学《基本立体图形》基础练习卷
知识点:1、棱台是各条侧棱延长会汇聚到一点。
2、圆锥是直角三角形的一条直角边为轴,另一条直角边为底圆半径旋转而得到。
3、斜二测画法在在直观图里成45度,表示直角坐标系成90度。
4、三视图有两个三角形表示是个椎体,另外俯视图为半圆,表示是底面是圆。
5、过球的截面是个圆形。
6、通过圆锥或者是圆锥的轴截面是轴垂直于底面的平面。
7、长方体或者是正方体的对角线是球的直径。
8、圆锥的展开图和立体中相应的对应关系,立体中底圆的周长是展开图的弧长,立体中的母线长是展开图中的半径差。
9、正四棱锥是底面为正方形,定点在底面的投影是底面的中心。
10、求经过几何体表面积最短路径实际上是求展开图的最短距离。
11、内切和外接要注意截面图中的几何关系。
12、台体要注意高和斜高的区别,高是几何体的高线,斜高是面上的高线。
单选题
1、下列几何体是棱台的是( )
2、一个等腰三角形绕它的底边所在直线旋转360°形成的曲面所围成的几何体是( )
A.球体
B.圆柱
C.圆台
D.两个共底面的圆锥的组合体
3、如图是四边形ABCD的水平放置的直观图A′B′C′D′,则原四边形ABCD的面积是( )
A.14 B.10
C.28 D.14
4、侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是( )
A.a2 B.a2
C.a2 D.a2
5、如图是一个几何体的三视图,其中主视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( )
A. B.
C. D.
6、一平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.π B.4π
C.4π D.6π
7、若用长为4,宽为2的矩形作侧面围成一个圆柱,则此圆柱轴截面的面积为( )
A.8 B.
C. D.
8、设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的体积为( )
A.3πa3 B.πa3
C.2πa3 D.2πa3
多选题
9、两平行平面截半径为5的球,若截面的面积分别为9π和16π,则这两个平面间的距离可能是( )
A.1 B.3
C.4 D.7
10、已知一个正方形的直观图是如图所示的一个平行四边形,直观图中有一边长为4,则此正方形的面积可能是( )
A.16 B.64
C.8 D.32
11、圆台的上、下底面半径分别是10和20,它的侧面展开图扇环的圆心角为180°,则圆台的( )
A.母线长是20 B.表面积是1100π
C.高是10 D.体积是
12、正四棱锥P-ABCD的底面边长为2,外接球的表面积为24π,则正四棱锥P-ABCD的高可能是( )
A.3+ B.3-
C.2+ D.-2
填空题
13、给出下列说法:①圆柱的底面是圆面;②经过圆柱任意两条母线的截面是一个矩形面;③圆台的任意两条母线的延长线可能相交,也可能不相交;④夹在圆柱的两个截面间的几何体还是一个旋转体;⑤过球面上任意两点只能作一个以球心为圆心的圆.其中说法正确的是________(填序号).
14、如图所示,矩形O′A′B′C′是水平放置的平面图形OABC的斜二测直观图,其中O′A′=6 cm,C′D′=2 cm,则四边形OABC的形状是________.
15、在正三棱柱ABC-A1B1C1中,D为棱AA1的中点,若△BC1D是面积为6的直角三角形,则此三棱柱的体积为________.
16、长方体AC1的长、宽、高分别为3,2,1,从A到C1沿长方体的表面的最短距离为________.
四、解答题
17、已知一个三棱台的上、下底面分别是边长为20 cm和30 cm的正三角形,侧面是全等的等腰梯形,且侧面面积等于上、下底面面积之和,求棱台的高和体积.
18、如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
19、养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高为4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(仓库底面不用建);
(3)哪个方案更经济些?
20、有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
21、若一个底面边长为,侧棱长为的正六棱柱的所有顶点都在一个球面上,求该球的体积和表面积.
参考答案
单选题
1、下列几何体是棱台的是( )
答案 D
解析 A,C都不是由棱锥截成的,不符合棱台的定义,故A,C不满足题意;B中的截面不平行于底面,不符合棱台的定义,故B不满足题意;D符合棱台的定义.故选D.
2、一个等腰三角形绕它的底边所在直线旋转360°形成的曲面所围成的几何体是( )
A.球体
B.圆柱
C.圆台
D.两个共底面的圆锥的组合体
答案 D
解析 过等腰三角形的顶点向底边作垂线,得到两个有一条公共边的全等直角三角形,而直角三角形以一条直角边为轴旋转一周得到的几何体是圆锥.故选D.
3、如图是四边形ABCD的水平放置的直观图A′B′C′D′,则原四边形ABCD的面积是( )
A.14 B.10
C.28 D.14
答案 C
解析 如图,将直观图还原为平面图.∵A′D′∥y′轴,A′B′∥C′D′∥x′轴,A′B′≠C′D′,
∴原图形是一个直角梯形.又D′C′=2,A′B′=5,A′D′=4,∴原直角梯形的上、下底及高分别是2,5,8,故其面积为S=×(2+5)×8=28.
4、侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是( )
A.a2 B.a2
C.a2 D.a2
答案 A
解析 因为底面边长为a,侧面都是等腰直角三角形,所以斜高为,故S侧=3×a×=a2,而S底=a2,故S表=a2.
5、如图是一个几何体的三视图,其中主视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( )
A. B.
C. D.
[答案] B
[解析] 由三视图,可知给定的几何体是一个圆锥的一半,故所求的体积为
××π×12×=.
6、一平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.π B.4π
C.4π D.6π
[答案] B
[解析]
如图,设截面圆的圆心为O′,M为截面圆上任一点,则OO′=,O′M=1,∴OM==,即球的半径为,∴V=π×()3=4π.
7、若用长为4,宽为2的矩形作侧面围成一个圆柱,则此圆柱轴截面的面积为( )
A.8 B.
C. D.
答案 B
解析 若4为底面周长,则圆柱的高为2,此时圆柱的底面直径为,其轴截面的面积为;若底面周长为2,则圆柱的高为4,此时圆柱的底面直径为,其轴截面的面积也为.故选B.
8、设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的体积为( )
A.3πa3 B.πa3
C.2πa3 D.2πa3
[答案] B
[解析] 作出图形的轴截面如图所示,点O即为该球的球心,线段AB即为长方体底面的对角线,
长度为=a,线段BC即为长方体的高,长度为a,线段AC即为长方体的体对角线,长度为=a,则球的半径R==a,所以球的体积V=πR3=πa3.
二、多选题
9、两平行平面截半径为5的球,若截面的面积分别为9π和16π,则这两个平面间的距离可能是( )
A.1 B.3
C.4 D.7
答案 AD
解析 如图(1)所示,若两个平行平面在球心同侧,则CD=-=1.如图(2)所示,若两个平行平面在球心两侧,则CD=+=7.故选AD.
易错点:容易忽略球的对称性,从而漏解。
10、已知一个正方形的直观图是如图所示的一个平行四边形,直观图中有一边长为4,则此正方形的面积可能是( )
A.16 B.64
C.8 D.32
答案 AB
解析 直观图中一条边长为4,此边可能在x′轴上,也可能在y′轴上.若在x′轴上,则原正方形的边长为4,面积为16;若在y′轴上,则原正方形的边长为8,面积为64.故选AB.
11、圆台的上、下底面半径分别是10和20,它的侧面展开图扇环的圆心角为180°,则圆台的( )
A.母线长是20 B.表面积是1100π
C.高是10 D.体积是
答案 ABD
解析 如图所示,设圆台的上底面周长为C,因为扇环的圆心角为180°,
所以C=π·SA,又C=10×2π,所以SA=20,同理SB=40,故圆台的母线AB=SB-SA=20,高h==10,体积V=π×10×(102+10×20+202)=,表面积S=π(10+20)×20+100π+400π=1100π,故选ABD.
12、正四棱锥P-ABCD的底面边长为2,外接球的表面积为24π,则正四棱锥P-ABCD的高可能是( )
A.3+ B.3-
C.2+ D.-2
答案 CD
解析 设四棱锥的高为h,外接球的半径为R,由4πR2=24π,得R=.如图1所示,OH2+HC2=OC2,即(h-)2+2=6,得h=2+.如图2所示,OH2+HC2=OC2,即(-h)2+2=6,得h=-2.
填空题
13、给出下列说法:①圆柱的底面是圆面;②经过圆柱任意两条母线的截面是一个矩形面;③圆台的任意两条母线的延长线可能相交,也可能不相交;④夹在圆柱的两个截面间的几何体还是一个旋转体;⑤过球面上任意两点只能作一个以球心为圆心的圆.其中说法正确的是________(填序号).
答案 ①②
解析 ①正确,圆柱的底面是圆面;②正确,经过圆柱任意两条母线的截面是一个矩形面;③不正确,圆台的母线的延长线一定相交于一点;④不正确,夹在圆柱的两个平行于底面的截面间的几何体才是旋转体;⑤不正确,当这两点是球的直径的两端点时,可以作无数个以球心为圆心的圆.
14、如图所示,矩形O′A′B′C′是水平放置的平面图形OABC的斜二测直观图,其中O′A′=6 cm,C′D′=2 cm,则四边形OABC的形状是________.
答案 菱形
解析 如图,在四边形OABC中,有BC=OA=O′A′=6 cm,AB=OC,OD=2O′D′=2×2=4 cm,CD=C′D′=2 cm,
∴OC= = =6 cm,
∴OA=OC,故四边形OABC是菱形.
15、在正三棱柱ABC-A1B1C1中,D为棱AA1的中点,若△BC1D是面积为6的直角三角形,则此三棱柱的体积为________.
[答案] 8
[解析] 设AC=a,CC1=b,则BD=C1D=,BC1=,又△BC1D是直角三角形,所以2=a2+b2,得b2=2a2,所以BD=C1D=a,又S△BDC1=BD·C1D=×a2=6,所以a2=8,b=4,所以此三棱柱的体积V=a2b=×8×4=8.
16、长方体AC1的长、宽、高分别为3,2,1,从A到C1沿长方体的表面的最短距离为________.
答案 3
解析 如图,在长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1.如图(1)所示,将侧面ABB1A1和侧面BCC1B1展开,则有AC1==,即经过侧面ABB1A1和侧面BCC1B1时的最短距离是;
如图(2)所示,将侧面ABB1A1和底面A1B1C1D1展开,则有AC1==3,即经过侧面ABB1A1和底面A1B1C1D1时的最短距离是3;
如图(3)所示,将侧面ADD1A1和底面A1B1C1D1展开,则有AC1==2,即经过侧面ADD1A1和底面A1B1C1D1时的最短距离是2.因为3<2<,所以从A到C1沿长方体表面的最短距离为3.
四、解答题
17、已知一个三棱台的上、下底面分别是边长为20 cm和30 cm的正三角形,侧面是全等的等腰梯形,且侧面面积等于上、下底面面积之和,求棱台的高和体积.
解 如图所示,在三棱台ABC-A′B′C′中,O′,O分别为上、下底面的中心,D,D′分别是BC,B′C′的中点,连接OO′,A′D′,AD,DD′,则DD′是等腰梯形BCC′B′的高,记为h0,所以
S侧=3××(20+30)h0=75h0.
上、下底面面积之和为S上+S下=×(202+302)=325(cm2).
由S侧=S上+S下,得75h0=325,
所以h0=(cm).
又O′D′=××20=(cm),OD=××30=5(cm),
记棱台的高为h,则h=O′O=
= =4(cm),
由棱台的体积公式,可得棱台的体积
V=(S上+S下+)
=×=1900(cm3).
18、如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
解 将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图,线段AA1的长为所求△AEF周长的最小值.
∵∠AVB=∠A1VC=∠BVC=30°,∴∠AVA1=90°.
又VA=VA1=4,∴AA1=4.∴△AEF周长的最小值为4.
19、养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高为4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(仓库底面不用建);
(3)哪个方案更经济些?
解 (1)如果按方案一,仓库的底面直径变成16 m,
则仓库的体积V1=Sh=×π××4= m3.
如果按方案二,仓库的高变成8 m,
则仓库的体积V2=Sh=×π××8=96π m3.
(2)如果按方案一,仓库的底面直径变成16 m,半径为8 m.
圆锥的母线长l==4 m,
则仓库的表面积S1=π×8×4=32π m2.
如果按方案二,仓库的高变成8 m,
圆锥的母线长为l==10 m,
则仓库的表面积S2=π×6×10=60π m2.
(3)∵V2>V1,S220、有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
解 由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面.
根据切线的性质知,当球在容器内时,水深CP为3r,水面的半径AC为r,则容器内水的体积为
V=V圆锥-V球=π·(r)2·3r-πr3=πr3,
而将球取出后,设容器内水的深度为h,则水面圆的半径为h,
从而容器内水的体积是V′=π··h=πh3,
由V=V′,得h=r.即容器中水的深度为r.
21、若一个底面边长为,侧棱长为的正六棱柱的所有顶点都在一个球面上,求该球的体积和表面积.
解 如图,在底面正六边形ABCDEF中,连接BE,AD交于点O,
连接BE1,
则BE=2OE=2DE,所以BE=,
在Rt△BEE1中,
BE1==2,
所以2R=2,则R=,
所以球的体积V球=πR3=4π,
球的表面积S球=4πR2=12π.
知识点:1、棱台是各条侧棱延长会汇聚到一点。
2、圆锥是直角三角形的一条直角边为轴,另一条直角边为底圆半径旋转而得到。
3、斜二测画法在在直观图里成45度,表示直角坐标系成90度。
4、三视图有两个三角形表示是个椎体,另外俯视图为半圆,表示是底面是圆。
5、过球的截面是个圆形。
6、通过圆锥或者是圆锥的轴截面是轴垂直于底面的平面。
7、长方体或者是正方体的对角线是球的直径。
8、圆锥的展开图和立体中相应的对应关系,立体中底圆的周长是展开图的弧长,立体中的母线长是展开图中的半径差。
9、正四棱锥是底面为正方形,定点在底面的投影是底面的中心。
10、求经过几何体表面积最短路径实际上是求展开图的最短距离。
11、内切和外接要注意截面图中的几何关系。
12、台体要注意高和斜高的区别,高是几何体的高线,斜高是面上的高线。
单选题
1、下列几何体是棱台的是( )
2、一个等腰三角形绕它的底边所在直线旋转360°形成的曲面所围成的几何体是( )
A.球体
B.圆柱
C.圆台
D.两个共底面的圆锥的组合体
3、如图是四边形ABCD的水平放置的直观图A′B′C′D′,则原四边形ABCD的面积是( )
A.14 B.10
C.28 D.14
4、侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是( )
A.a2 B.a2
C.a2 D.a2
5、如图是一个几何体的三视图,其中主视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( )
A. B.
C. D.
6、一平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.π B.4π
C.4π D.6π
7、若用长为4,宽为2的矩形作侧面围成一个圆柱,则此圆柱轴截面的面积为( )
A.8 B.
C. D.
8、设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的体积为( )
A.3πa3 B.πa3
C.2πa3 D.2πa3
多选题
9、两平行平面截半径为5的球,若截面的面积分别为9π和16π,则这两个平面间的距离可能是( )
A.1 B.3
C.4 D.7
10、已知一个正方形的直观图是如图所示的一个平行四边形,直观图中有一边长为4,则此正方形的面积可能是( )
A.16 B.64
C.8 D.32
11、圆台的上、下底面半径分别是10和20,它的侧面展开图扇环的圆心角为180°,则圆台的( )
A.母线长是20 B.表面积是1100π
C.高是10 D.体积是
12、正四棱锥P-ABCD的底面边长为2,外接球的表面积为24π,则正四棱锥P-ABCD的高可能是( )
A.3+ B.3-
C.2+ D.-2
填空题
13、给出下列说法:①圆柱的底面是圆面;②经过圆柱任意两条母线的截面是一个矩形面;③圆台的任意两条母线的延长线可能相交,也可能不相交;④夹在圆柱的两个截面间的几何体还是一个旋转体;⑤过球面上任意两点只能作一个以球心为圆心的圆.其中说法正确的是________(填序号).
14、如图所示,矩形O′A′B′C′是水平放置的平面图形OABC的斜二测直观图,其中O′A′=6 cm,C′D′=2 cm,则四边形OABC的形状是________.
15、在正三棱柱ABC-A1B1C1中,D为棱AA1的中点,若△BC1D是面积为6的直角三角形,则此三棱柱的体积为________.
16、长方体AC1的长、宽、高分别为3,2,1,从A到C1沿长方体的表面的最短距离为________.
四、解答题
17、已知一个三棱台的上、下底面分别是边长为20 cm和30 cm的正三角形,侧面是全等的等腰梯形,且侧面面积等于上、下底面面积之和,求棱台的高和体积.
18、如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
19、养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高为4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(仓库底面不用建);
(3)哪个方案更经济些?
20、有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.
21、若一个底面边长为,侧棱长为的正六棱柱的所有顶点都在一个球面上,求该球的体积和表面积.
参考答案
单选题
1、下列几何体是棱台的是( )
答案 D
解析 A,C都不是由棱锥截成的,不符合棱台的定义,故A,C不满足题意;B中的截面不平行于底面,不符合棱台的定义,故B不满足题意;D符合棱台的定义.故选D.
2、一个等腰三角形绕它的底边所在直线旋转360°形成的曲面所围成的几何体是( )
A.球体
B.圆柱
C.圆台
D.两个共底面的圆锥的组合体
答案 D
解析 过等腰三角形的顶点向底边作垂线,得到两个有一条公共边的全等直角三角形,而直角三角形以一条直角边为轴旋转一周得到的几何体是圆锥.故选D.
3、如图是四边形ABCD的水平放置的直观图A′B′C′D′,则原四边形ABCD的面积是( )
A.14 B.10
C.28 D.14
答案 C
解析 如图,将直观图还原为平面图.∵A′D′∥y′轴,A′B′∥C′D′∥x′轴,A′B′≠C′D′,
∴原图形是一个直角梯形.又D′C′=2,A′B′=5,A′D′=4,∴原直角梯形的上、下底及高分别是2,5,8,故其面积为S=×(2+5)×8=28.
4、侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是( )
A.a2 B.a2
C.a2 D.a2
答案 A
解析 因为底面边长为a,侧面都是等腰直角三角形,所以斜高为,故S侧=3×a×=a2,而S底=a2,故S表=a2.
5、如图是一个几何体的三视图,其中主视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是( )
A. B.
C. D.
[答案] B
[解析] 由三视图,可知给定的几何体是一个圆锥的一半,故所求的体积为
××π×12×=.
6、一平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
A.π B.4π
C.4π D.6π
[答案] B
[解析]
如图,设截面圆的圆心为O′,M为截面圆上任一点,则OO′=,O′M=1,∴OM==,即球的半径为,∴V=π×()3=4π.
7、若用长为4,宽为2的矩形作侧面围成一个圆柱,则此圆柱轴截面的面积为( )
A.8 B.
C. D.
答案 B
解析 若4为底面周长,则圆柱的高为2,此时圆柱的底面直径为,其轴截面的面积为;若底面周长为2,则圆柱的高为4,此时圆柱的底面直径为,其轴截面的面积也为.故选B.
8、设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的体积为( )
A.3πa3 B.πa3
C.2πa3 D.2πa3
[答案] B
[解析] 作出图形的轴截面如图所示,点O即为该球的球心,线段AB即为长方体底面的对角线,
长度为=a,线段BC即为长方体的高,长度为a,线段AC即为长方体的体对角线,长度为=a,则球的半径R==a,所以球的体积V=πR3=πa3.
二、多选题
9、两平行平面截半径为5的球,若截面的面积分别为9π和16π,则这两个平面间的距离可能是( )
A.1 B.3
C.4 D.7
答案 AD
解析 如图(1)所示,若两个平行平面在球心同侧,则CD=-=1.如图(2)所示,若两个平行平面在球心两侧,则CD=+=7.故选AD.
易错点:容易忽略球的对称性,从而漏解。
10、已知一个正方形的直观图是如图所示的一个平行四边形,直观图中有一边长为4,则此正方形的面积可能是( )
A.16 B.64
C.8 D.32
答案 AB
解析 直观图中一条边长为4,此边可能在x′轴上,也可能在y′轴上.若在x′轴上,则原正方形的边长为4,面积为16;若在y′轴上,则原正方形的边长为8,面积为64.故选AB.
11、圆台的上、下底面半径分别是10和20,它的侧面展开图扇环的圆心角为180°,则圆台的( )
A.母线长是20 B.表面积是1100π
C.高是10 D.体积是
答案 ABD
解析 如图所示,设圆台的上底面周长为C,因为扇环的圆心角为180°,
所以C=π·SA,又C=10×2π,所以SA=20,同理SB=40,故圆台的母线AB=SB-SA=20,高h==10,体积V=π×10×(102+10×20+202)=,表面积S=π(10+20)×20+100π+400π=1100π,故选ABD.
12、正四棱锥P-ABCD的底面边长为2,外接球的表面积为24π,则正四棱锥P-ABCD的高可能是( )
A.3+ B.3-
C.2+ D.-2
答案 CD
解析 设四棱锥的高为h,外接球的半径为R,由4πR2=24π,得R=.如图1所示,OH2+HC2=OC2,即(h-)2+2=6,得h=2+.如图2所示,OH2+HC2=OC2,即(-h)2+2=6,得h=-2.
填空题
13、给出下列说法:①圆柱的底面是圆面;②经过圆柱任意两条母线的截面是一个矩形面;③圆台的任意两条母线的延长线可能相交,也可能不相交;④夹在圆柱的两个截面间的几何体还是一个旋转体;⑤过球面上任意两点只能作一个以球心为圆心的圆.其中说法正确的是________(填序号).
答案 ①②
解析 ①正确,圆柱的底面是圆面;②正确,经过圆柱任意两条母线的截面是一个矩形面;③不正确,圆台的母线的延长线一定相交于一点;④不正确,夹在圆柱的两个平行于底面的截面间的几何体才是旋转体;⑤不正确,当这两点是球的直径的两端点时,可以作无数个以球心为圆心的圆.
14、如图所示,矩形O′A′B′C′是水平放置的平面图形OABC的斜二测直观图,其中O′A′=6 cm,C′D′=2 cm,则四边形OABC的形状是________.
答案 菱形
解析 如图,在四边形OABC中,有BC=OA=O′A′=6 cm,AB=OC,OD=2O′D′=2×2=4 cm,CD=C′D′=2 cm,
∴OC= = =6 cm,
∴OA=OC,故四边形OABC是菱形.
15、在正三棱柱ABC-A1B1C1中,D为棱AA1的中点,若△BC1D是面积为6的直角三角形,则此三棱柱的体积为________.
[答案] 8
[解析] 设AC=a,CC1=b,则BD=C1D=,BC1=,又△BC1D是直角三角形,所以2=a2+b2,得b2=2a2,所以BD=C1D=a,又S△BDC1=BD·C1D=×a2=6,所以a2=8,b=4,所以此三棱柱的体积V=a2b=×8×4=8.
16、长方体AC1的长、宽、高分别为3,2,1,从A到C1沿长方体的表面的最短距离为________.
答案 3
解析 如图,在长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1.如图(1)所示,将侧面ABB1A1和侧面BCC1B1展开,则有AC1==,即经过侧面ABB1A1和侧面BCC1B1时的最短距离是;
如图(2)所示,将侧面ABB1A1和底面A1B1C1D1展开,则有AC1==3,即经过侧面ABB1A1和底面A1B1C1D1时的最短距离是3;
如图(3)所示,将侧面ADD1A1和底面A1B1C1D1展开,则有AC1==2,即经过侧面ADD1A1和底面A1B1C1D1时的最短距离是2.因为3<2<,所以从A到C1沿长方体表面的最短距离为3.
四、解答题
17、已知一个三棱台的上、下底面分别是边长为20 cm和30 cm的正三角形,侧面是全等的等腰梯形,且侧面面积等于上、下底面面积之和,求棱台的高和体积.
解 如图所示,在三棱台ABC-A′B′C′中,O′,O分别为上、下底面的中心,D,D′分别是BC,B′C′的中点,连接OO′,A′D′,AD,DD′,则DD′是等腰梯形BCC′B′的高,记为h0,所以
S侧=3××(20+30)h0=75h0.
上、下底面面积之和为S上+S下=×(202+302)=325(cm2).
由S侧=S上+S下,得75h0=325,
所以h0=(cm).
又O′D′=××20=(cm),OD=××30=5(cm),
记棱台的高为h,则h=O′O=
= =4(cm),
由棱台的体积公式,可得棱台的体积
V=(S上+S下+)
=×=1900(cm3).
18、如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
解 将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图,线段AA1的长为所求△AEF周长的最小值.
∵∠AVB=∠A1VC=∠BVC=30°,∴∠AVA1=90°.
又VA=VA1=4,∴AA1=4.∴△AEF周长的最小值为4.
19、养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高为4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积(仓库底面不用建);
(3)哪个方案更经济些?
解 (1)如果按方案一,仓库的底面直径变成16 m,
则仓库的体积V1=Sh=×π××4= m3.
如果按方案二,仓库的高变成8 m,
则仓库的体积V2=Sh=×π××8=96π m3.
(2)如果按方案一,仓库的底面直径变成16 m,半径为8 m.
圆锥的母线长l==4 m,
则仓库的表面积S1=π×8×4=32π m2.
如果按方案二,仓库的高变成8 m,
圆锥的母线长为l==10 m,
则仓库的表面积S2=π×6×10=60π m2.
(3)∵V2>V1,S2
解 由题意知,圆锥的轴截面为正三角形,如图所示为圆锥的轴截面.
根据切线的性质知,当球在容器内时,水深CP为3r,水面的半径AC为r,则容器内水的体积为
V=V圆锥-V球=π·(r)2·3r-πr3=πr3,
而将球取出后,设容器内水的深度为h,则水面圆的半径为h,
从而容器内水的体积是V′=π··h=πh3,
由V=V′,得h=r.即容器中水的深度为r.
21、若一个底面边长为,侧棱长为的正六棱柱的所有顶点都在一个球面上,求该球的体积和表面积.
解 如图,在底面正六边形ABCDEF中,连接BE,AD交于点O,
连接BE1,
则BE=2OE=2DE,所以BE=,
在Rt△BEE1中,
BE1==2,
所以2R=2,则R=,
所以球的体积V球=πR3=4π,
球的表面积S球=4πR2=12π.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
