20.1.2第1课时 中位数和众数 课件(共29页)
文档属性
| 名称 | 20.1.2第1课时 中位数和众数 课件(共29页) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
人教版八下数学
精品同步教学课件
20.1 数据的集中趋势
20.1.2第1课时 中位数和众数
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
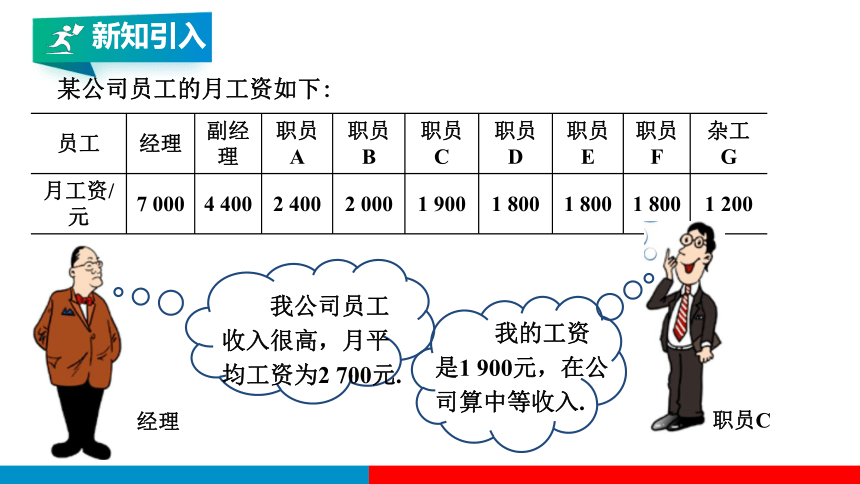
某公司员工的月工资如下:
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7 000 4 400 2 400 2 000 1 900 1 800 1 800 1 800 1 200
我公司员工收入很高,月平均工资为2 700元.
我的工资是1 900元,在公司算中等收入.
经理
职员C
新知引入
应聘者
你怎样看待该公司员工的收入
职员D
这个公司员工收入到底怎样呢?
我们好几个人工资都是1 800元.
新知引入
中 位 数
1
定义:将一组数据按照由小到大(或由大到小)的
顺序排列,如果数据的个数是奇数,则称处于中
间位置的数为这组数据的中位数;如果数据的个
数是偶数,则称中间两个数据的平均数为这组数
据的中位数.
自主学习
2.求中位数的步骤:
(1)将数据由小到大(或由大到小)排列;
(2)数清数据个数是奇数还是偶数,如果数据个数
为奇数,则取中间的数作为中位数;如果数据
个数为偶数,则取中间两数的平均数作为中位
数.
自主学习
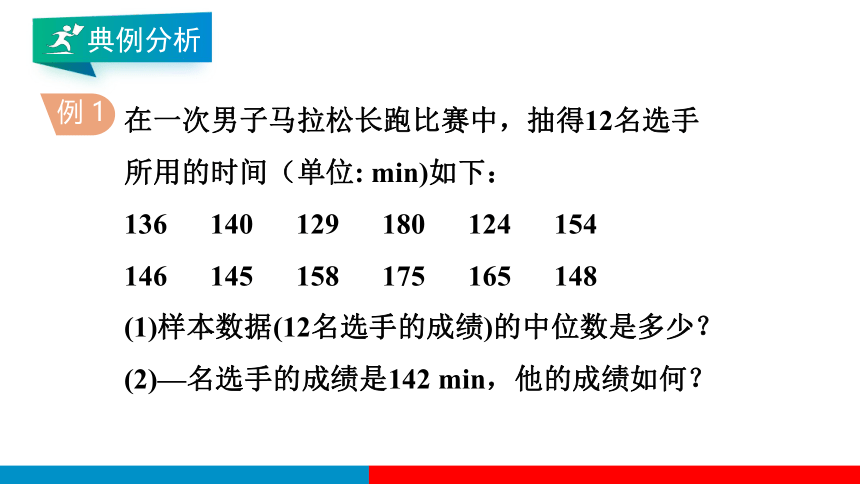
例 1
在一次男子马拉松长跑比赛中,抽得12名选手
所用的时间(单位: min)如下:
136 140 129 180 124 154
146 145 158 175 165 148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)—名选手的成绩是142 min,他的成绩如何?
典例分析
124 129 136 140 145 146
148 154 158 165 175 180
解:
(1)先将样本数据按照由小到大的顺序排列:
这组数据的中位数为处于中间的两个数146,
148的平均数,即
因此样本数据的中位数是147.
典例分析
(2) 根据(1)中得到的样本数据的中位数, 可以估
计,在这次马拉松比赛中,大约有一半选手
的成绩快于147 min,有一半选手的成绩慢于
147 min. 这名选手的成绩是142 min,快于中
位数147 min,可以推测他的成绩比一半以上
选手的成绩好.
典例分析
例2
某班七个合作学习小组人数如下:4,5,5,x,6,7,8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.5 B.5.5 C.6 D.7
根据平均数的定义得,4+5+5+x+6+7+8=
6×7,解得x=7.从小到大排列这组数据为4,5,
5,6,7,7,8,所以中位数是6.
C
导引:
典例分析
归 纳
求一组数据的中位数的方法:
先将数据按照从小到大(或从大到小)的顺序进行
排列,然后根据数据的个数确定中位数,如果数据
的个数是奇数,则处于中间位置的数为中位数;如
果数据的个数是偶数,则中间两个数据的平均数为
中位数,注意,中位数不一定是这组数据中的数.
自主学习
1.
下面的条形图描述了某车间工人日加工零件数
的情况.请找出这些工
人日加工零件数的中
位数,并说明这个中
位数的意义.
解:
因为这组数据的中位数为处于中间的两个数据6,6的平均数,所以这些工人日加工零件的中位数是6. 意义略.
课堂练习
2.
【中考·黄冈】某校10名篮球运动员的年龄情况,统计如下表:
则这10名篮球运动员年龄的中位数为( )
A.12 B.13
C.13.5 D.14
年龄(岁) 12 13 14 15
人数(名) 2 4 3 1
B
课堂练习
3.
【中考·福州】若一组数据1,2,3,4,x的平均数与中位数相同,则实数x的值不可能是( )
A.0 B.2.5
C.3 D.5
C
课堂练习
4.
【中考·镇江】根据下表中的信息解决问题:
若该组数据的中位数不大于38,则符合条件的正整数a的取值共有( )
A.3个 B.4个
C.5个 D.6个
数据 37 38 39 40 41
频数 8 4 5 a 1
C
课堂练习
众 数
2
某商店有200L,215L,185L,180L四种型号
的冰箱,一段时间内共销售58台,其中四个型号分
别售6台,30台,14台,8台,在研究电冰箱出售情
况时,商店经理关心这组数据的平均数吗?他关心
的是什么?
自主学习
销售量的多少是商店经理最关心的一个问题,
因此在这个问题中平均数不再是考察的主要对象,这组数据的中出现最多的数是215L ,说明这种型号的电冰箱销量最好,这才是商店经理最为关心的.
商店经理关心的数215L在这组数据中出现的次数
最多,我们把他关心的叫众数,也就是哪种型号的电
冰箱销量最好.
1.定义:一组数据中出现次数最多的那个数据叫做这组数
据的众数.
2.要点精析:
(1)一组数据的众数一定出现在这组数据中;
(2)一组数据的众数可能不止一个;
(3)一组数据也可能没有众数;因为有可能数据出现的频
数相同;
(4)众数可以在某种意义上代表这组数据的整体情况.
自主学习
例 3
一家鞋店在一段时间内销售了某种女鞋30双,各
种尺码鞋的销售量如表所示. 你能根据表中的数
据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
典例分析
由表可以看出,在鞋的尺码组成的数据中,
23.5是这组数据的众数,即23. 5 cm的鞋销售
量最大. 因此可以建议鞋店多进23.5 cm的鞋.
解:
典例分析
每年的4月23日是“世界读书日”. 某中学为了了解
八年级学生的读书情况,随机调查了50名学生的读
书册数,统计数据如下表:
则这50名学生读书册数的众数、中位数分别是( )
A.3,3 B.3,2 C.2,3 D.2,2
册数 0 1 2 3 4
人数 3 13 16 17 1
B
例4
典例分析
∵在这组样本数据中,3出现了17次,出现的
次数最多,
∴这组数据的众数是3.
∵将这组样本数据按从小到大的顺序排列后,处于中间的两个数都是2,
∴这组数据的中位数为2.
导引:
典例分析
归 纳
求一组数据的众数的方法:找一组数据的众数,
可用观察法;当不易观察时,可用列表的形式把各数
据出现的次数全部计算出来,即可得出众数.
自主学习
1.
【中考·成都】学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:
则得分的众数和中位数分别为( )
A.70分,70分 B.80分,80分
C.70分,80分 D.80分,70分
得分(分) 60 70 80 90 100
人数(人) 7 12 10 8 3
C
课堂练习
2.
【中考·安顺】如图是根据某班40名同学一周的
体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16,10.5
B.8,9
C.16,8.5
D.8,8.5
B
课堂练习
中位数和众数
中位数:
1.在计算一组数据的中位数时,其步骤为
(1)将这组数据按从小到大(或从大到小)的顺序排列;
(2)找到处在最中间位置的一个数或最中间的两个数
的平均数即为中位数.
课堂小结
中位数和众数
众数:
1. 若几个数据出现的次数相同,并且比其他数据出
现的次数都多,那么这几个数据都是这组数据的
众数;当所有的数出现的次数一样多时,无众数.
2. 众数是一组数据中的某个或几个数据,其单位与
数据的单位相同.
3. 众数是一组数据中出现次数最多的数,而不是该
数据出现的次数.
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版八下数学
精品同步教学课件
20.1 数据的集中趋势
20.1.2第1课时 中位数和众数
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
某公司员工的月工资如下:
员工 经理 副经理 职员A 职员B 职员C 职员D 职员E 职员F 杂工G
月工资/元 7 000 4 400 2 400 2 000 1 900 1 800 1 800 1 800 1 200
我公司员工收入很高,月平均工资为2 700元.
我的工资是1 900元,在公司算中等收入.
经理
职员C
新知引入
应聘者
你怎样看待该公司员工的收入
职员D
这个公司员工收入到底怎样呢?
我们好几个人工资都是1 800元.
新知引入
中 位 数
1
定义:将一组数据按照由小到大(或由大到小)的
顺序排列,如果数据的个数是奇数,则称处于中
间位置的数为这组数据的中位数;如果数据的个
数是偶数,则称中间两个数据的平均数为这组数
据的中位数.
自主学习
2.求中位数的步骤:
(1)将数据由小到大(或由大到小)排列;
(2)数清数据个数是奇数还是偶数,如果数据个数
为奇数,则取中间的数作为中位数;如果数据
个数为偶数,则取中间两数的平均数作为中位
数.
自主学习
例 1
在一次男子马拉松长跑比赛中,抽得12名选手
所用的时间(单位: min)如下:
136 140 129 180 124 154
146 145 158 175 165 148
(1)样本数据(12名选手的成绩)的中位数是多少?
(2)—名选手的成绩是142 min,他的成绩如何?
典例分析
124 129 136 140 145 146
148 154 158 165 175 180
解:
(1)先将样本数据按照由小到大的顺序排列:
这组数据的中位数为处于中间的两个数146,
148的平均数,即
因此样本数据的中位数是147.
典例分析
(2) 根据(1)中得到的样本数据的中位数, 可以估
计,在这次马拉松比赛中,大约有一半选手
的成绩快于147 min,有一半选手的成绩慢于
147 min. 这名选手的成绩是142 min,快于中
位数147 min,可以推测他的成绩比一半以上
选手的成绩好.
典例分析
例2
某班七个合作学习小组人数如下:4,5,5,x,6,7,8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.5 B.5.5 C.6 D.7
根据平均数的定义得,4+5+5+x+6+7+8=
6×7,解得x=7.从小到大排列这组数据为4,5,
5,6,7,7,8,所以中位数是6.
C
导引:
典例分析
归 纳
求一组数据的中位数的方法:
先将数据按照从小到大(或从大到小)的顺序进行
排列,然后根据数据的个数确定中位数,如果数据
的个数是奇数,则处于中间位置的数为中位数;如
果数据的个数是偶数,则中间两个数据的平均数为
中位数,注意,中位数不一定是这组数据中的数.
自主学习
1.
下面的条形图描述了某车间工人日加工零件数
的情况.请找出这些工
人日加工零件数的中
位数,并说明这个中
位数的意义.
解:
因为这组数据的中位数为处于中间的两个数据6,6的平均数,所以这些工人日加工零件的中位数是6. 意义略.
课堂练习
2.
【中考·黄冈】某校10名篮球运动员的年龄情况,统计如下表:
则这10名篮球运动员年龄的中位数为( )
A.12 B.13
C.13.5 D.14
年龄(岁) 12 13 14 15
人数(名) 2 4 3 1
B
课堂练习
3.
【中考·福州】若一组数据1,2,3,4,x的平均数与中位数相同,则实数x的值不可能是( )
A.0 B.2.5
C.3 D.5
C
课堂练习
4.
【中考·镇江】根据下表中的信息解决问题:
若该组数据的中位数不大于38,则符合条件的正整数a的取值共有( )
A.3个 B.4个
C.5个 D.6个
数据 37 38 39 40 41
频数 8 4 5 a 1
C
课堂练习
众 数
2
某商店有200L,215L,185L,180L四种型号
的冰箱,一段时间内共销售58台,其中四个型号分
别售6台,30台,14台,8台,在研究电冰箱出售情
况时,商店经理关心这组数据的平均数吗?他关心
的是什么?
自主学习
销售量的多少是商店经理最关心的一个问题,
因此在这个问题中平均数不再是考察的主要对象,这组数据的中出现最多的数是215L ,说明这种型号的电冰箱销量最好,这才是商店经理最为关心的.
商店经理关心的数215L在这组数据中出现的次数
最多,我们把他关心的叫众数,也就是哪种型号的电
冰箱销量最好.
1.定义:一组数据中出现次数最多的那个数据叫做这组数
据的众数.
2.要点精析:
(1)一组数据的众数一定出现在这组数据中;
(2)一组数据的众数可能不止一个;
(3)一组数据也可能没有众数;因为有可能数据出现的频
数相同;
(4)众数可以在某种意义上代表这组数据的整体情况.
自主学习
例 3
一家鞋店在一段时间内销售了某种女鞋30双,各
种尺码鞋的销售量如表所示. 你能根据表中的数
据为这家鞋店提供进货建议吗?
尺码/cm 22 22.5 23 23.5 24 24.5 25
销售量/双 1 2 5 11 7 3 1
典例分析
由表可以看出,在鞋的尺码组成的数据中,
23.5是这组数据的众数,即23. 5 cm的鞋销售
量最大. 因此可以建议鞋店多进23.5 cm的鞋.
解:
典例分析
每年的4月23日是“世界读书日”. 某中学为了了解
八年级学生的读书情况,随机调查了50名学生的读
书册数,统计数据如下表:
则这50名学生读书册数的众数、中位数分别是( )
A.3,3 B.3,2 C.2,3 D.2,2
册数 0 1 2 3 4
人数 3 13 16 17 1
B
例4
典例分析
∵在这组样本数据中,3出现了17次,出现的
次数最多,
∴这组数据的众数是3.
∵将这组样本数据按从小到大的顺序排列后,处于中间的两个数都是2,
∴这组数据的中位数为2.
导引:
典例分析
归 纳
求一组数据的众数的方法:找一组数据的众数,
可用观察法;当不易观察时,可用列表的形式把各数
据出现的次数全部计算出来,即可得出众数.
自主学习
1.
【中考·成都】学习全等三角形时,数学兴趣小组设计并组织了“生活中的全等”的比赛,全班同学的比赛结果统计如下表:
则得分的众数和中位数分别为( )
A.70分,70分 B.80分,80分
C.70分,80分 D.80分,70分
得分(分) 60 70 80 90 100
人数(人) 7 12 10 8 3
C
课堂练习
2.
【中考·安顺】如图是根据某班40名同学一周的
体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16,10.5
B.8,9
C.16,8.5
D.8,8.5
B
课堂练习
中位数和众数
中位数:
1.在计算一组数据的中位数时,其步骤为
(1)将这组数据按从小到大(或从大到小)的顺序排列;
(2)找到处在最中间位置的一个数或最中间的两个数
的平均数即为中位数.
课堂小结
中位数和众数
众数:
1. 若几个数据出现的次数相同,并且比其他数据出
现的次数都多,那么这几个数据都是这组数据的
众数;当所有的数出现的次数一样多时,无众数.
2. 众数是一组数据中的某个或几个数据,其单位与
数据的单位相同.
3. 众数是一组数据中出现次数最多的数,而不是该
数据出现的次数.
课堂小结
https://www.21cnjy.com/help/help_extract.php
