20.1.2第2课时 平均数、中位数和众数综合应用 课件(共28页)
文档属性
| 名称 | 20.1.2第2课时 平均数、中位数和众数综合应用 课件(共28页) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 13:12:25 | ||
图片预览







文档简介
(共28张PPT)
人教版八下数学
精品同步教学课件
20.1 数据的集中趋势
20.1.2第2课时平均数、中位数、众数的综合
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
例 1
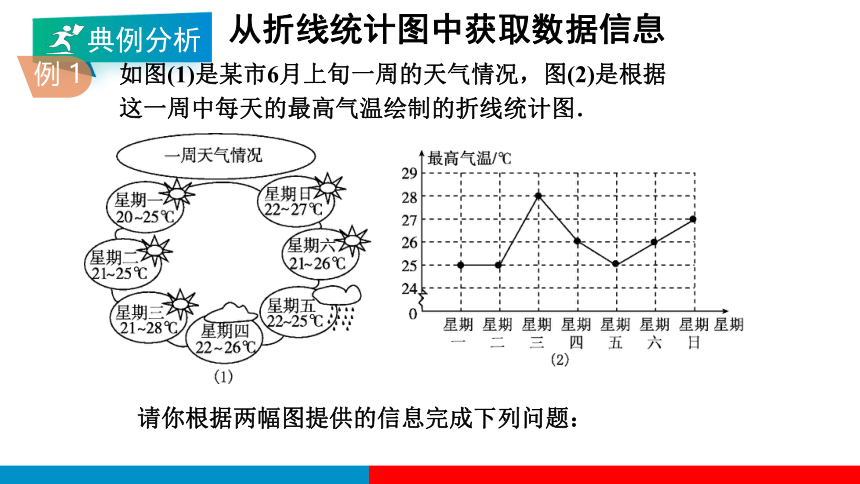
如图(1)是某市6月上旬一周的天气情况,图(2)是根据
这一周中每天的最高气温绘制的折线统计图.
请你根据两幅图提供的信息完成下列问题:
从折线统计图中获取数据信息
典例分析
(1)这一周中温差最大的一天是星期________;
(2)这一周中每天最高气温的众数是______℃,中位数是______℃,
平均数是________℃;
(3)这两幅图各有特点,而关于折线统计图的优点,下列四句话中描
述最贴切的一句是________.(填序号)
①可以清楚地告诉我们每天天气情况;②可以清楚地告诉我们各
部分数量占总量的百分比的情况;③可以直观地告诉我们这一周
每天最高气温的变化情况;④可以清楚地告诉我们这一周每天气
温的总体情况.
三
25
26
③
典例分析
归纳:折线统计图具有能够显示数据的变化趋势,反映事物的变化情况的特点,所以利用折线统计图比较容易看出数据的众数,也比较容易求出数据的中位数和平均数.
典例分析
1.
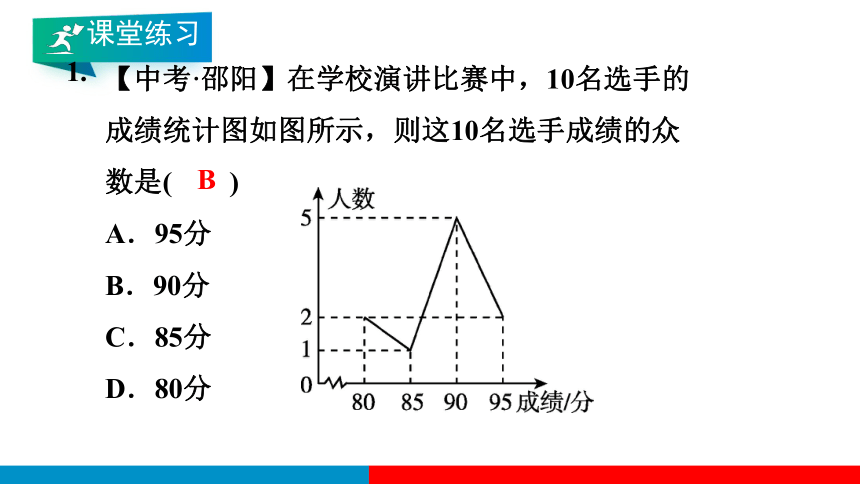
【中考·邵阳】在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
A.95分
B.90分
C.85分
D.80分
B
课堂练习
2.
端午节期间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的中位数是( )
A.22
B.24
C.25
D.27
B
课堂练习
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄
情况如图.
(1)观察图,你能从图中分别看出三支球队队员年龄的众数吗?
中位数呢?
(2)根据图,你能大致估计出三支球队队员的平均年龄哪个大、
哪个小吗?你是怎么估计的?
(3)计算出三支球队队员的平均年龄,看看你的估计是否准确.
从条形统计图(频数直方图)中获取数据信息
典例分析
因为条形统计图能清楚地表示出数量的多少,
所以利用条形统计图更容易看出数据的众数、中位
数,利用加权平均数的求法可以求出数据的平均数.
典例分析
例2
某商场服装部为了调动营业员的积极性,决定实
行目标管理,根据目标完成的情况对营业员进行
适当的奖励. 为了确定一个适当的月销售目标,
商场服装部统计了每位营业员在某月的销售额
(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
典例分析
月销售额在哪个值的人数最多?中间的月销售
额是多少?平均月销售额是多少?
如果想确定一个较高的销售目标,你认 为月销
售额定为多少合适?说明理由.
如果想让一半左右的营业员都能达到销售目标,
你认为月销售额定为多少合适?说明理由.
典例分析
整理上面的数据得到下表和下图.
解:
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
典例分析
从上表或上图可以看出,样本数据的众数是15,
中位数是 18, 利用计算器求得这组数据的平均
数约是20. 可以推测,这个服装部营业员的月
销售额为15万元的人数最多,中间的月销售额
是18万元,平均月销售额 大约是20万元.
典例分析
如果想确定一个较高的销售目标,这个目标可以
定为每月20万元 (平均数).因为从样本数据看,在
平均数、中位数和众数中,平均数最大. 可以估
计,月销售额定为每月20万元是一个较高目标,
大约会有 的营业员获得奖励.
典例分析
如果想让一半左右的营业员能够达到销售目标,
月销售额可以定为每月18万元(中位数). 因为从
样本情况看,月销售额在18万元以上(含18万
元)的有16人,占总人数的一半左右. 可以估
计,如果月销售额定为18万 元,将有一半左右
的营业员获得奖励.
典例分析
归 纳
选择具有代表一组数据特点的数据的方法:
对于一组数据,当没有极端值时,用平均数作
为这组数据的代表值;当有极端值时,用中位数或
众数作为这组数据的代表值.
典例分析
1.
【中考·宜昌】在6月26日“国际禁毒日”来临之
际,华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )
A.18岁
B.19岁
C.20岁
D.21岁
C
课堂练习
2.
如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),
则捐款人数最多的一组是( )
A.5~10元
B.10~15元
C.15~20元
D.20~25元
C
课堂练习
从扇形统计图获取数据信息
做一做
小明调查了班级里20
名同学本学期计划购买课
外书的花费情况,并将结
果绘制成了右图.
(1)在这20名同学中,本学
期计划购买课外书的花
费的众数是多少?
(2)计算这20名同学计划购买课外书的平均花费.你是怎么计算的
自主学习
想一想
在上面的问题中,如果不知道调查的总人数,
你还能求平均数吗
自主学习
因为扇形统计图能看出部分在总体中所占的百分
比,所以利用扇形统计图更容易看出数据的众数;利
用加权平均数的求法可以求出数据的平均数.
自主学习
某地连续统计了 10天日
最高气温,并绘制成如
图所示的扇形统计图.
(1)这10天中,日最高
气温的众数是多少?
(2)计算这10天日最高
气温的平均值.
解:(1)根据扇形统计图,35℃占的比例最大,因此日平均气温的
众数是35℃;
(2)这10天日最高气温的平均值是:32×10%+33×20%+34×
20%+35×30%+36×20%=34.3(℃).
例 3
典例分析
归 纳
从统计图中我们可以获取有用的数据信息,通过
计算可以得到这组数据的平均数;通过数各个数据出
现的次数可以确定这组数据的众数;中位数是把这组
数据按大小顺序排列后处于最中间位置的一个数据.
典例分析
1.
【中考·泰安】某学校将为七年级学生开设A,B,C,D,E,F共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图所示的统计图和如下统计表(不完整):
选修课 A B C D E F
人数/人 40 60 100
课堂练习
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E,F的人数分
别为80人,70人
D.喜欢选修课C的人数最少
D
课堂练习
比较5月份两组家庭用水量的中位数,下列说法正确的是( )
A.甲组比乙组大
B.甲、乙两组相同
C.乙组比甲组大
D.无法判断
B
课堂练均数、中位数、众数“三数”的综合
三种统计图的优缺点:
(1)因为折线统计图具有能够显示数据的变化趋势,
反映事物的变化情况的特点,所以利用折线统
计图比较容易看出数据的众数,也比较容易求
出数据的中位数和平均数;
课堂小结
平均数、中位数、众数“三数”的综合
(2)因为条形统计图能清楚地表示出数量的多少,所
以利用条形统计图更容易看出数据的众数、中位
数,利用加权平均数的求法可以求出数据的平均
数;
(3)因为扇形统计图能看出部分在总体中所占的百分
比,所以利用扇形统计图更容易看出数据的众数;
利用加权平均数的求法可以求出数据的平均数.
课堂小结
人教版八下数学
精品同步教学课件
20.1 数据的集中趋势
20.1.2第2课时平均数、中位数、众数的综合
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
例 1
如图(1)是某市6月上旬一周的天气情况,图(2)是根据
这一周中每天的最高气温绘制的折线统计图.
请你根据两幅图提供的信息完成下列问题:
从折线统计图中获取数据信息
典例分析
(1)这一周中温差最大的一天是星期________;
(2)这一周中每天最高气温的众数是______℃,中位数是______℃,
平均数是________℃;
(3)这两幅图各有特点,而关于折线统计图的优点,下列四句话中描
述最贴切的一句是________.(填序号)
①可以清楚地告诉我们每天天气情况;②可以清楚地告诉我们各
部分数量占总量的百分比的情况;③可以直观地告诉我们这一周
每天最高气温的变化情况;④可以清楚地告诉我们这一周每天气
温的总体情况.
三
25
26
③
典例分析
归纳:折线统计图具有能够显示数据的变化趋势,反映事物的变化情况的特点,所以利用折线统计图比较容易看出数据的众数,也比较容易求出数据的中位数和平均数.
典例分析
1.
【中考·邵阳】在学校演讲比赛中,10名选手的成绩统计图如图所示,则这10名选手成绩的众数是( )
A.95分
B.90分
C.85分
D.80分
B
课堂练习
2.
端午节期间,某市一周每天最高气温(单位:℃)情况如图所示,则这组表示最高气温数据的中位数是( )
A.22
B.24
C.25
D.27
B
课堂练习
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄
情况如图.
(1)观察图,你能从图中分别看出三支球队队员年龄的众数吗?
中位数呢?
(2)根据图,你能大致估计出三支球队队员的平均年龄哪个大、
哪个小吗?你是怎么估计的?
(3)计算出三支球队队员的平均年龄,看看你的估计是否准确.
从条形统计图(频数直方图)中获取数据信息
典例分析
因为条形统计图能清楚地表示出数量的多少,
所以利用条形统计图更容易看出数据的众数、中位
数,利用加权平均数的求法可以求出数据的平均数.
典例分析
例2
某商场服装部为了调动营业员的积极性,决定实
行目标管理,根据目标完成的情况对营业员进行
适当的奖励. 为了确定一个适当的月销售目标,
商场服装部统计了每位营业员在某月的销售额
(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
典例分析
月销售额在哪个值的人数最多?中间的月销售
额是多少?平均月销售额是多少?
如果想确定一个较高的销售目标,你认 为月销
售额定为多少合适?说明理由.
如果想让一半左右的营业员都能达到销售目标,
你认为月销售额定为多少合适?说明理由.
典例分析
整理上面的数据得到下表和下图.
解:
销售额/万元 13 14 15 16 17 18 19 22 23 24 26 28 30 32
人数 1 1 5 4 3 2 3 1 1 1 2 3 1 2
典例分析
从上表或上图可以看出,样本数据的众数是15,
中位数是 18, 利用计算器求得这组数据的平均
数约是20. 可以推测,这个服装部营业员的月
销售额为15万元的人数最多,中间的月销售额
是18万元,平均月销售额 大约是20万元.
典例分析
如果想确定一个较高的销售目标,这个目标可以
定为每月20万元 (平均数).因为从样本数据看,在
平均数、中位数和众数中,平均数最大. 可以估
计,月销售额定为每月20万元是一个较高目标,
大约会有 的营业员获得奖励.
典例分析
如果想让一半左右的营业员能够达到销售目标,
月销售额可以定为每月18万元(中位数). 因为从
样本情况看,月销售额在18万元以上(含18万
元)的有16人,占总人数的一半左右. 可以估
计,如果月销售额定为18万 元,将有一半左右
的营业员获得奖励.
典例分析
归 纳
选择具有代表一组数据特点的数据的方法:
对于一组数据,当没有极端值时,用平均数作
为这组数据的代表值;当有极端值时,用中位数或
众数作为这组数据的代表值.
典例分析
1.
【中考·宜昌】在6月26日“国际禁毒日”来临之
际,华明中学围绕“珍爱生命,远离毒品”主题,组织师生到当地戒毒所开展相关问题的问卷调查活动,其中“初次吸毒时的年龄”在17至21岁的统计结果如图所示,则这些年龄的众数是( )
A.18岁
B.19岁
C.20岁
D.21岁
C
课堂练习
2.
如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),
则捐款人数最多的一组是( )
A.5~10元
B.10~15元
C.15~20元
D.20~25元
C
课堂练习
从扇形统计图获取数据信息
做一做
小明调查了班级里20
名同学本学期计划购买课
外书的花费情况,并将结
果绘制成了右图.
(1)在这20名同学中,本学
期计划购买课外书的花
费的众数是多少?
(2)计算这20名同学计划购买课外书的平均花费.你是怎么计算的
自主学习
想一想
在上面的问题中,如果不知道调查的总人数,
你还能求平均数吗
自主学习
因为扇形统计图能看出部分在总体中所占的百分
比,所以利用扇形统计图更容易看出数据的众数;利
用加权平均数的求法可以求出数据的平均数.
自主学习
某地连续统计了 10天日
最高气温,并绘制成如
图所示的扇形统计图.
(1)这10天中,日最高
气温的众数是多少?
(2)计算这10天日最高
气温的平均值.
解:(1)根据扇形统计图,35℃占的比例最大,因此日平均气温的
众数是35℃;
(2)这10天日最高气温的平均值是:32×10%+33×20%+34×
20%+35×30%+36×20%=34.3(℃).
例 3
典例分析
归 纳
从统计图中我们可以获取有用的数据信息,通过
计算可以得到这组数据的平均数;通过数各个数据出
现的次数可以确定这组数据的众数;中位数是把这组
数据按大小顺序排列后处于最中间位置的一个数据.
典例分析
1.
【中考·泰安】某学校将为七年级学生开设A,B,C,D,E,F共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图所示的统计图和如下统计表(不完整):
选修课 A B C D E F
人数/人 40 60 100
课堂练习
根据图表提供的信息,下列结论错误的是( )
A.这次被调查的学生人数为400人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中喜欢选修课E,F的人数分
别为80人,70人
D.喜欢选修课C的人数最少
D
课堂练习
比较5月份两组家庭用水量的中位数,下列说法正确的是( )
A.甲组比乙组大
B.甲、乙两组相同
C.乙组比甲组大
D.无法判断
B
课堂练均数、中位数、众数“三数”的综合
三种统计图的优缺点:
(1)因为折线统计图具有能够显示数据的变化趋势,
反映事物的变化情况的特点,所以利用折线统
计图比较容易看出数据的众数,也比较容易求
出数据的中位数和平均数;
课堂小结
平均数、中位数、众数“三数”的综合
(2)因为条形统计图能清楚地表示出数量的多少,所
以利用条形统计图更容易看出数据的众数、中位
数,利用加权平均数的求法可以求出数据的平均
数;
(3)因为扇形统计图能看出部分在总体中所占的百分
比,所以利用扇形统计图更容易看出数据的众数;
利用加权平均数的求法可以求出数据的平均数.
课堂小结
