20.2 数据的波动程度 课件(共33页)
文档属性
| 名称 | 20.2 数据的波动程度 课件(共33页) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 13:08:20 | ||
图片预览










文档简介
(共33张PPT)
人教版八下数学
精品同步教学课件
20.2 数据的波动程度
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
方差及其求法
1
问题 农科院计划为某地选择合适的甜玉米种子.选择
种子时,甜玉米的产量和产量的稳定性是农科院所关
心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10块自然条件相同的试验田进行试验,得
到各试验田每公顷的产量 (单位:t) 如下表所示.
问题引入
根据这些数据估计,农科院应该选择哪种甜玉米种子呢
上面两组数据的平均数分别是
甲 7.65 7.50 7.62 7.59 7.65 7.64 7.50 7.40 7.41 7.41
乙 7.55 7.56 7.53 7.44 7.49 7.52 7.58 7.46 7.53 7.49
说明在试验田中,甲、乙两种甜玉米的平均产量
相差不大.由此可以估计出这个地区种植这两种甜玉米,
它们的平均产量相差不大.
问题引入
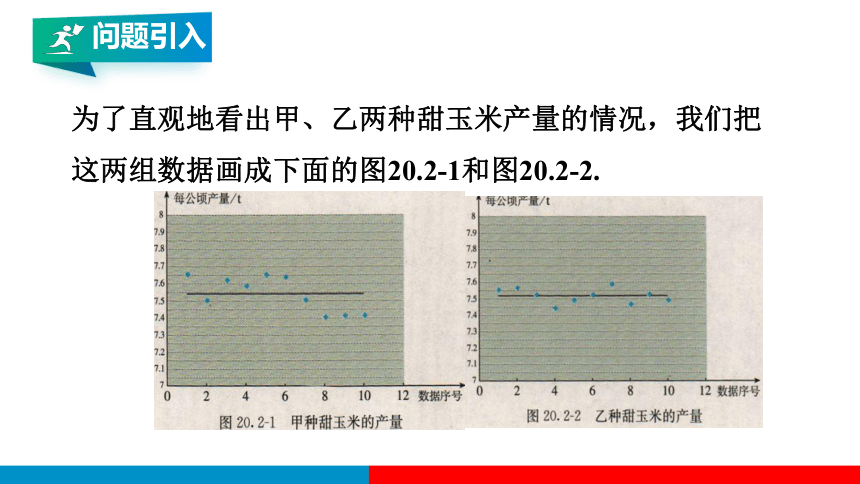
为了直观地看出甲、乙两种甜玉米产量的情况,我们把
这两组数据画成下面的图20.2-1和图20.2-2.
问题引入
比较上面的两幅图可以看出,甲种甜玉米在各
试验田的产量波动较大, 乙 种甜玉米在各试验田的
产量较集中地分布在平均产量附近. 从图中看出的
结果能否用一个量来刻画呢?
问题引入
为了刻画一组数据波动的大小,可以采用很多
方法. 统计中常采用下面的 做法:设有n个数据x1,
x2 ,… ,xn,各数据与它们的平均数 的差的平方
分别是 … ,
我们用这些值的平均数,即用
来衡量这组数据波动的大小,并把它叫做这组数据
的方差,记作s2.
自主学习
例 1
人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:
=80,s2甲=240,s2乙=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
典例分析
在本题中,给出平均分和方差两种数据,那么平
均分要考查的是甲、乙两班的成绩的优劣,而成
绩的稳定性就要看两班成绩的方差了.那么所谓
的稳定性,也就是指成绩的波动.成绩波动越小,
成绩越稳定.根据“方差越大,数据的波动越大:
方差越小,数据的波动越小,我们很容易发现乙
班的方差比甲班的小,所以乙班的成绩较稳定.
分析:
典例分析
归 纳
在利用方差比较两组数据的波动情况时,一定要先
计算两组数据的平均数.一般说来,平均数可能反映数
据的优劣程度,如果在平均数上已经能够区分几组数据
的优劣,那么就不用再考虑方差的大小了.但在实际的
习题中,往往都是平均值相同,那么此时就要考虑数据
的方差情况了.由此可得到:在解决问题时,要先算平
均数,当平均值不同时,择优选取;当平均数相同时,
比较方差,选择波动较小的一组数据.
典例分析
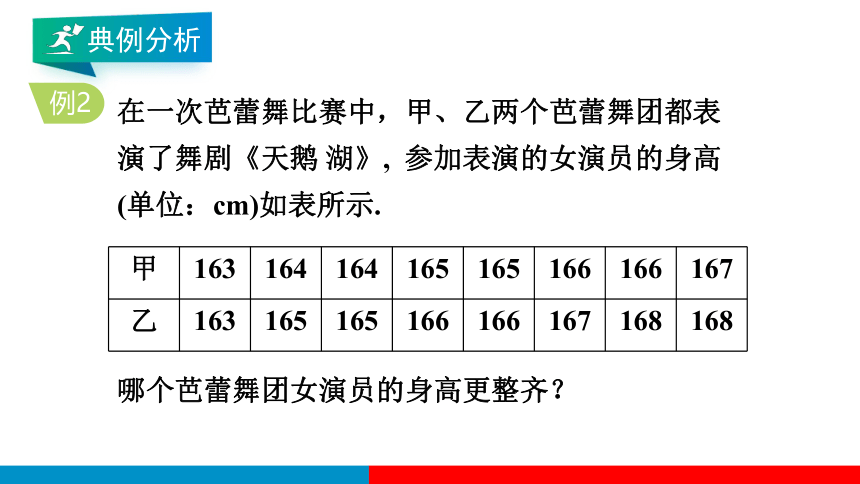
例2
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅 湖》, 参加表演的女演员的身高(单位:cm)如表所示.
哪个芭蕾舞团女演员的身高更整齐?
甲 163 164 164 165 165 166 166 167
乙 163 165 165 166 166 167 168 168
典例分析
甲、乙两团演员的身高平均数分别是
解:
方差分别是
由s甲2 < s乙2 可知,甲芭蕾舞团女演员的身高更整齐.
典例分析
归 纳
一般地,设n个数据x1,x2,…,xn的平均数为
,则方差
s2=
它反映了一组数据的波动大小,方差越大,波动性
越大,反之也成立.
典例分析
1.
【中考·自贡】对于一组统计数据3,3,6,5,
3. 下列说法错误的是( )
A.众数是3 B.平均数是4
C.方差是1.6 D.中位数是6
D
自主学习
2.
设数据x1,x2,…,xn的平均数为x,方差为s2,若s2=0,则( )
A.x=0
B.x1+x2+…+xn=0
C.x1=x2=…=xn=0
D.x1=x2=…=xn
D
自主学习
3.
【中考·通辽】若数据10,9,a,12,9的平均数是10,则这组数据的方差是( )
A.1 B.1.2
C.0.9 D.1.4
B
自主学习
4.
【中考·南京】若一组数据2,3,4,5,x的方
差与另一组数据5,6,7,8,9的方差相等,
则x的值为( )
A.1 B.6
C.1或6 D.5或6
C
自主学习
5.
【中考·遵义】如果一组数据x1,x2,…,xn的
方差是4,则另一组数据x1+3,x2+3,…,
xn+3的方差是( )
A.4 B.7
C.8 D.19
A
自主学习
6.
已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是 ,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数和方差分别是( )
A.2, B.2,1
C.4, D.4,3
D
自主学习
方差的应用
2
例 3
某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品 加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定 通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机 抽取15个,记录它们的质量(单位:g)如表所示.根据表中数据,你 认为快餐公司应该选购哪家加工厂的鸡腿?
典例分析
检查人员从甲、乙两家农副产品加工厂各随机抽取的15
个鸡腿分别组成一个样本,样本数据的平均数分别是
甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73
乙 75 73 79 72 76 71 73 72 78 74 77 78 80 71 75
解:
典例分析
样本数据的方差分别是
由 可知,两家加工厂的鸡腿质量大致相
等;由s甲2 < s乙2可知,甲加工厂的鸡腿质量更稳定,
大小更均匀. 因此,快餐公司应该选购甲加工厂生
产的鸡腿.
典例分析
归 纳
在比较两组数据时,一般先看平均数,在平均
数相同或相近的情况下,再分析稳定性问题,而方
差是反映数据的波动大小的量,通过比较方差的大
小来解决问题.
典例分析
1.
某跳远队准备从甲、乙两名运动员中选取成绩稳
定的一名参加比赛. 下表是这两名运动员10次测
验成绩(单位:m)
你认为应该选择哪名运动员参赛?为什么?
甲 5.85 5.93 6.07 5.91 5.99
6.13 5.98 6.05 6.00 6.19
乙 6.11 6.08 5.83 5.92 5.84
5.81 6.18 6.17 5.85 6.21
自主学习
x甲= ×(5.85+5.93+…+6.19)=6.01(m),
s甲2= ×[(5.85-6.01)2+(5.93-6.01)2+…
+(6.19-6.01)2]=0.009 54(m2),
x乙= ×(6.11+6.08+…+6.21)=6(m),
s乙2= ×[(6.11-6)2+(6.08-6)2+…+(6.21
-6)2]=0.024 34(m2).
因为s甲2解:
自主学习
2.
【中考·岳阳】现有甲、乙两个合唱队,队员的平
均身高为170 cm,方差分别是s甲2,s乙2,且s甲2>
s乙2,则两个队的队员的身高较整齐的是( )
A.甲队 B.乙队
C.两队一样整齐 D.不能确定
B
自主学习
3.
【中考·宁德】某创意工作室6位员工的月工资如图所示,因业务需要,现决定招聘一名新员工,若新员工的月工资为4 500元,则下列关于现在7位员工月工资的平均数和方差的说法正确的是( ) A.平均数不变,方差变大
B.平均数不变,方差变小
C.平均数不变,方差不变
D.平均数变小,方差不变
B
自主学习
4.
【中考·随州】为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书本数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A.5,5, B.5,5,10
C.6,5.5, D.5,5,
D
自主学习
5.
【中考·南充】某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:
成绩/分 36 37 38 39 40
人数/人 1 2 1 4 2
下列说法正确的是( )
A.这10名同学体育成绩的中位数为38分
B.这10名同学体育成绩的平均数为38分
C.这10名同学体育成绩的众数为39分
D.这10名同学体育成绩的方差为2
C
自主学习
6.
【中考·枣庄】下表记录了甲、乙、丙、丁四名
跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙
C.丙 D.丁
甲 乙 丙 丁
平均数/cm 185 180 185 180
方差 3.6 3.6 7.4 8.1
A
自主学习
方差
1.方差是用来衡量一组数据波动大小的重要统计量,反映
的是数据在平均数附近波动的情况,对于同类问题的两
组数据,方差越大,数据波动就越大,方差越小,数据
波动就越小;在统计中常用样本方差去估计总体方差.
2.一组数据的每一个数据都加上或减去同一个常数,所得
新数据的方差与原数据的方差相等.
3.一组数据的每一个数据都变为原数据的k倍,则所得新数
据的方差变为原数据方差的k2倍.
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版八下数学
精品同步教学课件
20.2 数据的波动程度
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
方差及其求法
1
问题 农科院计划为某地选择合适的甜玉米种子.选择
种子时,甜玉米的产量和产量的稳定性是农科院所关
心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10块自然条件相同的试验田进行试验,得
到各试验田每公顷的产量 (单位:t) 如下表所示.
问题引入
根据这些数据估计,农科院应该选择哪种甜玉米种子呢
上面两组数据的平均数分别是
甲 7.65 7.50 7.62 7.59 7.65 7.64 7.50 7.40 7.41 7.41
乙 7.55 7.56 7.53 7.44 7.49 7.52 7.58 7.46 7.53 7.49
说明在试验田中,甲、乙两种甜玉米的平均产量
相差不大.由此可以估计出这个地区种植这两种甜玉米,
它们的平均产量相差不大.
问题引入
为了直观地看出甲、乙两种甜玉米产量的情况,我们把
这两组数据画成下面的图20.2-1和图20.2-2.
问题引入
比较上面的两幅图可以看出,甲种甜玉米在各
试验田的产量波动较大, 乙 种甜玉米在各试验田的
产量较集中地分布在平均产量附近. 从图中看出的
结果能否用一个量来刻画呢?
问题引入
为了刻画一组数据波动的大小,可以采用很多
方法. 统计中常采用下面的 做法:设有n个数据x1,
x2 ,… ,xn,各数据与它们的平均数 的差的平方
分别是 … ,
我们用这些值的平均数,即用
来衡量这组数据波动的大小,并把它叫做这组数据
的方差,记作s2.
自主学习
例 1
人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:
=80,s2甲=240,s2乙=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
典例分析
在本题中,给出平均分和方差两种数据,那么平
均分要考查的是甲、乙两班的成绩的优劣,而成
绩的稳定性就要看两班成绩的方差了.那么所谓
的稳定性,也就是指成绩的波动.成绩波动越小,
成绩越稳定.根据“方差越大,数据的波动越大:
方差越小,数据的波动越小,我们很容易发现乙
班的方差比甲班的小,所以乙班的成绩较稳定.
分析:
典例分析
归 纳
在利用方差比较两组数据的波动情况时,一定要先
计算两组数据的平均数.一般说来,平均数可能反映数
据的优劣程度,如果在平均数上已经能够区分几组数据
的优劣,那么就不用再考虑方差的大小了.但在实际的
习题中,往往都是平均值相同,那么此时就要考虑数据
的方差情况了.由此可得到:在解决问题时,要先算平
均数,当平均值不同时,择优选取;当平均数相同时,
比较方差,选择波动较小的一组数据.
典例分析
例2
在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅 湖》, 参加表演的女演员的身高(单位:cm)如表所示.
哪个芭蕾舞团女演员的身高更整齐?
甲 163 164 164 165 165 166 166 167
乙 163 165 165 166 166 167 168 168
典例分析
甲、乙两团演员的身高平均数分别是
解:
方差分别是
由s甲2 < s乙2 可知,甲芭蕾舞团女演员的身高更整齐.
典例分析
归 纳
一般地,设n个数据x1,x2,…,xn的平均数为
,则方差
s2=
它反映了一组数据的波动大小,方差越大,波动性
越大,反之也成立.
典例分析
1.
【中考·自贡】对于一组统计数据3,3,6,5,
3. 下列说法错误的是( )
A.众数是3 B.平均数是4
C.方差是1.6 D.中位数是6
D
自主学习
2.
设数据x1,x2,…,xn的平均数为x,方差为s2,若s2=0,则( )
A.x=0
B.x1+x2+…+xn=0
C.x1=x2=…=xn=0
D.x1=x2=…=xn
D
自主学习
3.
【中考·通辽】若数据10,9,a,12,9的平均数是10,则这组数据的方差是( )
A.1 B.1.2
C.0.9 D.1.4
B
自主学习
4.
【中考·南京】若一组数据2,3,4,5,x的方
差与另一组数据5,6,7,8,9的方差相等,
则x的值为( )
A.1 B.6
C.1或6 D.5或6
C
自主学习
5.
【中考·遵义】如果一组数据x1,x2,…,xn的
方差是4,则另一组数据x1+3,x2+3,…,
xn+3的方差是( )
A.4 B.7
C.8 D.19
A
自主学习
6.
已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是 ,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数和方差分别是( )
A.2, B.2,1
C.4, D.4,3
D
自主学习
方差的应用
2
例 3
某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品 加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定 通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机 抽取15个,记录它们的质量(单位:g)如表所示.根据表中数据,你 认为快餐公司应该选购哪家加工厂的鸡腿?
典例分析
检查人员从甲、乙两家农副产品加工厂各随机抽取的15
个鸡腿分别组成一个样本,样本数据的平均数分别是
甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73
乙 75 73 79 72 76 71 73 72 78 74 77 78 80 71 75
解:
典例分析
样本数据的方差分别是
由 可知,两家加工厂的鸡腿质量大致相
等;由s甲2 < s乙2可知,甲加工厂的鸡腿质量更稳定,
大小更均匀. 因此,快餐公司应该选购甲加工厂生
产的鸡腿.
典例分析
归 纳
在比较两组数据时,一般先看平均数,在平均
数相同或相近的情况下,再分析稳定性问题,而方
差是反映数据的波动大小的量,通过比较方差的大
小来解决问题.
典例分析
1.
某跳远队准备从甲、乙两名运动员中选取成绩稳
定的一名参加比赛. 下表是这两名运动员10次测
验成绩(单位:m)
你认为应该选择哪名运动员参赛?为什么?
甲 5.85 5.93 6.07 5.91 5.99
6.13 5.98 6.05 6.00 6.19
乙 6.11 6.08 5.83 5.92 5.84
5.81 6.18 6.17 5.85 6.21
自主学习
x甲= ×(5.85+5.93+…+6.19)=6.01(m),
s甲2= ×[(5.85-6.01)2+(5.93-6.01)2+…
+(6.19-6.01)2]=0.009 54(m2),
x乙= ×(6.11+6.08+…+6.21)=6(m),
s乙2= ×[(6.11-6)2+(6.08-6)2+…+(6.21
-6)2]=0.024 34(m2).
因为s甲2
自主学习
2.
【中考·岳阳】现有甲、乙两个合唱队,队员的平
均身高为170 cm,方差分别是s甲2,s乙2,且s甲2>
s乙2,则两个队的队员的身高较整齐的是( )
A.甲队 B.乙队
C.两队一样整齐 D.不能确定
B
自主学习
3.
【中考·宁德】某创意工作室6位员工的月工资如图所示,因业务需要,现决定招聘一名新员工,若新员工的月工资为4 500元,则下列关于现在7位员工月工资的平均数和方差的说法正确的是( ) A.平均数不变,方差变大
B.平均数不变,方差变小
C.平均数不变,方差不变
D.平均数变小,方差不变
B
自主学习
4.
【中考·随州】为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书本数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A.5,5, B.5,5,10
C.6,5.5, D.5,5,
D
自主学习
5.
【中考·南充】某校数学兴趣小组在一次数学课外活动中,随机抽查该校10名同学参加今年初中学业水平考试的体育成绩,得到结果如下表所示:
成绩/分 36 37 38 39 40
人数/人 1 2 1 4 2
下列说法正确的是( )
A.这10名同学体育成绩的中位数为38分
B.这10名同学体育成绩的平均数为38分
C.这10名同学体育成绩的众数为39分
D.这10名同学体育成绩的方差为2
C
自主学习
6.
【中考·枣庄】下表记录了甲、乙、丙、丁四名
跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙
C.丙 D.丁
甲 乙 丙 丁
平均数/cm 185 180 185 180
方差 3.6 3.6 7.4 8.1
A
自主学习
方差
1.方差是用来衡量一组数据波动大小的重要统计量,反映
的是数据在平均数附近波动的情况,对于同类问题的两
组数据,方差越大,数据波动就越大,方差越小,数据
波动就越小;在统计中常用样本方差去估计总体方差.
2.一组数据的每一个数据都加上或减去同一个常数,所得
新数据的方差与原数据的方差相等.
3.一组数据的每一个数据都变为原数据的k倍,则所得新数
据的方差变为原数据方差的k2倍.
课堂小结
https://www.21cnjy.com/help/help_extract.php
