人教版数学八年级下册 第18章本章复习与测试 课件(共23张PPT)
文档属性
| 名称 | 人教版数学八年级下册 第18章本章复习与测试 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 16:05:06 | ||
图片预览







文档简介
(共23张PPT)
章末复习
1.系统回顾本章主要知识,能运用相关知识解决具体问题.
2.系统地梳理知识间的联系,进一步加深对本章知识的理解和运用.
复习导入
《平行四边形》这章中,特殊四边形的性质与判定较多,但联系紧密,区别难分、易混,为了进一步弄清它们的联系与区别.这节课我们一起将本章知识结构、知识要点进行复习梳理.
自主复习
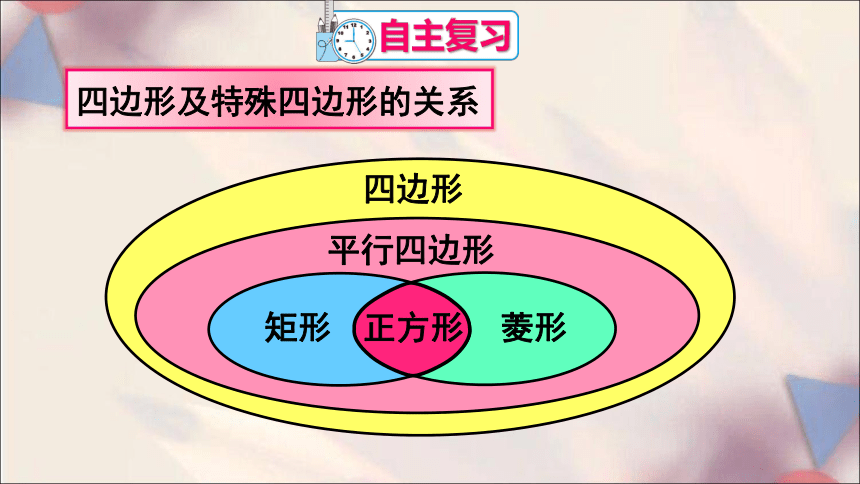
矩形
菱形
正方形
平行四边形
四边形
四边形及特殊四边形的关系
平行四
边形
矩形
菱形
正方形
四边形
a
b
c
d
e
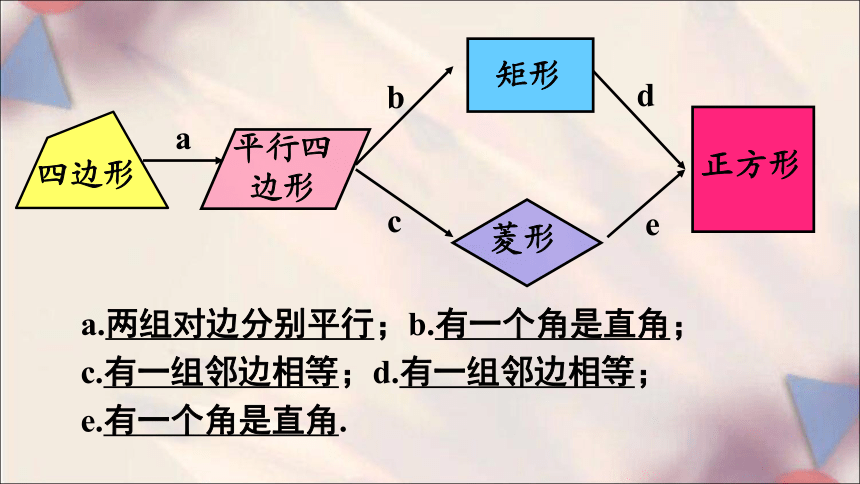
a.两组对边分别平行;b.有一个角是直角;
c.有一组邻边相等;d.有一组邻边相等;
e.有一个角是直角.
平行四边形
平行四边形的两组对边分别相等.
平行四边形的两组对角分别相等.
平行四边形的对角线互相平分.
性质
对角线互相平分的四边形是平行四边形.
判定
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
矩形
直角三角形斜边上的中线等于斜边的一半.
矩形的四个角都是直角.
矩形的两条对角线相等.
性质
判定
对角线相等的平行四边形式矩形.
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
菱形
菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.
菱形的四条边都相等.
菱形的对角都相等.
性质
判定
四条边都相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
正方形
性质
正方形是轴对称图形,它有四条对称轴.
正方形的四个角都是直角;
正方形的四条边都相等;
正方形的对角线相等,并且互相垂直平分;
判定
有一组邻边相等的矩形是正方形.
有一个角为直角的菱形是正方形.
各种平行四边形的研究中,它们各自的研究内容、研究步骤、研究方法有什么共同点?
研究内容 研究步骤 研究方法
平行四边形
矩形
菱形
正方形
边、角、对
角线的特征
边、角、对
角线的特征
边、角、对
角线的特征
边、角、对
角线的特征
下定义→探性 质→研判定
下定义→探性 质→研判定
下定义→探性 质→研判定
下定义→探性 质→研判定
观察、猜想、证明;把四边形问
题转化为三角形问题;从性质定
理的逆命题讨论中研究判定定理
一般到特殊的方法,
类比平行四边形
一般到特殊的方法,类
比平行四边形和矩形
一般到特殊的方法,
类比矩形和菱形
典例解析
【例1】如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:①BE=DF;②∠AEB=∠DFC;③AF∥EC.请你从中选择一个适当的条件____,使四边形AECF是平行四边形,并证明你的结论.
证明:如图,连接AC交BD于O.
∴AO=CO,OB=OD.
又∵BE=DF,∴OB-BE=OD-DF,∴OE=OF.
又∵AO=CO,
∴四边形AECF为平行四边形.
①
【例2】如图,点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,试判断四边形EFGH的形状,并证明你的结论.
解:四边形EFGH为平行四边形.
如图,连接AC,在△ACD中,H、G分别为AD、CD的中点,
∴HG∥AC,HG= AC,
同理:EF∥AC,EF= AC,
∴HG∥EF,HG=EF.
∴四边形EFGH为平行四边形.
【例3】如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求高DH的长.
解:∵四边形ABCD为菱形,
∴AO= AC=4cm,AC⊥BD,
∴在Rt△AOB中,
(cm).
S△ABD= DH · AB= AO · BD
∴DH= (cm).
【例4】如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点,如果两个正方形的边长相等,那么正方形A′B′C′O绕点O无论怎样转动,两个正方形重叠部分的面积总等于一个正方形面积的四分之一,你能说明理由吗?
解:∵∠BOF+∠A′OB=90°,∠A′OB+∠AOE=90°.
∴∠BOF=∠AOE. 又∵OA=OB,∠OAE=∠OBF.
∴△AOE≌△BOF.∴S△AOE=S△BOF .
∴S四边形EBFO=S△BOF+S△OEB
=S△AOE+S △OEB
= S正方形ABCD.
【例5】如图,△ABC中,BD,CE为高,F是边BC的中点,判断△DEF的形状,并说明理由.
解:△DEF为等腰三角形.
在Rt△BEC中,∵F为BC的中点,
∴EF= BC.
同理:FD= BC.
∴FD=EF,
∴ △DEF为等腰三角形.
随堂演练
基础巩固
1.下列图形:矩形、菱形、等腰梯形、正方形中对称轴最多的是( )
A.矩形 B.菱形 C.等腰梯形 D.正方形
D
2.如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长是( )
A.1 B.2
C.1.5 D.3
B
3.如图所示,直线l过正方形ABCD的顶点B. A,C两点到直线l的距离分别为5和12,
则正方形的边长是____.
13
4.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,
则PE+PF=____.
综合应用
5.已知:如图,BC是等腰三角形BED底边ED的高,四边形ABEC是平行四边形.求证:四边形ABCD是矩形.
证明:∵BC是等腰三角形BED底边ED的高,∴BC⊥ED,EC=CD.
又∵四边形ABEC是平行四边形,
∴AB∥EC,即AB∥CD,AB=EC=CD.
∴四边形ABCD是平行四边形.
又∵BC⊥ED,∴四边形ABCD是矩形.
拓展延伸
6.如图,四边形ABCD、DEFG都是正方形,连接AE、CG.(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.(提示:找全等三角形)
(1)证明:∵∠ADC=∠GDE=90°,
∴∠ADC+∠ADG=∠GDE+∠ADG,
即∠GDC=∠ADE. 又∵CD=AD,
DG=DE,∴△GCD≌△EAD,∴AE=CG.
(2)解:AE⊥CG.∵由(1)知△GCD≌△EAD,∴∠GCD=∠EAD. 又∵∠ANM=∠CND,
∴∠AMN=∠CDN=90°,∴AE⊥CG.
章末复习
1.系统回顾本章主要知识,能运用相关知识解决具体问题.
2.系统地梳理知识间的联系,进一步加深对本章知识的理解和运用.
复习导入
《平行四边形》这章中,特殊四边形的性质与判定较多,但联系紧密,区别难分、易混,为了进一步弄清它们的联系与区别.这节课我们一起将本章知识结构、知识要点进行复习梳理.
自主复习
矩形
菱形
正方形
平行四边形
四边形
四边形及特殊四边形的关系
平行四
边形
矩形
菱形
正方形
四边形
a
b
c
d
e
a.两组对边分别平行;b.有一个角是直角;
c.有一组邻边相等;d.有一组邻边相等;
e.有一个角是直角.
平行四边形
平行四边形的两组对边分别相等.
平行四边形的两组对角分别相等.
平行四边形的对角线互相平分.
性质
对角线互相平分的四边形是平行四边形.
判定
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
矩形
直角三角形斜边上的中线等于斜边的一半.
矩形的四个角都是直角.
矩形的两条对角线相等.
性质
判定
对角线相等的平行四边形式矩形.
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
菱形
菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.
菱形的四条边都相等.
菱形的对角都相等.
性质
判定
四条边都相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
正方形
性质
正方形是轴对称图形,它有四条对称轴.
正方形的四个角都是直角;
正方形的四条边都相等;
正方形的对角线相等,并且互相垂直平分;
判定
有一组邻边相等的矩形是正方形.
有一个角为直角的菱形是正方形.
各种平行四边形的研究中,它们各自的研究内容、研究步骤、研究方法有什么共同点?
研究内容 研究步骤 研究方法
平行四边形
矩形
菱形
正方形
边、角、对
角线的特征
边、角、对
角线的特征
边、角、对
角线的特征
边、角、对
角线的特征
下定义→探性 质→研判定
下定义→探性 质→研判定
下定义→探性 质→研判定
下定义→探性 质→研判定
观察、猜想、证明;把四边形问
题转化为三角形问题;从性质定
理的逆命题讨论中研究判定定理
一般到特殊的方法,
类比平行四边形
一般到特殊的方法,类
比平行四边形和矩形
一般到特殊的方法,
类比矩形和菱形
典例解析
【例1】如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:①BE=DF;②∠AEB=∠DFC;③AF∥EC.请你从中选择一个适当的条件____,使四边形AECF是平行四边形,并证明你的结论.
证明:如图,连接AC交BD于O.
∴AO=CO,OB=OD.
又∵BE=DF,∴OB-BE=OD-DF,∴OE=OF.
又∵AO=CO,
∴四边形AECF为平行四边形.
①
【例2】如图,点E、F、G、H分别为四边形ABCD的边AB、BC、CD、DA的中点,试判断四边形EFGH的形状,并证明你的结论.
解:四边形EFGH为平行四边形.
如图,连接AC,在△ACD中,H、G分别为AD、CD的中点,
∴HG∥AC,HG= AC,
同理:EF∥AC,EF= AC,
∴HG∥EF,HG=EF.
∴四边形EFGH为平行四边形.
【例3】如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求高DH的长.
解:∵四边形ABCD为菱形,
∴AO= AC=4cm,AC⊥BD,
∴在Rt△AOB中,
(cm).
S△ABD= DH · AB= AO · BD
∴DH= (cm).
【例4】如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点,如果两个正方形的边长相等,那么正方形A′B′C′O绕点O无论怎样转动,两个正方形重叠部分的面积总等于一个正方形面积的四分之一,你能说明理由吗?
解:∵∠BOF+∠A′OB=90°,∠A′OB+∠AOE=90°.
∴∠BOF=∠AOE. 又∵OA=OB,∠OAE=∠OBF.
∴△AOE≌△BOF.∴S△AOE=S△BOF .
∴S四边形EBFO=S△BOF+S△OEB
=S△AOE+S △OEB
= S正方形ABCD.
【例5】如图,△ABC中,BD,CE为高,F是边BC的中点,判断△DEF的形状,并说明理由.
解:△DEF为等腰三角形.
在Rt△BEC中,∵F为BC的中点,
∴EF= BC.
同理:FD= BC.
∴FD=EF,
∴ △DEF为等腰三角形.
随堂演练
基础巩固
1.下列图形:矩形、菱形、等腰梯形、正方形中对称轴最多的是( )
A.矩形 B.菱形 C.等腰梯形 D.正方形
D
2.如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长是( )
A.1 B.2
C.1.5 D.3
B
3.如图所示,直线l过正方形ABCD的顶点B. A,C两点到直线l的距离分别为5和12,
则正方形的边长是____.
13
4.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上,PE⊥AC于E,PF⊥BD于F,
则PE+PF=____.
综合应用
5.已知:如图,BC是等腰三角形BED底边ED的高,四边形ABEC是平行四边形.求证:四边形ABCD是矩形.
证明:∵BC是等腰三角形BED底边ED的高,∴BC⊥ED,EC=CD.
又∵四边形ABEC是平行四边形,
∴AB∥EC,即AB∥CD,AB=EC=CD.
∴四边形ABCD是平行四边形.
又∵BC⊥ED,∴四边形ABCD是矩形.
拓展延伸
6.如图,四边形ABCD、DEFG都是正方形,连接AE、CG.(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.(提示:找全等三角形)
(1)证明:∵∠ADC=∠GDE=90°,
∴∠ADC+∠ADG=∠GDE+∠ADG,
即∠GDC=∠ADE. 又∵CD=AD,
DG=DE,∴△GCD≌△EAD,∴AE=CG.
(2)解:AE⊥CG.∵由(1)知△GCD≌△EAD,∴∠GCD=∠EAD. 又∵∠ANM=∠CND,
∴∠AMN=∠CDN=90°,∴AE⊥CG.
