有理数的加法
图片预览





文档简介
课件16张PPT。有理数的加法执教人:冉瑞金义务教育课程标准实验教科书人教版七年级数学上册二0一一年九月二十一日引 言
一.回顾旧知识
1、有理数的绝对值是怎样定义的?如何计算一个数的绝对值?
(1)、绝对值的定义:一个数的绝对值是表示该数的点与原点的距离。
(2)、求绝对值的方法:
①、一个正数的绝对值是它本身
②、零的绝对值是零
③、一个负数的绝对值是它的相反数
2、比较下列各组数的大小,并说说各组中哪一个数的绝对值大?
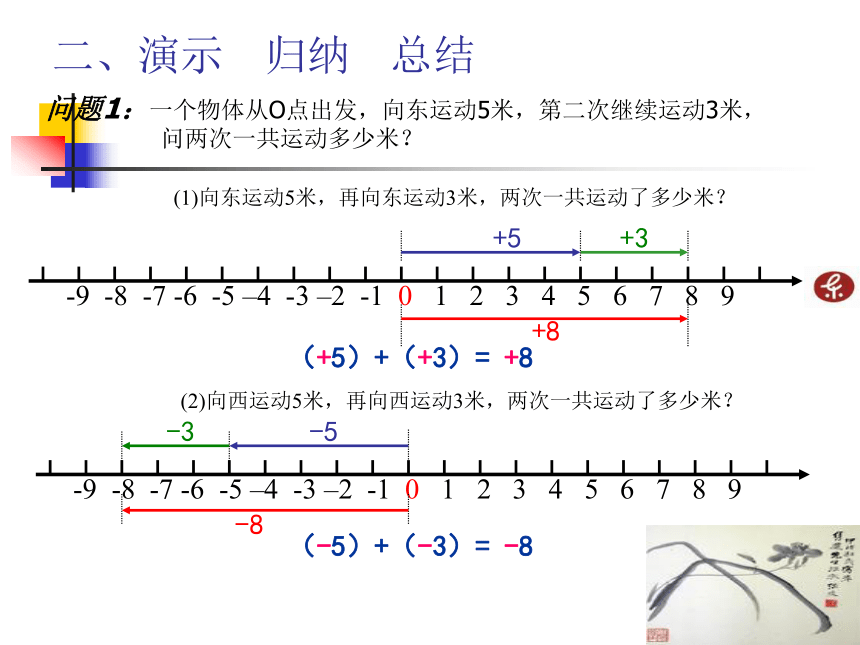
(1)7和4; (2)-7和4; (3)7和-4; (4)-7和-4。同学们,在小学里,我们已经学习了加、减、乘、除四则运算,当时学习的运算是在正有理数和零的范围内,然而在实际问题中,我们运算的数有可能超出正数范围。如:“北京某天的气温是5℃~-3℃,它当天的温差是多少?”该如何计算。要解决这些问题,下面我们就来探索。有理数的加法二、演示 归纳 总结问题1:一个物体从O点出发,向东运动5米,第二次继续运动3米,问两次一共运动多少米?
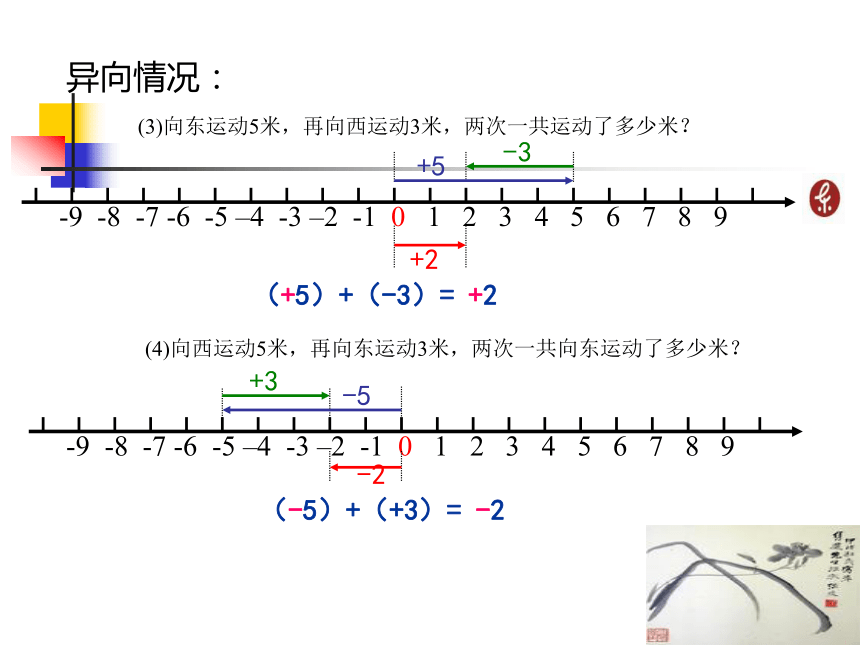
(1)向东运动5米,再向东运动3米,两次一共运动了多少米?+5+3+8(+5)+(+3)= +8 (2)向西运动5米,再向西运动3米,两次一共运动了多少米? -3-5-8(-5)+(-3)= -8 由上面的两个例子我们可以得出下面的结论: 同号两数相加,取相同的符号,并且把它们的绝对值相加. 异向情况:(3)向东运动5米,再向西运动3米,两次一共运动了多少米? +2(+5)+(-3)= +2 +5-3(4)向西运动5米,再向东运动3米,两次一共向东运动了多少米? +3-5-2(-5)+(+3)= -2 由上面的两个例子我们可以得出下面的结论: 异号两数相加, 绝对值不相等时,取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值问题2:一个物体从O点出发,向东运动5米,再向东运动 -5米,两次一共向东运动了多少米? (+5)+(-5)= 0 +5-5由上面的例子我们可以得出下面的结论: 互为相反数的两个数相加得0问题3:一个物体从O点出发,向东运动-5米,再向东运动0米,两次一共向东运动了多少米? 结论:一个数同零相加,仍得这个数. -5(-5)+ 0 = -5 由上面的例子我们可以得出下面的结论: 一个数与0相加,
仍得这个数.
有理数加法法则
1.同号两数相加,取相同的符号,并且把它们的绝对值相加.
2.异号两数相加, 绝对值不相等时,取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值
3.互为相反数的两个数相加得0.
4. 一个数与0相加,仍得这个数.
从有理数的加法法则可以得出:
如果两个数的和等于0,
那么两个数互为相反数.四、课堂小结1、本堂课我们学习了有理数的加法运算法则:
2、有理数的加法运算中,首先应该先判断类型(同号、异号、相反数),然后确定和的符号,最后计算和的绝对值。
3、有理数的加法打破了算术数加法中和一定大于加数的常规。三、巩固练习一、计算:
(1)、(-7)+(-5)= 运用了法则:
(2)、(-10)+0= 运用了法则:
(3)、(+2)+(-8)= 运用了法则:
(4)、(+3.5)+(-3.5)= 运用了法则
二、教材24页:习题1.3第一题加油吧!!!再见
一.回顾旧知识
1、有理数的绝对值是怎样定义的?如何计算一个数的绝对值?
(1)、绝对值的定义:一个数的绝对值是表示该数的点与原点的距离。
(2)、求绝对值的方法:
①、一个正数的绝对值是它本身
②、零的绝对值是零
③、一个负数的绝对值是它的相反数
2、比较下列各组数的大小,并说说各组中哪一个数的绝对值大?
(1)7和4; (2)-7和4; (3)7和-4; (4)-7和-4。同学们,在小学里,我们已经学习了加、减、乘、除四则运算,当时学习的运算是在正有理数和零的范围内,然而在实际问题中,我们运算的数有可能超出正数范围。如:“北京某天的气温是5℃~-3℃,它当天的温差是多少?”该如何计算。要解决这些问题,下面我们就来探索。有理数的加法二、演示 归纳 总结问题1:一个物体从O点出发,向东运动5米,第二次继续运动3米,问两次一共运动多少米?
(1)向东运动5米,再向东运动3米,两次一共运动了多少米?+5+3+8(+5)+(+3)= +8 (2)向西运动5米,再向西运动3米,两次一共运动了多少米? -3-5-8(-5)+(-3)= -8 由上面的两个例子我们可以得出下面的结论: 同号两数相加,取相同的符号,并且把它们的绝对值相加. 异向情况:(3)向东运动5米,再向西运动3米,两次一共运动了多少米? +2(+5)+(-3)= +2 +5-3(4)向西运动5米,再向东运动3米,两次一共向东运动了多少米? +3-5-2(-5)+(+3)= -2 由上面的两个例子我们可以得出下面的结论: 异号两数相加, 绝对值不相等时,取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值问题2:一个物体从O点出发,向东运动5米,再向东运动 -5米,两次一共向东运动了多少米? (+5)+(-5)= 0 +5-5由上面的例子我们可以得出下面的结论: 互为相反数的两个数相加得0问题3:一个物体从O点出发,向东运动-5米,再向东运动0米,两次一共向东运动了多少米? 结论:一个数同零相加,仍得这个数. -5(-5)+ 0 = -5 由上面的例子我们可以得出下面的结论: 一个数与0相加,
仍得这个数.
有理数加法法则
1.同号两数相加,取相同的符号,并且把它们的绝对值相加.
2.异号两数相加, 绝对值不相等时,取绝对值较大的加数的符号,并且用较大的绝对值减去较小的绝对值
3.互为相反数的两个数相加得0.
4. 一个数与0相加,仍得这个数.
从有理数的加法法则可以得出:
如果两个数的和等于0,
那么两个数互为相反数.四、课堂小结1、本堂课我们学习了有理数的加法运算法则:
2、有理数的加法运算中,首先应该先判断类型(同号、异号、相反数),然后确定和的符号,最后计算和的绝对值。
3、有理数的加法打破了算术数加法中和一定大于加数的常规。三、巩固练习一、计算:
(1)、(-7)+(-5)= 运用了法则:
(2)、(-10)+0= 运用了法则:
(3)、(+2)+(-8)= 运用了法则:
(4)、(+3.5)+(-3.5)= 运用了法则
二、教材24页:习题1.3第一题加油吧!!!再见
