第四章 几何图形认识初步导学案
文档属性
| 名称 | 第四章 几何图形认识初步导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 132.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-28 00:00:00 | ||
图片预览



文档简介
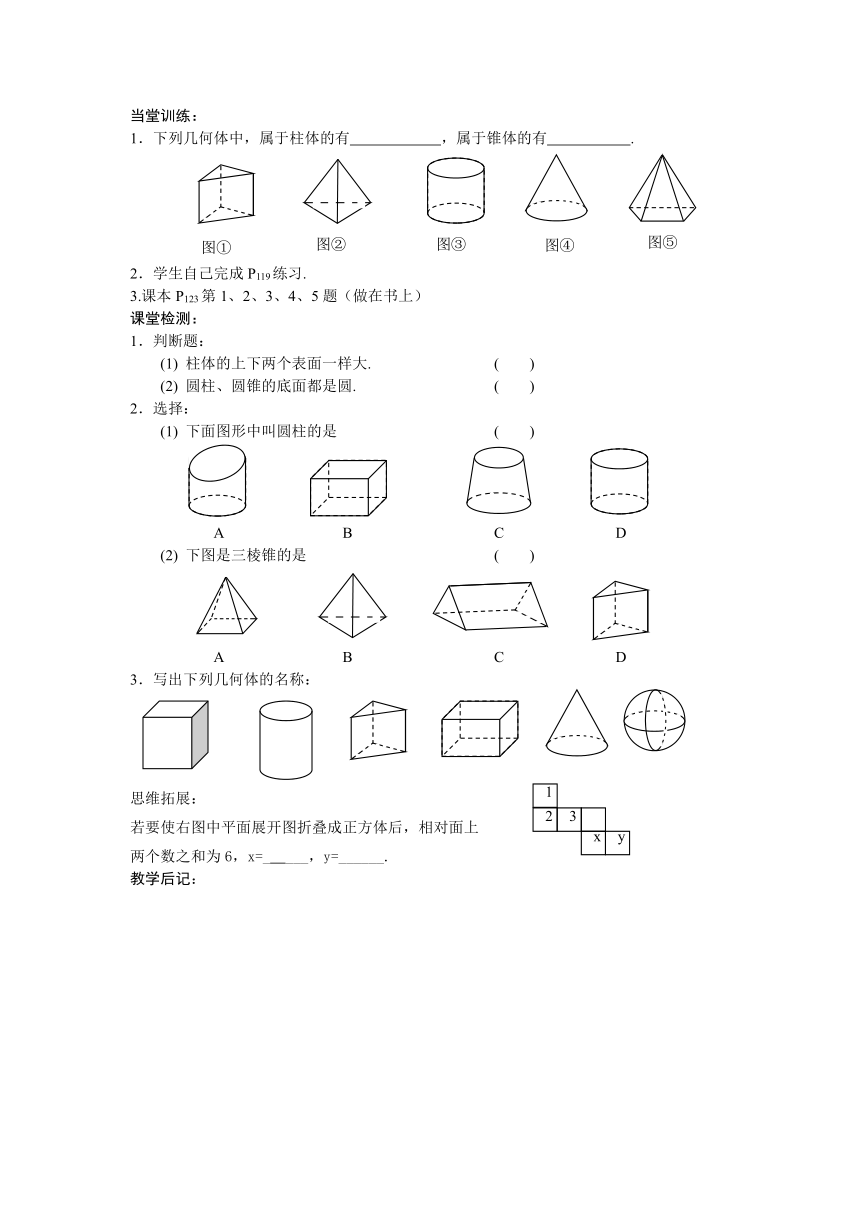
4.1 多姿多彩的图形(1)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.初步认识立体图形和平面图形的概念;
2.能从具体物体中抽象出长方体、正方体、圆柱、球、圆锥、棱柱、棱锥等立体图形.
教学重点:认识立体图形,发展几何直觉.
教学难点:从实物中抽象立体图形.
教学过程:
预习导学:
1.几何图形分立体图形和平面图形:都在同一平面的图形是 图形;不在同一平面的图形是 图形.
2.长方体、正方体、球、圆柱等都是 图形.
3.矩形、正方形、圆都是 图形.
4.写出下图中各图的名称:
5.学生自学完成课本P118,思考题.
合作探究.
比较下面这些图形,看看这些图形有什么相同的地方,有什么不同的地方?
小结:
1.图①②所表示的立体图形我们把它叫做 体;
图③⑤所表示的立体图形我们把它叫做 体;
图④所表示的立体图形我们把它叫做 体.
2.圆柱的侧面是由 组成,棱柱的侧面是由 组成,圆锥的侧面是由 组成,棱锥的侧面是由 组成.
思考:常见的立体图形可分为哪几种类型,柱体的特征是什么?锥体的特征是什么?柱体和锥体有什么不同?
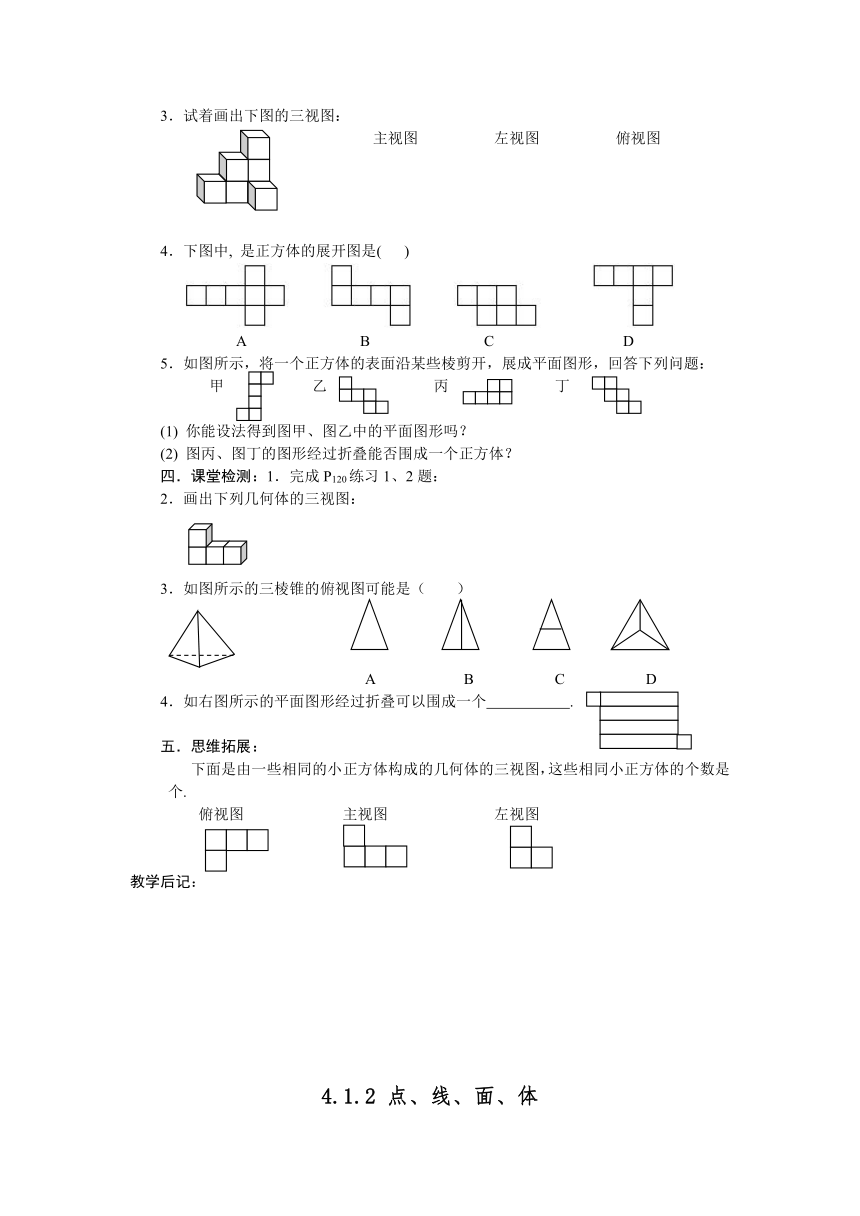
当堂训练:
1.下列几何体中,属于柱体的有 ,属于锥体的有 .
2.学生自己完成P119练习.
3.课本P123第1、2、3、4、5题(做在书上)
课堂检测:
1.判断题:
(1) 柱体的上下两个表面一样大. ( )
(2) 圆柱、圆锥的底面都是圆. ( )
2.选择:
(1) 下面图形中叫圆柱的是 ( )
A B C D
(2) 下图是三棱锥的是 ( )
A B C D
3.写出下列几何体的名称:
思维拓展:
若要使右图中平面展开图折叠成正方体后,相对面上
两个数之和为6,x=_ ___,y=______.
教学后记:
4.1 丰富多彩的图形(2)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:经历从不同方面观察几何物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果.
教学重点:体验从不同方向看同一物体可能看到不同的结果.
教学难点:从不同方向看同一物体的不同结果表述.
教学过程:
一.预习导学:
学生自学P119—120,然后每人制作一个教学模具:①正方体 ②长方体 ③圆锥 ④圆柱
二.合作探究:
1.展示学生制作的教具:正方体、长方体、圆锥、圆柱. 请同学们从正面、左面、上面看图形,把看到的平面图分别画出来:
(1) 圆柱: 从正面看 从左面看 从上面看
(2) 圆锥: 从正面看 从左面看 从上面看
(3) 正方体: 从正面看 从左面看 从上面看
归纳:我们把从几何体的正面看到的的平面图形叫做主视图,从上面看到的叫做俯视图,从左面看到的叫做左视图. 把主视图、俯视图、左视图称为几何体的三视图.
2.将正方体、长方体、圆柱、圆锥模具沿表面适当的剪开得到平面图形,此平面图形称为相应的立体图形的展开图. 教者具体操作让学生认真观察正方体、长方体、圆柱、圆锥的展开图.
三.当堂训练:
1.观察P119图4.1-7,试着画出它的主视图、左视图和俯视图.
2.观察P119图4.1—8,完成下列问题:
(1) 此图是由 个正方体组成的 图形.
(2) 用自己制作的小正方体摆放出此立体图形.
(3) 观察摆放出的立体图形,分别从正面、左面、上面不同角度观察.
(4) 画出这个立体图形的三视图.
2.P120图4.1-10分别是哪个立体图形的展开图.
3.试着画出下图的三视图:
主视图 左视图 俯视图
4.下图中, 是正方体的展开图是( )
A B C D
5.如图所示,将一个正方体的表面沿某些棱剪开,展成平面图形,回答下列问题:
甲 乙 丙 丁
(1) 你能设法得到图甲、图乙中的平面图形吗?
(2) 图丙、图丁的图形经过折叠能否围成一个正方体?
四.课堂检测:1.完成P120练习1、2题:
2.画出下列几何体的三视图:
3.如图所示的三棱锥的俯视图可能是( )
A B C D
4.如右图所示的平面图形经过折叠可以围成一个 .
五.思维拓展:
下面是由一些相同的小正方体构成的几何体的三视图,这些相同小正方体的个数是 个.
俯视图 主视图 左视图
教学后记:
4.1.2 点、线、面、体
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
识记点、线、面、体的概念;理解点、线、面、体之间的关系.
教学重点:点、线、面、体之间的关系.
教学难点:理解点动成线、线动成面、面动成体.
教学过程:
一.预习导学:
活动一:观察长方体盒子. 想一想:长方体是由哪几部分组成的?它有几个面?面与面相交形成几条线?线与线相交形成几个点?
活动二:观察实物:圆柱、圆锥回答下列问题.
1.上述物体的底面和侧面有何不同?
2.面与面相交所得的线与活动一中所得的线有何不同?
活动三:讨论下列问题:
1.流星是怎样形成的?为什么会出现一条亮线?
2.线运动形成了什么?举例说明.
3.面运动形成了什么?举例说明.
二.新课学习:
1.我们学过的几何体有 、 、 、 、 、________、________等.
2.包围着体的是 ,面有 面和 两种.
3.面与面相交的地方形成 ,线有 线和 线两种.
4.线和线相交的地方是 .
5.点、线、面、体之间的关系是:点动成 ,线动成 ,面动成 .
6.几何图形都是由 、 、 、 组成的, 是构成图形的基本元素. ____、___、 、 经过运动变化,就能组成各种各样的几何图形,形成多姿多彩的图形世界.
三.课堂检测:
1.下列各图形绕虚线旋转一周,能够形成什么样的几何体.
2.如右图,正方体截去一个角后,剩下的几何体的面数和棱数分别为( )
A.6,13 B.7,15
C.6,15 D.7,14
3.P122练习.
4.填空:
(1) 请同学们手拿一个硬币,将其立在桌面上用力一转,它形成的是一个 体.
(2) 正方体有 个顶点,经过每个顶点有 条棱,它共有 条棱.
(3) 圆柱的底面是 ,侧面是 ,展开后的侧面是 .
(4) 圆锥的侧面是 ,底面是 ,展开后的侧面是 .
(5) 棱柱的侧面是 ,分为 棱柱和 棱柱.
四.课堂检测:
1.圆可以分割成几个扇形 ( )
A.2个 B.4个 C.8个 D.无数个
2.下列立体图形是由右边哪个三角形绕直线l旋转得到的 ( )
A B C D
3.下列立体图形是如何旋转而成的?( )
A B C D
4、画出将Rt⊿ABC(∠C=90°),绕斜边AB旋转一周所得几何体的主视图.
主视图是:
思维拓展:
将如图所示的正方体沿某些棱展开后,能得到的图形是( )
A. B. C. D.
教学后记:
4.2 直线、射线、线段(1)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.初步掌握直线、射线、线段的基本知识;
2.增强几何语言的概括、表达能力.
教学重点:两点确定一条直线.
教学难点:直线、射线、线段的区别.
教学过程:
一.预习导学:
1.指导学生阅读课本P128探究,完成下列问题.
(1) 过一点的直线有 条,过两点的直线有 条.
(2) 直线是 的,并且向 无限延伸着的.
(3) 过两点有 条直线,并且 一条直线,简称 .
2.直线的表示方法:
(1) 点的表示方法:点常用 来表示,一个大写字母表示一个点,不同的点要用不同的 来表示.
(2) 直线的表示方法:①一条直线可以用 来表示;②一条直线也可以用__________来表示.
如图(1)记作 ;图(2)记作_________;图(3)记作_________或_________.
3.直线的性质:①直线_________端点,可以向_________延伸;
②直线公理:________________________.
4.如图:A、B、C、D四个点中任意三个点不在同一直线上,试画出所有的直线.
5.点和直线的位置有_________和_________两种. 如图:点P在直线l_____;点Q在直线l_____.
二.新课学习:
1.画一画:
(1) 画直线AB.
(2) 画射线CD.
(3) 画线段EF.
2.归纳:________________________叫做射线,如图 ,射线是______的一部分,有___个端点,向____无限延伸.
3.射线的表示方法:
① 用两个大写字母表示:一条射线可以用它的端点和射线上另一点来表示,端点字母必须_____________;如图 ,表示为__________或__________.
② 用一个小写字母表示. 如图 ,表示为___________.
4.线段的概念:直线上___________________叫做线段,这两个点叫做_______.
5.线段的表示:如图:①用两个端点的大写字母表示.记作_________或_________;②用一个小写字母表示.记作________.
6.直线、射线、线段三个概念的区别如下表:
图形
表示法
长度
作图叙述
端点
直线
直线AB或BA
无限
过点A、B作直线AB
无
射线
射线AB
无限
过点A、B作射线AB
一个
线段
线段AB或BA
有限
连接AB
两个
7.如图: 中有______条线段.
三.课堂检测:
1.把一根木条固定在墙上,至少要钉____个钉子,因为________________.
2.如图,直线a上有四个点,则图中有____条直线,____条射线,____条线段.
3.如图,点C在直线______上,点A在直线BC____,B点是直线_____与直线_____的交点.
4.画一画,如图A、B、C三点不在同一直线上.
(1) 过A、B两点作直线.
(2) 作射线BC.
(3) 连接AC.
四.思维拓展:
往返于甲、乙两地的客车,中途停靠三个站.
(1) 问有多少种不同的票价.
(2) 准备多少种车票.
教学后记:
4.2 直线、射线、线段(2)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.会用两种方法比较两条线段的大小;
2.会用尺规画一条线段等于已知线段,作两条线段的和与差;
3.理解线段的中点,两点之间的距离的概念及线段的性质.
教学重点:1.画一条线段等于已知线段; 2.线段的中点概念.
教学难点:用几何方法比较两条线段的大小,用线段的中点概念求线段的长.
教学过程:
一.预习导学:
1.比较两同学的身高有几种方法?
2.要比较两条线段的大小,你能想出哪些方法?
3.自学课本P130,完成以下问题.
已知:线段a,b.
(1) 作线段AB=a.
(2) 作线段CD=a+b.
(3) 作线段EF=a-b.
4.如图:C点是线段AB的中点,则有AC=_______=_______.
如图:C、D是线段PQ的三等分点,则有PC=_______=_______=_______.
5.两点的所有连线中,______最短,简称___________________.
6.连接两点间的____________叫做这两点间的距离.
二.应用迁移,巩固提高:
例1.已知线段a,b.
求作线段AB=2a-b.
作法:
1.作射线AM.
2.在射线AM上顺次截取AC=CD=a.
3.在线段AD上截取DB=b.
则线段AB=__________.
例2.已知线段AB=6cm,在直线AB上画线段BC,使BC=2cm. 求线段AC的长.
分析:如图(1),当C点在线段AB的延长线上时,AC=_____+_____=______;如图(2) 当C在线段AB上时,AC=_____-_____=______.
请同学们自己完成解答过程:
例3.已知:如图,点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点. 求MN的长.
分析:M为AC中点,CM=____=_____;N为BC中点,CM=____=_____;则MN=__________.
学生完成解答过程:
例4.延长线段AB到C,使BC=AB,D为AC的中点且DC=6cm,求AB的长.
分析:(1) 按要求画出图形;(2)由于D是AC的中点,则有AC=___DC=____cm;(3) 由于BC=AB,所以BC=___AC=____cm;(4) 而AB=AC-BC=___-___=___cm.
学生自己完成解答过程:
三.课堂检测:
1.按图形填空:如图
(1) AC=AB+____+____;AC=____+____;CD=AD-____;
(2) 已知AB=CD=5cm,AC=13cm,则BD=____cm.
2.已知:线段AB=4cm,在直线AB上截取BC=6cm,则AC=____cm.
3.下列语句中正确的是 ( )
A.延长直线AB B.延长线段AB至C,使AC=BC
C.延长射线OA D.延长线段AB至C,使BC=2AB
4.若射线AD上有三个点B、C、D,则共有射线 ( )
A.1条 B.3条 C.4条 D.5条
5.在一条直线上顺次取A、B、C三点,使AB=5cm,BC=2cm,取AC中点O,赇线段OB的长.
四.思维拓展:
如图所示,线段AB=4.8,C是它的一个三等分点,D是它的中点. 求CD的长?DC是AB的几分之几?BD是AC的几分之几?
教学后记:
4.3.1 角(1)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.理解角的形成,知道角的有关概念,角的两种定义和四种表示方法;
2.会进行度、分、秒间单位互化及角的和、差、倍、分计算.
教学重点:
1.对角定义的理解,角的表示方法,角的度量.
2.平角、周角的概念以及它们与直线、射线的区别.
教学过程:
一.自学课本P136内容,完成下面问题.
角的两种定义:
1.角的概念:(1) 根据生活中的实例,如钟面上的时针与分针,自己试着画一个角.
(2) 观察讨论: 叫角, 是角的顶点, 是角的两条边.
(3) 每人在(1) 所画的角上标明顶点,两条边.
2.角的旋转定义:(1) 拿出预先准备的一段毛线,把它看成射线OA,使射线OA绕着点O旋转,使终止位置OB和起始位置OA成一直线时,就形成平角.它的顶点是 ,两条分别是 、 . 继续旋转,OB与OA重合时,就形成 .即角可以看作由 旋转而形成的图形。
(2) 归纳总结:从(1)可以看出,角可以看作是 的图形.
角的表示方法:
(1) 用三个大写的 表示. 注意:中间位置上的字母表示角的 . 前后两个字母分别是除顶点外的角的 上的点.
画角: 记为: 或 .
(2) 用一个大写的 表示. 注意:这个字母必须是表示 的字母. 若用一个大写的 表示角时,顶点处只能有一个角,否则不能用这种方法表示.
画角: 记为: 或 或 .
(3) 用一个 数字表示. 表示方法:通常在表示角的位置上面画出弧线,并在弧线处标注数字.
画图: 记为:
(4) 用一个小写的 字母表示,表示方法:通常在表示角的位置上面画出弧线,并在弧线处标注数字.
画图: 记为:
二.自学课本P137,回答下列问题:
1.一副三角板含有哪些度数的角?
2.(1) 是常用的角的度量单位;
(2) 1周角= °,1平角= °,1直角= °,1周角= 平角= 直角.
(3) 把一周角360等分,每一份就是 度的角,记作 ;把1度的角60等分,每一份叫做 分的角,记作 ;把1分的角60等分,每一等份叫做 秒的角,记作 .
(4) 以度、分、秒为单位的角的度量制叫 度制.还有 制、 制等。
当堂训练:
课本P138练习第1、2、3题.
课堂检测:
1.用一副三角尺分别画出30°、60°、90°、135°的角.
2.3.32小时= 小时 分 秒 3.32°= ° ′ ″;
12小时9分36秒= 小时 12°9′36″= °
3.(1) 把26.29°转化为度、分、秒表示的形式.
(2) 把33°24′36″转化成度表示的形式.
4.判断下列说法是否正确.
(1) 两条射线组成的图形叫做角. ( )
(2) 平角的两条边成一条直线. ( )
(3) 直线是平角. ( )
(4) 周角是一条射线. ( )
(5) 射线是周角. ( )
4.画射线OA、OB,在∠AOB的内部和外部
分别画射线OC、OD. 说出此图形中一共有多
少个角,请分别写出.
思维拓展:
1.计算:(1) 13°29′+78°37″ (2) 23°53′×3+107°43′÷5
2.如图,分别表示出以点B、D为顶点的角.
教学后记:
4.3.1 角(2)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1、能借助三角板画特殊角,借助量角器画任何给定度数的角。
2、理解尺规作图的意义,熟练掌物尺规作一个角等于已知角的方法。
教学重点:
会用三角板和量角器画角及尺规作图。
教学难点:
用直尺和圆规画一个角等于已知角。
教学过程:
预习导学:
在工程修建测量中,用到经纬仪,经纬仪是测量角的大小的仪器,还有其他度量角的工具吗?
用三角板画特殊角。
用一副三角板画出30°、45°、60°、90°的角。
能利用一副三角板画出15°、75°、105°、135°、165°的角吗?试一试。
分析:15°= + 75°= + 105°= +
135°= + 165°= + +
画出图形:
(3)用一副三角板可以画出 的角。
二、合作探究:
1、用量角器画出给定的角:
思考用量角器画角的步骤是什么?
用量角器画112°、76°的角。
用尺规画角。
教师演示:用无刻度的直尺和圆规画一个角等于已知角即∠AOB.
学生讨论:角的顶点和角的一边如何确定?角的另一边怎样画出?画图的关键是什么?
量一量,∠A'O'B'与∠AOB相等吗?
归纳作法:1、任画一条射线O'A';
2、以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
3、以O'为圆心,OC长为半径画弧交O'A'于 C';
4、以C'为圆心,CD长为半径画弧与前弧交于D';
5、过D'作射线O'B';
∠A'O'B'就是所要求作的角。
说明:(1)在数学中,把只用直尺(无刻度的)和圆规画图称为尺规作图。
(2)在画图过程中画出的图形(点、线、弧线等),也叫作图痕迹,这些痕迹必须保留。
(3)图画好后,要写出画图结论。
三、课堂检测:
已知∠ABC,求作∠A'B'C',使∠A'B'C'=2∠ABC.
四、思维拓展:
如图,已知两个锐角、,其中2∠>∠,画一个角,使它等于2∠-∠
教学后记
4.3.2 角的比较与运算
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.会比较两个角的大小,能估计一个角的大小,在操作中认识角的平分线;
2.知道两个角的大小比较方法;
3.会进行有关角的计算.
教学重点:角的计算.
教学难点:角的识图.
教学过程:
一.预习导学:
1.怎样比较两条线段的长短?(口述)
2.类似地,如何比较两个角的大小呢?
与线段长短比较类似,我们可以用 量出角的度数,然后比较它们的大小;也可以把它们 在一起比较大小.
二.合作探究:
(一) 1.叠合法:从“形”的方面进行比较.
把两个角的顶点和一边分别重合,另外两条边落在重合边的同旁,通过另一边的位置关系比较大小.
学习课本P138,观察图4.3—6,讨论回答课本P 138思考问题.
2.度量法:从“数”的方面比较,分别量出每个角的度数.
归纳:
(1) 两个角的大小关系有 种;
(2) 角的 关系与角的 关系一致;
(3) 角的大小只与 有关,而与 无关,因为角的边是 而不是 .
3.角平分线:
如图1,如果∠AOB=∠BOC,那么∠AOC=2 =2 ,∠AOB= = . 像OB这样,从一个角的 出发,把这个角分成 的 .叫做这个角的平分线.
归纳:(1) 角的平分线是从角的顶点出发的一条 ;
(2) 这条射线把这个角分成 的角.
(二) 例题学习:
1.学习课本P140例1,回答下列问题:
分析:(1) AB是直线,所以AOB是 角,它是 度.
(2) ∠AOB=∠ +∠ ;∠BOC=∠ -∠ .
(3) 写出解答过程.
2.学习课本P140例2.
(三) 课堂训练:课本P140练习题1、2、3题.
(四) 课堂检测:
1.如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.
(1) 2∠BOC是哪个角? (2) ∠BOD是哪个角?
(3) ∠AOB+∠BOC等于哪个角?
(4) 求∠AOB和∠BOD的度数.
2.如图,将一副三角板叠放在一起,使直角顶点重合于O,求∠AOC+∠DOB的度数.
思维拓展:
如图,将一张长方形的纸斜折过去,使角顶点A落在A′处,BC为折痕,然后把BE边折过去,使之与A′B边重合,折痕为BD,那么两折痕BC、BD间的夹角是多少度?
教学后记:
4.3.3 余角和补角(一)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.掌握互为余角,互为补角的概念;
2.会正确表示一个角的余角或补角;
3.能熟练地求出一个角的余角或补角.
教学重点:互余、互补角的概念.
教学难点:互余和互补角的正确判断.
教学过程:
一.预习导学:
1.观察一副三角尺,你能说出每一个角的度数吗?在每一个三角尺中,两个锐角的和是多少度?
2.如图1、2,过平角∠AOB、直角∠COD作射线OM、ON,射线OM、ON把平角∠AOB、直角∠COD分别分成几个角?它们的度数关系如何?
二.合作探究:
1.学习课本P141内容,填空:
(1) 两个角的度数的和是90°,那么这两个角叫做 ,简称 ,即其中一个角是另一个角的 .
(2) 两个角的度数的和是180°,那么这两个角叫做 ,简称 ,即其中一个角是另一个角的 .
(3) 角α的余角可以表示为 ,补角可以表示为 .
温馨提示:(1) 互为余角,互为补角是指两个角而非一个角;
(2) 互为余角,互为补角与两个角所处的位置无关.
2.例题学习
学习课本P142例3,填空:
由∠1与∠2互补,可得∠2=180°- ;
由∠3与∠4互补,可得∠4=180°- ,因为∠1=∠3;所以 = .
归纳:等角的补角相等,等角的余角相等.
三.当堂训练:
1.课本P144第8题.
2.(1) 如果∠1+∠2=90°,∠2+∠3=90°,那么∠1与∠3的关系是 .
(2) 一个锐角的补角比这个角的余角大 .
(3) 若一个角的余角是这个角的,则这个角是 ,这个角的补角是 .
3.一个角的补角加上10°后等于这个角的余角的3倍,求这个角的度数.
四.课堂检测:
1.若两个角的和与两角的差之和等于1个平角的度数,则这两个角( )
A.一个是锐角,一个是钝角 B.都是钝角
C.必有一个是直角 D.两个都是直角
2.(1) 一个角的余角与补角也互为补角,这个角是 .
(2) 互为余角且相等的角是 ,互为补角且相等的角是 .
3.如图,AOE是一条直线,∠AOB=∠COD=90°,如果∠1=30°,那么∠2= ,∠3= . 和∠1互为余角的角有 ,和∠1相等的角有 .
五.思维拓展:
如图,∠AOB=90°,OM平分∠AOC、ON平分∠BOC. 求∠MON的度数.
教学后记:
4.3.3 余角和补角(二)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:正确理解方位角,能画出方位角所表示方向的射线;
教学重点:画出方位角所表示方向的射线.
教学难点:能用方位角知识解决实际问题.
教学过程:
一.预习导学:
1.(1) 若∠1+∠2=90°,∠1+∠3=90°,则∠1与∠2是 关系,∠1与∠3是 关系,∠2与∠3是 关系,根据 .
(2) 若∠1+∠2=180°,∠3+∠4=180°,则∠1与∠2是 关系,∠3与∠4是 关系,∠2与∠3是 关系,根据 .
2.如图,在△ABC中,AC⊥BC,CD⊥AB于D,若已知∠1+∠3=90°,∠2+∠4=90°,且∠1+∠2=90°. 请指出图中所有相等的角.
二.合作探究:
1.在日常生活中,八个方向是不够用的,如果要准确表示方向,就要引导方位角的概念.
例如:OA表示北偏东30°方向的一条射线,仿照上述方向,你能表示下列方向吗?
(1) 南偏东60° ( )
(2) 北偏西60° ( )
(3) 东南方向 ( )
(4) 南北方向 ( )
(5) 东西方向 ( )
(6) 西南方向 ( )
注意:方位角的表示方法:先写南或北,再写偏东或偏西多少度.
2.例题学习:
学习课本P142例4,填空:
画法:找客轮B,以点 为顶点,表示 方向的射线为角的一边,画 的角,使它的另一边 落在东与北之间,射线OB的方向就是 ,即客轮B所在方向.请你在图中画出表示货轮C和海岛D方向的射线.
三.当堂训练:
1.课本P144第9题.
2.如图所示,射线OA表示的方向是 ,射线OB表示的方向是 ,射线OC表示的方向是 .
3.甲从O点出发,沿北偏西30°方向走了50米,到达A点,乙也从O点出发,沿南偏东35°方向走了80米到达B点. 求∠AOB.
四.课堂检测:
1.如图,指出OA是表示什么方向的一条射线?仿照这条射线画出表示下列方向的射线:
(1) 南偏东60°;(2) 北偏西70°;(3) 西南方向.
2.“海神”号货轮从A港出发,先沿东北方向(北偏东45°)行驶50km,再沿北偏西30°方向行驶35km,到达目的地. 问目的地在A港什么方向?
五.思维拓展:
如图,小华有一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,现在知道C地在A地的北偏东30°,在B地南偏东45°,你能帮小华确定C地的位置吗?
教学后记:
第四章 小结
课型:复习课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.复习几何图形中有关概念;
2.本章基础知识运用.
教学过程:
一.完成知识图解(学生自学)
二.知识点应用:
1.填空:(1) 圆柱的底面是 ,侧面是 ,展开后的侧面是 .
(2) 棱柱的侧面是 ,分为 棱柱和 棱柱;圆可以分割成 个扇形.
(3) 如图是一个正方体展开图,将它折叠成正方体后,“建”字对面是 .
(4) 两根木条,一根长60cm,一根长100cm,将它们的一端重合,顺次放在同一条直线上,此时两根木条的中点间的距离是 cm.
(5) 已知∠α=37°25′,∠β=52°48′,则∠α+∠β= .
(6) 1.36°= ° ′ ″
(7) 已知∠α的余角是50°,则∠α的补角的度数是 .
2.计算:(1) 把角度9.03°化为度、分、秒,再求它们的余角和补角.
(2) 如图,点O在直线AC上,OD平分∠AOB,∠EOC=2∠BOE,∠DOE=72°,求∠EOC.
三.课堂检测:
1.(1)23°45′+24°15′ (2) 23°53′×3+107°43′÷5
2.一个角的余角比它的补角的少20°,求这个角.
3.如图,∠AOB=79°,∠DOC=25°,OD平分∠AOC.
求∠BOC的度数.
四.探索题:如图,OA的方向是北偏东15°,OB的方向是北偏西30°.
(1) 若∠AOC=∠AOB,则OC的方向是 .
(2) OD是OB的反向延长线,OD的方向是 .
(3) ∠BOD可看做是OB绕O逆时针方向旋转至OD,作∠BOD的平分线OE,并用方位角表示OE的方向.
(4) 在(1) (2) (3)的条件下,求∠COE.
教学后记:
第四章 单元检测
(满分:100分) 姓名______________
一、选择题(每小题3分,共18分)
1.下列说法正确的是( )
A.直线AB和直线BA是两条直线; B.射线AB和射线BA是两条射线;
C.线段AB和线段BA是两条线段; D.直线AB和直线a不能是同一条直线。
2.下列图中角的表示方法正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.下面图形经过折叠可以围成一个棱柱的是( )
A. B.
D.
4.将如图所示的正方体沿某些棱展开后,能得到的图形是( )
A. B. C. D.
5.若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
6.经过任意三点中的两点共可画出( )
A.1条直线 B.2条直线 C.1条或3条直线 D.3条直线
二、填空题(每小题3分,共12分)
7.有公共顶点的两条射线分别表示南偏15°与北偏东25°,则这两条射线组成的角的度数为_____________________.
8.如图,若CB = 4 cm,DB = 7 cm,且D是AC的中点,则AC =_________________.
9.八时三十分,时针与分针夹角度数是_______.
10.如图,从学校A到书店B最近的路线是①号路线,其道理用几何知识解释应是_____________________________________.
三、解答题(每小题10分,共30分) 11.计算:
12.一个角的余角比它的补角的还少40°,求这个角。
13.如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数。
(填空10 )
四、试一试,探一探(每小题20分)
14.如图,BO、CO分别平分∠ABC和∠ACB,
(1)若∠A = 60°,求∠O; (2)若∠A =100°、120°,∠O又是多少?
(3)由(1)、(2)你又发现了什么规律?当∠A的度数发生变化后,你的结论仍成立吗? (提示:三角形的内角和等于180°)
15.如图,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点。
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC + CB = a cm,其它条件不变,你能猜想MN的长度吗?并说明理由。你能用一句简洁的话描述你发现的结论吗?
(3)若C在线段AB的延长线上,且满足ACBC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由。
第四章单元测验试题
姓名 班别 成绩
一、填空题(第2题1分一空,其余2分一空,共32分)
1、已知线段AB=8cm,延长AB至C,使AC=2AB,D是AB中点,则线段CD=____ __.
2、57.32°=_______°_______′_______″;27°14′24″=___ __°.
4、已知∠a=36°42′15″,那么∠a的余角等于________.
5、∠1+∠2=180°,∠2+∠3=180°,根据___ __ ___,得∠1=∠3.
6、102°43′32″+77°16′28″=_____ ___;98°12′25″÷5=___ __.
7、如图是某些几何体的表面展开图,则这些几何体分别是
图1:
图2:
图3:
8、若要使图中平面展开图按虚线折叠成正方体后,相对面上
两个数之和为6,x=_ ___,y=______.
9、要在墙上固定一根木条,至少要 个钉子,
根据的原理是 。
10、不在同一直线上的四点最多能确定????????? 条直线。
11、小明每天下午5:30回家,这时分针与时针所成的角的度数为___________。
二、选择题(3分一题、共36分)
1.如图1所示的棱柱有( )
A.4个面 B.6个面 C.12条棱 D.15条棱
2.如图2,从正面看可看到△的是( )
3.下列语句正确的是( )
A.如果PA=PB,那么P是线段AB的中点; B.作∠AOB的平分线CD
C.连接A、B两点得直线AB; D.反向延长射线OP(O为端点)
4. 对于直线,线段,射线,在下列各图中能相交的是(?????? )
5.如果与互补,与互余,则与的关系是(?????? )
(A)= (B) (C) (D)以上都不对
6.下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个的是(??? )
?
?
?
7.如图,,,点B、O、D在同一直线上,则的度数(????? )
(A) (B) (C) (D)
8.下列图中角的表示方法正确的个数有( )
(A)1个 (B)2个 (C)3个 (D)4个
9.如图的几何体,左视图是 ( )
10.下列叙述正确的是(???? )
?A.180°的角是补角????????B.110°和90°的角互为补角
C.10°、20°、60°的角互为余角? D.120°和60°的角互为补角
11.如图,点A位于点O的 方向上.( ).
(A)南偏东35° (B)北偏西65° (C)南偏东65° (D)南偏西65°
12. 将下列图形绕直线l旋转一周, 可以得到右图所示的立体图形的是( )
三、作图题
1.根据下列要求画图:(6分)
(1)连接线段AB;(2)画射线OA,射线OB;
(3)在线段AB上取一点C,在射线OA上取一
点D(点C、D不与点A重合),画直线CD,使
直线CD与射线OB交于点E。
2. 用尺规画出下列图形:已知、、()
求作线段AB使AB=。(不要求写画法)?(6分)
?
?
四、解答题
1.如图,D是AB的中点, E是BC的中点,BE=AC=2cm,线段DE的长,
求线段DE的长. (5分)
2.如图,点A、O、E在同一直线上,∠AOB=40°,∠EOD=28°46’,OD平分∠COE,
求∠COB的度数(5分)
B C
D
A O E
3.一个角的补角与它的余角的度数的3倍,求这个角的度数.(5分)
解:设这个角为,则它的补角为 ,余角为 ,依题意得
4.如图,∠AOD=∠BOC=90°,∠COD=42°,求∠AOC、∠AOB的度数. (5分)
3.如下图,在已知角内画射线,画1条射线,图中共有 个角;画2条射线,图中共有 个角;画3条射线,图中共有 个角,
求画n条射线所得的角的个数。(9分)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.初步认识立体图形和平面图形的概念;
2.能从具体物体中抽象出长方体、正方体、圆柱、球、圆锥、棱柱、棱锥等立体图形.
教学重点:认识立体图形,发展几何直觉.
教学难点:从实物中抽象立体图形.
教学过程:
预习导学:
1.几何图形分立体图形和平面图形:都在同一平面的图形是 图形;不在同一平面的图形是 图形.
2.长方体、正方体、球、圆柱等都是 图形.
3.矩形、正方形、圆都是 图形.
4.写出下图中各图的名称:
5.学生自学完成课本P118,思考题.
合作探究.
比较下面这些图形,看看这些图形有什么相同的地方,有什么不同的地方?
小结:
1.图①②所表示的立体图形我们把它叫做 体;
图③⑤所表示的立体图形我们把它叫做 体;
图④所表示的立体图形我们把它叫做 体.
2.圆柱的侧面是由 组成,棱柱的侧面是由 组成,圆锥的侧面是由 组成,棱锥的侧面是由 组成.
思考:常见的立体图形可分为哪几种类型,柱体的特征是什么?锥体的特征是什么?柱体和锥体有什么不同?
当堂训练:
1.下列几何体中,属于柱体的有 ,属于锥体的有 .
2.学生自己完成P119练习.
3.课本P123第1、2、3、4、5题(做在书上)
课堂检测:
1.判断题:
(1) 柱体的上下两个表面一样大. ( )
(2) 圆柱、圆锥的底面都是圆. ( )
2.选择:
(1) 下面图形中叫圆柱的是 ( )
A B C D
(2) 下图是三棱锥的是 ( )
A B C D
3.写出下列几何体的名称:
思维拓展:
若要使右图中平面展开图折叠成正方体后,相对面上
两个数之和为6,x=_ ___,y=______.
教学后记:
4.1 丰富多彩的图形(2)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:经历从不同方面观察几何物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果.
教学重点:体验从不同方向看同一物体可能看到不同的结果.
教学难点:从不同方向看同一物体的不同结果表述.
教学过程:
一.预习导学:
学生自学P119—120,然后每人制作一个教学模具:①正方体 ②长方体 ③圆锥 ④圆柱
二.合作探究:
1.展示学生制作的教具:正方体、长方体、圆锥、圆柱. 请同学们从正面、左面、上面看图形,把看到的平面图分别画出来:
(1) 圆柱: 从正面看 从左面看 从上面看
(2) 圆锥: 从正面看 从左面看 从上面看
(3) 正方体: 从正面看 从左面看 从上面看
归纳:我们把从几何体的正面看到的的平面图形叫做主视图,从上面看到的叫做俯视图,从左面看到的叫做左视图. 把主视图、俯视图、左视图称为几何体的三视图.
2.将正方体、长方体、圆柱、圆锥模具沿表面适当的剪开得到平面图形,此平面图形称为相应的立体图形的展开图. 教者具体操作让学生认真观察正方体、长方体、圆柱、圆锥的展开图.
三.当堂训练:
1.观察P119图4.1-7,试着画出它的主视图、左视图和俯视图.
2.观察P119图4.1—8,完成下列问题:
(1) 此图是由 个正方体组成的 图形.
(2) 用自己制作的小正方体摆放出此立体图形.
(3) 观察摆放出的立体图形,分别从正面、左面、上面不同角度观察.
(4) 画出这个立体图形的三视图.
2.P120图4.1-10分别是哪个立体图形的展开图.
3.试着画出下图的三视图:
主视图 左视图 俯视图
4.下图中, 是正方体的展开图是( )
A B C D
5.如图所示,将一个正方体的表面沿某些棱剪开,展成平面图形,回答下列问题:
甲 乙 丙 丁
(1) 你能设法得到图甲、图乙中的平面图形吗?
(2) 图丙、图丁的图形经过折叠能否围成一个正方体?
四.课堂检测:1.完成P120练习1、2题:
2.画出下列几何体的三视图:
3.如图所示的三棱锥的俯视图可能是( )
A B C D
4.如右图所示的平面图形经过折叠可以围成一个 .
五.思维拓展:
下面是由一些相同的小正方体构成的几何体的三视图,这些相同小正方体的个数是 个.
俯视图 主视图 左视图
教学后记:
4.1.2 点、线、面、体
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
识记点、线、面、体的概念;理解点、线、面、体之间的关系.
教学重点:点、线、面、体之间的关系.
教学难点:理解点动成线、线动成面、面动成体.
教学过程:
一.预习导学:
活动一:观察长方体盒子. 想一想:长方体是由哪几部分组成的?它有几个面?面与面相交形成几条线?线与线相交形成几个点?
活动二:观察实物:圆柱、圆锥回答下列问题.
1.上述物体的底面和侧面有何不同?
2.面与面相交所得的线与活动一中所得的线有何不同?
活动三:讨论下列问题:
1.流星是怎样形成的?为什么会出现一条亮线?
2.线运动形成了什么?举例说明.
3.面运动形成了什么?举例说明.
二.新课学习:
1.我们学过的几何体有 、 、 、 、 、________、________等.
2.包围着体的是 ,面有 面和 两种.
3.面与面相交的地方形成 ,线有 线和 线两种.
4.线和线相交的地方是 .
5.点、线、面、体之间的关系是:点动成 ,线动成 ,面动成 .
6.几何图形都是由 、 、 、 组成的, 是构成图形的基本元素. ____、___、 、 经过运动变化,就能组成各种各样的几何图形,形成多姿多彩的图形世界.
三.课堂检测:
1.下列各图形绕虚线旋转一周,能够形成什么样的几何体.
2.如右图,正方体截去一个角后,剩下的几何体的面数和棱数分别为( )
A.6,13 B.7,15
C.6,15 D.7,14
3.P122练习.
4.填空:
(1) 请同学们手拿一个硬币,将其立在桌面上用力一转,它形成的是一个 体.
(2) 正方体有 个顶点,经过每个顶点有 条棱,它共有 条棱.
(3) 圆柱的底面是 ,侧面是 ,展开后的侧面是 .
(4) 圆锥的侧面是 ,底面是 ,展开后的侧面是 .
(5) 棱柱的侧面是 ,分为 棱柱和 棱柱.
四.课堂检测:
1.圆可以分割成几个扇形 ( )
A.2个 B.4个 C.8个 D.无数个
2.下列立体图形是由右边哪个三角形绕直线l旋转得到的 ( )
A B C D
3.下列立体图形是如何旋转而成的?( )
A B C D
4、画出将Rt⊿ABC(∠C=90°),绕斜边AB旋转一周所得几何体的主视图.
主视图是:
思维拓展:
将如图所示的正方体沿某些棱展开后,能得到的图形是( )
A. B. C. D.
教学后记:
4.2 直线、射线、线段(1)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.初步掌握直线、射线、线段的基本知识;
2.增强几何语言的概括、表达能力.
教学重点:两点确定一条直线.
教学难点:直线、射线、线段的区别.
教学过程:
一.预习导学:
1.指导学生阅读课本P128探究,完成下列问题.
(1) 过一点的直线有 条,过两点的直线有 条.
(2) 直线是 的,并且向 无限延伸着的.
(3) 过两点有 条直线,并且 一条直线,简称 .
2.直线的表示方法:
(1) 点的表示方法:点常用 来表示,一个大写字母表示一个点,不同的点要用不同的 来表示.
(2) 直线的表示方法:①一条直线可以用 来表示;②一条直线也可以用__________来表示.
如图(1)记作 ;图(2)记作_________;图(3)记作_________或_________.
3.直线的性质:①直线_________端点,可以向_________延伸;
②直线公理:________________________.
4.如图:A、B、C、D四个点中任意三个点不在同一直线上,试画出所有的直线.
5.点和直线的位置有_________和_________两种. 如图:点P在直线l_____;点Q在直线l_____.
二.新课学习:
1.画一画:
(1) 画直线AB.
(2) 画射线CD.
(3) 画线段EF.
2.归纳:________________________叫做射线,如图 ,射线是______的一部分,有___个端点,向____无限延伸.
3.射线的表示方法:
① 用两个大写字母表示:一条射线可以用它的端点和射线上另一点来表示,端点字母必须_____________;如图 ,表示为__________或__________.
② 用一个小写字母表示. 如图 ,表示为___________.
4.线段的概念:直线上___________________叫做线段,这两个点叫做_______.
5.线段的表示:如图:①用两个端点的大写字母表示.记作_________或_________;②用一个小写字母表示.记作________.
6.直线、射线、线段三个概念的区别如下表:
图形
表示法
长度
作图叙述
端点
直线
直线AB或BA
无限
过点A、B作直线AB
无
射线
射线AB
无限
过点A、B作射线AB
一个
线段
线段AB或BA
有限
连接AB
两个
7.如图: 中有______条线段.
三.课堂检测:
1.把一根木条固定在墙上,至少要钉____个钉子,因为________________.
2.如图,直线a上有四个点,则图中有____条直线,____条射线,____条线段.
3.如图,点C在直线______上,点A在直线BC____,B点是直线_____与直线_____的交点.
4.画一画,如图A、B、C三点不在同一直线上.
(1) 过A、B两点作直线.
(2) 作射线BC.
(3) 连接AC.
四.思维拓展:
往返于甲、乙两地的客车,中途停靠三个站.
(1) 问有多少种不同的票价.
(2) 准备多少种车票.
教学后记:
4.2 直线、射线、线段(2)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.会用两种方法比较两条线段的大小;
2.会用尺规画一条线段等于已知线段,作两条线段的和与差;
3.理解线段的中点,两点之间的距离的概念及线段的性质.
教学重点:1.画一条线段等于已知线段; 2.线段的中点概念.
教学难点:用几何方法比较两条线段的大小,用线段的中点概念求线段的长.
教学过程:
一.预习导学:
1.比较两同学的身高有几种方法?
2.要比较两条线段的大小,你能想出哪些方法?
3.自学课本P130,完成以下问题.
已知:线段a,b.
(1) 作线段AB=a.
(2) 作线段CD=a+b.
(3) 作线段EF=a-b.
4.如图:C点是线段AB的中点,则有AC=_______=_______.
如图:C、D是线段PQ的三等分点,则有PC=_______=_______=_______.
5.两点的所有连线中,______最短,简称___________________.
6.连接两点间的____________叫做这两点间的距离.
二.应用迁移,巩固提高:
例1.已知线段a,b.
求作线段AB=2a-b.
作法:
1.作射线AM.
2.在射线AM上顺次截取AC=CD=a.
3.在线段AD上截取DB=b.
则线段AB=__________.
例2.已知线段AB=6cm,在直线AB上画线段BC,使BC=2cm. 求线段AC的长.
分析:如图(1),当C点在线段AB的延长线上时,AC=_____+_____=______;如图(2) 当C在线段AB上时,AC=_____-_____=______.
请同学们自己完成解答过程:
例3.已知:如图,点C在线段AB上,且AC=6cm,BC=4cm,点M、N分别是AC、BC的中点. 求MN的长.
分析:M为AC中点,CM=____=_____;N为BC中点,CM=____=_____;则MN=__________.
学生完成解答过程:
例4.延长线段AB到C,使BC=AB,D为AC的中点且DC=6cm,求AB的长.
分析:(1) 按要求画出图形;(2)由于D是AC的中点,则有AC=___DC=____cm;(3) 由于BC=AB,所以BC=___AC=____cm;(4) 而AB=AC-BC=___-___=___cm.
学生自己完成解答过程:
三.课堂检测:
1.按图形填空:如图
(1) AC=AB+____+____;AC=____+____;CD=AD-____;
(2) 已知AB=CD=5cm,AC=13cm,则BD=____cm.
2.已知:线段AB=4cm,在直线AB上截取BC=6cm,则AC=____cm.
3.下列语句中正确的是 ( )
A.延长直线AB B.延长线段AB至C,使AC=BC
C.延长射线OA D.延长线段AB至C,使BC=2AB
4.若射线AD上有三个点B、C、D,则共有射线 ( )
A.1条 B.3条 C.4条 D.5条
5.在一条直线上顺次取A、B、C三点,使AB=5cm,BC=2cm,取AC中点O,赇线段OB的长.
四.思维拓展:
如图所示,线段AB=4.8,C是它的一个三等分点,D是它的中点. 求CD的长?DC是AB的几分之几?BD是AC的几分之几?
教学后记:
4.3.1 角(1)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.理解角的形成,知道角的有关概念,角的两种定义和四种表示方法;
2.会进行度、分、秒间单位互化及角的和、差、倍、分计算.
教学重点:
1.对角定义的理解,角的表示方法,角的度量.
2.平角、周角的概念以及它们与直线、射线的区别.
教学过程:
一.自学课本P136内容,完成下面问题.
角的两种定义:
1.角的概念:(1) 根据生活中的实例,如钟面上的时针与分针,自己试着画一个角.
(2) 观察讨论: 叫角, 是角的顶点, 是角的两条边.
(3) 每人在(1) 所画的角上标明顶点,两条边.
2.角的旋转定义:(1) 拿出预先准备的一段毛线,把它看成射线OA,使射线OA绕着点O旋转,使终止位置OB和起始位置OA成一直线时,就形成平角.它的顶点是 ,两条分别是 、 . 继续旋转,OB与OA重合时,就形成 .即角可以看作由 旋转而形成的图形。
(2) 归纳总结:从(1)可以看出,角可以看作是 的图形.
角的表示方法:
(1) 用三个大写的 表示. 注意:中间位置上的字母表示角的 . 前后两个字母分别是除顶点外的角的 上的点.
画角: 记为: 或 .
(2) 用一个大写的 表示. 注意:这个字母必须是表示 的字母. 若用一个大写的 表示角时,顶点处只能有一个角,否则不能用这种方法表示.
画角: 记为: 或 或 .
(3) 用一个 数字表示. 表示方法:通常在表示角的位置上面画出弧线,并在弧线处标注数字.
画图: 记为:
(4) 用一个小写的 字母表示,表示方法:通常在表示角的位置上面画出弧线,并在弧线处标注数字.
画图: 记为:
二.自学课本P137,回答下列问题:
1.一副三角板含有哪些度数的角?
2.(1) 是常用的角的度量单位;
(2) 1周角= °,1平角= °,1直角= °,1周角= 平角= 直角.
(3) 把一周角360等分,每一份就是 度的角,记作 ;把1度的角60等分,每一份叫做 分的角,记作 ;把1分的角60等分,每一等份叫做 秒的角,记作 .
(4) 以度、分、秒为单位的角的度量制叫 度制.还有 制、 制等。
当堂训练:
课本P138练习第1、2、3题.
课堂检测:
1.用一副三角尺分别画出30°、60°、90°、135°的角.
2.3.32小时= 小时 分 秒 3.32°= ° ′ ″;
12小时9分36秒= 小时 12°9′36″= °
3.(1) 把26.29°转化为度、分、秒表示的形式.
(2) 把33°24′36″转化成度表示的形式.
4.判断下列说法是否正确.
(1) 两条射线组成的图形叫做角. ( )
(2) 平角的两条边成一条直线. ( )
(3) 直线是平角. ( )
(4) 周角是一条射线. ( )
(5) 射线是周角. ( )
4.画射线OA、OB,在∠AOB的内部和外部
分别画射线OC、OD. 说出此图形中一共有多
少个角,请分别写出.
思维拓展:
1.计算:(1) 13°29′+78°37″ (2) 23°53′×3+107°43′÷5
2.如图,分别表示出以点B、D为顶点的角.
教学后记:
4.3.1 角(2)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1、能借助三角板画特殊角,借助量角器画任何给定度数的角。
2、理解尺规作图的意义,熟练掌物尺规作一个角等于已知角的方法。
教学重点:
会用三角板和量角器画角及尺规作图。
教学难点:
用直尺和圆规画一个角等于已知角。
教学过程:
预习导学:
在工程修建测量中,用到经纬仪,经纬仪是测量角的大小的仪器,还有其他度量角的工具吗?
用三角板画特殊角。
用一副三角板画出30°、45°、60°、90°的角。
能利用一副三角板画出15°、75°、105°、135°、165°的角吗?试一试。
分析:15°= + 75°= + 105°= +
135°= + 165°= + +
画出图形:
(3)用一副三角板可以画出 的角。
二、合作探究:
1、用量角器画出给定的角:
思考用量角器画角的步骤是什么?
用量角器画112°、76°的角。
用尺规画角。
教师演示:用无刻度的直尺和圆规画一个角等于已知角即∠AOB.
学生讨论:角的顶点和角的一边如何确定?角的另一边怎样画出?画图的关键是什么?
量一量,∠A'O'B'与∠AOB相等吗?
归纳作法:1、任画一条射线O'A';
2、以O为圆心,任意长为半径画弧,分别交OA、OB于点C、D;
3、以O'为圆心,OC长为半径画弧交O'A'于 C';
4、以C'为圆心,CD长为半径画弧与前弧交于D';
5、过D'作射线O'B';
∠A'O'B'就是所要求作的角。
说明:(1)在数学中,把只用直尺(无刻度的)和圆规画图称为尺规作图。
(2)在画图过程中画出的图形(点、线、弧线等),也叫作图痕迹,这些痕迹必须保留。
(3)图画好后,要写出画图结论。
三、课堂检测:
已知∠ABC,求作∠A'B'C',使∠A'B'C'=2∠ABC.
四、思维拓展:
如图,已知两个锐角、,其中2∠>∠,画一个角,使它等于2∠-∠
教学后记
4.3.2 角的比较与运算
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.会比较两个角的大小,能估计一个角的大小,在操作中认识角的平分线;
2.知道两个角的大小比较方法;
3.会进行有关角的计算.
教学重点:角的计算.
教学难点:角的识图.
教学过程:
一.预习导学:
1.怎样比较两条线段的长短?(口述)
2.类似地,如何比较两个角的大小呢?
与线段长短比较类似,我们可以用 量出角的度数,然后比较它们的大小;也可以把它们 在一起比较大小.
二.合作探究:
(一) 1.叠合法:从“形”的方面进行比较.
把两个角的顶点和一边分别重合,另外两条边落在重合边的同旁,通过另一边的位置关系比较大小.
学习课本P138,观察图4.3—6,讨论回答课本P 138思考问题.
2.度量法:从“数”的方面比较,分别量出每个角的度数.
归纳:
(1) 两个角的大小关系有 种;
(2) 角的 关系与角的 关系一致;
(3) 角的大小只与 有关,而与 无关,因为角的边是 而不是 .
3.角平分线:
如图1,如果∠AOB=∠BOC,那么∠AOC=2 =2 ,∠AOB= = . 像OB这样,从一个角的 出发,把这个角分成 的 .叫做这个角的平分线.
归纳:(1) 角的平分线是从角的顶点出发的一条 ;
(2) 这条射线把这个角分成 的角.
(二) 例题学习:
1.学习课本P140例1,回答下列问题:
分析:(1) AB是直线,所以AOB是 角,它是 度.
(2) ∠AOB=∠ +∠ ;∠BOC=∠ -∠ .
(3) 写出解答过程.
2.学习课本P140例2.
(三) 课堂训练:课本P140练习题1、2、3题.
(四) 课堂检测:
1.如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.
(1) 2∠BOC是哪个角? (2) ∠BOD是哪个角?
(3) ∠AOB+∠BOC等于哪个角?
(4) 求∠AOB和∠BOD的度数.
2.如图,将一副三角板叠放在一起,使直角顶点重合于O,求∠AOC+∠DOB的度数.
思维拓展:
如图,将一张长方形的纸斜折过去,使角顶点A落在A′处,BC为折痕,然后把BE边折过去,使之与A′B边重合,折痕为BD,那么两折痕BC、BD间的夹角是多少度?
教学后记:
4.3.3 余角和补角(一)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.掌握互为余角,互为补角的概念;
2.会正确表示一个角的余角或补角;
3.能熟练地求出一个角的余角或补角.
教学重点:互余、互补角的概念.
教学难点:互余和互补角的正确判断.
教学过程:
一.预习导学:
1.观察一副三角尺,你能说出每一个角的度数吗?在每一个三角尺中,两个锐角的和是多少度?
2.如图1、2,过平角∠AOB、直角∠COD作射线OM、ON,射线OM、ON把平角∠AOB、直角∠COD分别分成几个角?它们的度数关系如何?
二.合作探究:
1.学习课本P141内容,填空:
(1) 两个角的度数的和是90°,那么这两个角叫做 ,简称 ,即其中一个角是另一个角的 .
(2) 两个角的度数的和是180°,那么这两个角叫做 ,简称 ,即其中一个角是另一个角的 .
(3) 角α的余角可以表示为 ,补角可以表示为 .
温馨提示:(1) 互为余角,互为补角是指两个角而非一个角;
(2) 互为余角,互为补角与两个角所处的位置无关.
2.例题学习
学习课本P142例3,填空:
由∠1与∠2互补,可得∠2=180°- ;
由∠3与∠4互补,可得∠4=180°- ,因为∠1=∠3;所以 = .
归纳:等角的补角相等,等角的余角相等.
三.当堂训练:
1.课本P144第8题.
2.(1) 如果∠1+∠2=90°,∠2+∠3=90°,那么∠1与∠3的关系是 .
(2) 一个锐角的补角比这个角的余角大 .
(3) 若一个角的余角是这个角的,则这个角是 ,这个角的补角是 .
3.一个角的补角加上10°后等于这个角的余角的3倍,求这个角的度数.
四.课堂检测:
1.若两个角的和与两角的差之和等于1个平角的度数,则这两个角( )
A.一个是锐角,一个是钝角 B.都是钝角
C.必有一个是直角 D.两个都是直角
2.(1) 一个角的余角与补角也互为补角,这个角是 .
(2) 互为余角且相等的角是 ,互为补角且相等的角是 .
3.如图,AOE是一条直线,∠AOB=∠COD=90°,如果∠1=30°,那么∠2= ,∠3= . 和∠1互为余角的角有 ,和∠1相等的角有 .
五.思维拓展:
如图,∠AOB=90°,OM平分∠AOC、ON平分∠BOC. 求∠MON的度数.
教学后记:
4.3.3 余角和补角(二)
课型:新授课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:正确理解方位角,能画出方位角所表示方向的射线;
教学重点:画出方位角所表示方向的射线.
教学难点:能用方位角知识解决实际问题.
教学过程:
一.预习导学:
1.(1) 若∠1+∠2=90°,∠1+∠3=90°,则∠1与∠2是 关系,∠1与∠3是 关系,∠2与∠3是 关系,根据 .
(2) 若∠1+∠2=180°,∠3+∠4=180°,则∠1与∠2是 关系,∠3与∠4是 关系,∠2与∠3是 关系,根据 .
2.如图,在△ABC中,AC⊥BC,CD⊥AB于D,若已知∠1+∠3=90°,∠2+∠4=90°,且∠1+∠2=90°. 请指出图中所有相等的角.
二.合作探究:
1.在日常生活中,八个方向是不够用的,如果要准确表示方向,就要引导方位角的概念.
例如:OA表示北偏东30°方向的一条射线,仿照上述方向,你能表示下列方向吗?
(1) 南偏东60° ( )
(2) 北偏西60° ( )
(3) 东南方向 ( )
(4) 南北方向 ( )
(5) 东西方向 ( )
(6) 西南方向 ( )
注意:方位角的表示方法:先写南或北,再写偏东或偏西多少度.
2.例题学习:
学习课本P142例4,填空:
画法:找客轮B,以点 为顶点,表示 方向的射线为角的一边,画 的角,使它的另一边 落在东与北之间,射线OB的方向就是 ,即客轮B所在方向.请你在图中画出表示货轮C和海岛D方向的射线.
三.当堂训练:
1.课本P144第9题.
2.如图所示,射线OA表示的方向是 ,射线OB表示的方向是 ,射线OC表示的方向是 .
3.甲从O点出发,沿北偏西30°方向走了50米,到达A点,乙也从O点出发,沿南偏东35°方向走了80米到达B点. 求∠AOB.
四.课堂检测:
1.如图,指出OA是表示什么方向的一条射线?仿照这条射线画出表示下列方向的射线:
(1) 南偏东60°;(2) 北偏西70°;(3) 西南方向.
2.“海神”号货轮从A港出发,先沿东北方向(北偏东45°)行驶50km,再沿北偏西30°方向行驶35km,到达目的地. 问目的地在A港什么方向?
五.思维拓展:
如图,小华有一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,现在知道C地在A地的北偏东30°,在B地南偏东45°,你能帮小华确定C地的位置吗?
教学后记:
第四章 小结
课型:复习课 主备:方方 审核:七年级数学备课组
班级: 姓名:
教学目标:
1.复习几何图形中有关概念;
2.本章基础知识运用.
教学过程:
一.完成知识图解(学生自学)
二.知识点应用:
1.填空:(1) 圆柱的底面是 ,侧面是 ,展开后的侧面是 .
(2) 棱柱的侧面是 ,分为 棱柱和 棱柱;圆可以分割成 个扇形.
(3) 如图是一个正方体展开图,将它折叠成正方体后,“建”字对面是 .
(4) 两根木条,一根长60cm,一根长100cm,将它们的一端重合,顺次放在同一条直线上,此时两根木条的中点间的距离是 cm.
(5) 已知∠α=37°25′,∠β=52°48′,则∠α+∠β= .
(6) 1.36°= ° ′ ″
(7) 已知∠α的余角是50°,则∠α的补角的度数是 .
2.计算:(1) 把角度9.03°化为度、分、秒,再求它们的余角和补角.
(2) 如图,点O在直线AC上,OD平分∠AOB,∠EOC=2∠BOE,∠DOE=72°,求∠EOC.
三.课堂检测:
1.(1)23°45′+24°15′ (2) 23°53′×3+107°43′÷5
2.一个角的余角比它的补角的少20°,求这个角.
3.如图,∠AOB=79°,∠DOC=25°,OD平分∠AOC.
求∠BOC的度数.
四.探索题:如图,OA的方向是北偏东15°,OB的方向是北偏西30°.
(1) 若∠AOC=∠AOB,则OC的方向是 .
(2) OD是OB的反向延长线,OD的方向是 .
(3) ∠BOD可看做是OB绕O逆时针方向旋转至OD,作∠BOD的平分线OE,并用方位角表示OE的方向.
(4) 在(1) (2) (3)的条件下,求∠COE.
教学后记:
第四章 单元检测
(满分:100分) 姓名______________
一、选择题(每小题3分,共18分)
1.下列说法正确的是( )
A.直线AB和直线BA是两条直线; B.射线AB和射线BA是两条射线;
C.线段AB和线段BA是两条线段; D.直线AB和直线a不能是同一条直线。
2.下列图中角的表示方法正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.下面图形经过折叠可以围成一个棱柱的是( )
A. B.
D.
4.将如图所示的正方体沿某些棱展开后,能得到的图形是( )
A. B. C. D.
5.若∠A = 20°18′,∠B = 20°15′30″,∠C = 20.25°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
6.经过任意三点中的两点共可画出( )
A.1条直线 B.2条直线 C.1条或3条直线 D.3条直线
二、填空题(每小题3分,共12分)
7.有公共顶点的两条射线分别表示南偏15°与北偏东25°,则这两条射线组成的角的度数为_____________________.
8.如图,若CB = 4 cm,DB = 7 cm,且D是AC的中点,则AC =_________________.
9.八时三十分,时针与分针夹角度数是_______.
10.如图,从学校A到书店B最近的路线是①号路线,其道理用几何知识解释应是_____________________________________.
三、解答题(每小题10分,共30分) 11.计算:
12.一个角的余角比它的补角的还少40°,求这个角。
13.如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数。
(填空10 )
四、试一试,探一探(每小题20分)
14.如图,BO、CO分别平分∠ABC和∠ACB,
(1)若∠A = 60°,求∠O; (2)若∠A =100°、120°,∠O又是多少?
(3)由(1)、(2)你又发现了什么规律?当∠A的度数发生变化后,你的结论仍成立吗? (提示:三角形的内角和等于180°)
15.如图,点C在线段AB上,AC = 8 cm,CB = 6 cm,点M、N分别是AC、BC的中点。
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC + CB = a cm,其它条件不变,你能猜想MN的长度吗?并说明理由。你能用一句简洁的话描述你发现的结论吗?
(3)若C在线段AB的延长线上,且满足ACBC = b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由。
第四章单元测验试题
姓名 班别 成绩
一、填空题(第2题1分一空,其余2分一空,共32分)
1、已知线段AB=8cm,延长AB至C,使AC=2AB,D是AB中点,则线段CD=____ __.
2、57.32°=_______°_______′_______″;27°14′24″=___ __°.
4、已知∠a=36°42′15″,那么∠a的余角等于________.
5、∠1+∠2=180°,∠2+∠3=180°,根据___ __ ___,得∠1=∠3.
6、102°43′32″+77°16′28″=_____ ___;98°12′25″÷5=___ __.
7、如图是某些几何体的表面展开图,则这些几何体分别是
图1:
图2:
图3:
8、若要使图中平面展开图按虚线折叠成正方体后,相对面上
两个数之和为6,x=_ ___,y=______.
9、要在墙上固定一根木条,至少要 个钉子,
根据的原理是 。
10、不在同一直线上的四点最多能确定????????? 条直线。
11、小明每天下午5:30回家,这时分针与时针所成的角的度数为___________。
二、选择题(3分一题、共36分)
1.如图1所示的棱柱有( )
A.4个面 B.6个面 C.12条棱 D.15条棱
2.如图2,从正面看可看到△的是( )
3.下列语句正确的是( )
A.如果PA=PB,那么P是线段AB的中点; B.作∠AOB的平分线CD
C.连接A、B两点得直线AB; D.反向延长射线OP(O为端点)
4. 对于直线,线段,射线,在下列各图中能相交的是(?????? )
5.如果与互补,与互余,则与的关系是(?????? )
(A)= (B) (C) (D)以上都不对
6.下列四个图中,能用∠1、∠AOB、∠O三种方法表示同一个的是(??? )
?
?
?
7.如图,,,点B、O、D在同一直线上,则的度数(????? )
(A) (B) (C) (D)
8.下列图中角的表示方法正确的个数有( )
(A)1个 (B)2个 (C)3个 (D)4个
9.如图的几何体,左视图是 ( )
10.下列叙述正确的是(???? )
?A.180°的角是补角????????B.110°和90°的角互为补角
C.10°、20°、60°的角互为余角? D.120°和60°的角互为补角
11.如图,点A位于点O的 方向上.( ).
(A)南偏东35° (B)北偏西65° (C)南偏东65° (D)南偏西65°
12. 将下列图形绕直线l旋转一周, 可以得到右图所示的立体图形的是( )
三、作图题
1.根据下列要求画图:(6分)
(1)连接线段AB;(2)画射线OA,射线OB;
(3)在线段AB上取一点C,在射线OA上取一
点D(点C、D不与点A重合),画直线CD,使
直线CD与射线OB交于点E。
2. 用尺规画出下列图形:已知、、()
求作线段AB使AB=。(不要求写画法)?(6分)
?
?
四、解答题
1.如图,D是AB的中点, E是BC的中点,BE=AC=2cm,线段DE的长,
求线段DE的长. (5分)
2.如图,点A、O、E在同一直线上,∠AOB=40°,∠EOD=28°46’,OD平分∠COE,
求∠COB的度数(5分)
B C
D
A O E
3.一个角的补角与它的余角的度数的3倍,求这个角的度数.(5分)
解:设这个角为,则它的补角为 ,余角为 ,依题意得
4.如图,∠AOD=∠BOC=90°,∠COD=42°,求∠AOC、∠AOB的度数. (5分)
3.如下图,在已知角内画射线,画1条射线,图中共有 个角;画2条射线,图中共有 个角;画3条射线,图中共有 个角,
求画n条射线所得的角的个数。(9分)
