人教版五年级下学期数学4.4.1最大公因数课件(共20张PPT)
文档属性
| 名称 | 人教版五年级下学期数学4.4.1最大公因数课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 15:34:11 | ||
图片预览






文档简介
(共20张PPT)
最大公因数
学习目标
经历探究求两个数最大公因数方法的过程,培养学生分析、归纳等思维能力。激发学生自主学习、积极探索和合作交流的良好习惯。
掌握求两个数最大公因数的方法,会选择合适的方法正确的求两个数的最大公因数。能初步应用求最大公因数的方法解决生活中的简单实际问题;
理解公因数和最大公因数的意义,理解因数、公因数和最大公因数的区别和联系;
【重点】
掌握运用公因数的知识解决生活中简单的实际问题的方法。
【难点】
能正确判断生活中的实际问题是否要利用最大公因数的知识来解决。
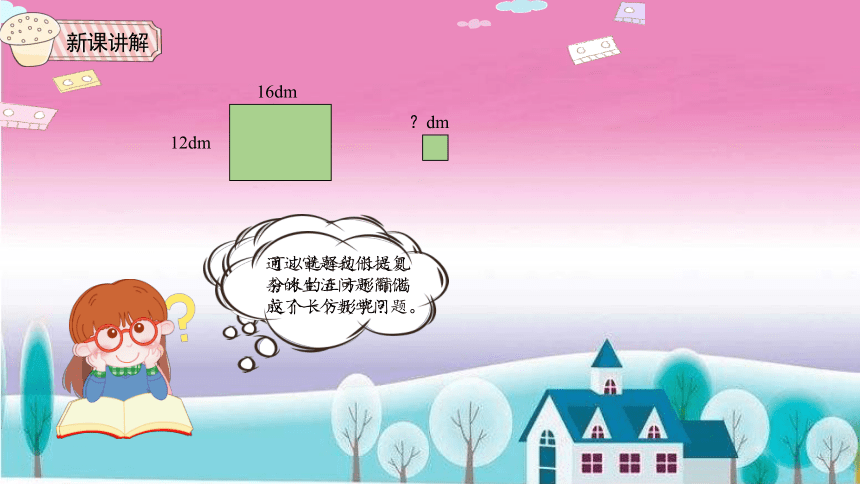
新课讲解
16dm
12dm
?dm
正方形的边长是整分米数是什么意思?
图中还有有价值的信息吗?
通过审题我们把复杂的生活问题简化成了一个数学问题。
可以选择边长是几分米的正方形铺满这个长方形呢?
小组讨论:观察两个数的公因数和它
们的最大公因数之间有什么关系?
最大公因数是所有公因数的倍数。
新课讲解
小结
1,2,4既是8的因数又是12的因数,那我们就把它们叫作8和12的公因数。
8的因数
12的因数
8
4
2,
3,6,12
1,
8和12的公因数
分析与解答
16的因数有:1, 2, 4, 8, 16
12的因数有:1, 2, 3, 4, 6, 12
12和16的公因数有:1, 2, 4。最大公因数是4。
所以,可以选边长是1dm、2dm、4dm的地砖,边长最大是4dm。
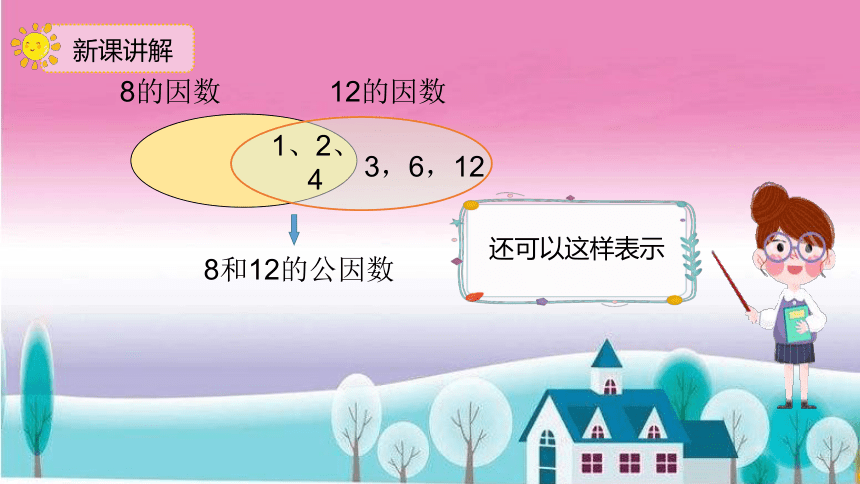
新课讲解
8的因数
12的因数
8
3,6,12
1、2、4
8和12的公因数
还可以这样表示
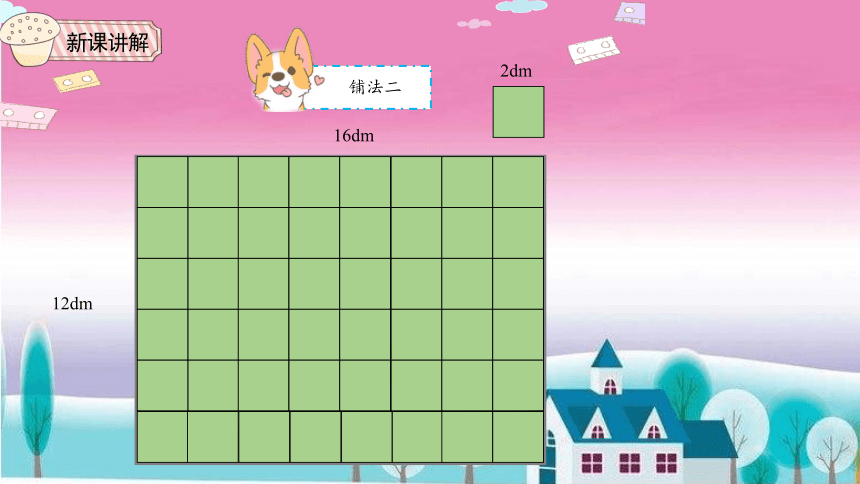
新课讲解
铺法二
12dm
2dm
16dm
有两根木料,一根长8米,另一根长6米,现在要把它们截成相等的小段,每根不准有剩余,每小段最长
是多少?一共可以截成多少段?
8 6
2
4
3
8米
2米
2米
2米
2米
6米
2米
2米
2米
列举法:
8的因数:1、2、4、8
6的因数:1、2、3、6
6和8的最大公因数:2
8÷2=4(段)
6÷2=3(段)
4+3=7(段)
短除法:
新课讲解
回顾我们解决这个问题的过程,你有哪些收获?
判断。(对的画“√”,错的画“×”)
(1)两个数的公因数的个数是无限的。( )
(2)5和7没有公因数。( )
(3)两个合数的最大公因数可能是1。( )
易错辨析
辨析:公因数的个数是有限的。
辨析:忽视了公因数1。
新课讲解
①枚举法:
18的因数:1,2,3,6,9,18
27的因数:1,3,9,27
18和27的公因数:1,3,9
最大公因数
课堂练习
把6和24的因数、公因数分别填在相应的位置,再圈出它们的最大公因数。
6的因数
24的因数
1、2、
3、6
1、2、3、
4、6、8、12、
24
知识运用
在18的因数上画“○”,在30的因数上画“□”。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
根据上表按要求把数填在下面的集合圈内。
18
1
2
3
6
5
10
15
30
18和30的最大公因数是 。
6
18的因数
30的因数
18和30的公因数
9
男、女生分别站成若干排,要使每排的人数相同,每排最多有多少人 这时男、女生分别有几排
规范解答
36
48
2
2
18
24
9
12
3
3
4
36和48的最大公因数是2×2×3=12。
男生:48÷12=4(排)
女生:36÷12=3(排)
答:每排最多有12人,这时男生有4排,女生有3排。
(教材第63页第6题)
课堂小结
12cm
6cm
一张长96cm,宽60cm的长方形里剪出若干个边长相等的正方形,正方形边长最大可以是 .
12cm
回顾小结
在铺地砖问题中,要使地面铺满且使用的地砖都是整块,就是求长和宽的公因数;求地砖的边长最大是多少,就是求长和宽的最大公因数。
当所求量分别与两个(或几个)已知量的因数有关时,可以用公因数或最大公因数的知识解决。
1、课后练习P 61第3 题;
2、练习册P38.
课后作业
聪明出于勤奋,天才在于积累。
最大公因数
学习目标
经历探究求两个数最大公因数方法的过程,培养学生分析、归纳等思维能力。激发学生自主学习、积极探索和合作交流的良好习惯。
掌握求两个数最大公因数的方法,会选择合适的方法正确的求两个数的最大公因数。能初步应用求最大公因数的方法解决生活中的简单实际问题;
理解公因数和最大公因数的意义,理解因数、公因数和最大公因数的区别和联系;
【重点】
掌握运用公因数的知识解决生活中简单的实际问题的方法。
【难点】
能正确判断生活中的实际问题是否要利用最大公因数的知识来解决。
新课讲解
16dm
12dm
?dm
正方形的边长是整分米数是什么意思?
图中还有有价值的信息吗?
通过审题我们把复杂的生活问题简化成了一个数学问题。
可以选择边长是几分米的正方形铺满这个长方形呢?
小组讨论:观察两个数的公因数和它
们的最大公因数之间有什么关系?
最大公因数是所有公因数的倍数。
新课讲解
小结
1,2,4既是8的因数又是12的因数,那我们就把它们叫作8和12的公因数。
8的因数
12的因数
8
4
2,
3,6,12
1,
8和12的公因数
分析与解答
16的因数有:1, 2, 4, 8, 16
12的因数有:1, 2, 3, 4, 6, 12
12和16的公因数有:1, 2, 4。最大公因数是4。
所以,可以选边长是1dm、2dm、4dm的地砖,边长最大是4dm。
新课讲解
8的因数
12的因数
8
3,6,12
1、2、4
8和12的公因数
还可以这样表示
新课讲解
铺法二
12dm
2dm
16dm
有两根木料,一根长8米,另一根长6米,现在要把它们截成相等的小段,每根不准有剩余,每小段最长
是多少?一共可以截成多少段?
8 6
2
4
3
8米
2米
2米
2米
2米
6米
2米
2米
2米
列举法:
8的因数:1、2、4、8
6的因数:1、2、3、6
6和8的最大公因数:2
8÷2=4(段)
6÷2=3(段)
4+3=7(段)
短除法:
新课讲解
回顾我们解决这个问题的过程,你有哪些收获?
判断。(对的画“√”,错的画“×”)
(1)两个数的公因数的个数是无限的。( )
(2)5和7没有公因数。( )
(3)两个合数的最大公因数可能是1。( )
易错辨析
辨析:公因数的个数是有限的。
辨析:忽视了公因数1。
新课讲解
①枚举法:
18的因数:1,2,3,6,9,18
27的因数:1,3,9,27
18和27的公因数:1,3,9
最大公因数
课堂练习
把6和24的因数、公因数分别填在相应的位置,再圈出它们的最大公因数。
6的因数
24的因数
1、2、
3、6
1、2、3、
4、6、8、12、
24
知识运用
在18的因数上画“○”,在30的因数上画“□”。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
根据上表按要求把数填在下面的集合圈内。
18
1
2
3
6
5
10
15
30
18和30的最大公因数是 。
6
18的因数
30的因数
18和30的公因数
9
男、女生分别站成若干排,要使每排的人数相同,每排最多有多少人 这时男、女生分别有几排
规范解答
36
48
2
2
18
24
9
12
3
3
4
36和48的最大公因数是2×2×3=12。
男生:48÷12=4(排)
女生:36÷12=3(排)
答:每排最多有12人,这时男生有4排,女生有3排。
(教材第63页第6题)
课堂小结
12cm
6cm
一张长96cm,宽60cm的长方形里剪出若干个边长相等的正方形,正方形边长最大可以是 .
12cm
回顾小结
在铺地砖问题中,要使地面铺满且使用的地砖都是整块,就是求长和宽的公因数;求地砖的边长最大是多少,就是求长和宽的最大公因数。
当所求量分别与两个(或几个)已知量的因数有关时,可以用公因数或最大公因数的知识解决。
1、课后练习P 61第3 题;
2、练习册P38.
课后作业
聪明出于勤奋,天才在于积累。
