北师大版九年级下册2.4.1二次函数的应用——最大(小)面积问题 学案(无答案)
文档属性
| 名称 | 北师大版九年级下册2.4.1二次函数的应用——最大(小)面积问题 学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 48.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 14:08:22 | ||
图片预览

文档简介
2.4.1二次函数的应用——最大(小)面积问题
【学习目标】
能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题中的最大(小)值.
【学习方法】自主探究与小组合作交流相结合.
【学习重点】:能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题.
【学习难点】:能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能运用二次函数的有关知识解决最大(小)面积问题.
【学习过程】
一、预学:
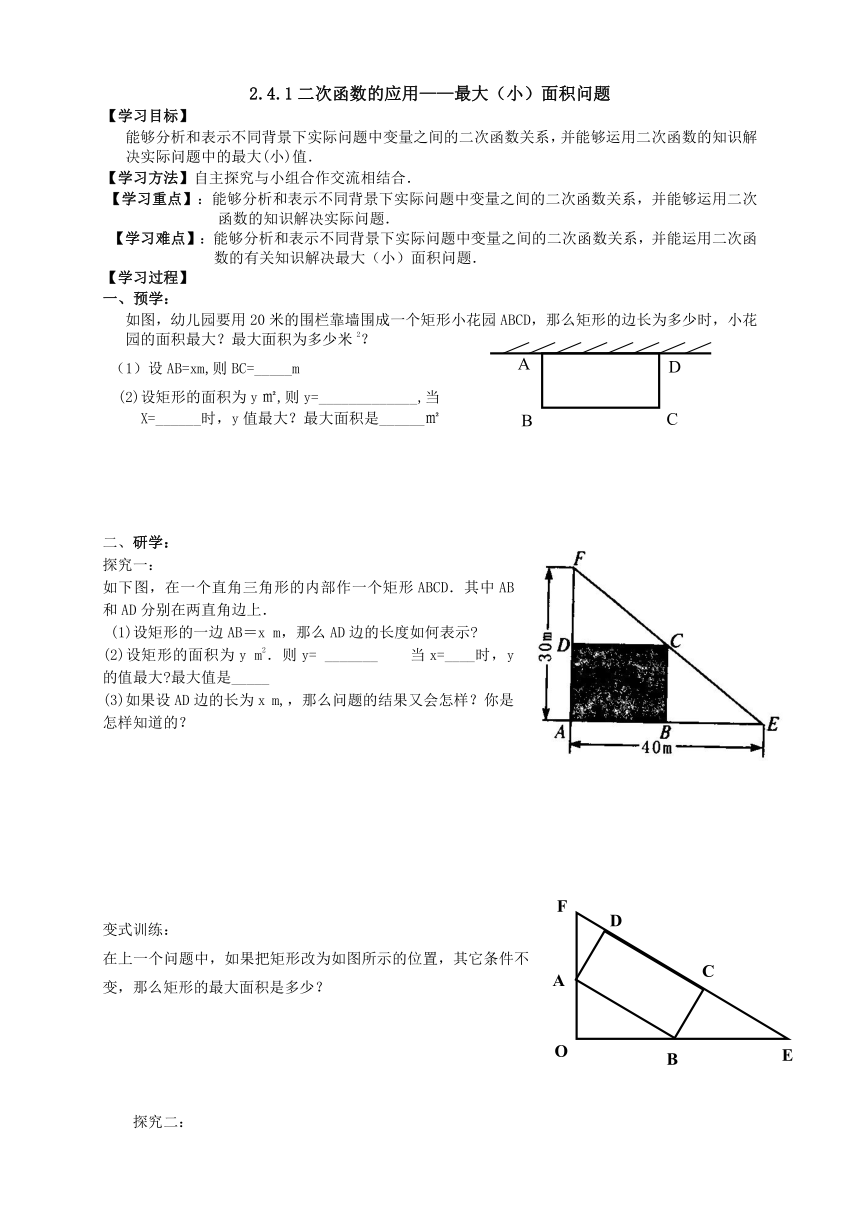
如图,幼儿园要用20米的围栏靠墙围成一个矩形小花园ABCD,那么矩形的边长为多少时,小花园的面积最大?最大面积为多少米2?
(1)设AB=xm,则BC=_____m
(2)设矩形的面积为y㎡,则y=_____________,当
X=______时,y值最大?最大面积是______㎡
二、研学:
探究一:
如下图,在一个直角三角形的内部作一个矩形ABCD.其中AB和AD分别在两直角边上.
(1)设矩形的一边AB=x m,那么AD边的长度如何表示
(2)设矩形的面积为y m2.则y= _______ 当x=____时,y的值最大 最大值是_____
(3)如果设AD边的长为x m,,那么问题的结果又会怎样?你是怎样知道的?
变式训练:
在上一个问题中,如果把矩形改为如图所示的位置,其它条件不变,那么矩形的最大面积是多少?
探究二:
某建筑物的窗户如下图所示,它的上半部是半圆,下半部是矩形,制
造窗框的材料总长(图中所有黑线的长度和)为15 m,当x等于多少时,窗
户通过的光线最多(结果精确到0.01 m) 此时,窗户的面积是多少
三、评学:
【积累巩固】
1、 矩形的一边长为x,周长为8,则当矩形面积最大时x的值为( )
A 4 B 2 C 6 D 5
2.一个菱形的对角线之和为20,则其最大面积为_________.
3.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做一个正方形,则这两个正方形面积之和的最小值是_____c㎡
4.如图所示△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成一个矩形零件,是矩形的一边在BC上,其余两个顶点在AB、AC上,该矩形的长QM=y(mm),宽MN=x(mm).
(1)如何用含x的代数式表示y
(2)当x与y分别取什么值时,矩形PQMN的面积最大?最大面积是多少?
【拓展延伸】
在矩形ABCD中,AB=6,BC=12,点P从点A出发沿AB边向点B以1/秒的速度移动,同时点Q从点B出发沿BC边向点C以2/秒的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,设运动时间为t秒(0(1)运动开始后第几秒时,△PBQ的面积等于8;
(2)设五边形APQCD的面积为S,写出S与t的函数关系式,
t为何值时S最小?
求出S的最小值.
【课堂小结】
求实际背景最值问题的方法是:设法把关于最值的问题转化为二次函数最值的方法进行求解。
B
D
A
C
A
B
C
D
F
O
E
A
B
C
QE
MF
NG
P
D
E
A
B
C
D
P
Q
【学习目标】
能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题中的最大(小)值.
【学习方法】自主探究与小组合作交流相结合.
【学习重点】:能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能够运用二次函数的知识解决实际问题.
【学习难点】:能够分析和表示不同背景下实际问题中变量之间的二次函数关系,并能运用二次函数的有关知识解决最大(小)面积问题.
【学习过程】
一、预学:
如图,幼儿园要用20米的围栏靠墙围成一个矩形小花园ABCD,那么矩形的边长为多少时,小花园的面积最大?最大面积为多少米2?
(1)设AB=xm,则BC=_____m
(2)设矩形的面积为y㎡,则y=_____________,当
X=______时,y值最大?最大面积是______㎡
二、研学:
探究一:
如下图,在一个直角三角形的内部作一个矩形ABCD.其中AB和AD分别在两直角边上.
(1)设矩形的一边AB=x m,那么AD边的长度如何表示
(2)设矩形的面积为y m2.则y= _______ 当x=____时,y的值最大 最大值是_____
(3)如果设AD边的长为x m,,那么问题的结果又会怎样?你是怎样知道的?
变式训练:
在上一个问题中,如果把矩形改为如图所示的位置,其它条件不变,那么矩形的最大面积是多少?
探究二:
某建筑物的窗户如下图所示,它的上半部是半圆,下半部是矩形,制
造窗框的材料总长(图中所有黑线的长度和)为15 m,当x等于多少时,窗
户通过的光线最多(结果精确到0.01 m) 此时,窗户的面积是多少
三、评学:
【积累巩固】
1、 矩形的一边长为x,周长为8,则当矩形面积最大时x的值为( )
A 4 B 2 C 6 D 5
2.一个菱形的对角线之和为20,则其最大面积为_________.
3.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做一个正方形,则这两个正方形面积之和的最小值是_____c㎡
4.如图所示△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成一个矩形零件,是矩形的一边在BC上,其余两个顶点在AB、AC上,该矩形的长QM=y(mm),宽MN=x(mm).
(1)如何用含x的代数式表示y
(2)当x与y分别取什么值时,矩形PQMN的面积最大?最大面积是多少?
【拓展延伸】
在矩形ABCD中,AB=6,BC=12,点P从点A出发沿AB边向点B以1/秒的速度移动,同时点Q从点B出发沿BC边向点C以2/秒的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动,设运动时间为t秒(0
(2)设五边形APQCD的面积为S,写出S与t的函数关系式,
t为何值时S最小?
求出S的最小值.
【课堂小结】
求实际背景最值问题的方法是:设法把关于最值的问题转化为二次函数最值的方法进行求解。
B
D
A
C
A
B
C
D
F
O
E
A
B
C
QE
MF
NG
P
D
E
A
B
C
D
P
Q
