北师大版九年级下册2.2.3 二次函数的图象与性质 学案(无答案)
文档属性
| 名称 | 北师大版九年级下册2.2.3 二次函数的图象与性质 学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 80.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 14:14:10 | ||
图片预览

文档简介
2.2.3 二次函数的图象与性质
【学习目标】: 1.使学生会用描点法画二次函数y=a(x+h)2 和y=a(x-h)2 和y=a(x-h)2+k(a≠0)的图象.
2. 使学生能根据图象认识和理解二次函数的性质,说出二次函数的开口方向、对称轴和顶点坐标.
【学习重点】:会用描点法画二次函数 y=a(x+h) 和y=a(x-h) (a≠0)y=a(x-h) +k(a≠0)的图象,掌握它的性质.
【学习难点】:渗透数形结合思想
【学习过程】:
一、预学:
1 提出问题,创设情景:
在同一直角坐标系中作出下列二次函数的图象
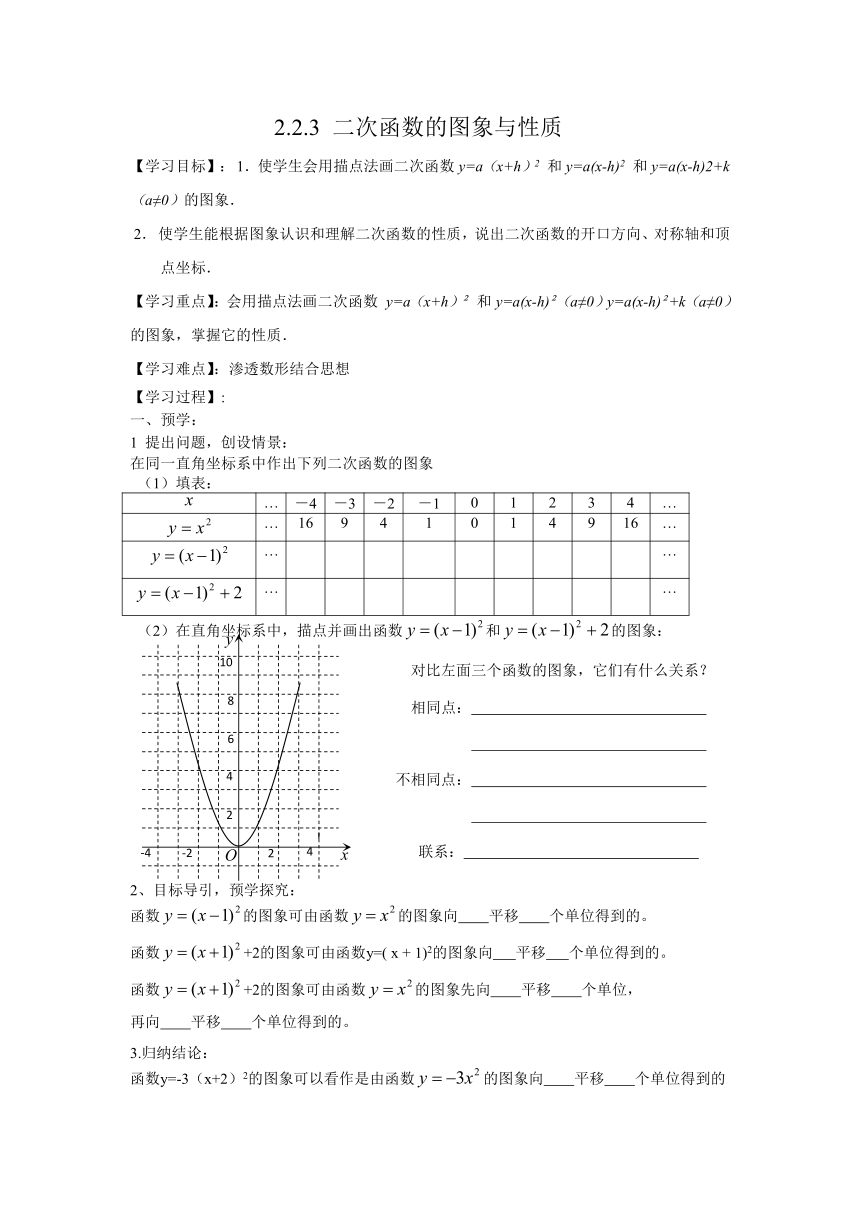
(1)填表:
… -4 -3 -2 -1 0 1 2 3 4 …
… 16 9 4 1 0 1 4 9 16 …
… …
… …
(2)在直角坐标系中,描点并画出函数和的图象:
对比左面三个函数的图象,它们有什么关系?
相同点:
不相同点:
联系:
2、目标导引,预学探究:
函数的图象可由函数的图象向 平移 个单位得到的。
函数+2的图象可由函数y=( x + 1)2的图象向 平移 个单位得到的。
函数+2的图象可由函数的图象先向 平移 个单位,
再向 平移 个单位得到的。
3.归纳结论:
函数y=-3(x+2)2的图象可以看作是由函数的图象向 平移 个单位得到的
函数y=-3(x+2)2-4的图象可以看作是由函数的图象
得到的。
二、研学(合作发现,交流展示)
探究一:
平移规律:____________________________,
函数 的图象可由的图象向 平移 个单位得到。
函数的图象可由的图象向 平移 个单位得到。
函数的图象可由的图象先向 平移 个单位再向 平移 个单位得到
探究二:y=2x2向下平移5个单位,所得函数的解析式为 ,
y=2x2向左平移5个单位,所得函数的解析式为 ,
y=2x2先向上平移5个单位,再向右平移2个单位,所得函数的解析式为 ,
y=2(x-7)2向左平移5个单位,所得函数的解析式为 ,
三、评学:积累巩固:
1抛物线的开口______,对称轴是________,顶点坐标是________,
它可以看作是由抛物线____________向____平移_____个单位长度得到的
2函数的开口______,对称轴是________,顶点坐标是________,
它可以看作是由抛物线____________向____平移_____个单位长度得到的
3若函数的图象是由函数的图象向右平移个单位长度得到的,则
4把抛物线向上平移1个单位,再向左平移2个单位,得到的抛物线是( )
A. B.
5把向上平移2个单位,再向右平移1个单位,得到的抛物线是( )
A. B.
6抛物线的顶点坐标是 ( )
A.(1,2) B.(-1,2) C.(2,-1) D.(2,1)
拓展延伸:1一个二次函数的图象向下平移3个单位长度再向左平移2个单位后,得到二次函数y=的图象,试写出原二次函数的表达式.
2一条抛物线其形状、开口方向与抛物线相同,对称轴与抛物线相同,且顶点的纵坐标是3,则这条抛物线的函数解析式是_______________.
3已知抛物线与的开口方向和形状都相同,最低的坐标是(―2,―1).求的解析式,并说明抛物线是怎样由平移得到的;
课堂小结:
通过本课学习,你掌握了那些知识?获得了那些技能?还存在什么疑问?
【学习目标】: 1.使学生会用描点法画二次函数y=a(x+h)2 和y=a(x-h)2 和y=a(x-h)2+k(a≠0)的图象.
2. 使学生能根据图象认识和理解二次函数的性质,说出二次函数的开口方向、对称轴和顶点坐标.
【学习重点】:会用描点法画二次函数 y=a(x+h) 和y=a(x-h) (a≠0)y=a(x-h) +k(a≠0)的图象,掌握它的性质.
【学习难点】:渗透数形结合思想
【学习过程】:
一、预学:
1 提出问题,创设情景:
在同一直角坐标系中作出下列二次函数的图象
(1)填表:
… -4 -3 -2 -1 0 1 2 3 4 …
… 16 9 4 1 0 1 4 9 16 …
… …
… …
(2)在直角坐标系中,描点并画出函数和的图象:
对比左面三个函数的图象,它们有什么关系?
相同点:
不相同点:
联系:
2、目标导引,预学探究:
函数的图象可由函数的图象向 平移 个单位得到的。
函数+2的图象可由函数y=( x + 1)2的图象向 平移 个单位得到的。
函数+2的图象可由函数的图象先向 平移 个单位,
再向 平移 个单位得到的。
3.归纳结论:
函数y=-3(x+2)2的图象可以看作是由函数的图象向 平移 个单位得到的
函数y=-3(x+2)2-4的图象可以看作是由函数的图象
得到的。
二、研学(合作发现,交流展示)
探究一:
平移规律:____________________________,
函数 的图象可由的图象向 平移 个单位得到。
函数的图象可由的图象向 平移 个单位得到。
函数的图象可由的图象先向 平移 个单位再向 平移 个单位得到
探究二:y=2x2向下平移5个单位,所得函数的解析式为 ,
y=2x2向左平移5个单位,所得函数的解析式为 ,
y=2x2先向上平移5个单位,再向右平移2个单位,所得函数的解析式为 ,
y=2(x-7)2向左平移5个单位,所得函数的解析式为 ,
三、评学:积累巩固:
1抛物线的开口______,对称轴是________,顶点坐标是________,
它可以看作是由抛物线____________向____平移_____个单位长度得到的
2函数的开口______,对称轴是________,顶点坐标是________,
它可以看作是由抛物线____________向____平移_____个单位长度得到的
3若函数的图象是由函数的图象向右平移个单位长度得到的,则
4把抛物线向上平移1个单位,再向左平移2个单位,得到的抛物线是( )
A. B.
5把向上平移2个单位,再向右平移1个单位,得到的抛物线是( )
A. B.
6抛物线的顶点坐标是 ( )
A.(1,2) B.(-1,2) C.(2,-1) D.(2,1)
拓展延伸:1一个二次函数的图象向下平移3个单位长度再向左平移2个单位后,得到二次函数y=的图象,试写出原二次函数的表达式.
2一条抛物线其形状、开口方向与抛物线相同,对称轴与抛物线相同,且顶点的纵坐标是3,则这条抛物线的函数解析式是_______________.
3已知抛物线与的开口方向和形状都相同,最低的坐标是(―2,―1).求的解析式,并说明抛物线是怎样由平移得到的;
课堂小结:
通过本课学习,你掌握了那些知识?获得了那些技能?还存在什么疑问?
