直线和圆的位置关系 切线的判定

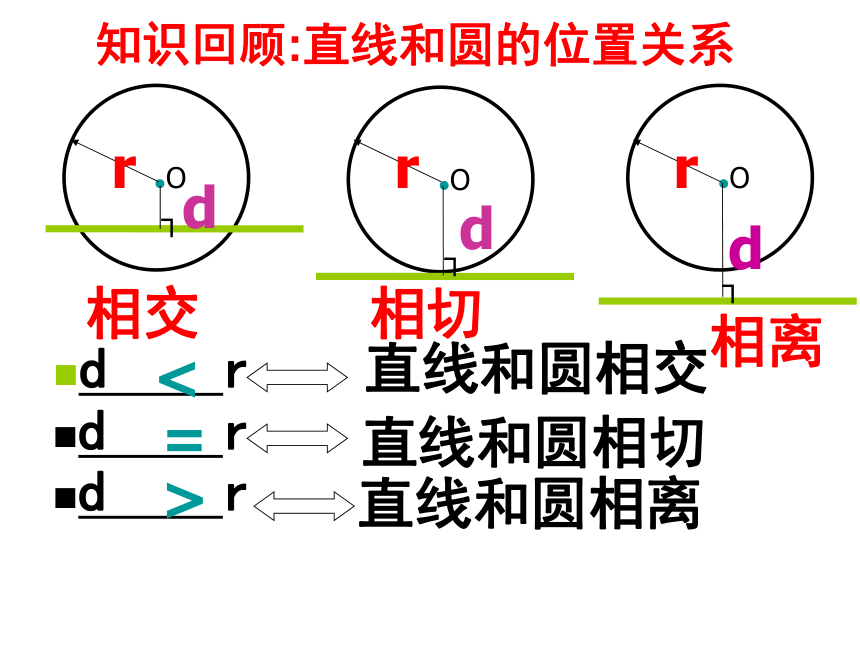
课件20张PPT。4.4直线与圆的位置关系(2)切线的判定定理及应用直线和圆相交d rd r　直线和圆相切直线和圆相离d r●O相交相切　相离┐dd┐d┐<=>知识回顾:直线和圆的位置关系 下雨天转动雨伞时飞出的水，以及在砂轮上打磨工件飞出的火星，均沿着圆的切线的方向飞出． 问一问:
1、当你在下雨天快速转动雨伞时水飞出的方向是什么方向？
2、砂轮打磨工件飞出火星的方向是什么方向？议一议请按照下述步骤作图:
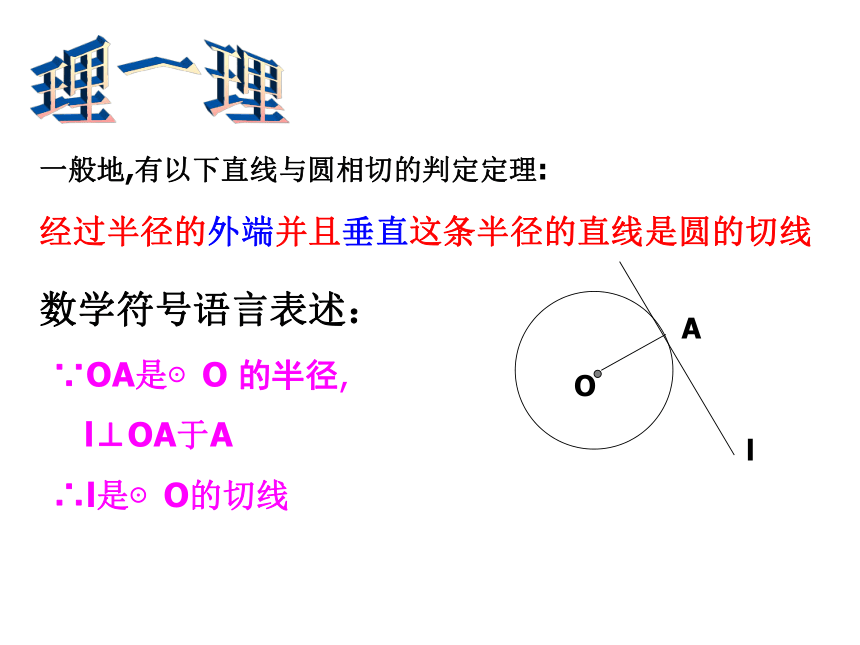
如图,在⊙O上任取一点A,连结OA,过点A作直线l⊥OA,OA思考以下问题:
(1)圆心O到直线l的距离和圆的半径有什么关系?(2)直线l和⊙O的位置有什么关系?根据什么?(3)由此你发现了什么?相等d=r相切特征一：直线L经过半径OA的外端点A特征二：直线L垂直于半径OA（直线l成为切线必须满足哪些特征？）理一理一般地,有以下直线与圆相切的判定定理:经过半径的外端并且垂直这条半径的直线是圆的切线OAl
∵OA是⊙O 的半径,
l⊥OA于A
∴l是⊙O的切线数学符号语言表述：
经过半径的外端并且垂直于这条半径的直线是圆的切线。判断下图中的l 是否为⊙O的切线⑴不是半径⑵不经过半径外端⑶与半径不垂直记一记：应用定理证明一条直线为圆的切线时，必须两个条件缺一不可：
①过半径外端
②垂直于这条半径。直线与圆相切的判定定理:想一想：判断一条直线是圆的切线，你现在会有多少种方法?有以下三种方法:
1.利用切线的定义:与圆有唯一公共点的直线是圆的切线。
2.利用d与r的关系作判断:当d＝r时直线是圆的切线。
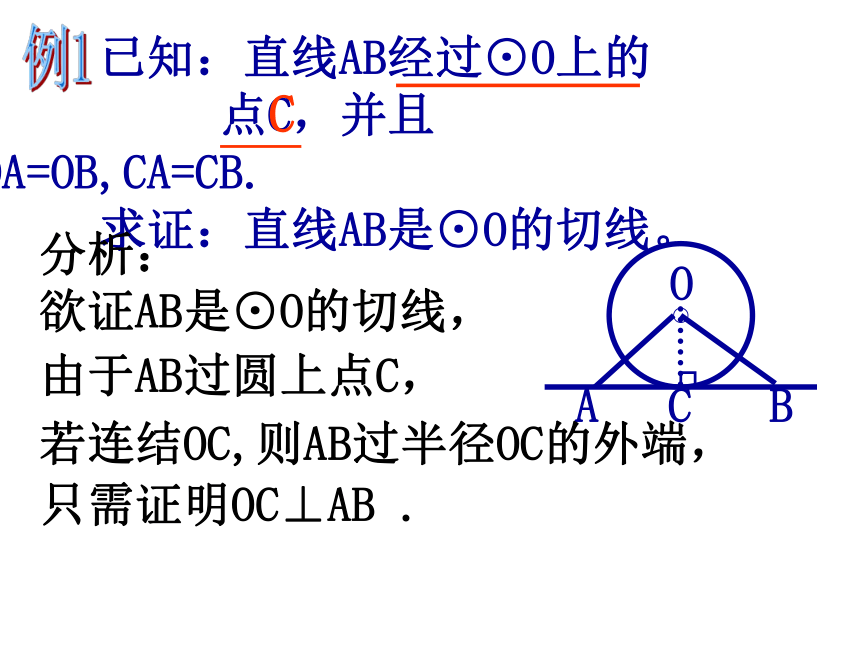
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。想一想练一练 1、如图，已知点B在⊙O上。根据下列条件，能否判定直线AB和⊙O相切？⑴OB=6,AO=10,AB=8？（2）若OB=OA, ∠ A=45° 已知：直线AB经过⊙O上的
点C，并且OA=OB,CA=CB.
求证：直线AB是⊙O的切线。OABC例1C分析：
欲证AB是⊙O的切线，由于AB过圆上点C，若连结OC,则AB过半径OC的外端，只需证明OC⊥AB .例1 已知：直线AB经过⊙O上的点C，并且OA=OB，CA＝CB．
求证：直线AB是⊙O的切线 分析：欲证AB是⊙O的切线．由于AB过圆上点C，若连结OC，则AB过半径OC的外端，只需证明OC⊥OB.
证明：连结0C
∵0A＝0B，CA＝CB，
∴0C是等腰三角形0AB底边AB上的中线．
∴AB⊥OC．
直线AB经过半径0C的外端C ,并且垂直于半径0C，
所以AB是⊙O的切线．例题评析已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30°.求证:直线AB是⊙O的切线ABCO证明：连结OB∵OB=OC，AB=BC，∠A=30°∴∠OBC=∠C=∠A=30°∴∠AOB=∠C+ ∠OBC =60°∴∠ABO=180°-（∠AOB+∠A）
=180°-（60°+30°）
=90°∴AB⊥OB∴AB为⊙O的切线一般情况下，要证明一条直线为圆的切线，它过半径外端（即一点已在圆上）是已知给出时，连半径，后只需证明直线垂直于这条半径。做一做已知O为∠BAC平分线上一点，OD⊥AB于D，以O为圆心，OD为半径作圆O，求证：⊙O与AC相切例2：DCABO∟分析:欲证直线与圆相切，
但直线与圆的交点不明确时，
往往过圆心作这条直线的垂线段，
再证明d=r即可
E证明：过O作OE⊥AC于E。
∵ AO平分∠BAC，OD⊥AB
∴ OE＝OD
∵ OD是⊙O的半径
∴ AC是⊙O的切线。
小 结 例1与例2的证法有何不同?
(1)如果直线与圆的交点明确,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为：连半径,证垂直。
(2)如果直线与圆的交点不明确,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为：作垂直,证半径。例1、已知：直线AB经过⊙O上的点C，
并且OA=OB,CA=CB.
求证：直线AB是⊙O的切线。
例2、已知O为∠BAC平分线上一点，OD⊥AB于D，
以O为圆心，OD为半径作圆O，求证：⊙O与AC相切 如图、已知OA＝OB＝5厘米，AB＝8厘米，⊙O的直径为6厘米.
求证：AB与⊙O相切分析：因为已知条件没给出AB和⊙O有公共点，所以可过圆心O作OC⊥AB，垂足为C.只需证明OC等于⊙O的半径3厘米即可.练一练体会.分享.反思说能出你这节课的收获和体验让大家与你分享吗？课堂小结1. 判定切线的方法有哪些？直线l 与圆有唯一公共点与圆心的距离等于圆的半径经过半径外端且垂直这条半径l是圆的切线2. 常用的添辅助线方法 ⑴直线与圆的公共点已知时，作出过公共点的半径，再证半径垂直于该直线。（连半径，证垂直）
⑵直线与圆的公共点不确定时，过圆心作直线的垂线段，再证明这条垂线段等于圆的半径。
（作垂直，证半径）l是圆的切线l是圆的切线 ⑴、经过半径外端的直线是圆的切线。
⑵、垂直于半径的直线是圆的切线。
⑶、过直径的外端并且垂直于这条直径的
直线是圆的切线。
⑷、和圆只有一个公共点的直线是圆的切
线。
⑸、以等腰三角形的顶点为圆心，底边上
的高为半径的圆与底边相切。
是非题：判断下列命题是否正确。（×）（×）（√）（√）（√）解答题1、如图1，△AOB中，OA＝OB＝10，∠AOB＝120°，
以O为圆心，5为半径的⊙O与OA、OB相交。
求证：AB是⊙O的切线。 OBA2、如图2,△ABC中，AB=AC，以AB为直径的⊙O交边BC于P， PE⊥AC于E。
求证:PE是⊙O的切线。OABCEP图1图2小结已知△ABC内接于⊙O,直线EF过点A（1）如图1，AB为直径，要使得EF是⊙O的切线，还需添加的条件是 或 。
（2）如图2， AB为非直径弦，且∠CAE=∠B,求证：EF为⊙O的切线。思考题图1图2EF⊥AB∠CAE=∠B结 束 寄 语不经历风雨，怎能见彩虹！再 见