西南师大版五年级数学上册三除数是整数的除法教学设计
文档属性
| 名称 | 西南师大版五年级数学上册三除数是整数的除法教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 133.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-08 00:00:00 | ||
图片预览


文档简介
除数是整数的小数除法
教学内容
小学五年级上册第45页(西师版)
教学目标
1、使学生学会除数是整数的小数除法的计算方法。
2、理解除数是整数的小数除法的计算方法跟整数除法之间的关系,促进学习迁移。
3、体验所学知识与现实生活的联系,从中获得价值体验。
教学重难点
重点:理解掌握除数是整数的小数除法的计算方法。
难点:理解商的小数点定位问题。
教学方法
小组合作探究
教学过程
1、复习导入
1.填空:
0.25里面含有25个( )。
0.63里面含有( )个百分之一。
0.7里面含有7个( )。
1.3里面含有( )个十分之一。
2.计算:
4800÷400=( )
480÷40=( )
48÷4=( )
4.8÷4=( )
2、探究新知
(一)例题1:
小华、小红、小聪、小进4个小朋友一起到人森林公园去玩,购买门票一共花了33.6元,问平均每人购买门票花了多少钱?
1、怎样列式
总价÷数量=单价
33.6 ÷ 4 =( )
2、学生讨论后教师展示(见课件)
3、观察下面的两个竖式计算,你发现它们有哪些地方相同?有哪些地方不同?)(见课件)
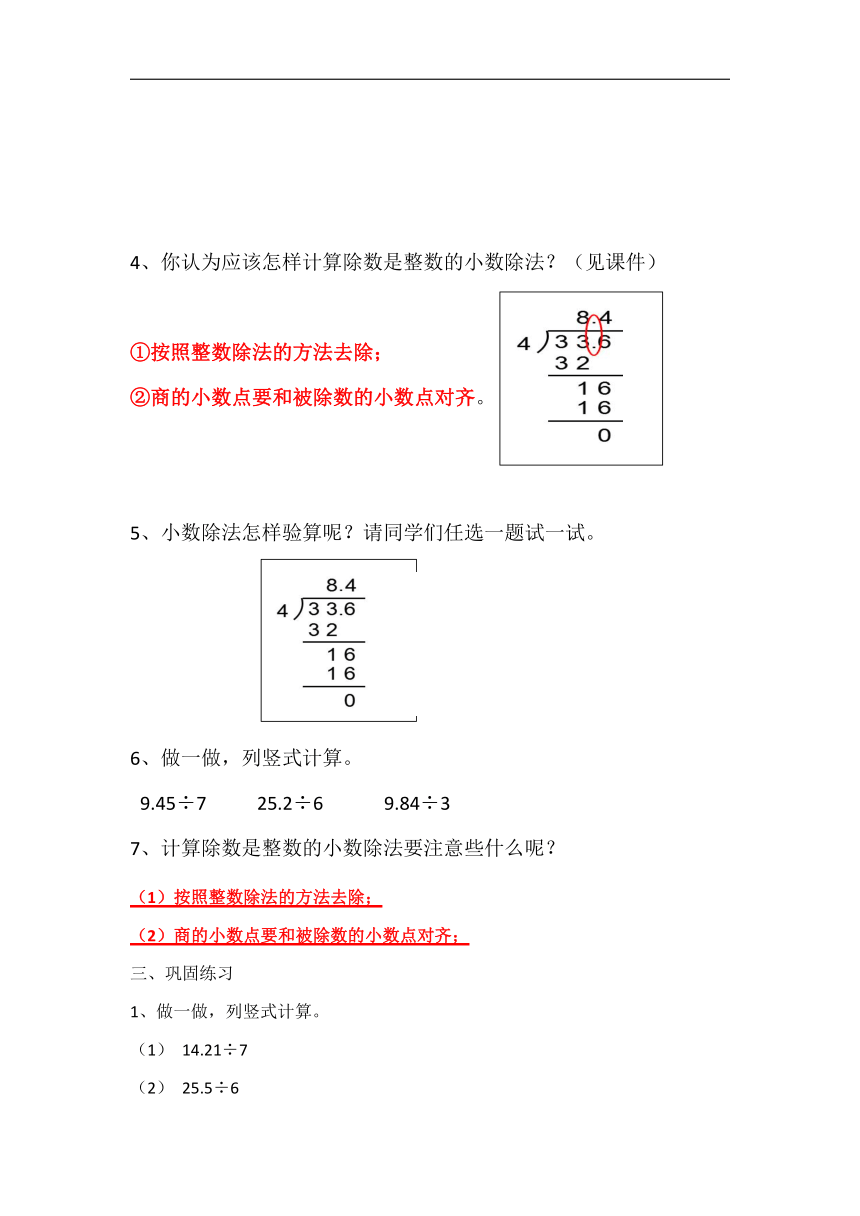
4、你认为应该怎样计算除数是整数的小数除法?(见课件)
①按照整数除法的方法去除;
②商的小数点要和被除数的小数点对齐。
5、小数除法怎样验算呢?请同学们任选一题试一试。
6、做一做,列竖式计算。
9.45÷7 25.2÷6 9.84÷3
7、计算除数是整数的小数除法要注意些什么呢?
(1)按照整数除法的方法去除;
(2)商的小数点要和被除数的小数点对齐;
三、巩固练习
1、做一做,列竖式计算。
(1) 14.21÷7
(2) 25.5÷6
2、算一算,比一比。
45÷3 52÷13 121÷11 100÷25
4.5÷3 0.52÷13 1.21÷11 1÷25
3、下面的计算对吗?如果不对,错在哪里?
四、课堂总结。
1、小数除以整数,按照整数除法的法则去除,商的小数点要和被除数的小数点对齐。
2、除到被除数的哪一位,商就写在那一位上。
5、作业练习
课本P.48练习十一第1、6题。
《除数是整数的小数除法》教学反思
宣汉县东乡镇西北中心校 朱 峰
《除数是整数的小数除法》是西师版五年级上册第3单元的内容,本节课以四位同学到公园买票的生活事例引入新课,这样充分调动了学生的学习积极性。因此这节课我着重让学生从已有生活经验和借助已有生活知识,通过自主探索与交流,发现除数是整数的小数除法的计算方法,并在实际情境中体会感受小数除法的意义。在教学中注意做到以下几点:
一、课前复习相关知识
第一复小数的计数单位,第二复习整数除法,商的不变规律,引出除数是整数的小数除法。因此,从课堂上学生学习过程来看,学生能把整数除法的计算方法迁移到被除数是小数的除法上来,这充分说明新课前的复习是很有必要的。
二、创设情境与生活实际的紧密联系
本课的基本教学策略是引导学生把除数是整数的除法
转化成前面学过的整数除法。为了激发学生的学习兴趣,提高学习热情,现实生活既是计算教学的源头,更是计算教学的归宿。创设学生所熟悉的公园买票的场景,由此引出所探究的内容,突出生活实际的主题,自然的引入小数除法,让学生在具体的情境中感受体会小数除法的意义,激发学生探究小数除法的兴趣。
三、 组织学生自主探究、合作交流,同时体现算法多样化
新课标要求学生应当经历数学的学习过程,在自主探究和合作交流的过程当中学习知识,掌握数学的学习方法。因此学生明确小数除法的意义后,引导学生探究计算方法,先让学生试算,再小组交流,然后集体汇报,从而概括出合理简便的计算法,大胆的放手让学生独立尝试想办法计算商。力求让学生独立探究发现。课堂中我给予学生充足的时间探究“除数是整数的小数除法”的算理,而且充分交流,引导相互的理解,学生解决新问题的办法很多,对算理的理解也较为透彻,从而,使学生自己学会解决问题的方法,增强学习数学的综合能力。通过小组讨论,然后汇报,最后归纳出商的小数点和被除数的小数点应对齐。这样将课堂充分的交给学生,而教师作为一个引导者和组织者,让学生自己探索,组织学生相互质疑,合作讨论,使学生体验到成功的喜悦。
四、 归纳小结,巩固提高。
本节课归纳小结主要从两方面:第一归纳计算方法,第二让学生说一说在计算中要注意什么。设计了3道课堂训练题,3组巩固练习题和2道课后作业题。主要内容联系实际,这样既紧扣精打细算的主题,又巩固刚学的知识。在本节课的教学过程当中,也有不足之处。
2、要关注学生的学习。 不仅要关注学生是否在听课,更要关注学生的思维过程。特别是在学生练习时,要注意观察学生的计算过程。
3、计算方法的揭示太匆忙,学生没有较好掌握。原因是我没有在算理和算法之间很好地“搭建桥梁”,计算方法基本属于结论教学,没有有效的引导理解、概括的过程。导致在练习中很多学生都用算理来计算题目,而没有用方法来计算。
经过上课,我反复思考,我认为对计算教学应算理与算法齐头并进的予以重视,同时在算理和算法之间搭建有机桥梁,这样,当学生真正理解了算理时,学会算法便是水到渠成的事。
教学内容
小学五年级上册第45页(西师版)
教学目标
1、使学生学会除数是整数的小数除法的计算方法。
2、理解除数是整数的小数除法的计算方法跟整数除法之间的关系,促进学习迁移。
3、体验所学知识与现实生活的联系,从中获得价值体验。
教学重难点
重点:理解掌握除数是整数的小数除法的计算方法。
难点:理解商的小数点定位问题。
教学方法
小组合作探究
教学过程
1、复习导入
1.填空:
0.25里面含有25个( )。
0.63里面含有( )个百分之一。
0.7里面含有7个( )。
1.3里面含有( )个十分之一。
2.计算:
4800÷400=( )
480÷40=( )
48÷4=( )
4.8÷4=( )
2、探究新知
(一)例题1:
小华、小红、小聪、小进4个小朋友一起到人森林公园去玩,购买门票一共花了33.6元,问平均每人购买门票花了多少钱?
1、怎样列式
总价÷数量=单价
33.6 ÷ 4 =( )
2、学生讨论后教师展示(见课件)
3、观察下面的两个竖式计算,你发现它们有哪些地方相同?有哪些地方不同?)(见课件)
4、你认为应该怎样计算除数是整数的小数除法?(见课件)
①按照整数除法的方法去除;
②商的小数点要和被除数的小数点对齐。
5、小数除法怎样验算呢?请同学们任选一题试一试。
6、做一做,列竖式计算。
9.45÷7 25.2÷6 9.84÷3
7、计算除数是整数的小数除法要注意些什么呢?
(1)按照整数除法的方法去除;
(2)商的小数点要和被除数的小数点对齐;
三、巩固练习
1、做一做,列竖式计算。
(1) 14.21÷7
(2) 25.5÷6
2、算一算,比一比。
45÷3 52÷13 121÷11 100÷25
4.5÷3 0.52÷13 1.21÷11 1÷25
3、下面的计算对吗?如果不对,错在哪里?
四、课堂总结。
1、小数除以整数,按照整数除法的法则去除,商的小数点要和被除数的小数点对齐。
2、除到被除数的哪一位,商就写在那一位上。
5、作业练习
课本P.48练习十一第1、6题。
《除数是整数的小数除法》教学反思
宣汉县东乡镇西北中心校 朱 峰
《除数是整数的小数除法》是西师版五年级上册第3单元的内容,本节课以四位同学到公园买票的生活事例引入新课,这样充分调动了学生的学习积极性。因此这节课我着重让学生从已有生活经验和借助已有生活知识,通过自主探索与交流,发现除数是整数的小数除法的计算方法,并在实际情境中体会感受小数除法的意义。在教学中注意做到以下几点:
一、课前复习相关知识
第一复小数的计数单位,第二复习整数除法,商的不变规律,引出除数是整数的小数除法。因此,从课堂上学生学习过程来看,学生能把整数除法的计算方法迁移到被除数是小数的除法上来,这充分说明新课前的复习是很有必要的。
二、创设情境与生活实际的紧密联系
本课的基本教学策略是引导学生把除数是整数的除法
转化成前面学过的整数除法。为了激发学生的学习兴趣,提高学习热情,现实生活既是计算教学的源头,更是计算教学的归宿。创设学生所熟悉的公园买票的场景,由此引出所探究的内容,突出生活实际的主题,自然的引入小数除法,让学生在具体的情境中感受体会小数除法的意义,激发学生探究小数除法的兴趣。
三、 组织学生自主探究、合作交流,同时体现算法多样化
新课标要求学生应当经历数学的学习过程,在自主探究和合作交流的过程当中学习知识,掌握数学的学习方法。因此学生明确小数除法的意义后,引导学生探究计算方法,先让学生试算,再小组交流,然后集体汇报,从而概括出合理简便的计算法,大胆的放手让学生独立尝试想办法计算商。力求让学生独立探究发现。课堂中我给予学生充足的时间探究“除数是整数的小数除法”的算理,而且充分交流,引导相互的理解,学生解决新问题的办法很多,对算理的理解也较为透彻,从而,使学生自己学会解决问题的方法,增强学习数学的综合能力。通过小组讨论,然后汇报,最后归纳出商的小数点和被除数的小数点应对齐。这样将课堂充分的交给学生,而教师作为一个引导者和组织者,让学生自己探索,组织学生相互质疑,合作讨论,使学生体验到成功的喜悦。
四、 归纳小结,巩固提高。
本节课归纳小结主要从两方面:第一归纳计算方法,第二让学生说一说在计算中要注意什么。设计了3道课堂训练题,3组巩固练习题和2道课后作业题。主要内容联系实际,这样既紧扣精打细算的主题,又巩固刚学的知识。在本节课的教学过程当中,也有不足之处。
2、要关注学生的学习。 不仅要关注学生是否在听课,更要关注学生的思维过程。特别是在学生练习时,要注意观察学生的计算过程。
3、计算方法的揭示太匆忙,学生没有较好掌握。原因是我没有在算理和算法之间很好地“搭建桥梁”,计算方法基本属于结论教学,没有有效的引导理解、概括的过程。导致在练习中很多学生都用算理来计算题目,而没有用方法来计算。
经过上课,我反复思考,我认为对计算教学应算理与算法齐头并进的予以重视,同时在算理和算法之间搭建有机桥梁,这样,当学生真正理解了算理时,学会算法便是水到渠成的事。
