8.3怎样判断三角形全等

课件30张PPT。§8.2 怎样判定三角形全等第八章 平面图形的全等与相似青岛版义务教育教材八年级下册
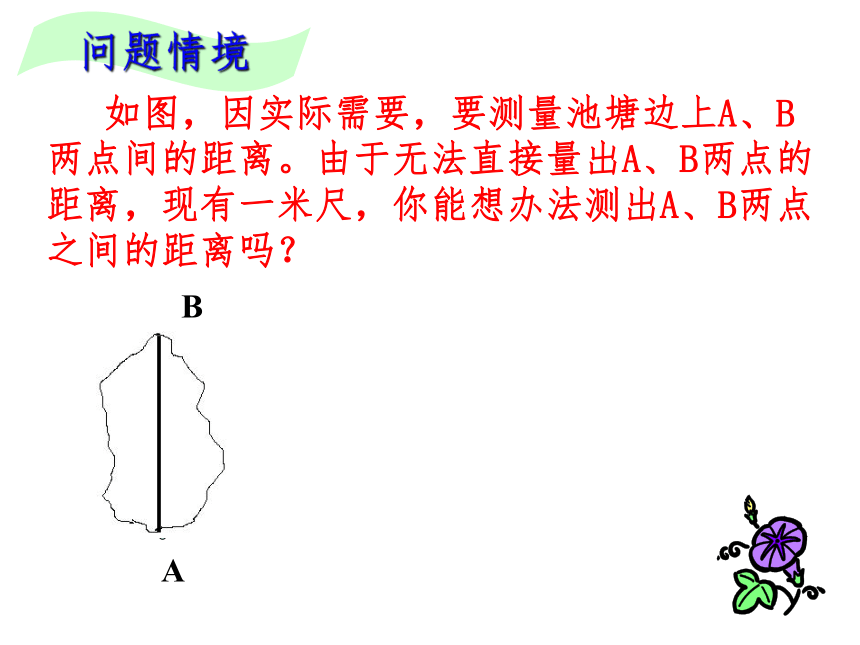
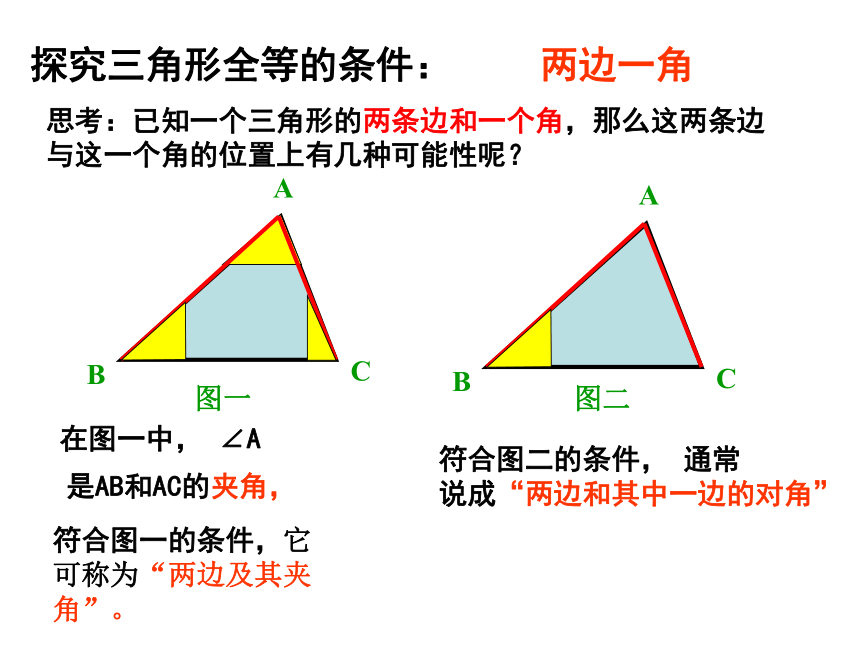
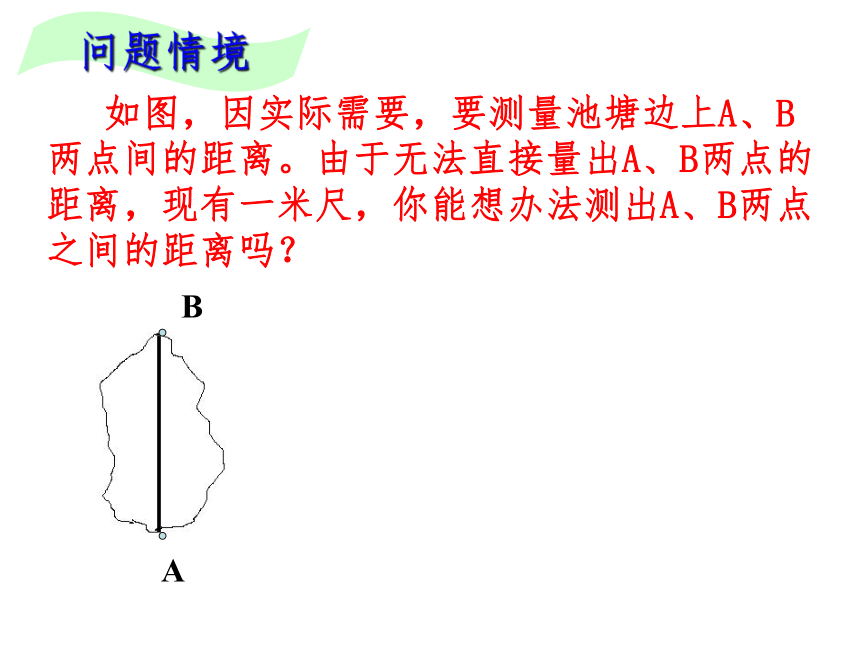
问题情境 如图，因实际需要，要测量池塘边上A、B两点间的距离。由于无法直接量出A、B两点的距离，现有一米尺，你能想办法测出A、B两点之间的距离吗？ “角边角”以及“角角边”都是通过两个三角形的三对对应元素相等来判断两个三角形全等的，那么两边一角、三条边和三个角分别对应相等的两个三角形是否也全等呢？思考 这节课我们将重点探究“两边一角” 分别对应相等的两个三角形是否全等？探究三角形全等的条件：两边一角思考：已知一个三角形的两条边和一个角，那么这两条边
与这一个角的位置上有几种可能性呢？图一图二在图一中， ∠A是AB和AC的夹角，符合图一的条件，它可称为“两边及其夹角”。符合图二的条件， 通常
说成“两边和其中一边的对角”探究一：两边及其夹角分别对应相等的两个三角形是否全等？1、已知∠A（图一），请你在∠A上画出△ABC，使得AB=6厘米，AC=4厘米；
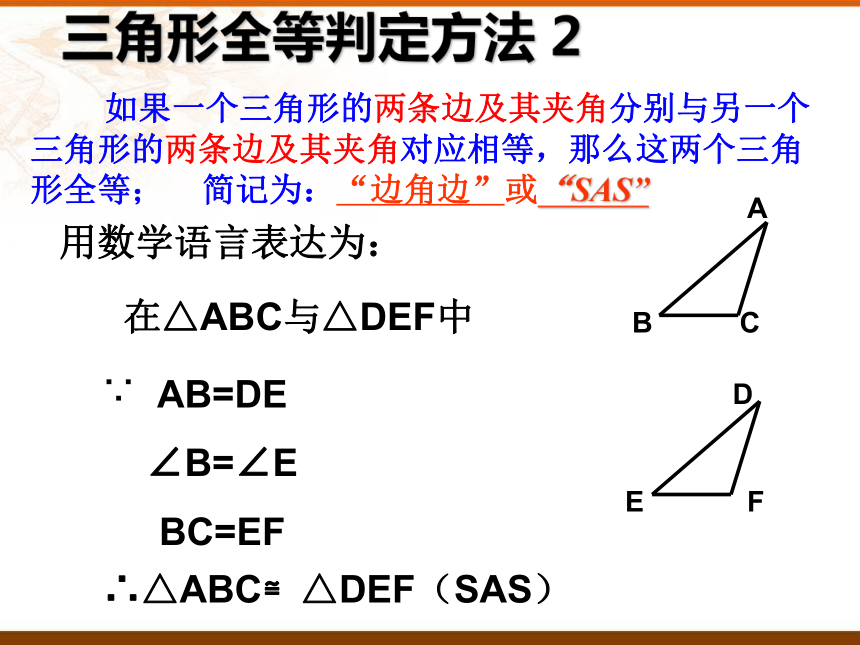
2、剪下你画出的三角形，与其他同学剪得的三角形进行比较，这些三角形能重合吗？3、已知∠E （图二）， 请你在∠E上画出△DEF，使得ED=6厘米，EF=4厘米；剪下你画出的三角形，与其他同学剪得的三角形进行比较，这些三角形能重合吗？4、已知∠M （图三） ，请你在∠M上画出△MNP，使得MN=3厘米，MP=5厘米；剪下你画出的三角形，与其他同学剪得的三角形进行比较，这些三角形能重合吗？通过上面的实验探究，你能得出什么样的结论？探究一：两边及其夹角分别对应相等的两个三角形是否全等？ 如果一个三角形的两条边及其夹角分别与另一个三角形的两条边及其夹角对应相等，那么这两个三角形全等； 简记为：“边角边”或“SAS” 三角形全等判定方法 2用数学语言表达为：在△ABC与△DEF中AB=DE
∠B=∠E
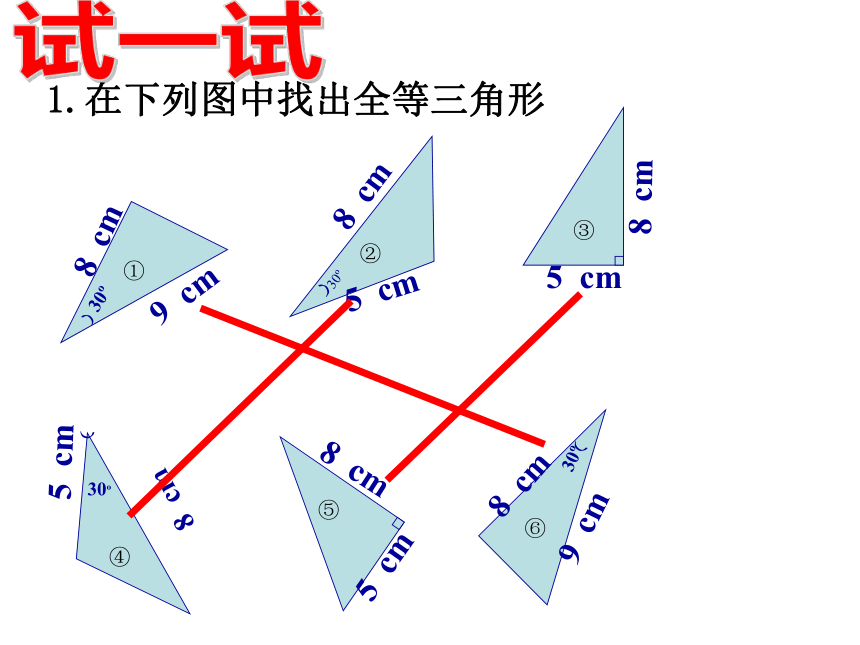
BC=EF∴△ABC≌△DEF（SAS）∵1.在下列图中找出全等三角形试一试C2、在下列推理过程中填写需要补充
的条件，使结论成立：
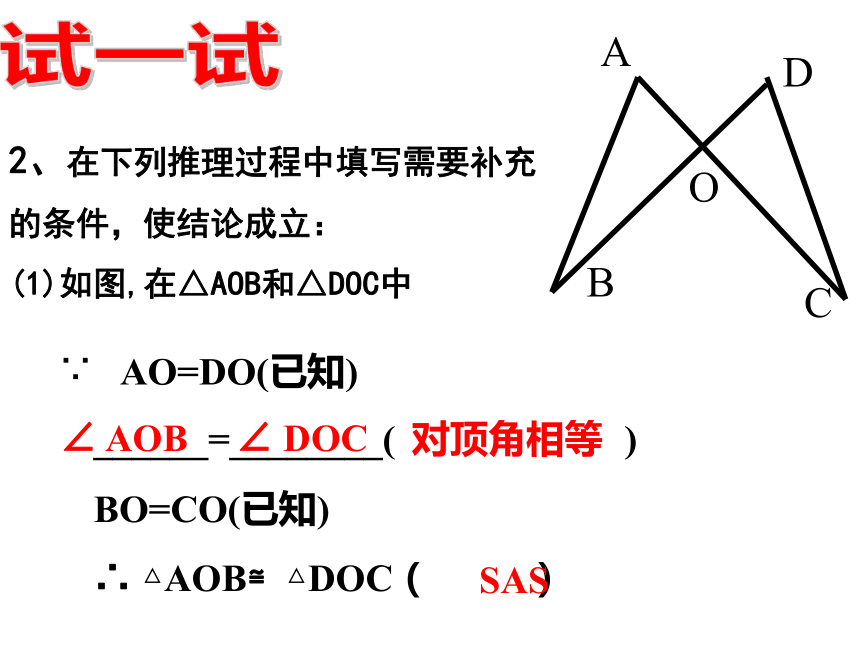
(1)如图,在△AOB和△DOC中 AO=DO(已知)
______=________( )
BO=CO(已知)
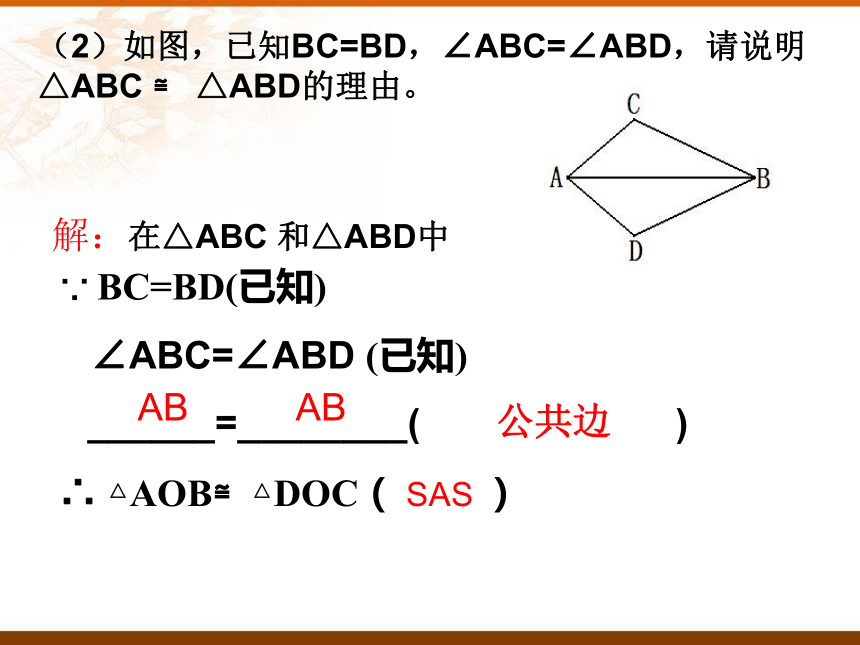
∴ △AOB≌△DOC（ ）∠ AOB∠ DOC对顶角相等SAS试一试∵（2）如图，已知BC=BD，∠ABC=∠ABD，请说明△ABC ≌ △ABD的理由。 BC=BD(已知)
∠ABC=∠ABD (已知)
______=________( )
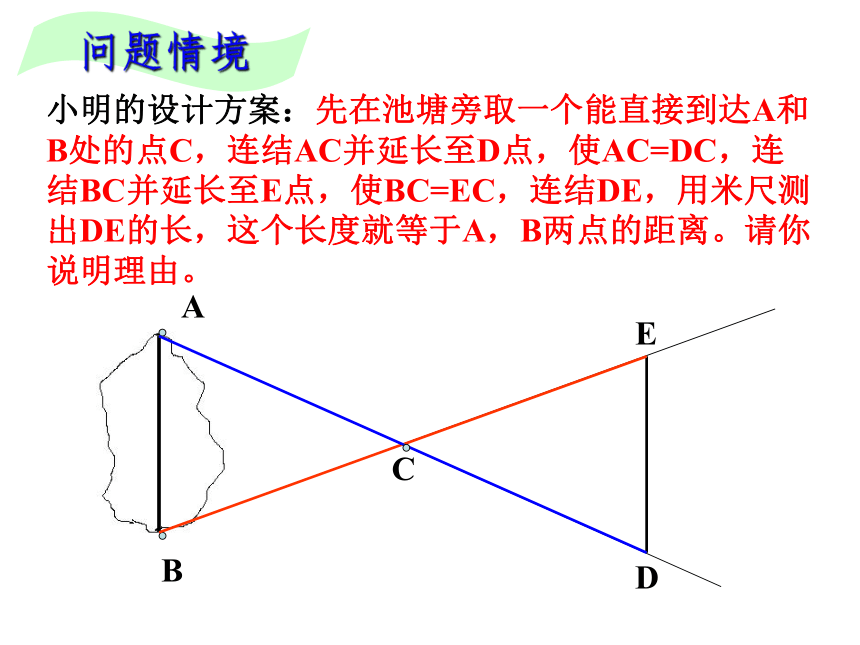
∴ △AOB≌△DOC（ SAS ）∵AB公共边AB解：在△ABC 和△ABD中 如图，因实际需要，要测量池塘边上A、B两点间的距离。由于无法直接量出A、B两点的距离，现有一米尺，你能想办法测出A、B两点之间的距离吗？问题情境小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结DE，用米尺测出DE的长，这个长度就等于A，B两点的距离。请你说明理由。ED问题情境
如图，已知OA=OB,再添加什么条件就能得到：
△AOC≌ △BOD(只允许添加一个条件)开放题:AS∠A = ∠BAASSASASA∠C = ∠DOC = OD两边及其中一边的对角对应相等的两个三角形全等吗? 已知：∠A=45 °（图4），请你在∠A上画出△ABC，使得AC=6cm, CB=5cm, ；剪下你画出的三角形，与其他同学剪得的三角形进行比较，这些三角形能重合吗？△ABC的形状与大小是唯一确定的吗?探究二：两边及其一边的对角两边及其中一边的对角对应相等的两个三角形全等吗?已知：AC=6cm,BC=5cm, ∠A=45 °.探究二：两边及其一边的对角探索边边角SSA不存在显然： △ABC与△AB’C不全等ABDABCSSA不能判定全等拓展训练 1、如图，已知AC=AD，∠BAC=∠BAD，请说明∠C=∠D的理由。在△ABC和△DEF中解：∵ AC=AD
∠BAC=∠BAD
AB=AB∴ △ABC≌△ABD∴ ∠C=∠D拓展训练 变式一：
如图，已知AC=DE，∠A=∠DEF，AE=FB，请说明BC=FD的理由。你有什么收获？你认为本节课
需要注意的
问题是什么？分享收获的快乐你是好样的，我相信当堂达标1、填空（每空15分，共60分）
如果一个三角形的 分别与另一个三角形的两条边及其夹
角 ，那么这两个三角形全等；
简记为：“ ”或“ ”； 2、（30分）如图，如图，用工具测量零件的内径BD，已知OA=OB，OC=OD，经测量AC=5cm，那么零件的内径BD= ；
3、（本题30分）如图已知，∠ABC =∠DCB，再添加条件 时，
△ABC≌△DCB；（只需添加一种即可）两边及其夹角 对应相等 边角边 SAS 5cm（1）AB=DC
（2） ∠A=∠D
（3） ∠ACB=∠DBC你是好样的，我相信当堂达标4、（2011·泉州）（30分）如图，已知点E、C在线段BF上，BE=CF，AC=DF，∠ACB=∠F.
求证：△ABC≌△DEF.∵ BE=CF
∴BC=EF在△ABC和△DEF中证明：∵ AC=DF
∠ACB=∠F
BC=EF∴ △ABC≌△DEF作业：自主作业：
已知：如图，AD=CB，AD∥BC.
试说明AB=CD.(你一定能想出办法，加油！） 谢谢1、已知：如图AB=AC,AD=AE,∠BAC=∠DAE
求证： ∠B=∠C练一练巩固练习2.如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C
求证：∠A=∠D
例3.已知：如图，AD=CB，AD∥BC.
求证：AB=CD.(你一定能想出办法.）分析：连结AC.
证△ABC≌ △CDA.分析：连结BD.
证△ABD≌△CDB.
三步走：①准备条件②摆齐条件③得结论注重书写格式两角及其夹边分别对应相等的两个三角形全等
（简记为：“角边角”或“ASA”）。在△ABC和△ DEF中∴ △ABC ≌△ DEF（ASA）∠ B= ∠E
BC=EF
∠ C= ∠ F用符号语言表达为： 三角形全等判定方法1∵两角及其一角的对边分别对应相等的两个三角形全等（简记为：“角角边”或“AAS”）在△ABC和△ DEF中∴ △ABC ≌△ DEF（AAS）∠ B= ∠E
∠ C= ∠ F
AC=DF用符号语言表达为： 三角形全等判定方法1—推论∵