7.2复数的四则运算 教案
文档属性
| 名称 | 7.2复数的四则运算 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 139.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 14:38:48 | ||
图片预览




文档简介
复数的四则运算
【教学目标】
1.知识与技能
理解并掌握复数的代数形式的乘法与除法运算法则,了解共轭复数的概念。
2.过程与方法
理解并掌握复数的除法运算实质是分母实数化问题,通过运算过程体会这一变形本质意图。
3.情感、态度与价值观
利用多项式除法和复数除法类比,知道事物之间是普遍联系的。通过复数除法运算,培养学生探索问题、分析问题、解决问题的能力。
【教学重难点】
重点:复数代数形式的乘除法运算。
难点:复数除法法则的运用。
【教学建议】
建议本节教学采用自学指导法,在学生自主学习的基础上可利用一下教学方法及手段完成本节教学:(1)类比分析法,通过对比多项式的乘法法则推出复数乘法法则。(2)归纳推理法,运用已有的多项式乘法法则和分母有理化及复数加减法的知识,通过归纳类比,推导复数除法法则。(3)合理、恰当地运用多媒体教学手段,将静态事物动态化,将抽象事物直观化,以突破教学难点。
【教学过程】
创设问题情境,引出问题,引导学生思考两个复数如何进行代数形式的乘法与除法运算。?让学生自主完成填一填,使学生进一步熟悉复数代数形式的乘法、除法运算的法则,及其满足的运算律。引导学生分析例题1的运算方法并求解,教师只需指导完善,解答疑惑并要求学生独立完成变式训练。由学生分组探究例题2解法,引导学生去发现in运算的周期性,及其应用方法。完成互动探究。
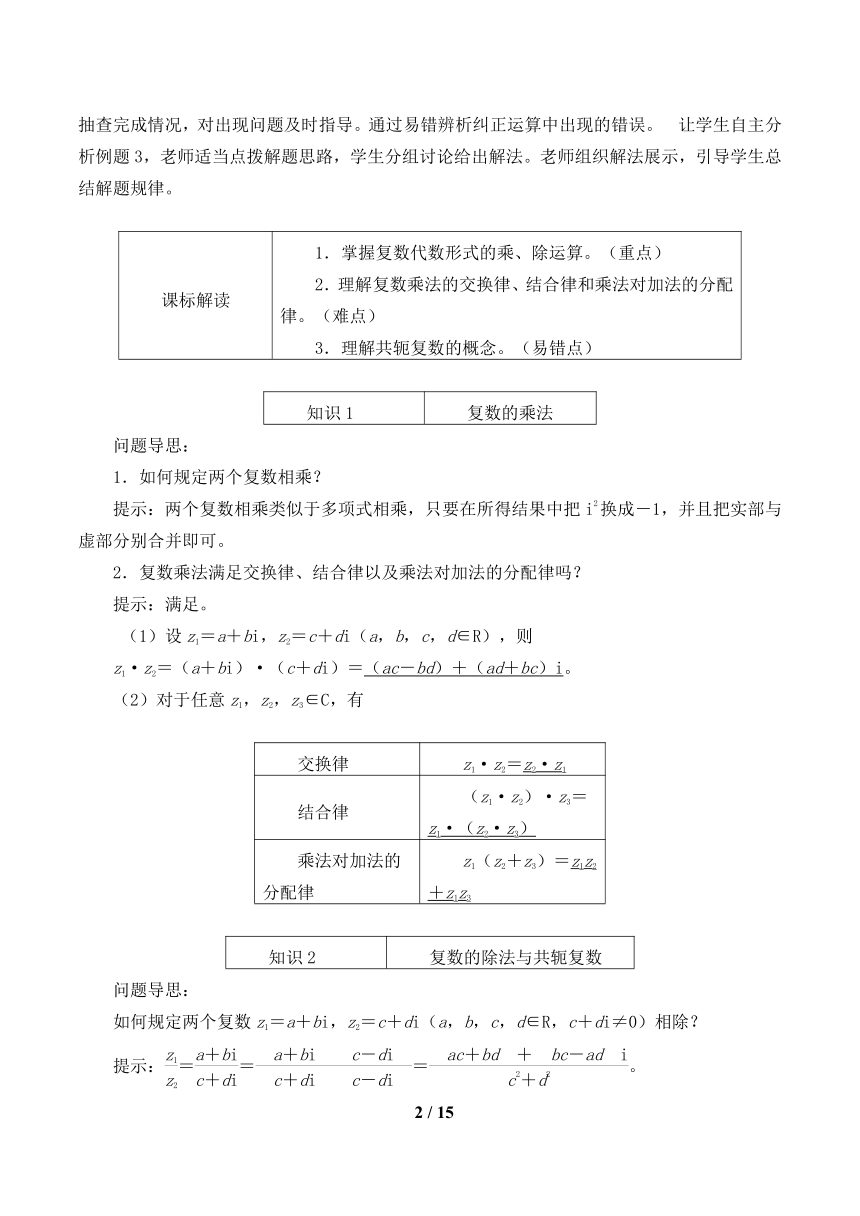
完成当堂双基达标,巩固所学知识及应用方法。并进行反馈矫正。归纳整理,进行课堂小结,整体认识本节所学知识,强调重点内容和规律方法。学生自主完成例题3变式训练,老师抽查完成情况,对出现问题及时指导。通过易错辨析纠正运算中出现的错误。?让学生自主分析例题3,老师适当点拨解题思路,学生分组讨论给出解法。老师组织解法展示,引导学生总结解题规律。
课标解读 1.掌握复数代数形式的乘、除运算。(重点)2.理解复数乘法的交换律、结合律和乘法对加法的分配律。(难点)3.理解共轭复数的概念。(易错点)
知识1 复数的乘法
问题导思:
1.如何规定两个复数相乘?
提示:两个复数相乘类似于多项式相乘,只要在所得结果中把i2换成-1,并且把实部与虚部分别合并即可。
2.复数乘法满足交换律、结合律以及乘法对加法的分配律吗?
提示:满足。
(1)设z1=a+bi,z2=c+di(a,b,c,d∈R),则
z1·z2=(a+bi)·(c+di)=(ac-bd)+(ad+bc)i。
(2)对于任意z1,z2,z3∈C,有
交换律 z1·z2=z2·z1
结合律 (z1·z2)·z3=z1·(z2·z3)
乘法对加法的分配律 z1(z2+z3)=z1z2+z1z3
知识2 复数的除法与共轭复数
问题导思:
如何规定两个复数z1=a+bi,z2=c+di(a,b,c,d∈R,c+di≠0)相除?
提示:===。
(1)z1=a+bi,z2=c+di(a,b,c,d为实数,c+di≠0),z1,z2进行除法运算时,通常先把(a+bi)÷(c+di)写成的形式再把分子与分母都乘以c-di化简后可得结果:+i。
(2)共轭复数
如果两个复数满足实部相等,虚部互为相反数时,称这两个复数为共轭复数,z的共轭复数用表示。即z=a+bi,则=a-bi。虚部不等于0的两个共轭复数也叫共轭虚数。
知识1 复数代数形式的乘除法运算
例1:(1)(2013·课标全国卷Ⅱ)设复数z满足(1-i)·z=2i,则z=( )
A.-1+i B.-1-i C.1+i D.1-i
(2)(2013·大纲全国卷)(1+i)3=( )
A.-8 B.8 C.-8i D.8i
(3)计算()6+=________。
思路探究:(1)先设出复数z=a+bi,然后运用复数相等的充要条件求出a,b的值。
(2)直接利用复数的乘法运算法则计算。
(3)先计算再乘方,且将的分母实数化后再合并。
自主解答:(1)设z=a+bi,则(1-i)(a+bi)=2i,即(a+b)+(b-a)i=2i。
根据复数相等的充要条件得解得
∴z=-1+i。故选A.
(2)原式=(1+i)(1+i)2=(1+i)(-2+2i)=-2+6i2=-8.
(3)法一:原式=6+
=i6+=-1+i。
法二 原式=6+
=i6+
=-1+i。
答案:(1)A (2)A (3)-1+i
规律方法
1.复数的乘法类比多项式相乘进行运算,复数除法要先写成分式形式后,再将分母实数化,注意最后结果要写成a+bi(a,b∈R)的形式。
2.记住以下结论可以提高运算速度
(1)(1+i)2=2i,(1-i)2=-2i;
(2)=-i,=i;
(3)=-i。
变式训练
计算:
(1)(1-i)2;
(2)(-+i)(+i)(1+i);
(3)。
解:(1)(1-i)2=1-2i+i2=-2i。
(2)(-+i)(+i)(1+i)
=(--i+i+i2)(1+i)
=(-+i-)(1+i)
=(-+i)(1+i)
=--i+i-
=-+i。
(3)===+i。
知识2 虚数单位i的幂的周期性及其应用
例2: (1)计算:+()2 013;
(2)若复数z=,求1+z+z2+…+z2 013的值。
思路探究:将式子进行适当的化简、变形,使之出现in的形式,然后再根据in的值的特点计算求解。
自主解答:(1)原式=+[()2]1 006·()
=i+()1 006·=i+i1 006·
=-+i
(2)1+z+z2+…+z2 013=,
而z====i,
所以1+z+z2+…+z2 013===1+i。
规律方法
1.要熟记in的取值的周期性,要注意根据式子的特点创造条件使之与in联系起来以便计算求值。
2.如果涉及数列求和问题,应先利用数列方法求和后再求解。
互动探究
在本例(2)中若z=i,求1+z+z2+…+z2 013的值。
解:由题意知
1+z+z2+…+z2 013=1+i+i2+…+i2 013
====1+i。
∴原式=1+i。
知识3 共轭复数的应用
例3:设z1,z2∈C,A=z1·+z2·,B=z1·+z2·,问A与B是否可以比较大小?为什么?
思路探究:设出z1,z2的代数形式→化简A,B→判断A,B是否同为实数→结论
自主解答:设z1=a+bi,
z2=c+di(a,b,c,d∈R),
则=a-bi,=c-di,
∴A=z1·+z2·
=(a+bi)(c-di)+(c+di)(a-bi)
=ac-adi+bci-bdi2+ac-bci+adi-bdi2
=2ac+2bd∈R,
B=z1·+z2·
=|z1|2+|z2|2
=a2+b2+c2+d2∈R,
∴A与B可以比较大小。
规律方法
1.z·=|z|2=||2是共轭复数的常用性质。
2.实数的共轭复数是它本身,即z∈R z=,利用此性质可以证明一个复数是实数。
3.若z≠0且z+=0,则z为纯虚数,利用此性质可证明一个复数是纯虚数。
变式训练
已知z∈C,为z的共轭复数,若z·-3i=1+3i,求z。
解:设z=a+bi(a,b∈R),则=a-bi(a,b∈R),
由题意得(a+bi)(a-bi)-3i(a-bi)=1+3i,
即a2+b2-3b-3ai=1+3i,
则有,
解得或,
所以z=-1或z=-1+3i。
典例:设复数z满足=i,则z=( )
A.-2+I B.-2-i
C.2-i D.2+i
错解:设复数z=a+bi(a,b∈R)满足=i,
所以1+2i=ai+B.
解得
所以z=2+i,故选D项。
答案:D
错因分析:将i2=-1当成i2=1来运算漏掉负号。
防范措施:在进行乘除法运算时,灵活运用i的性质,并注意一些重要结论的灵活应用。
正解:设复数z=a+bi(a,b∈R)满足=i,
所以1+2i=ai-B.
解得
所以z=2-i,故选C项。
答案:C
课堂小结
1.复数代数形式的乘除运算
(1)复数代数形式的乘法类似于多项式乘以多项式,复数的乘法满足交换律、结合律以及乘法对加法的分配律。
(2)在进行复数代数形式的除法运算时,通常先将除法写成分式的形式,再把分子、分母都乘以分母的共轭复数,化简后可得,类似于以前学习的分母有理化。
2.共轭复数的性质可以用来解决一些复数问题。
3.复数问题实数化思想。
复数问题实数化是解决复数问题的基本思想方法,其桥梁是设复数z=a+bi(a,b∈R),利用复数相等的充要条件转化。
当堂双基达标
1.(2012·北京高考)在复平面内,复数对应的点的坐标为( )
A.(1,3) B.(3,1)
C.(-1,3) D.(3,-1)
解析:===1+3i,
∴其对应点的坐标为(1,3),选A.
答案:A
2.(2013·安徽高考)设i是虚数单位,若复数a-(a∈R)是纯虚数,则a的值为( )
A.-3 B.-1
C.1 D.3
解析:因为a-=a-=a-=(a-3)-i,由纯虚数的定义,知a-3=0,所以a=3.
答案:D
3.若x-2+yi和3x-i互为共轭复数,则实数x=________,y=________。
解析:由题意得:
∴
答案:-1、1
4.计算:
(1)(1-i)(-+i)(1+i);
(2);
(3)(2-i)2.
解:(1)法一:(1-i)(-+i)(1+i)
=(-+i+i-i2)(1+i)
=(+i)(1+i)
=+i+i+i2
=-1+i。
法二:原式=(1-i)(1+i)(-+i)
=(1-i2)(-+i)
=2(-+i)
=-1+i。
(2)=
=
=
==i。
(3)(2-i)2=(2-i)(2-i)
=4-4i+i2
=3-4i。
课后知能训练
一、选择题
1.复数(2+i)2等于( )
A.3+4i B.5+4i
C.3+2i D.5+2i
解析:(2+i)2=4+4i+i2=4+4i-1=3+4i。故选A.
答案:A
2.i是虚数单位,复数=( )
A.1-i B.-1+i
C.1+i D.-1-i
解析:===1+i。
答案:C
3.若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
A.-4 B.-
C.4 D.
解析:∵(3-4i)z=|4+3i|,∴z====+i,∴z的虚部为。
答案:D
4.若z+=6,z·=10,则z=( )
A.1±3i B.3±i
C.3+i D.3-i
解析:设z=a+bi(a,b∈R),则=a-bi,
∴,解得a=3,b=±1,则z=3±i。
答案:B
5.(2013·湖北高考)在复平面内,复数z=(i为虚数单位)的共轭复数对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:z===1+i,所以=1-i,故复数z的共轭复数对应的点位于第四象限。
答案:D
二、填空题
6.(2013·江苏高考)设z=(2-i)2(i为虚数单位),则复数z的模为________。
解析:z=(2-i)2=3-4i,所以|z|=|3-4i|==5.
答案:5
7.若=a+bi(a,b为实数,i为虚数单位),则a+b=________。
解析:=
=[(3-b)+(3+b)i]=+i。
∴解得∴a+b=3.
答案:3
8.当z=-时,z2 012+z2 014=________。
解析:z=-,∴z2==-i,
∴z2 012=(-i)2 012=1,
z2 014=(-i)2 014=-1,
∴z2 012+z2 014=1-1=0.
答案:0
三、解答题
9.计算下列各题:
(1)+-;
(2)(+i)5+()4+()7;
(3)(--i)12+()8.
解:(1)原式=[(1+i)2]3+[(1-i)2]3·-
=(2i)3·i+(-2i)3·(-i)-
=8+8-16-16i=-16i。
(2)(+i)5+()4+()7
=-i·()5·[(1+i)2]2·(1+i)+[]2+i7
=16(-1+i)--i
=-(16+)+(16-1)i。
(3)(--i)12+()8
=(-i)12·(--i)12+()8
=(-+i)12+
=[(-+i)3]4+(-8+8i)
=1-8+8i=-7+8i。
10.复数z=,若z2+<0,求纯虚数A.
解:z==1-i,
∵a为纯虚数,设a=mi(m∈R,m≠0),
则z2+=(1-i)2+=-2i+
=-+(-2)i<0,
,∴m=4,∴a=4i。
11.定义运算=ad-bc,则满足=0的复数z所对应的点在第几象限?
解:结合=ad-bc可知
=z(1+i)-(1-i)(1+2i)=0,
∴z===2-i,
∴复数z所对应的点在第四象限。
备选例题
已知z1、z2∈C,z1+2z2∈R,且+=1,求证:z2-3z1为纯虚数。
思路探究:由题目条件推出(z2-3z1)2,再证明其小于0即可。
自主解答:∵+=1,
∴10z+5z=2z1·z2,
即z+4z+4z1·z2=-9z-z+6z1·z2,
也即-(z1+2z2)2=(3z1-z2)2.
∵z1+2z2∈R,z1≠0,z2≠0,
∴-(z1+2z2)2<0,
∴(3z1-z2)2<0,
∴(3z1-z2)2为负实数,
∴z2-3z1为纯虚数。
规律方法
1.证明z为纯虚数的方法:
(1)设z=a+bi(a,b∈R),证明a=0且b≠0;
(2)z2<0 z为纯虚数;
(3)z≠0,且z+=0 为纯虚数。
2.证明z∈R的方法:
(1)设z=a+bi(a、b∈R),证明b=0;
(2)z∈R z=;
(3)z∈R z2≥0;
(4)z∈R |z|2=z2.
备选变式
设z=a+bi(a、b∈R),若∈R,则a、b应满足什么条件?并说明理由。
解:=
=
=∈R,
∴b(a2+b2-1)=0,∴b=0或a2+b2=1.
小结
复数的概念
复数相等的充要条件
复数与复数分类
共轭复数
复数的模
复数的运算:复数的减法法则(a+bi)-(c+di)=(a-c)+(b-d)i复数减法的几何意义复平面上两点间的距离d=|z1-z2|复数的
加法法则(a+bi)+(c+di)=(a+c)+(b+d)i复数加法的几何意义复数的
乘法法则(a+bi)(c+di)=(ac-bd)+(ad+bc)i
复数的除法法则=+i(c+di≠0)
12 / 15
【教学目标】
1.知识与技能
理解并掌握复数的代数形式的乘法与除法运算法则,了解共轭复数的概念。
2.过程与方法
理解并掌握复数的除法运算实质是分母实数化问题,通过运算过程体会这一变形本质意图。
3.情感、态度与价值观
利用多项式除法和复数除法类比,知道事物之间是普遍联系的。通过复数除法运算,培养学生探索问题、分析问题、解决问题的能力。
【教学重难点】
重点:复数代数形式的乘除法运算。
难点:复数除法法则的运用。
【教学建议】
建议本节教学采用自学指导法,在学生自主学习的基础上可利用一下教学方法及手段完成本节教学:(1)类比分析法,通过对比多项式的乘法法则推出复数乘法法则。(2)归纳推理法,运用已有的多项式乘法法则和分母有理化及复数加减法的知识,通过归纳类比,推导复数除法法则。(3)合理、恰当地运用多媒体教学手段,将静态事物动态化,将抽象事物直观化,以突破教学难点。
【教学过程】
创设问题情境,引出问题,引导学生思考两个复数如何进行代数形式的乘法与除法运算。?让学生自主完成填一填,使学生进一步熟悉复数代数形式的乘法、除法运算的法则,及其满足的运算律。引导学生分析例题1的运算方法并求解,教师只需指导完善,解答疑惑并要求学生独立完成变式训练。由学生分组探究例题2解法,引导学生去发现in运算的周期性,及其应用方法。完成互动探究。
完成当堂双基达标,巩固所学知识及应用方法。并进行反馈矫正。归纳整理,进行课堂小结,整体认识本节所学知识,强调重点内容和规律方法。学生自主完成例题3变式训练,老师抽查完成情况,对出现问题及时指导。通过易错辨析纠正运算中出现的错误。?让学生自主分析例题3,老师适当点拨解题思路,学生分组讨论给出解法。老师组织解法展示,引导学生总结解题规律。
课标解读 1.掌握复数代数形式的乘、除运算。(重点)2.理解复数乘法的交换律、结合律和乘法对加法的分配律。(难点)3.理解共轭复数的概念。(易错点)
知识1 复数的乘法
问题导思:
1.如何规定两个复数相乘?
提示:两个复数相乘类似于多项式相乘,只要在所得结果中把i2换成-1,并且把实部与虚部分别合并即可。
2.复数乘法满足交换律、结合律以及乘法对加法的分配律吗?
提示:满足。
(1)设z1=a+bi,z2=c+di(a,b,c,d∈R),则
z1·z2=(a+bi)·(c+di)=(ac-bd)+(ad+bc)i。
(2)对于任意z1,z2,z3∈C,有
交换律 z1·z2=z2·z1
结合律 (z1·z2)·z3=z1·(z2·z3)
乘法对加法的分配律 z1(z2+z3)=z1z2+z1z3
知识2 复数的除法与共轭复数
问题导思:
如何规定两个复数z1=a+bi,z2=c+di(a,b,c,d∈R,c+di≠0)相除?
提示:===。
(1)z1=a+bi,z2=c+di(a,b,c,d为实数,c+di≠0),z1,z2进行除法运算时,通常先把(a+bi)÷(c+di)写成的形式再把分子与分母都乘以c-di化简后可得结果:+i。
(2)共轭复数
如果两个复数满足实部相等,虚部互为相反数时,称这两个复数为共轭复数,z的共轭复数用表示。即z=a+bi,则=a-bi。虚部不等于0的两个共轭复数也叫共轭虚数。
知识1 复数代数形式的乘除法运算
例1:(1)(2013·课标全国卷Ⅱ)设复数z满足(1-i)·z=2i,则z=( )
A.-1+i B.-1-i C.1+i D.1-i
(2)(2013·大纲全国卷)(1+i)3=( )
A.-8 B.8 C.-8i D.8i
(3)计算()6+=________。
思路探究:(1)先设出复数z=a+bi,然后运用复数相等的充要条件求出a,b的值。
(2)直接利用复数的乘法运算法则计算。
(3)先计算再乘方,且将的分母实数化后再合并。
自主解答:(1)设z=a+bi,则(1-i)(a+bi)=2i,即(a+b)+(b-a)i=2i。
根据复数相等的充要条件得解得
∴z=-1+i。故选A.
(2)原式=(1+i)(1+i)2=(1+i)(-2+2i)=-2+6i2=-8.
(3)法一:原式=6+
=i6+=-1+i。
法二 原式=6+
=i6+
=-1+i。
答案:(1)A (2)A (3)-1+i
规律方法
1.复数的乘法类比多项式相乘进行运算,复数除法要先写成分式形式后,再将分母实数化,注意最后结果要写成a+bi(a,b∈R)的形式。
2.记住以下结论可以提高运算速度
(1)(1+i)2=2i,(1-i)2=-2i;
(2)=-i,=i;
(3)=-i。
变式训练
计算:
(1)(1-i)2;
(2)(-+i)(+i)(1+i);
(3)。
解:(1)(1-i)2=1-2i+i2=-2i。
(2)(-+i)(+i)(1+i)
=(--i+i+i2)(1+i)
=(-+i-)(1+i)
=(-+i)(1+i)
=--i+i-
=-+i。
(3)===+i。
知识2 虚数单位i的幂的周期性及其应用
例2: (1)计算:+()2 013;
(2)若复数z=,求1+z+z2+…+z2 013的值。
思路探究:将式子进行适当的化简、变形,使之出现in的形式,然后再根据in的值的特点计算求解。
自主解答:(1)原式=+[()2]1 006·()
=i+()1 006·=i+i1 006·
=-+i
(2)1+z+z2+…+z2 013=,
而z====i,
所以1+z+z2+…+z2 013===1+i。
规律方法
1.要熟记in的取值的周期性,要注意根据式子的特点创造条件使之与in联系起来以便计算求值。
2.如果涉及数列求和问题,应先利用数列方法求和后再求解。
互动探究
在本例(2)中若z=i,求1+z+z2+…+z2 013的值。
解:由题意知
1+z+z2+…+z2 013=1+i+i2+…+i2 013
====1+i。
∴原式=1+i。
知识3 共轭复数的应用
例3:设z1,z2∈C,A=z1·+z2·,B=z1·+z2·,问A与B是否可以比较大小?为什么?
思路探究:设出z1,z2的代数形式→化简A,B→判断A,B是否同为实数→结论
自主解答:设z1=a+bi,
z2=c+di(a,b,c,d∈R),
则=a-bi,=c-di,
∴A=z1·+z2·
=(a+bi)(c-di)+(c+di)(a-bi)
=ac-adi+bci-bdi2+ac-bci+adi-bdi2
=2ac+2bd∈R,
B=z1·+z2·
=|z1|2+|z2|2
=a2+b2+c2+d2∈R,
∴A与B可以比较大小。
规律方法
1.z·=|z|2=||2是共轭复数的常用性质。
2.实数的共轭复数是它本身,即z∈R z=,利用此性质可以证明一个复数是实数。
3.若z≠0且z+=0,则z为纯虚数,利用此性质可证明一个复数是纯虚数。
变式训练
已知z∈C,为z的共轭复数,若z·-3i=1+3i,求z。
解:设z=a+bi(a,b∈R),则=a-bi(a,b∈R),
由题意得(a+bi)(a-bi)-3i(a-bi)=1+3i,
即a2+b2-3b-3ai=1+3i,
则有,
解得或,
所以z=-1或z=-1+3i。
典例:设复数z满足=i,则z=( )
A.-2+I B.-2-i
C.2-i D.2+i
错解:设复数z=a+bi(a,b∈R)满足=i,
所以1+2i=ai+B.
解得
所以z=2+i,故选D项。
答案:D
错因分析:将i2=-1当成i2=1来运算漏掉负号。
防范措施:在进行乘除法运算时,灵活运用i的性质,并注意一些重要结论的灵活应用。
正解:设复数z=a+bi(a,b∈R)满足=i,
所以1+2i=ai-B.
解得
所以z=2-i,故选C项。
答案:C
课堂小结
1.复数代数形式的乘除运算
(1)复数代数形式的乘法类似于多项式乘以多项式,复数的乘法满足交换律、结合律以及乘法对加法的分配律。
(2)在进行复数代数形式的除法运算时,通常先将除法写成分式的形式,再把分子、分母都乘以分母的共轭复数,化简后可得,类似于以前学习的分母有理化。
2.共轭复数的性质可以用来解决一些复数问题。
3.复数问题实数化思想。
复数问题实数化是解决复数问题的基本思想方法,其桥梁是设复数z=a+bi(a,b∈R),利用复数相等的充要条件转化。
当堂双基达标
1.(2012·北京高考)在复平面内,复数对应的点的坐标为( )
A.(1,3) B.(3,1)
C.(-1,3) D.(3,-1)
解析:===1+3i,
∴其对应点的坐标为(1,3),选A.
答案:A
2.(2013·安徽高考)设i是虚数单位,若复数a-(a∈R)是纯虚数,则a的值为( )
A.-3 B.-1
C.1 D.3
解析:因为a-=a-=a-=(a-3)-i,由纯虚数的定义,知a-3=0,所以a=3.
答案:D
3.若x-2+yi和3x-i互为共轭复数,则实数x=________,y=________。
解析:由题意得:
∴
答案:-1、1
4.计算:
(1)(1-i)(-+i)(1+i);
(2);
(3)(2-i)2.
解:(1)法一:(1-i)(-+i)(1+i)
=(-+i+i-i2)(1+i)
=(+i)(1+i)
=+i+i+i2
=-1+i。
法二:原式=(1-i)(1+i)(-+i)
=(1-i2)(-+i)
=2(-+i)
=-1+i。
(2)=
=
=
==i。
(3)(2-i)2=(2-i)(2-i)
=4-4i+i2
=3-4i。
课后知能训练
一、选择题
1.复数(2+i)2等于( )
A.3+4i B.5+4i
C.3+2i D.5+2i
解析:(2+i)2=4+4i+i2=4+4i-1=3+4i。故选A.
答案:A
2.i是虚数单位,复数=( )
A.1-i B.-1+i
C.1+i D.-1-i
解析:===1+i。
答案:C
3.若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
A.-4 B.-
C.4 D.
解析:∵(3-4i)z=|4+3i|,∴z====+i,∴z的虚部为。
答案:D
4.若z+=6,z·=10,则z=( )
A.1±3i B.3±i
C.3+i D.3-i
解析:设z=a+bi(a,b∈R),则=a-bi,
∴,解得a=3,b=±1,则z=3±i。
答案:B
5.(2013·湖北高考)在复平面内,复数z=(i为虚数单位)的共轭复数对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
解析:z===1+i,所以=1-i,故复数z的共轭复数对应的点位于第四象限。
答案:D
二、填空题
6.(2013·江苏高考)设z=(2-i)2(i为虚数单位),则复数z的模为________。
解析:z=(2-i)2=3-4i,所以|z|=|3-4i|==5.
答案:5
7.若=a+bi(a,b为实数,i为虚数单位),则a+b=________。
解析:=
=[(3-b)+(3+b)i]=+i。
∴解得∴a+b=3.
答案:3
8.当z=-时,z2 012+z2 014=________。
解析:z=-,∴z2==-i,
∴z2 012=(-i)2 012=1,
z2 014=(-i)2 014=-1,
∴z2 012+z2 014=1-1=0.
答案:0
三、解答题
9.计算下列各题:
(1)+-;
(2)(+i)5+()4+()7;
(3)(--i)12+()8.
解:(1)原式=[(1+i)2]3+[(1-i)2]3·-
=(2i)3·i+(-2i)3·(-i)-
=8+8-16-16i=-16i。
(2)(+i)5+()4+()7
=-i·()5·[(1+i)2]2·(1+i)+[]2+i7
=16(-1+i)--i
=-(16+)+(16-1)i。
(3)(--i)12+()8
=(-i)12·(--i)12+()8
=(-+i)12+
=[(-+i)3]4+(-8+8i)
=1-8+8i=-7+8i。
10.复数z=,若z2+<0,求纯虚数A.
解:z==1-i,
∵a为纯虚数,设a=mi(m∈R,m≠0),
则z2+=(1-i)2+=-2i+
=-+(-2)i<0,
,∴m=4,∴a=4i。
11.定义运算=ad-bc,则满足=0的复数z所对应的点在第几象限?
解:结合=ad-bc可知
=z(1+i)-(1-i)(1+2i)=0,
∴z===2-i,
∴复数z所对应的点在第四象限。
备选例题
已知z1、z2∈C,z1+2z2∈R,且+=1,求证:z2-3z1为纯虚数。
思路探究:由题目条件推出(z2-3z1)2,再证明其小于0即可。
自主解答:∵+=1,
∴10z+5z=2z1·z2,
即z+4z+4z1·z2=-9z-z+6z1·z2,
也即-(z1+2z2)2=(3z1-z2)2.
∵z1+2z2∈R,z1≠0,z2≠0,
∴-(z1+2z2)2<0,
∴(3z1-z2)2<0,
∴(3z1-z2)2为负实数,
∴z2-3z1为纯虚数。
规律方法
1.证明z为纯虚数的方法:
(1)设z=a+bi(a,b∈R),证明a=0且b≠0;
(2)z2<0 z为纯虚数;
(3)z≠0,且z+=0 为纯虚数。
2.证明z∈R的方法:
(1)设z=a+bi(a、b∈R),证明b=0;
(2)z∈R z=;
(3)z∈R z2≥0;
(4)z∈R |z|2=z2.
备选变式
设z=a+bi(a、b∈R),若∈R,则a、b应满足什么条件?并说明理由。
解:=
=
=∈R,
∴b(a2+b2-1)=0,∴b=0或a2+b2=1.
小结
复数的概念
复数相等的充要条件
复数与复数分类
共轭复数
复数的模
复数的运算:复数的减法法则(a+bi)-(c+di)=(a-c)+(b-d)i复数减法的几何意义复平面上两点间的距离d=|z1-z2|复数的
加法法则(a+bi)+(c+di)=(a+c)+(b+d)i复数加法的几何意义复数的
乘法法则(a+bi)(c+di)=(ac-bd)+(ad+bc)i
复数的除法法则=+i(c+di≠0)
12 / 15
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
