人教版A版(2019)课标高中数学必修二8.3简单几何体的表面积与体积 课件(共40张PPT)
文档属性
| 名称 | 人教版A版(2019)课标高中数学必修二8.3简单几何体的表面积与体积 课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1016.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 23:05:21 | ||
图片预览





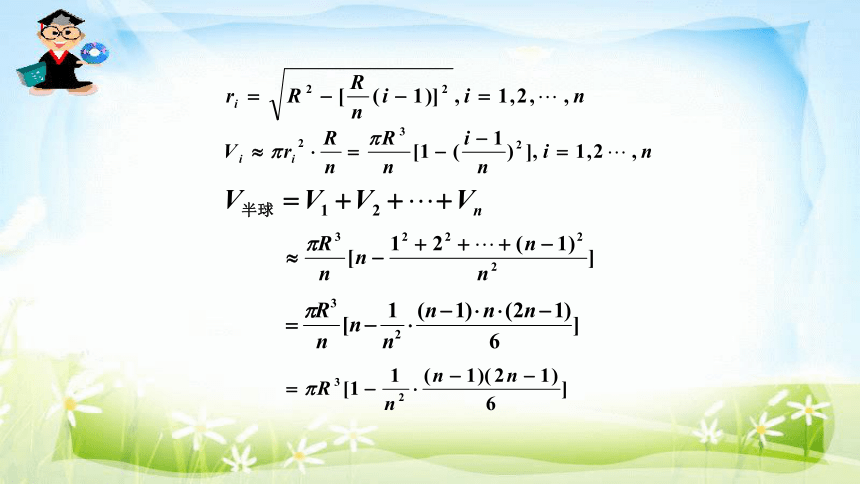
文档简介
(共40张PPT)
球的体积与表面积
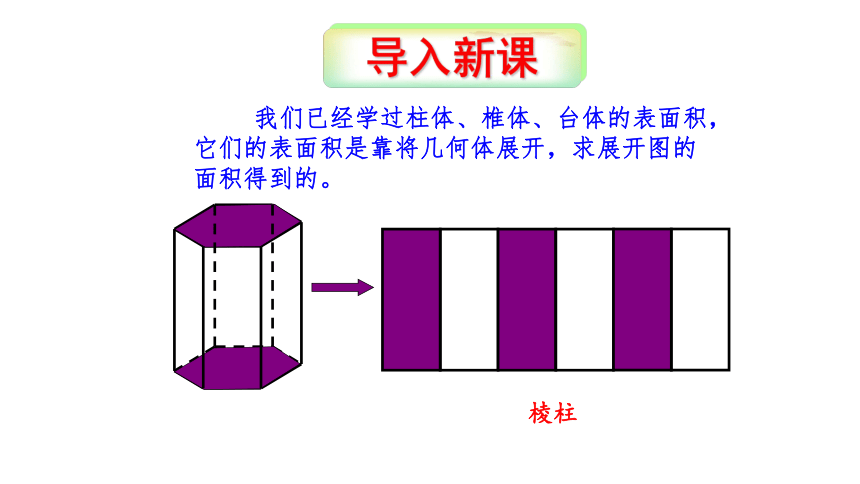
我们已经学过柱体、椎体、台体的表面积,它们的表面积是靠将几何体展开,求展开图的面积得到的。
导入新课
棱柱
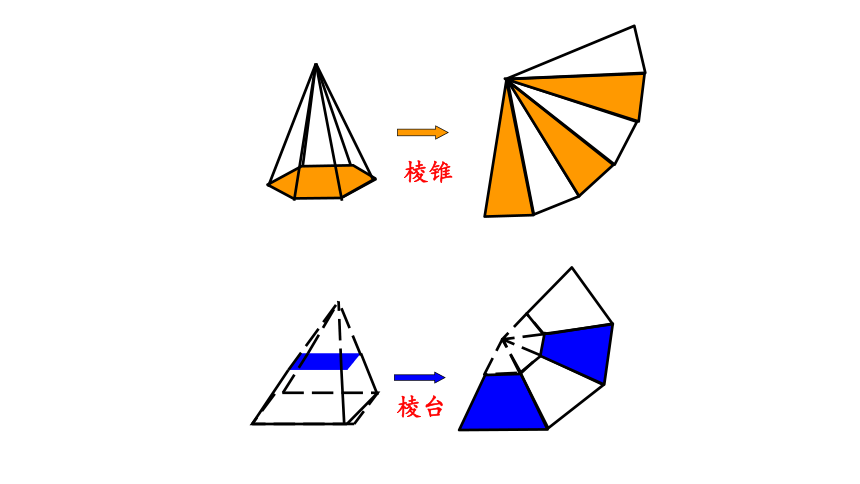
棱锥
棱台
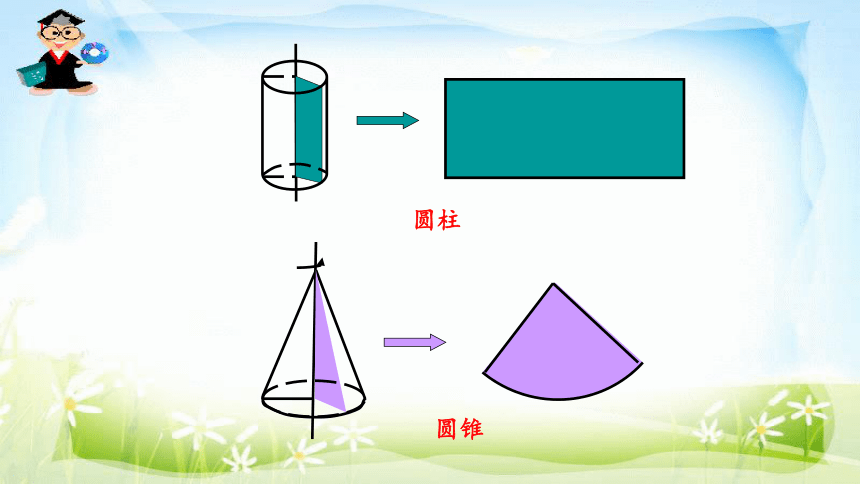
圆柱
圆锥
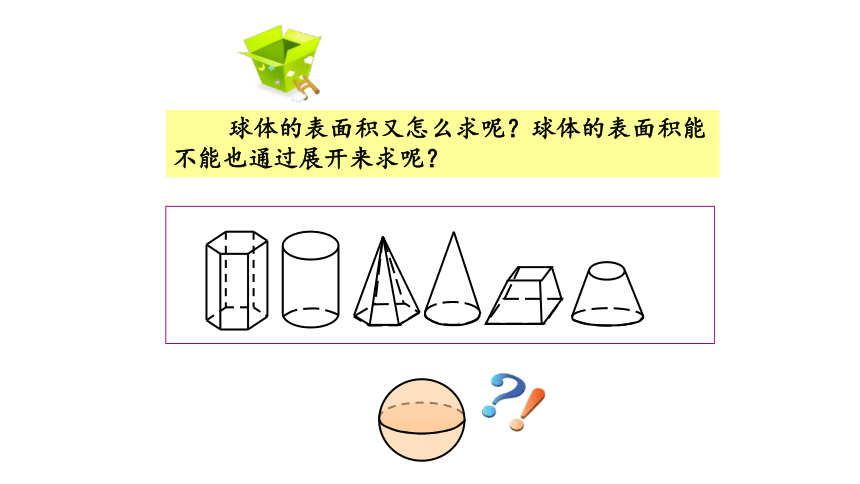
球体的表面积又怎么求呢?球体的表面积能不能也通过展开来求呢?
教学目标
知识与能力
通过对球的体积和面积公式的推导,了解推导过程中所用的基本数学思想方法:“分割——求和——化为准确和”。
能运用球的面积和体积公式灵活解决实际问题.
培养学生的空间思维能力和空间想象能力。
过程与方法
通过球的体积和面积公式的推导,从而得到一种推导球体积公式 和面积公式 的方法,即“分割求近似值,再由近似和转化为球的体积和面积”的方法,体现了极限思想。
情感态度与价值观
对球的体积和面积公式的推导方法有一定的了解,增强探索问题和解决问题的信心。
教学重难点
引导学生了解推导球的体积和面积公式所运用的基本思想方法。
推导体积和面积公式中空间想象能力的形成。
重点
难点
球体的体积的求法
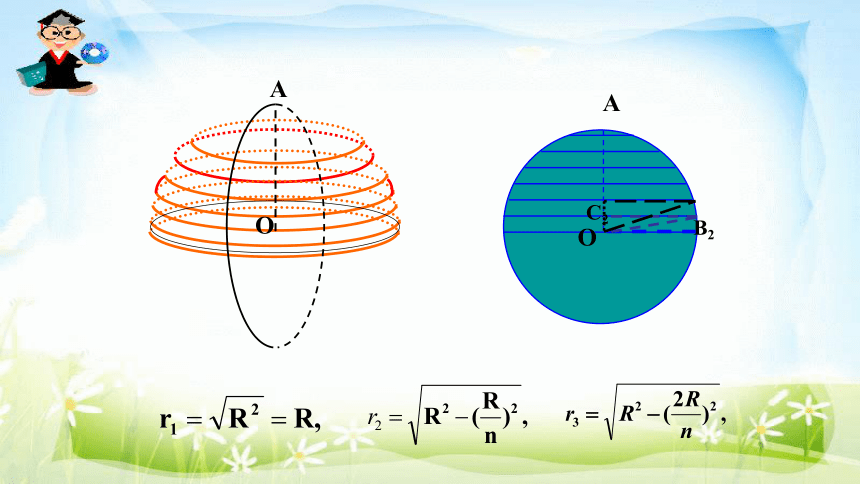
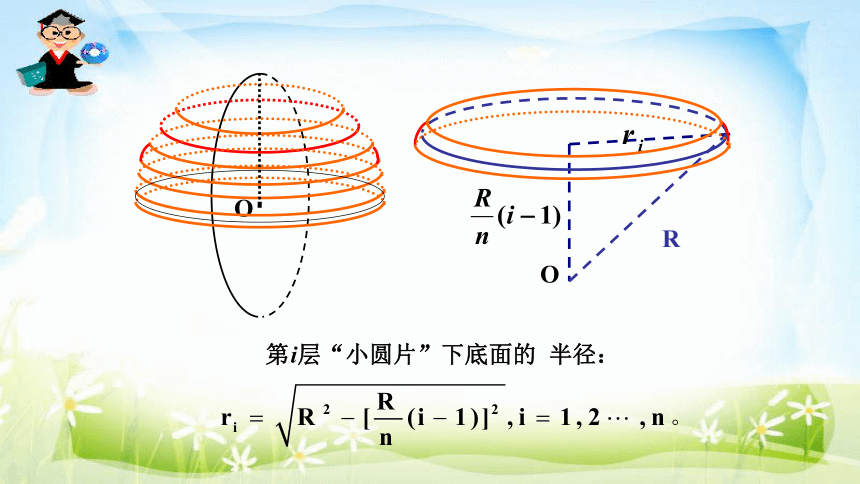
把半径OA作n等分,经过这些分点,用一组平行于底面的平面把半球切割成n层,每一层都是近似于圆柱形状的“小圆片”,这些小圆片的体积之和就是半球的体积。
探索与发现
1.球体的体积
A
O
B2
C2
A
O
O
R
O
半径是R的球的体积:
半径是R的球的体积:
设球的半径为R,它的体积只与半径R有关,是以R为自变量的函数。
思考
我们还能用哪些方法来求球体的体积呢?
h
排液法测球的体积
h
h
h
h
h
h
H
与排水法测球的体积与曹冲称象同理。
小球的体积等于它排开液体的体积。
球体的表面积的求法
球面不能展开成平面图形,所以求球的表面积无法用展开图求出,如何求球的表面积公式呢 与球的体积公式的推导方法一样,也可借助于这种极限思想方法来推导球的表面积公式。
分割
求近似和
化为准确和
探索与发现
2.球体的表面积
球面被分割成n个网格,表面积分别为:
则球的表面积:
O
O
第一步:分割
则球的体积为:
第二步:求近似和
由第一步得:
O
O
如果网格分的越细,则: “小锥体”就越接近小棱锥
O
第三步:化为准确和
半径是R的球的表面积:
设球的半径为R,它的表面积只与半径R有关,也是以R为自变量的函数。
思考
已知两个球体的半径之比,能得到它们的表面积之比,或所占体积之比吗?
半径之比为1:2,由 ,可知体积之比为1:8.同理,表面积之比为1:4。
如图:圆柱的底面直径与高都等于球的直径。
求证:
1、球的体积等于圆柱体积的 倍。
2、球的表面积等于圆柱的侧面积。
例四
R
证明:(1)设球的半径为R,则圆柱的底面半径为R,高为2R。
因为
所以,
(2)因为
所以,
课堂小结
半径是R的球的体积:
半径是R的球的表面积:
高考链接
1.(2009 全国Ⅱ)设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C,若圆C的面积等于 ,则球O的表面积等于______
【解析】设球的半径为R,截面圆的圆心为
,半径为r,则 , ,
直线OA与截面所成角为45°
为直线OA与截面所成的角,为45°即:
解得 ,故球O的表面积为
2.(2009 全国) 直三棱柱 的各顶点都在同一球面上,若
, ,则此球的表面积等于 。
【解析】本题考查球中截面圆的性质以及球与多面体的组合问题。在△ABC中,
故 .设△ABC的外接圆半径为
r,则 ,r=2。球的半径
所以,
课堂练习
4.若两球体积之比是1:2,则其表面积之比是______.
1.若球的表面积变为原来的2倍,则半径变为原来的___倍。
2.若球半径变为原来的2倍,则表面积变为原来的___倍.
3.若两球表面积之比为1:2,则其体积之比是______.
5. 一个四面体的所有的棱都为 ,四个顶点在同一球面上,则此球的表面积( )
·
●
●
●
●
O
●
●
B
D
C
A
解:设四面体为ABCD, 为其外接球心。
球半径为R,O为A在平面BCD上的射影,M为CD的中点.
M
连结B
R
A.
B.
C.
D.
A
7.一个正方体的顶点都在球面上,它的棱长是4cm,这个球的体积为___cm3。
8
8.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比_________。
6.球的直径伸长为原来的2倍,体积变为原来的_倍.
11.将半径为1和2的两个铅球,熔成一个大铅球,那么
这个大铅球的表面积是________。
9.长方体的共顶点的三个侧面积分别为 ,
则它的外接球的表面积为_______。
10.若两球表面积之差为48π ,它们大圆周长之和为12π ,则两球的直径之差为________。
习题答案
1. 8倍.
2.
3.104
球的体积与表面积
我们已经学过柱体、椎体、台体的表面积,它们的表面积是靠将几何体展开,求展开图的面积得到的。
导入新课
棱柱
棱锥
棱台
圆柱
圆锥
球体的表面积又怎么求呢?球体的表面积能不能也通过展开来求呢?
教学目标
知识与能力
通过对球的体积和面积公式的推导,了解推导过程中所用的基本数学思想方法:“分割——求和——化为准确和”。
能运用球的面积和体积公式灵活解决实际问题.
培养学生的空间思维能力和空间想象能力。
过程与方法
通过球的体积和面积公式的推导,从而得到一种推导球体积公式 和面积公式 的方法,即“分割求近似值,再由近似和转化为球的体积和面积”的方法,体现了极限思想。
情感态度与价值观
对球的体积和面积公式的推导方法有一定的了解,增强探索问题和解决问题的信心。
教学重难点
引导学生了解推导球的体积和面积公式所运用的基本思想方法。
推导体积和面积公式中空间想象能力的形成。
重点
难点
球体的体积的求法
把半径OA作n等分,经过这些分点,用一组平行于底面的平面把半球切割成n层,每一层都是近似于圆柱形状的“小圆片”,这些小圆片的体积之和就是半球的体积。
探索与发现
1.球体的体积
A
O
B2
C2
A
O
O
R
O
半径是R的球的体积:
半径是R的球的体积:
设球的半径为R,它的体积只与半径R有关,是以R为自变量的函数。
思考
我们还能用哪些方法来求球体的体积呢?
h
排液法测球的体积
h
h
h
h
h
h
H
与排水法测球的体积与曹冲称象同理。
小球的体积等于它排开液体的体积。
球体的表面积的求法
球面不能展开成平面图形,所以求球的表面积无法用展开图求出,如何求球的表面积公式呢 与球的体积公式的推导方法一样,也可借助于这种极限思想方法来推导球的表面积公式。
分割
求近似和
化为准确和
探索与发现
2.球体的表面积
球面被分割成n个网格,表面积分别为:
则球的表面积:
O
O
第一步:分割
则球的体积为:
第二步:求近似和
由第一步得:
O
O
如果网格分的越细,则: “小锥体”就越接近小棱锥
O
第三步:化为准确和
半径是R的球的表面积:
设球的半径为R,它的表面积只与半径R有关,也是以R为自变量的函数。
思考
已知两个球体的半径之比,能得到它们的表面积之比,或所占体积之比吗?
半径之比为1:2,由 ,可知体积之比为1:8.同理,表面积之比为1:4。
如图:圆柱的底面直径与高都等于球的直径。
求证:
1、球的体积等于圆柱体积的 倍。
2、球的表面积等于圆柱的侧面积。
例四
R
证明:(1)设球的半径为R,则圆柱的底面半径为R,高为2R。
因为
所以,
(2)因为
所以,
课堂小结
半径是R的球的体积:
半径是R的球的表面积:
高考链接
1.(2009 全国Ⅱ)设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C,若圆C的面积等于 ,则球O的表面积等于______
【解析】设球的半径为R,截面圆的圆心为
,半径为r,则 , ,
直线OA与截面所成角为45°
为直线OA与截面所成的角,为45°即:
解得 ,故球O的表面积为
2.(2009 全国) 直三棱柱 的各顶点都在同一球面上,若
, ,则此球的表面积等于 。
【解析】本题考查球中截面圆的性质以及球与多面体的组合问题。在△ABC中,
故 .设△ABC的外接圆半径为
r,则 ,r=2。球的半径
所以,
课堂练习
4.若两球体积之比是1:2,则其表面积之比是______.
1.若球的表面积变为原来的2倍,则半径变为原来的___倍。
2.若球半径变为原来的2倍,则表面积变为原来的___倍.
3.若两球表面积之比为1:2,则其体积之比是______.
5. 一个四面体的所有的棱都为 ,四个顶点在同一球面上,则此球的表面积( )
·
●
●
●
●
O
●
●
B
D
C
A
解:设四面体为ABCD, 为其外接球心。
球半径为R,O为A在平面BCD上的射影,M为CD的中点.
M
连结B
R
A.
B.
C.
D.
A
7.一个正方体的顶点都在球面上,它的棱长是4cm,这个球的体积为___cm3。
8
8.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比_________。
6.球的直径伸长为原来的2倍,体积变为原来的_倍.
11.将半径为1和2的两个铅球,熔成一个大铅球,那么
这个大铅球的表面积是________。
9.长方体的共顶点的三个侧面积分别为 ,
则它的外接球的表面积为_______。
10.若两球表面积之差为48π ,它们大圆周长之和为12π ,则两球的直径之差为________。
习题答案
1. 8倍.
2.
3.104
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
