6.4 平面向量的应用 教案
文档属性
| 名称 | 6.4 平面向量的应用 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 444.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 10:03:17 | ||
图片预览




文档简介
平面向量的应用
【第一课时】
教学重难点 教学目标 核心素养
向量在平面几何中的应用 会用向量方法解决平面几何中的平行、 垂直、长度、夹角等问题 数学建模、逻辑推理
向量在物理中的应用 会用向量方法解决物理中的速度、力学问题 数学建模、数学运算
【教学过程】
一、问题导入
预习教材内容,思考以下问题:
1.利用向量可以解决哪些常见的几何问题?
2.如何用向量方法解决物理问题?
二、新知探究
探究点1:
向量在几何中的应用
角度一:平面几何中的垂直问题
例1:如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
证明:法一:设=a,=b,
则|a|=|b|,a·b=0,
又=+=-a+b,=+=b+a,
所以·=·=-a2-a·b+b2=-|a|2+|b|2=0.
故⊥,即AF⊥DE.
法二:如图,建立平面直角坐标系,设正方形的边长为2,则A(0,0),D(0,2),E(1,0),F(2,1),=(2,1),=(1,-2).
因为·=(2,1)·(1,-2)=2-2=0,
所以⊥,即AF⊥DE.
角度二:平面几何中的平行(或共线)问题
:如图,点O是平行四边形ABCD的中心,E,F分别在边CD,AB上,且==.求证:点E,O,F在同一直线上.
证明:设=m,=n,
由==,知E,F分别是CD,AB的三等分点,
所以=+=+
=-m+(m+n)=m+n,
=+=+
=(m+n)-m=m+n.
所以=.
又O为和的公共点,故点E,O,F在同一直线上.
角度三:平面几何中的长度问题
:如图,平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2,求对角线AC的长.
解:设=a,=b,则=a-b,=a+b,
而||=|a-b|====2,
所以5-2a·b=4,所以a·b=,又||2=|a+b|2=a2+2a·b+b2=1+4+2a·b=6,所以||=,即AC=.
用向量方法解决平面几何问题的步骤
向量在物理中的应用
:(1)在长江南岸某渡口处,江水以12.5 km/h的速度向东流,渡船的速度为25 km/h.渡船要垂直地渡过长江,其航向应如何确定?
(2)已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0),求F1,F2分别对质点所做的功.
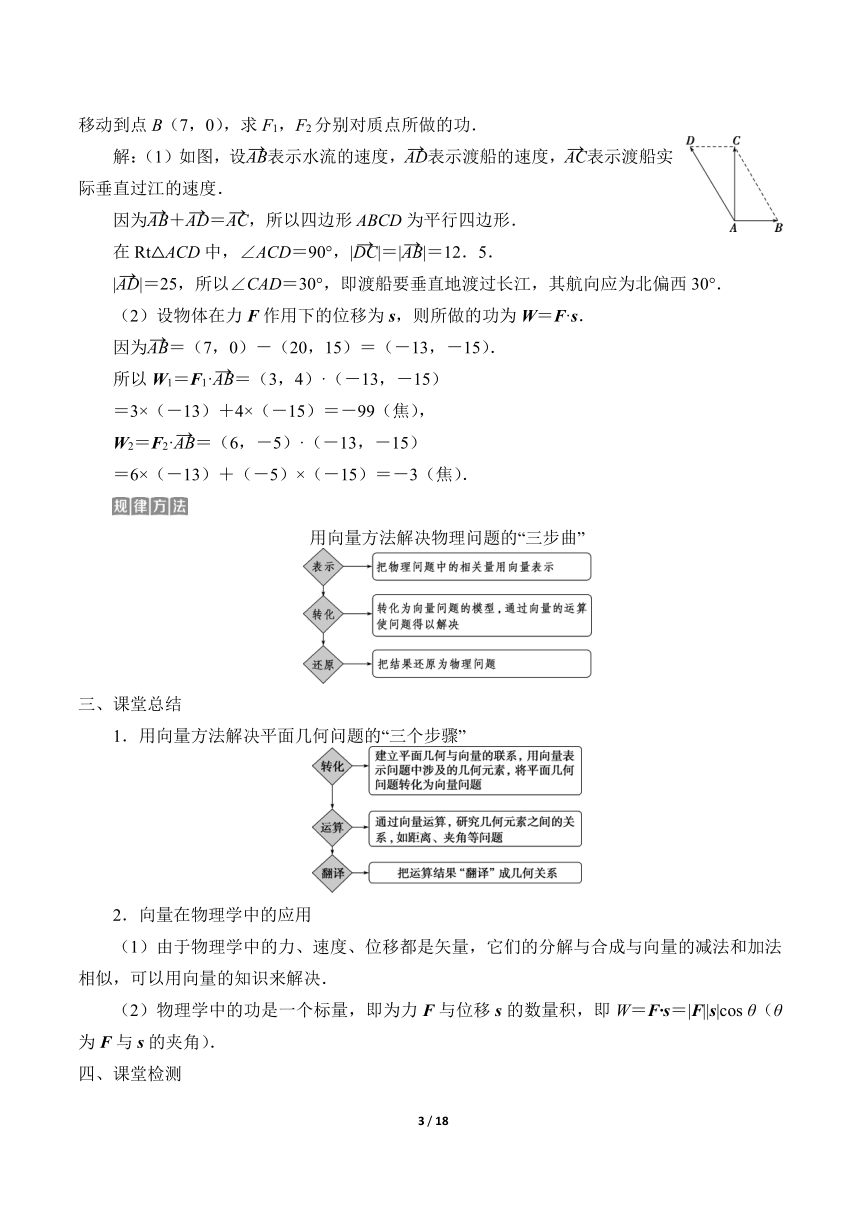
解:(1)如图,设表示水流的速度,表示渡船的速度,表示渡船实际垂直过江的速度.
因为+=,所以四边形ABCD为平行四边形.
在Rt△ACD中,∠ACD=90°,||=||=12.5.
||=25,所以∠CAD=30°,即渡船要垂直地渡过长江,其航向应为北偏西30°.
(2)设物体在力F作用下的位移为s,则所做的功为W=F·s.
因为=(7,0)-(20,15)=(-13,-15).
所以W1=F1·=(3,4)·(-13,-15)
=3×(-13)+4×(-15)=-99(焦),
W2=F2·=(6,-5)·(-13,-15)
=6×(-13)+(-5)×(-15)=-3(焦).
用向量方法解决物理问题的“三步曲”
三、课堂总结
1.用向量方法解决平面几何问题的“三个步骤”
2.向量在物理学中的应用
(1)由于物理学中的力、速度、位移都是矢量,它们的分解与合成与向量的减法和加法相似,可以用向量的知识来解决.
(2)物理学中的功是一个标量,即为力F与位移s的数量积,即W=F·s=|F||s|cos θ(θ为F与s的夹角).
四、课堂检测
1.河水的流速为2 m/s,一艘小船以垂直于河岸方向10 m/s的速度驶向对岸,则小船在静水中的速度大小为( )
A.10 m/s B.2 m/s
C.4 m/s D.12 m/s
解析:选B.由题意知|v水|=2 m/s,|v船|=10 m/s,作出示意图如图.
所以小船在静水中的速度大小
|v|==2(m/s).
2.已知三个力f1=(-2,-1),f2=(-3,2),f3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,再加上一个力f4,则f4=( )
A.(-1,-2) B.(1,-2)
C.(-1,2) D.(1,2)
解析:选D.由物理知识知f1+f2+f3+f4=0,故f4=-(f1+f2+f3)=(1,2).
3.设P,Q分别是梯形ABCD的对角线AC与BD的中点,AB∥DC,试用向量证明:PQ∥AB.
证明:设=λ(λ>0且λ≠1),因为=-=+-=+(-)
=+[(-)-(+)]
=+(-)
=(+)=(-λ+1),
所以∥,又P,Q,A,B四点不共线,所以PQ∥AB.
【第二课时】
教学重难点 教学目标 核心素养
余弦定理 了解余弦定理的推导过程 逻辑推理
余弦定理的推论 掌握余弦定理的几种变形公式及应用 数学运算
三角形的元素及解三角形 能利用余弦定理求解三角形的边、角等问题 数学运算
【教学过程】
一、问题导入
预习教材内容,思考以下问题:
1.余弦定理的内容是什么?
2.余弦定理有哪些推论?
二、新知探究
已知两边及一角解三角形
:(1)(2018·高考全国卷Ⅱ)在△ABC中,cos=,BC=1,AC=5,则AB=( )
A.4 B.
C. D.2
(2)已知△ABC的内角A,B,C的对边分别为a,b,c,a=,c=2,cos A=,则b=( )
A. B.
C.2 D.3
解析:(1)因为cos C=2cos2 -1=2×-1=-,所以由余弦定理,得AB2=AC2+BC2-2AC·BCcos C=25+1-2×5×1×=32,所以AB=4,故选A.
(2)由余弦定理得5=22+b2-2×2bcos A,
因为cos A=,所以3b2-8b-3=0,
所以b=3.故选D.
答案:(1)A
(2)D
互动探究:
变条件:将本例(2)中的条件“a=,c=2,cos A=”改为“a=2,c=2,cos A=”,求b为何值?
解:由余弦定理得:
a2=b2+c2-2bccos A,
所以22=b2+(2)2-2×b×2×,
即b2-6b+8=0,解得b=2或b=4.
规律方法:
解决“已知两边及一角”解三角问题的步骤
(1)用余弦定理列出关于第三边的等量关系建立方程,运用解方程的方法求出此边长.
(2)再用余弦定理和三角形内角和定理求出其他两角.
探究点2:
已知三边(三边关系)解三角形
:(1)在△ABC中,已知a=3,b=5,c=,则最大角与最小角的和为( )
A.90° B.120°
C.135° D.150°
(2)在△ABC中,若(a+c)(a-c)=b(b-c),则A等于( )
A.90° B.60°
C.120° D.150°
解析:(1)在△ABC中,因为a=3,b=5,c=,
所以最大角为B,最小角为A,
所以cos C===,所以C=60°,所以A+B=120°,所以△ABC中的最大角与最小角的和为120°.故选B.
(2)因为(a+c)(a-c)=b(b-c),所以b2+c2-a2=bc,所以cos A==.因为A∈(0°,180°),所以A=60°.
答案:(1)B
(2)B
已知三角形的三边解三角形的方法
先利用余弦定理的推论求出一个角的余弦,从而求出第一个角;再利用余弦定理的推论求出第二个角;最后利用三角形的内角和定理求出第三个角.
注意:若已知三角形三边的比例关系,常根据比例的性质引入k,从而转化为已知三边求解.
探究点3:
判断三角形的形状
:在△ABC中,若b2sin2C+c2sin2B=2bccos Bcos C,试判断△ABC的形状.
解:将已知等式变形为
b2(1-cos2C)+c2(1-cos2B)=2bccos Bcos C.
由余弦定理并整理,得
b2+c2-b2-c2
=2bc××,
所以b2+c2===a2.
所以A=90°.所以△ABC是直角三角形.
规律方法:
(1)利用余弦定理判断三角形形状的两种途径
①化边的关系:将条件中的角的关系,利用余弦定理化为边的关系,再变形条件判断.
②化角的关系:将条件转化为角与角之间的关系,通过三角变换得出关系进行判断.
(2)判断三角形时经常用到以下结论
①△ABC为直角三角形 a2=b2+c2或c2=a2+b2或b2=a2+c2.
②△ABC为锐角三角形 a2+b2>c2,且b2+c2>a2,且c2+a2>b2.
③△ABC为钝角三角形 a2+b2<c2或b2+c2<a2或c2+a2<b2.
④若sin 2A=sin 2B,则A=B或A+B=.
三、课堂总结
1.余弦定理
文字语言 三角形中任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍
符号语言 a2=b2+c2-2bccos_A b2=a2+c2-2accos_B c2=a2+b2-2abcos_C
2.余弦定理的推论
cos A=;
cos B=;
cos C=.
3.三角形的元素与解三角形
(1)三角形的元素
三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.
(2)解三角形
已知三角形的几个元素求其他元素的过程叫做解三角形.
四、课堂检测
1.在△ABC中,已知a=5,b=7,c=8,则A+C=( )
A.90° B.120°
C.135° D.150°
解析:选B.cos B===.
所以B=60°,所以A+C=120°.
2.在△ABC中,已知(a+b+c)(b+c-a)=3bc,则角A等于( )
A.30° B.60°
C.120° D.150°
解析:选B.因为(b+c)2-a2=b2+c2+2bc-a2=3bc,
所以b2+c2-a2=bc,
所以cosA==,所以A=60°.
3.若△ABC的内角A,B,C所对的边a,b,c满足(a+b)2-c2=4,且C=60°,则ab=________.
解析:因为C=60°,所以c2=a2+b2-2abcos 60°,
即c2=a2+b2-ab.①
又因为(a+b)2-c2=4,
所以c2=a2+b2+2ab-4.②
由①②知-ab=2ab-4,所以ab=.
答案:
4.在△ABC中,acosA+bcosB=ccosC,试判断△ABC的形状.
解:由余弦定理知cos A=,cos B=,cos C=,代入已知条件得a·+b·+c·=0,
通分得a2(b2+c2-a2)+b2(a2+c2-b2)+c2(c2-a2-b2)=0,
展开整理得(a2-b2)2=c4.
所以a2-b2=±c2,即a2=b2+c2或b2=a2+c2.
根据勾股定理知△ABC是直角三角形.
【第三课时】
教学重难点 教学目标 核心素养
正弦定理 通过对任意三角形边长和角度关系的探索,掌握正弦 定理的内容及其证明方法 逻辑推理
【教学过程】
一、问题导入
预习教材内容,思考以下问题:
1.在直角三角形中,边与角之间的关系是什么?
2.正弦定理的内容是什么?
二、新知探究
已知两角及一边解三角形
:在△ABC中,已知c=10,A=45°,C=30°,解这个三角形.
【解】因为A=45°,C=30°,所以B=180°-(A+C)=105°.
由=得a==10×=10.
因为sin 75°=sin(30°+45°)=sin 30°cos 45°+cos 30°sin 45°=,所以b===20×=5+5.
已知三角形的两角和任一边解三角形的思路
(1)若所给边是已知角的对边时,可由正弦定理求另一角所对的边,再由三角形内角和定理求出第三个角.
(2)若所给边不是已知角的对边时,先由三角形内角和定理求出第三个角,再由正弦定理求另外两边.
已知两边及其中一边的对角解三角形
已知△ABC中的下列条件,解三角形:
(1)a=10,b=20,A=60°;
(2)a=2,c=,C=.
解:(1)因为=,
所以sin B===>1,
所以三角形无解.
(2)因为=,所以sin A==.
因为c>a,所以C>A.所以A=.
所以B=,b= ==+1.
互动探究:
变条件:若本例(2)中C=改为A=,其他条件不变,求C,B, b.
解:因为=,所以sin C==.
所以C=或.
当C=时,B=,b==+1.
当C=时,B=,b==-1.
(1)已知两边及其中一边的对角解三角形的思路
①首先由正弦定理求出另一边对角的正弦值;
②如果已知的角为大边所对的角时,由三角形中大边对大角,大角对大边的法则能判断另一边所对的角为锐角,由正弦值可求锐角;
③如果已知的角为小边所对的角时,则不能判断另一边所对的角为锐角,这时由正弦值可求两个角,要分类讨论.
(2)已知两边及其中一边的对角判断三角形解的个数的方法
①应用三角形中大边对大角的性质以及正弦函数的值域判断解的个数;
②在△ABC中,已知a,b和A,以点C为圆心,以边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形解的个数,解的个数见下表:
A为钝角 A为直角 A为锐角
a>b 一解 一解 一解
a=b 无解 无解 一解
absin A 两解
a=bsin A 一解
a判断三角形的形状
:已知在△ABC中,角A,B所对的边分别是a和b,若acos B=bcos A,则△ABC一定是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
解析:由正弦定理得:acos B=bcos A sin Acos B=sin Bcos A sin(A-B)=0,由于-π<A-B<π,故必有A-B=0,A=B,即△ABC为等腰三角形.
答案:A
互动探究:
变条件:若把本例条件变为“bsin B=csin C”,试判断△ABC的形状.
解:由bsin B=csin C可得sin2B=sin2C,因为三角形内角和为180°,
所以sin B=sin C.所以B=C.故△ABC为等腰三角形.
判断三角形形状的两种途径
注意:在两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.
三、课堂总结
1.正弦定理
条件 在△ABC中,角A,B,C所对的边分别为a,b,c
结论 ==
文字 叙述 在一个三角形中,各边和它所对角的正弦的比相等
■名师点拨
对正弦定理的理解
(1)适用范围:正弦定理对任意的三角形都成立.
(2)结构形式:分子为三角形的边长,分母为相应边所对角的正弦的连等式.
(3)揭示规律:正弦定理指出的是三角形中三条边与其对应角的正弦之间的一个关系式,它描述了三角形中边与角的一种数量关系.
2.正弦定理的变形
若R为△ABC外接圆的半径,则
(1)a=2Rsin A,b=2Rsin B,c=2Rsin C;
(2)sin A=,sin B=,sin C=;
(3)sin A∶sin B∶sin C=a∶b∶c;
(4)=2R.
四、课堂检测
1.(2019·辽宁沈阳铁路实验中学期中考试)在△ABC中,AB=2,AC=3,B=60°,则cos C=( )
A. B.
C. D.
解析:选B.由正弦定理,得=,即=,解得sin C=.因为AB<AC,所以C<B,所以cos C==.
2.在△ABC中,角A,B,C的对边分别为a,b,c,且A∶B∶C=1∶2∶3,则a∶b∶c=( )
A.1∶2∶3 B.3∶2∶1
C.2∶∶1 D.1∶∶2
解析:选D.在△ABC中,因为A∶B∶C=1∶2∶3,所以B=2A,C=3A,又A+B+C=180°,所以A=30°,B=60°,C=90°,所以a∶b∶c=sin A∶sin B∶sin C=sin 30°∶sin 60°∶sin 90°=1∶∶2.
3.在△ABC中,角A,B,C的对边分别是a,b,c,若c-acos B=(2a-b)cos A,则△ABC的形状是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
解析:选D.已知c-acos B=(2a-b)cos A,由正弦定理得sin C-sin Acos B=2sin Acos A-sin Bcos A,所以sin(A+B)-sin Acos B=2sin Acos A-sin Bcos A,化简得cos A(sin B-sin A)=0,所以cos A=0或sin B-sin A=0,则A=90°或A=B,故△ABC为等腰三角形或直角三角形.
【第四课时】
教学重难点 教学目标 核心素养
测量中的术语 理解测量中的基线等有关名词、术语的确切含义 直观想象
测量距离、高度、角度问题 会利用正、余弦定理解决生产实践中的有关距离、高度、角度等问题 数学建模
【教学过程】
一、问题导入
预习教材内容,思考以下问题:
1.什么是基线?
2.基线的长度与测量的精确度有什么关系?
3.利用正、余弦定理可解决哪些实际问题?
二、新知探究
测量距离问题
:海上A,B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B岛与C岛间的距离是________.
解析:如图,在△ABC中,∠C=180°-(∠B+∠A)=45°,
由正弦定理,可得=,
所以BC=×10=5(海里).
答案:5海里
变条件:在本例中,若“从B岛望C岛和A岛成75°的视角”改为“A,C两岛相距20海里”,其他条件不变,又如何求B岛与C岛间的距离呢?
解:由已知在△ABC中,AB=10,AC=20,∠BAC=60°,即已知两边和两边的夹角,利用余弦定理求解即可.
BC2=AB2+AC2-2AB·AC·cos 60°=102+202-2×10×20×=300.故BC=10.
即B,C间的距离为10海里.
测量距离问题的解题思路
求解测量距离问题的方法是:选择合适的辅助测量点,构造三角形,将问题转化为求某个三角形的边长问题,从而利用正、余弦定理求解.构造数学模型时,尽量把已知元素放在同一个三角形中.
测量高度问题
:如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=________m.
解析:由题意,在△ABC中,∠BAC=30°,∠ABC=180°-75°=105°,故∠ACB=45°.
又AB=600 m,故由正弦定理得=,
解得BC=300 m.在Rt△BCD中,CD=BC·tan 30°=300×=100(m).
答案:100
互动探究:
变问法:在本例条件下,汽车在沿直线AB方向行驶的过程中,若测得观察山顶D点的最大仰角为α,求tan α的值.
解:如图,过点C,作CE⊥AB,垂足为E,则∠DEC=α,由例题可知,
∠CBE=75°,BC=300,
所以CE=BC·sin∠CBE
=300sin 75°
=300×
=150+150.
所以tan α===.
测量高度问题的解题思路
高度的测量主要是一些底部不能到达或者无法直接测量的物体的高度问题.常用正弦定理或余弦定理计算出物体的顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.这类物体高度的测量是在与地面垂直的竖直平面内构造三角形或者在空间构造三棱锥,再依据条件利用正、余弦定理解其中的一个或者几个三角形,从而求出所需测量物体的高度.
测量角度问题
:岛A观察站发现在其东南方向有一艘可疑船只,正以每小时10海里的速度向东南方向航行(如图所示),观察站即刻通知在岛A正南方向B处巡航的海监船前往检查.接到通知后,海监船测得可疑船只在其北偏东75°方向且相距10海里的C处,随即以每小时10海里的速度前往拦截.
(1)问:海监船接到通知时,在距离岛A多少海里处?
(2)假设海监船在D处恰好追上可疑船只,求它的航行方向及其航行的时间.
解:(1)根据题意得∠BAC=45°,∠ABC=75°,BC=10,
所以∠ACB=180°-75°-45°=60°,
在△ABC中,由=,
得AB====5.
所以海监船接到通知时,在距离岛A 5 海里处.
(2)设海监船航行时间为t小时,则BD=10t,CD=10t,
又因为∠BCD=180°-∠ACB=180°-60°=120°,
所以BD2=BC2+CD2-2BC·CDcos 120°,
所以300t2=100+100t2-2×10×10t·,
所以2t2-t-1=0,
解得t=1或t=-(舍去).
所以CD=10,所以BC=CD,
所以∠CBD=(180°-120°)=30°,
所以∠ABD=75°+30°=105°.
所以海监船沿方位角105°航行,航行时间为1个小时.
(或海监船沿南偏东75°方向航行,航行时间为1个小时)
测量角度问题的基本思路
(1)测量角度问题的关键是在弄清题意的基础上,画出表示实际问题的图形,在图形中标出相关的角和距离.
(2)根据实际选择正弦定理或余弦定理解三角形,然后将解得的结果转化为实际问题的解.
三、课堂总结
1.基线
在测量过程中,我们把根据测量的需要而确定的线段叫做基线
实际测量中的有关名称、术语
名称 定义 图示
仰角 在同一铅垂平面内,视线在水平线上方时与水平线的夹角
俯角 在同一铅垂平面内,视线在水平线下方时与水平线的夹角
方向角 从指定方向线到目标方向线的水平角(指定方向线是指正北或正南或正东或正西,方向角小于90°) 南偏西60°(指以正南方向为始边,转向目标方向线形成的角)
方位角 从正北的方向线按顺时针到目标方向线所转过的水平角
四、课堂检测
1.若P在Q的北偏东44°50′方向上,则Q在P的( )
A.东偏北45°10′方向上 B.东偏北45°50′方向上
C.南偏西44°50′方向上 D.西偏南45°50′方向上
解析:选C.如图所示.
2.如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=200米,点C位于BD上,则山高AB等于( )
A.100米 B.50(+1)米
C.100(+1)米 D.200米
解析:选C.设AB=x米,在Rt△ACB中,∠ACB=45°,
所以BC=AB=x.
在Rt△ABD中,∠D=30°,则BD=AB=x.
因为BD-BC=CD,所以x-x=200,
解得x=100(+1).故选C.
3.已知台风中心位于城市A东偏北α(α为锐角)度的150公里处,以v公里/小时沿正西方向快速移动,2.5小时后到达距城市A西偏北β(β为锐角)度的200公里处,若cos α=cos β,则v=( )
A.60 B.80
C.100 D.125
解析:选C.画出图象如图所示,由余弦定理得(2.5v)2=2002+1502+2×200×150cos(α+β)①,由正弦定理得=,所以sin α=sin β.又cos α= cos β,sin2 α+cos2 α=1,解得sin β=,故cos β=,sin α=,cos α=,故cos(α+β)=-=0,代入①解得v=100.
4.某巡逻艇在A处发现在北偏东45°距A处8海里处有一走私船,正沿南偏东75°的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以12海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇的航行方向.
解:设经过t小时在点C处刚好追上走私船,依题意:AC=12t,BC=12t,∠ABC=120°,
在△ABC中,由正弦定理得=,
所以sin∠BAC=,所以∠BAC=30°,
所以AB=BC=8=12t,解得t=,航行的方向为北偏东75°.
即巡逻艇最少经过小时可追到走私船,沿北偏东75°的方向航行.
1 / 18
【第一课时】
教学重难点 教学目标 核心素养
向量在平面几何中的应用 会用向量方法解决平面几何中的平行、 垂直、长度、夹角等问题 数学建模、逻辑推理
向量在物理中的应用 会用向量方法解决物理中的速度、力学问题 数学建模、数学运算
【教学过程】
一、问题导入
预习教材内容,思考以下问题:
1.利用向量可以解决哪些常见的几何问题?
2.如何用向量方法解决物理问题?
二、新知探究
探究点1:
向量在几何中的应用
角度一:平面几何中的垂直问题
例1:如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE.
证明:法一:设=a,=b,
则|a|=|b|,a·b=0,
又=+=-a+b,=+=b+a,
所以·=·=-a2-a·b+b2=-|a|2+|b|2=0.
故⊥,即AF⊥DE.
法二:如图,建立平面直角坐标系,设正方形的边长为2,则A(0,0),D(0,2),E(1,0),F(2,1),=(2,1),=(1,-2).
因为·=(2,1)·(1,-2)=2-2=0,
所以⊥,即AF⊥DE.
角度二:平面几何中的平行(或共线)问题
:如图,点O是平行四边形ABCD的中心,E,F分别在边CD,AB上,且==.求证:点E,O,F在同一直线上.
证明:设=m,=n,
由==,知E,F分别是CD,AB的三等分点,
所以=+=+
=-m+(m+n)=m+n,
=+=+
=(m+n)-m=m+n.
所以=.
又O为和的公共点,故点E,O,F在同一直线上.
角度三:平面几何中的长度问题
:如图,平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2,求对角线AC的长.
解:设=a,=b,则=a-b,=a+b,
而||=|a-b|====2,
所以5-2a·b=4,所以a·b=,又||2=|a+b|2=a2+2a·b+b2=1+4+2a·b=6,所以||=,即AC=.
用向量方法解决平面几何问题的步骤
向量在物理中的应用
:(1)在长江南岸某渡口处,江水以12.5 km/h的速度向东流,渡船的速度为25 km/h.渡船要垂直地渡过长江,其航向应如何确定?
(2)已知两恒力F1=(3,4),F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0),求F1,F2分别对质点所做的功.
解:(1)如图,设表示水流的速度,表示渡船的速度,表示渡船实际垂直过江的速度.
因为+=,所以四边形ABCD为平行四边形.
在Rt△ACD中,∠ACD=90°,||=||=12.5.
||=25,所以∠CAD=30°,即渡船要垂直地渡过长江,其航向应为北偏西30°.
(2)设物体在力F作用下的位移为s,则所做的功为W=F·s.
因为=(7,0)-(20,15)=(-13,-15).
所以W1=F1·=(3,4)·(-13,-15)
=3×(-13)+4×(-15)=-99(焦),
W2=F2·=(6,-5)·(-13,-15)
=6×(-13)+(-5)×(-15)=-3(焦).
用向量方法解决物理问题的“三步曲”
三、课堂总结
1.用向量方法解决平面几何问题的“三个步骤”
2.向量在物理学中的应用
(1)由于物理学中的力、速度、位移都是矢量,它们的分解与合成与向量的减法和加法相似,可以用向量的知识来解决.
(2)物理学中的功是一个标量,即为力F与位移s的数量积,即W=F·s=|F||s|cos θ(θ为F与s的夹角).
四、课堂检测
1.河水的流速为2 m/s,一艘小船以垂直于河岸方向10 m/s的速度驶向对岸,则小船在静水中的速度大小为( )
A.10 m/s B.2 m/s
C.4 m/s D.12 m/s
解析:选B.由题意知|v水|=2 m/s,|v船|=10 m/s,作出示意图如图.
所以小船在静水中的速度大小
|v|==2(m/s).
2.已知三个力f1=(-2,-1),f2=(-3,2),f3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,再加上一个力f4,则f4=( )
A.(-1,-2) B.(1,-2)
C.(-1,2) D.(1,2)
解析:选D.由物理知识知f1+f2+f3+f4=0,故f4=-(f1+f2+f3)=(1,2).
3.设P,Q分别是梯形ABCD的对角线AC与BD的中点,AB∥DC,试用向量证明:PQ∥AB.
证明:设=λ(λ>0且λ≠1),因为=-=+-=+(-)
=+[(-)-(+)]
=+(-)
=(+)=(-λ+1),
所以∥,又P,Q,A,B四点不共线,所以PQ∥AB.
【第二课时】
教学重难点 教学目标 核心素养
余弦定理 了解余弦定理的推导过程 逻辑推理
余弦定理的推论 掌握余弦定理的几种变形公式及应用 数学运算
三角形的元素及解三角形 能利用余弦定理求解三角形的边、角等问题 数学运算
【教学过程】
一、问题导入
预习教材内容,思考以下问题:
1.余弦定理的内容是什么?
2.余弦定理有哪些推论?
二、新知探究
已知两边及一角解三角形
:(1)(2018·高考全国卷Ⅱ)在△ABC中,cos=,BC=1,AC=5,则AB=( )
A.4 B.
C. D.2
(2)已知△ABC的内角A,B,C的对边分别为a,b,c,a=,c=2,cos A=,则b=( )
A. B.
C.2 D.3
解析:(1)因为cos C=2cos2 -1=2×-1=-,所以由余弦定理,得AB2=AC2+BC2-2AC·BCcos C=25+1-2×5×1×=32,所以AB=4,故选A.
(2)由余弦定理得5=22+b2-2×2bcos A,
因为cos A=,所以3b2-8b-3=0,
所以b=3.故选D.
答案:(1)A
(2)D
互动探究:
变条件:将本例(2)中的条件“a=,c=2,cos A=”改为“a=2,c=2,cos A=”,求b为何值?
解:由余弦定理得:
a2=b2+c2-2bccos A,
所以22=b2+(2)2-2×b×2×,
即b2-6b+8=0,解得b=2或b=4.
规律方法:
解决“已知两边及一角”解三角问题的步骤
(1)用余弦定理列出关于第三边的等量关系建立方程,运用解方程的方法求出此边长.
(2)再用余弦定理和三角形内角和定理求出其他两角.
探究点2:
已知三边(三边关系)解三角形
:(1)在△ABC中,已知a=3,b=5,c=,则最大角与最小角的和为( )
A.90° B.120°
C.135° D.150°
(2)在△ABC中,若(a+c)(a-c)=b(b-c),则A等于( )
A.90° B.60°
C.120° D.150°
解析:(1)在△ABC中,因为a=3,b=5,c=,
所以最大角为B,最小角为A,
所以cos C===,所以C=60°,所以A+B=120°,所以△ABC中的最大角与最小角的和为120°.故选B.
(2)因为(a+c)(a-c)=b(b-c),所以b2+c2-a2=bc,所以cos A==.因为A∈(0°,180°),所以A=60°.
答案:(1)B
(2)B
已知三角形的三边解三角形的方法
先利用余弦定理的推论求出一个角的余弦,从而求出第一个角;再利用余弦定理的推论求出第二个角;最后利用三角形的内角和定理求出第三个角.
注意:若已知三角形三边的比例关系,常根据比例的性质引入k,从而转化为已知三边求解.
探究点3:
判断三角形的形状
:在△ABC中,若b2sin2C+c2sin2B=2bccos Bcos C,试判断△ABC的形状.
解:将已知等式变形为
b2(1-cos2C)+c2(1-cos2B)=2bccos Bcos C.
由余弦定理并整理,得
b2+c2-b2-c2
=2bc××,
所以b2+c2===a2.
所以A=90°.所以△ABC是直角三角形.
规律方法:
(1)利用余弦定理判断三角形形状的两种途径
①化边的关系:将条件中的角的关系,利用余弦定理化为边的关系,再变形条件判断.
②化角的关系:将条件转化为角与角之间的关系,通过三角变换得出关系进行判断.
(2)判断三角形时经常用到以下结论
①△ABC为直角三角形 a2=b2+c2或c2=a2+b2或b2=a2+c2.
②△ABC为锐角三角形 a2+b2>c2,且b2+c2>a2,且c2+a2>b2.
③△ABC为钝角三角形 a2+b2<c2或b2+c2<a2或c2+a2<b2.
④若sin 2A=sin 2B,则A=B或A+B=.
三、课堂总结
1.余弦定理
文字语言 三角形中任何一边的平方,等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍
符号语言 a2=b2+c2-2bccos_A b2=a2+c2-2accos_B c2=a2+b2-2abcos_C
2.余弦定理的推论
cos A=;
cos B=;
cos C=.
3.三角形的元素与解三角形
(1)三角形的元素
三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.
(2)解三角形
已知三角形的几个元素求其他元素的过程叫做解三角形.
四、课堂检测
1.在△ABC中,已知a=5,b=7,c=8,则A+C=( )
A.90° B.120°
C.135° D.150°
解析:选B.cos B===.
所以B=60°,所以A+C=120°.
2.在△ABC中,已知(a+b+c)(b+c-a)=3bc,则角A等于( )
A.30° B.60°
C.120° D.150°
解析:选B.因为(b+c)2-a2=b2+c2+2bc-a2=3bc,
所以b2+c2-a2=bc,
所以cosA==,所以A=60°.
3.若△ABC的内角A,B,C所对的边a,b,c满足(a+b)2-c2=4,且C=60°,则ab=________.
解析:因为C=60°,所以c2=a2+b2-2abcos 60°,
即c2=a2+b2-ab.①
又因为(a+b)2-c2=4,
所以c2=a2+b2+2ab-4.②
由①②知-ab=2ab-4,所以ab=.
答案:
4.在△ABC中,acosA+bcosB=ccosC,试判断△ABC的形状.
解:由余弦定理知cos A=,cos B=,cos C=,代入已知条件得a·+b·+c·=0,
通分得a2(b2+c2-a2)+b2(a2+c2-b2)+c2(c2-a2-b2)=0,
展开整理得(a2-b2)2=c4.
所以a2-b2=±c2,即a2=b2+c2或b2=a2+c2.
根据勾股定理知△ABC是直角三角形.
【第三课时】
教学重难点 教学目标 核心素养
正弦定理 通过对任意三角形边长和角度关系的探索,掌握正弦 定理的内容及其证明方法 逻辑推理
【教学过程】
一、问题导入
预习教材内容,思考以下问题:
1.在直角三角形中,边与角之间的关系是什么?
2.正弦定理的内容是什么?
二、新知探究
已知两角及一边解三角形
:在△ABC中,已知c=10,A=45°,C=30°,解这个三角形.
【解】因为A=45°,C=30°,所以B=180°-(A+C)=105°.
由=得a==10×=10.
因为sin 75°=sin(30°+45°)=sin 30°cos 45°+cos 30°sin 45°=,所以b===20×=5+5.
已知三角形的两角和任一边解三角形的思路
(1)若所给边是已知角的对边时,可由正弦定理求另一角所对的边,再由三角形内角和定理求出第三个角.
(2)若所给边不是已知角的对边时,先由三角形内角和定理求出第三个角,再由正弦定理求另外两边.
已知两边及其中一边的对角解三角形
已知△ABC中的下列条件,解三角形:
(1)a=10,b=20,A=60°;
(2)a=2,c=,C=.
解:(1)因为=,
所以sin B===>1,
所以三角形无解.
(2)因为=,所以sin A==.
因为c>a,所以C>A.所以A=.
所以B=,b= ==+1.
互动探究:
变条件:若本例(2)中C=改为A=,其他条件不变,求C,B, b.
解:因为=,所以sin C==.
所以C=或.
当C=时,B=,b==+1.
当C=时,B=,b==-1.
(1)已知两边及其中一边的对角解三角形的思路
①首先由正弦定理求出另一边对角的正弦值;
②如果已知的角为大边所对的角时,由三角形中大边对大角,大角对大边的法则能判断另一边所对的角为锐角,由正弦值可求锐角;
③如果已知的角为小边所对的角时,则不能判断另一边所对的角为锐角,这时由正弦值可求两个角,要分类讨论.
(2)已知两边及其中一边的对角判断三角形解的个数的方法
①应用三角形中大边对大角的性质以及正弦函数的值域判断解的个数;
②在△ABC中,已知a,b和A,以点C为圆心,以边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形解的个数,解的个数见下表:
A为钝角 A为直角 A为锐角
a>b 一解 一解 一解
a=b 无解 无解 一解
absin A 两解
a=bsin A 一解
a
:已知在△ABC中,角A,B所对的边分别是a和b,若acos B=bcos A,则△ABC一定是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
解析:由正弦定理得:acos B=bcos A sin Acos B=sin Bcos A sin(A-B)=0,由于-π<A-B<π,故必有A-B=0,A=B,即△ABC为等腰三角形.
答案:A
互动探究:
变条件:若把本例条件变为“bsin B=csin C”,试判断△ABC的形状.
解:由bsin B=csin C可得sin2B=sin2C,因为三角形内角和为180°,
所以sin B=sin C.所以B=C.故△ABC为等腰三角形.
判断三角形形状的两种途径
注意:在两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.
三、课堂总结
1.正弦定理
条件 在△ABC中,角A,B,C所对的边分别为a,b,c
结论 ==
文字 叙述 在一个三角形中,各边和它所对角的正弦的比相等
■名师点拨
对正弦定理的理解
(1)适用范围:正弦定理对任意的三角形都成立.
(2)结构形式:分子为三角形的边长,分母为相应边所对角的正弦的连等式.
(3)揭示规律:正弦定理指出的是三角形中三条边与其对应角的正弦之间的一个关系式,它描述了三角形中边与角的一种数量关系.
2.正弦定理的变形
若R为△ABC外接圆的半径,则
(1)a=2Rsin A,b=2Rsin B,c=2Rsin C;
(2)sin A=,sin B=,sin C=;
(3)sin A∶sin B∶sin C=a∶b∶c;
(4)=2R.
四、课堂检测
1.(2019·辽宁沈阳铁路实验中学期中考试)在△ABC中,AB=2,AC=3,B=60°,则cos C=( )
A. B.
C. D.
解析:选B.由正弦定理,得=,即=,解得sin C=.因为AB<AC,所以C<B,所以cos C==.
2.在△ABC中,角A,B,C的对边分别为a,b,c,且A∶B∶C=1∶2∶3,则a∶b∶c=( )
A.1∶2∶3 B.3∶2∶1
C.2∶∶1 D.1∶∶2
解析:选D.在△ABC中,因为A∶B∶C=1∶2∶3,所以B=2A,C=3A,又A+B+C=180°,所以A=30°,B=60°,C=90°,所以a∶b∶c=sin A∶sin B∶sin C=sin 30°∶sin 60°∶sin 90°=1∶∶2.
3.在△ABC中,角A,B,C的对边分别是a,b,c,若c-acos B=(2a-b)cos A,则△ABC的形状是( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
解析:选D.已知c-acos B=(2a-b)cos A,由正弦定理得sin C-sin Acos B=2sin Acos A-sin Bcos A,所以sin(A+B)-sin Acos B=2sin Acos A-sin Bcos A,化简得cos A(sin B-sin A)=0,所以cos A=0或sin B-sin A=0,则A=90°或A=B,故△ABC为等腰三角形或直角三角形.
【第四课时】
教学重难点 教学目标 核心素养
测量中的术语 理解测量中的基线等有关名词、术语的确切含义 直观想象
测量距离、高度、角度问题 会利用正、余弦定理解决生产实践中的有关距离、高度、角度等问题 数学建模
【教学过程】
一、问题导入
预习教材内容,思考以下问题:
1.什么是基线?
2.基线的长度与测量的精确度有什么关系?
3.利用正、余弦定理可解决哪些实际问题?
二、新知探究
测量距离问题
:海上A,B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B岛与C岛间的距离是________.
解析:如图,在△ABC中,∠C=180°-(∠B+∠A)=45°,
由正弦定理,可得=,
所以BC=×10=5(海里).
答案:5海里
变条件:在本例中,若“从B岛望C岛和A岛成75°的视角”改为“A,C两岛相距20海里”,其他条件不变,又如何求B岛与C岛间的距离呢?
解:由已知在△ABC中,AB=10,AC=20,∠BAC=60°,即已知两边和两边的夹角,利用余弦定理求解即可.
BC2=AB2+AC2-2AB·AC·cos 60°=102+202-2×10×20×=300.故BC=10.
即B,C间的距离为10海里.
测量距离问题的解题思路
求解测量距离问题的方法是:选择合适的辅助测量点,构造三角形,将问题转化为求某个三角形的边长问题,从而利用正、余弦定理求解.构造数学模型时,尽量把已知元素放在同一个三角形中.
测量高度问题
:如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=________m.
解析:由题意,在△ABC中,∠BAC=30°,∠ABC=180°-75°=105°,故∠ACB=45°.
又AB=600 m,故由正弦定理得=,
解得BC=300 m.在Rt△BCD中,CD=BC·tan 30°=300×=100(m).
答案:100
互动探究:
变问法:在本例条件下,汽车在沿直线AB方向行驶的过程中,若测得观察山顶D点的最大仰角为α,求tan α的值.
解:如图,过点C,作CE⊥AB,垂足为E,则∠DEC=α,由例题可知,
∠CBE=75°,BC=300,
所以CE=BC·sin∠CBE
=300sin 75°
=300×
=150+150.
所以tan α===.
测量高度问题的解题思路
高度的测量主要是一些底部不能到达或者无法直接测量的物体的高度问题.常用正弦定理或余弦定理计算出物体的顶部或底部到一个可到达的点之间的距离,然后转化为解直角三角形的问题.这类物体高度的测量是在与地面垂直的竖直平面内构造三角形或者在空间构造三棱锥,再依据条件利用正、余弦定理解其中的一个或者几个三角形,从而求出所需测量物体的高度.
测量角度问题
:岛A观察站发现在其东南方向有一艘可疑船只,正以每小时10海里的速度向东南方向航行(如图所示),观察站即刻通知在岛A正南方向B处巡航的海监船前往检查.接到通知后,海监船测得可疑船只在其北偏东75°方向且相距10海里的C处,随即以每小时10海里的速度前往拦截.
(1)问:海监船接到通知时,在距离岛A多少海里处?
(2)假设海监船在D处恰好追上可疑船只,求它的航行方向及其航行的时间.
解:(1)根据题意得∠BAC=45°,∠ABC=75°,BC=10,
所以∠ACB=180°-75°-45°=60°,
在△ABC中,由=,
得AB====5.
所以海监船接到通知时,在距离岛A 5 海里处.
(2)设海监船航行时间为t小时,则BD=10t,CD=10t,
又因为∠BCD=180°-∠ACB=180°-60°=120°,
所以BD2=BC2+CD2-2BC·CDcos 120°,
所以300t2=100+100t2-2×10×10t·,
所以2t2-t-1=0,
解得t=1或t=-(舍去).
所以CD=10,所以BC=CD,
所以∠CBD=(180°-120°)=30°,
所以∠ABD=75°+30°=105°.
所以海监船沿方位角105°航行,航行时间为1个小时.
(或海监船沿南偏东75°方向航行,航行时间为1个小时)
测量角度问题的基本思路
(1)测量角度问题的关键是在弄清题意的基础上,画出表示实际问题的图形,在图形中标出相关的角和距离.
(2)根据实际选择正弦定理或余弦定理解三角形,然后将解得的结果转化为实际问题的解.
三、课堂总结
1.基线
在测量过程中,我们把根据测量的需要而确定的线段叫做基线
实际测量中的有关名称、术语
名称 定义 图示
仰角 在同一铅垂平面内,视线在水平线上方时与水平线的夹角
俯角 在同一铅垂平面内,视线在水平线下方时与水平线的夹角
方向角 从指定方向线到目标方向线的水平角(指定方向线是指正北或正南或正东或正西,方向角小于90°) 南偏西60°(指以正南方向为始边,转向目标方向线形成的角)
方位角 从正北的方向线按顺时针到目标方向线所转过的水平角
四、课堂检测
1.若P在Q的北偏东44°50′方向上,则Q在P的( )
A.东偏北45°10′方向上 B.东偏北45°50′方向上
C.南偏西44°50′方向上 D.西偏南45°50′方向上
解析:选C.如图所示.
2.如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=200米,点C位于BD上,则山高AB等于( )
A.100米 B.50(+1)米
C.100(+1)米 D.200米
解析:选C.设AB=x米,在Rt△ACB中,∠ACB=45°,
所以BC=AB=x.
在Rt△ABD中,∠D=30°,则BD=AB=x.
因为BD-BC=CD,所以x-x=200,
解得x=100(+1).故选C.
3.已知台风中心位于城市A东偏北α(α为锐角)度的150公里处,以v公里/小时沿正西方向快速移动,2.5小时后到达距城市A西偏北β(β为锐角)度的200公里处,若cos α=cos β,则v=( )
A.60 B.80
C.100 D.125
解析:选C.画出图象如图所示,由余弦定理得(2.5v)2=2002+1502+2×200×150cos(α+β)①,由正弦定理得=,所以sin α=sin β.又cos α= cos β,sin2 α+cos2 α=1,解得sin β=,故cos β=,sin α=,cos α=,故cos(α+β)=-=0,代入①解得v=100.
4.某巡逻艇在A处发现在北偏东45°距A处8海里处有一走私船,正沿南偏东75°的方向以12海里/小时的速度向我岸行驶,巡逻艇立即以12海里/小时的速度沿直线追击,问巡逻艇最少需要多长时间才能追到走私船,并指出巡逻艇的航行方向.
解:设经过t小时在点C处刚好追上走私船,依题意:AC=12t,BC=12t,∠ABC=120°,
在△ABC中,由正弦定理得=,
所以sin∠BAC=,所以∠BAC=30°,
所以AB=BC=8=12t,解得t=,航行的方向为北偏东75°.
即巡逻艇最少经过小时可追到走私船,沿北偏东75°的方向航行.
1 / 18
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
