人教版数学九年级上册《扇形面积和弧长复习》课件(16张ppt)
文档属性
| 名称 | 人教版数学九年级上册《扇形面积和弧长复习》课件(16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 557.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 19:18:38 | ||
图片预览





文档简介
(共16张PPT)
扇形面积和弧长(复习课)
1、半径为R的圆周长:
3、半径为R的圆面积:
2、半径为R,n°的圆心角所对的弧长为:
4、半径为R,n°的圆心角所对的扇形面积为
知识框架
n°
A
B
O
R
l
5、半径为R,弧长为 l 的扇形
面积为
1、求扇形面积
2、求阴影部分的面积
求扇形面积
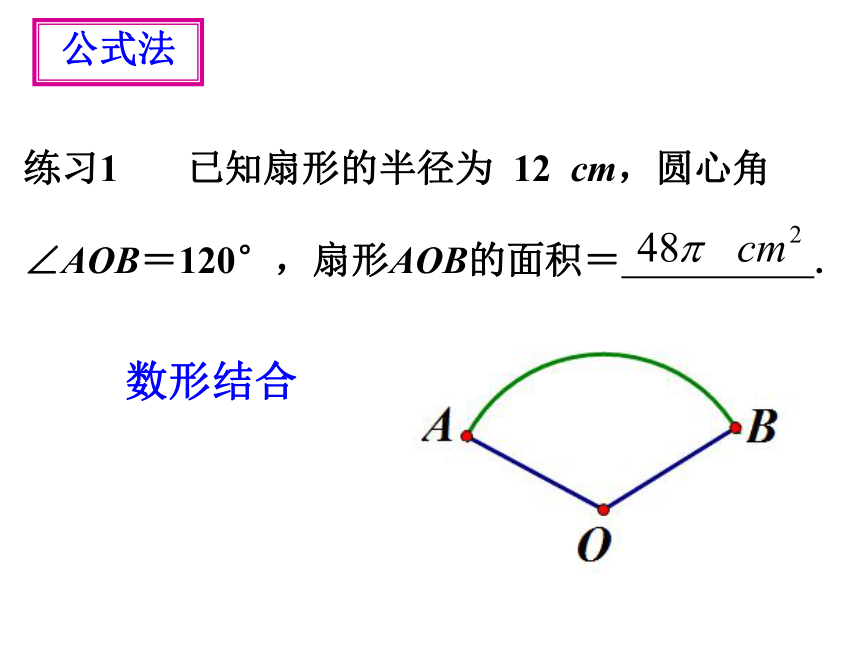
练习1 已知扇形的半径为 12 cm,圆心角
∠AOB=120°,扇形AOB的面积= .
公式法
数形结合
求阴影部分的面积
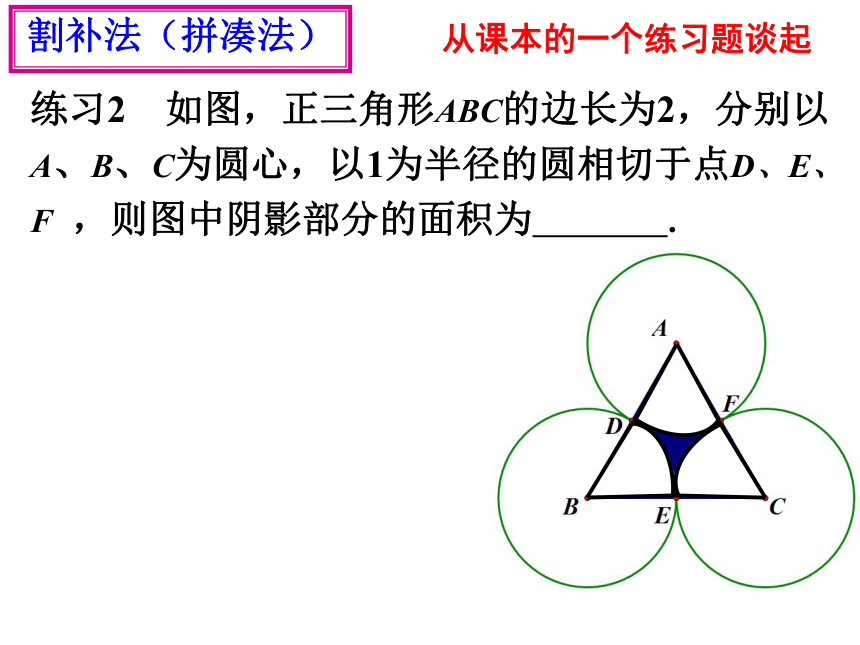
练习2 如图,正三角形ABC的边长为2,分别以A、B、C为圆心,以1为半径的圆相切于点D、E、F ,则图中阴影部分的面积为 .
割补法(拼凑法)
从课本的一个练习题谈起
练习2 如图,正三角形ABC的边长为2,分别以A、B、C为圆心,以1为半径的圆相切于点D、E、F ,则图中阴影部分的面积为 .
割补法(拼凑法)
从课本的一个练习题谈起
解:
根据勾股定理,可求得
则AE⊥BC,
在Rt△ABE中,
连接AE,
2
60°
60°
60°
1
1
2
2
思考:本题中求扇形面积时还有其他解法吗?
变式1 如图,以△ABC的顶点为圆心的⊙A、⊙B、⊙C 两两不相交,且半径都是0.5 cm,则图中三个扇形(即阴影部分)的面积之和是 .
A
C
B
割补法(拼凑法)
变式2 如图,以四边形ABCD的顶点为圆心的⊙A、⊙B、⊙C、⊙D两两不相交,且半径都是2 cm,则图中阴影部分的面积是 .
割补法(拼凑法)
练习 如图方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为 。
割补法(拼凑法)
练习3 如图,C是半径为1的⊙O上一点,A是⊙O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于 .
等积法
练习3 如图,C是半径为1的⊙O上一点,A是⊙O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于 .
等积法
2
1
1
30°
60°
60°
60°
转化?
问:从左边到右边转化成立的关键是什么?
变式 半圆的直径AB=10, P是AB上任意一点,点C、D 是半圆的三等分点,则图中阴影部分面积等于 .
等积法
知识小结
这节课我们都复习了什么?
求阴影部分的面积的方法有哪些?
学案上的题
作业布置
扇形面积和弧长(复习课)
1、半径为R的圆周长:
3、半径为R的圆面积:
2、半径为R,n°的圆心角所对的弧长为:
4、半径为R,n°的圆心角所对的扇形面积为
知识框架
n°
A
B
O
R
l
5、半径为R,弧长为 l 的扇形
面积为
1、求扇形面积
2、求阴影部分的面积
求扇形面积
练习1 已知扇形的半径为 12 cm,圆心角
∠AOB=120°,扇形AOB的面积= .
公式法
数形结合
求阴影部分的面积
练习2 如图,正三角形ABC的边长为2,分别以A、B、C为圆心,以1为半径的圆相切于点D、E、F ,则图中阴影部分的面积为 .
割补法(拼凑法)
从课本的一个练习题谈起
练习2 如图,正三角形ABC的边长为2,分别以A、B、C为圆心,以1为半径的圆相切于点D、E、F ,则图中阴影部分的面积为 .
割补法(拼凑法)
从课本的一个练习题谈起
解:
根据勾股定理,可求得
则AE⊥BC,
在Rt△ABE中,
连接AE,
2
60°
60°
60°
1
1
2
2
思考:本题中求扇形面积时还有其他解法吗?
变式1 如图,以△ABC的顶点为圆心的⊙A、⊙B、⊙C 两两不相交,且半径都是0.5 cm,则图中三个扇形(即阴影部分)的面积之和是 .
A
C
B
割补法(拼凑法)
变式2 如图,以四边形ABCD的顶点为圆心的⊙A、⊙B、⊙C、⊙D两两不相交,且半径都是2 cm,则图中阴影部分的面积是 .
割补法(拼凑法)
练习 如图方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为 。
割补法(拼凑法)
练习3 如图,C是半径为1的⊙O上一点,A是⊙O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于 .
等积法
练习3 如图,C是半径为1的⊙O上一点,A是⊙O外一点,且OA=2,AB是⊙O的切线,BC//OA,连结AC,则阴影部分面积等于 .
等积法
2
1
1
30°
60°
60°
60°
转化?
问:从左边到右边转化成立的关键是什么?
变式 半圆的直径AB=10, P是AB上任意一点,点C、D 是半圆的三等分点,则图中阴影部分面积等于 .
等积法
知识小结
这节课我们都复习了什么?
求阴影部分的面积的方法有哪些?
学案上的题
作业布置
同课章节目录
