人教版数学九年级上册22.3实际问题与二次函数——利润问题课件(52张ppt)
文档属性
| 名称 | 人教版数学九年级上册22.3实际问题与二次函数——利润问题课件(52张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 00:00:00 | ||
图片预览









文档简介
(共52张PPT)
22.3 实际问题与二次函数
之利润问题
1.掌握商品经济等问题中的相等关系的寻找方法,并会应用函数关系式求利润的最值;
2.会应用二次函数的性质解决实际问题.
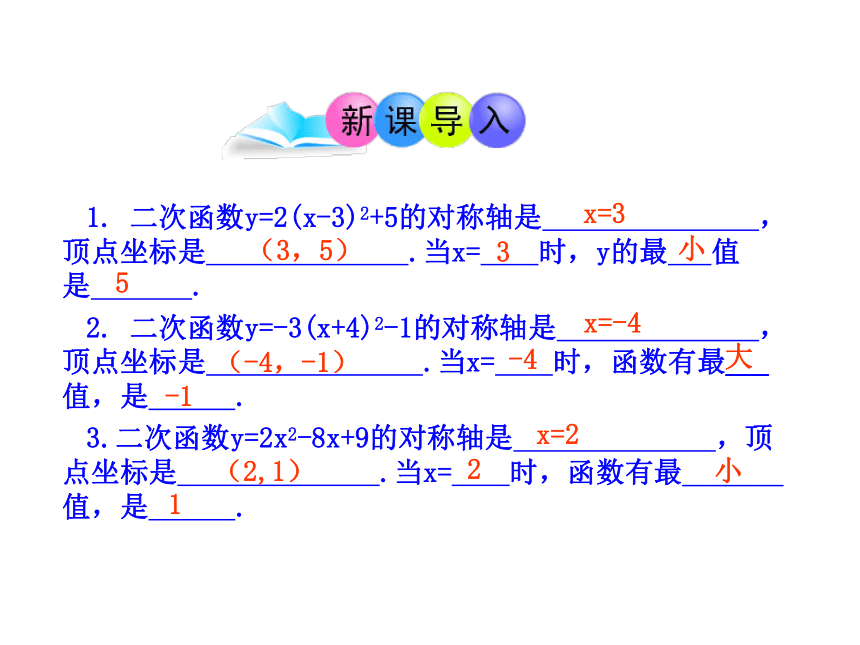
1. 二次函数y=2(x-3)2+5的对称轴是 ,顶点坐标是 .当x= 时,y的最 值是 .
2. 二次函数y=-3(x+4)2-1的对称轴是 ,顶点坐标是 .当x= 时,函数有最___ 值,是 .
3.二次函数y=2x2-8x+9的对称轴是 ,顶点坐标是 .当x= 时,函数有最_______ 值,是 .
x=3
(3,5)
3
小
5
x=-4
(-4,-1)
-4
大
-1
x=2
(2,1)
2
1
小
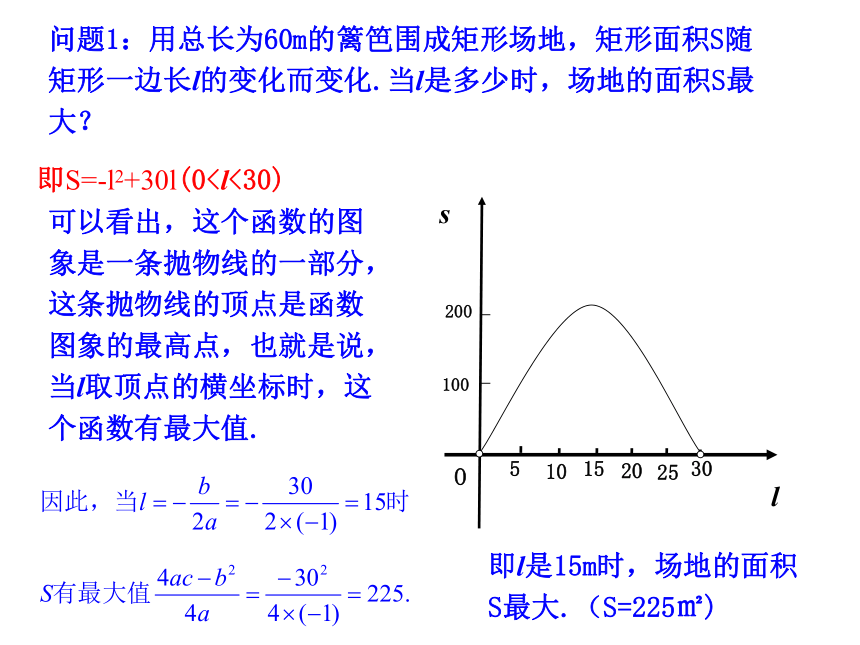
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l的值.
矩形场地的周长是60m,一边长为l,则另一边长为
m,场地的面积: (0S=l(30-l)
即S=-l2+30l
请同学们画出此函数的图象
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说,当l取顶点的横坐标时,这个函数有最大值.
5
10
15
20
25
30
100
200
l
s
即l是15m时,场地的面积S最大.(S=225㎡)
O
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
即S=-l2+30l(0一般地,因为抛物线y=ax2+bx+c的顶点是最低(高)点,所以当 时,二次函数y=ax2+bx+c有最小(大)值 .
问题2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
请同学们带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品
的利润y也随之变化,我们先来确定y与x的函数关系式.涨
价x元,则每星期少卖 件,实际卖出 件,
每件利润为 元,因此,所得利润
为 元.
10x
(300-10x)
(60+x-40)
(60+x-40)(300-10x)
y=(60+x-40)(300-10x)
(0≤x≤30)
即y=-10(x-5)2+6250
∴当x=5时,y最大值=6250
怎样确定x的取值范围
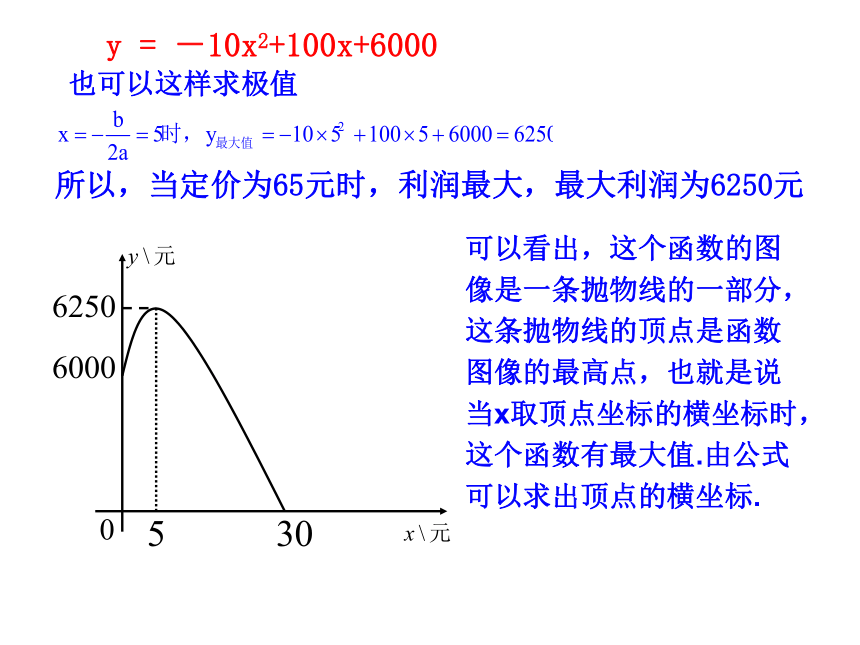
= -10x2+100x+6000
可以看出,这个函数的图像是一条抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值.由公式可以求出顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元
也可以这样求极值
y = -10x2+100x+6000
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案.
解析:设降价x元时利润最大,则每星期可多卖20x件,实际卖出(300+20x)件,每件利润为(60-40-x)元,因此,得利润
y=(300+20x)(60-40-x)
=-20(x -5x+6.25)+6125
=-20x2+100x+6000
=-20(x-2.5) +6125
∴x=2.5时,y极大值=6125
你能回答了吧!
怎样确定x的取值范围
(0≤x≤20)
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值.
解决这类题目的一般步骤
1.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是 cm2.
2.某商店购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,据销售经验,售价每提高1元,销售量相应减少10个. (1)假设销售单价提高x元,那么销售每个篮球所获得的利润是_______元,这种篮球每月的销售量是 个(用x的代数式表示)
(2)8000元是否为每月销售篮球的最大利润
如果是,说明理由,如果不是,请求出最大月利润,
此时篮球的售价应定为多少元
x+10
500 10x
8000元不是每月最大利润,最大月利润为9000元,此时篮球的售价为70元.
y=-10x2+400x+5000 (0≤x≤50)
1.主要学习了如何将实际问题转化为数学问题,特别是如何利用二次函数的有关性质解决实际问题的方法.
2.利用二次函数解决实际问题时,根据利润公式等关系写出二次函数表达式是解决问题的关键.
3.某商店经营一种小商品,进价为2.5元,据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售单价每降低1元,平均每天就可以多售出100件.
(1)假设每件商品降低x元,商店每天销售这种小商品的利润是y元,请你写出y与x之间的函数关系式,并注明x的取值范围;
(2)每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?(注:销售利润=销售收入-购进成本)
解析:(1)降低x元后,所销售的件数是(500+100x),
y=-100x2+600x+5500 (0<x≤11 )
(2)y=-100x2+600x+5500 (0<x≤11 )
配方得y=-100(x-3)2+6400
当x=3时,y的最大值是6400元.
即降价为3元时,利润最大.
所以销售单价为10.5元时,最大利润为6400元.
答:销售单价为10.5元时,最大利润为6400元.
4.我市一家电子计算器专卖店每只进价13元,售价20元,多买优惠 ;凡是一次买10只以上的,每多买1只,所买的全部计算器每只就降低0.10元,例如, 某人买20只计算器,于是每只降价0.10×(20-10)=1(元),因此,所买的全部20只计算器都按照每只19元计算,但是最低价为每只16元.
(1).求一次至少买多少只,才能以最低价购买?
(2).写出该专卖店当一次销售x(只)时,所获利润y(元)与x之间的函数关系式,并写出自变量x的取值范围;
(3)若店主一次卖的只数在10至50只之间,问一次卖多少只获得的利润最大?其最大利润为多少?
【解析】(1)设一次购买x只,才能以最低价购买,则有:
0.1(x-10)=20-16,解这个方程得x=50.
答:一次至少买50只,才能以最低价购买
(2)
(说明:因三段图象首尾相连,所以端点10、50包括在哪个区间均可)
(3)将 配方得 ,所以店主一次卖
40只时可获得最高利润,最高利润为160元.(也可用公式
法求得)
5.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)在此期间该养殖场每天的捕捞量与前一末的捕捞量相比是如何变化的?
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且
能在当天全部售出,求第x天的收入y(元)与x(天)之
间的函数关系式?(当天收入=日销售额-日捕捞成本) 试说明(2)中的函数y随x的变化情况,并指出在第几天
y取得最大值,最大值是多少?
解:(1)该养殖场每天的捕捞量与前一天相比减少10kg; (2)由题意,得
(3)∵-2<0,y=-2x2+40x+14250=-2(x-10)2+14450, 又∵1≤x≤20且x为整数, ∴当1≤x≤10时,y随x的增大而增大; 当10≤x≤20时,y随x的增大而减小; 当x=10时即在第10天,y取得最大值,最大值为14450.
九年级 上册
22.3 实际问题与二次函数 (第1课时)
本节课是在学生学习完二次函数的图象和性质的知识 的基础上的进一步拓展与应用.
课件说明
学习目标: 能够表示实际问题中变量之间的二次函数关系,会运 用二次函数的顶点坐标求出实际问题的最大值(或最 小值).
学习重点: 探究利用二次函数的最大值(或最小值)解决实际问 题的方法.
课件说明
从地面竖直向上抛出一小球,小球的高度 h(单位: m)与小球的运动时间 t(单位:s)之间的关系式是 h= 30t - 5t 2 (0≤t≤6).小球的运动时间是多少时,小 球最高?小球运动中的最大高度是多少?
1.创设情境,引出问题
小球运动的时间是 3 s 时,小球最高.
小球运动中的最大高度是 45 m.
2.结合问题,拓展一般
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点, 当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
3.类比引入,探究问题
整理后得
用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化.当 l 是多少米时,场地 的面积 S 最大?
解: ,
∴ 当 时,
S 有最大值为 .
当 l 是 15 m 时,场地的面积 S 最大.
(0<l<30).
( )
( )
4.归纳探究,总结方法
2.列出二次函数的解析式,并根据自变量的实际 意义,确定自变量的取值范围.
3.在自变量的取值范围内,求出二次函数的最大 值或最小值.
1.由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
5.运用新知,拓展训练
为了改善小区环境,某小区决定要在一块一边靠墙 (墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿 化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如 下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y m 2.
(1)求 y 与 x 之间的函数关系 式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件 的绿化带的面积最大?
D
C
B
A
25 m
(1) 如何求二次函数的最小(大)值,并利用其 解决实际问题?
(2) 在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
6.课堂小结
教科书习题 22.3 第 1,4,5 题.
7.布置作业
九年级 上册
22.3 实际问题与二次函数 (第2课时)
二次函数是单变量最优化问题的数学模型,如生活中 涉及的求最大利润,最大面积等.这体现了数学的实 用性,是理论与实践结合的集中体现.本节课主要来 研究利润问题.
课件说明
学习目标: 能够分析和表示实际问题中,变量之间的二次函数关 系,并运用二次函数的顶点坐标求出实际问题的最大 (小)值.
学习重点: 探究利用二次函数的最大值(或最小值)解决实际问 题的方法.
课件说明
问题1
解决上节课所讲的实际问题时,你用到了什么知识? 所用知识在解决生活中问题时,还应注意哪些问题?
1.复习二次函数解决实际问题的方法
1.复习二次函数解决实际问题的方法
2.列出二次函数的解析式,并根据自变量的实际 意义,确定自变量的取值范围;
3.在自变量的取值范围内,求出二次函数的最大 值或最小值.
归纳: 1.由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
问题2
某商品现在的售价为每件 60 元,每星期可卖出300件.市场调查反映:如调整价格,每涨价 1 元,每星期要少卖出 10 件;每降价 1 元,每星期可多卖出 20 件. 已知商品的进价为每件 40 元,如何定价才能使利润最大?
2.探究二次函数利润问题
(1) 题目中有几种调整价格的方法?
(2) 题目涉及哪些变量?哪一个量是自变量?哪 些量随之发生了变化?哪个量是函数?
(3) 当每件涨 1 元时,售价是多少?每星期销量是多少?成本是多少?销售额是多少?利润呢?
(4) 最多能涨多少钱呢?
(5) 当每件涨 x 元时,售价是多少?每星期销量是多少?成本是多少?销售额是多少?利润 y 呢?
2.探究二次函数利润问题
300-10x 60+x -40 300-10x
( )
( )
( )
y=
(6)这是一个什么函数?自变量取值范围是什么? 这个函数有最大值吗?
2.探究二次函数利润问题
(0≤x≤30).
问题3
x = 5 是在自变量取值范围内吗?为什么?
如果计算出的 x 不在自变量取值范围内,怎么办?
2.探究二次函数利润问题
(1) x = 2.5 是在自变量取值范围内吗?
(2)由上面的讨论及现在的销售情况, 你知道应 如何定价能使利润最大了吗?
问题4
在降价情况下,最大利润是多少?请你参考上述的讨论,自己得出答案.
2.探究二次函数利润问题
(1)这节课学习了用什么知识解决哪类问题? (2)解决问题的一般步骤是什么?应注意哪些问 题? (3)你学到了哪些思考问题的方法?
3.小结
教科书习题 22.3 第 2,8 题.
4.课后反思,布置作业
22.3 实际问题与二次函数
(第1课时)
探究
构建二次函数模型解决 一些实际问题
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如果调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
分析:调整价格包括涨价和降价两种情况,我们先来看涨价的情况.
即
y = (60+x)(300-10x) -40 (300-10x)
(1)设每件涨价x元,则每星期售出商品的利润y随之变化.我们先来确定y随x变化的函数式.涨价x元时,每星期少卖10x件,实际卖出(300-10x)件,销售额为( 60+x )( 300-10x ),买进商品需付出40 ( 300-10x )
y = -10x2+100x+6000
怎样确定x的取值范围?
其中,0≤x≤30.
根据上面的函数,填空:
当x = ________时,y最大,也就是说,在涨价的情况下,涨价_____元,
即定价_________元时,利润最大,最大利润是___________.
y = -10x2+100x+6000
5
5
65
6250
其中,0≤x≤30.
(2)在降价的情况下,最大利润是多少?请你参考(1)的讨论自己得出答案.
分析:我们来看降价的情况.
(2)设每件降价x元,则每星期售出商品的利润y随之变化.我们先来确定y随x变化的函数式.降价x元时,每星期多卖18x件,实际卖出(300+18x)件,销售额为( 60-x )( 300+18x ),买进商品需付出40 ( 300+18x ),因此所得的利润
y = ( 60-x )( 300+18x ) - 40 ( 300+18x )
即
y = -18x2+60x+6000
当
由(1)(2)的讨论及现在的想做状况,你知道应如何定价能使利润最大了吗?
构建二次函数模型:将问题转化为二次函数的一个具体的表达式.
求二次函数的最大(或最小值):求这个函数的最大(或最小值)
运用函数来决策定价的问题:
某商场第一年销售计算机5000台,如果每年的销售量比上一年增加的百分率相同的百分率为x,写出第三年的销售量增加百分比的函数关系式
解:依题意
y = 5000 (1+x ) 2
做 一 做
某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(200-x)件,应该如何定价才能使利润最大?
某商店经营T恤衫,已知成批购进时单价是2.5元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件.
请你帮助分析,销售单价是多少时,可以获利最多?
设销售单价为 x( x ≤13.5)元,那么
(1)销售量可以表示为__________________;
(2)销售额可以表示为____________________;
(3)所获利润可以表示为____________________;
(4)当销售单价是_____________元时,可以获得最大利润,最大利润是___________________.
3200-200x
3200x-200x2
-200x2+3700x-8000
9.25元
9112.5元
某商店购进一批单价为20元的日用商品,如果以单价30元销售那么半月内可售出400件,根据销售经验,推广销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.如何提高售价,才能在半月内获得最大利润?
1. 当销售单价提高5元,即销售单价为35元时,可以获得最大利润4500元.提示:设销售单价为x(x≥30)元,销售利润为y元,则
y = ( x-20 )[400-20(x-30)]=-20x2+140x-20000
22.3 实际问题与二次函数
之利润问题
1.掌握商品经济等问题中的相等关系的寻找方法,并会应用函数关系式求利润的最值;
2.会应用二次函数的性质解决实际问题.
1. 二次函数y=2(x-3)2+5的对称轴是 ,顶点坐标是 .当x= 时,y的最 值是 .
2. 二次函数y=-3(x+4)2-1的对称轴是 ,顶点坐标是 .当x= 时,函数有最___ 值,是 .
3.二次函数y=2x2-8x+9的对称轴是 ,顶点坐标是 .当x= 时,函数有最_______ 值,是 .
x=3
(3,5)
3
小
5
x=-4
(-4,-1)
-4
大
-1
x=2
(2,1)
2
1
小
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l的值.
矩形场地的周长是60m,一边长为l,则另一边长为
m,场地的面积: (0
即S=-l2+30l
请同学们画出此函数的图象
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说,当l取顶点的横坐标时,这个函数有最大值.
5
10
15
20
25
30
100
200
l
s
即l是15m时,场地的面积S最大.(S=225㎡)
O
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
即S=-l2+30l(0
问题2:某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:如调整价格,每涨价1元,每星期少卖出10件;每降价1元,每星期可多卖出20件,已知商品的进价为每件40元,如何定价才能使利润最大?
请同学们带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品
的利润y也随之变化,我们先来确定y与x的函数关系式.涨
价x元,则每星期少卖 件,实际卖出 件,
每件利润为 元,因此,所得利润
为 元.
10x
(300-10x)
(60+x-40)
(60+x-40)(300-10x)
y=(60+x-40)(300-10x)
(0≤x≤30)
即y=-10(x-5)2+6250
∴当x=5时,y最大值=6250
怎样确定x的取值范围
= -10x2+100x+6000
可以看出,这个函数的图像是一条抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值.由公式可以求出顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元
也可以这样求极值
y = -10x2+100x+6000
在降价的情况下,最大利润是多少?请你参考(1)的过程得出答案.
解析:设降价x元时利润最大,则每星期可多卖20x件,实际卖出(300+20x)件,每件利润为(60-40-x)元,因此,得利润
y=(300+20x)(60-40-x)
=-20(x -5x+6.25)+6125
=-20x2+100x+6000
=-20(x-2.5) +6125
∴x=2.5时,y极大值=6125
你能回答了吧!
怎样确定x的取值范围
(0≤x≤20)
由(1)(2)的讨论及现在的销售情况,你知道应该如何定价能使利润最大了吗
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值.
解决这类题目的一般步骤
1.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是 cm2.
2.某商店购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,据销售经验,售价每提高1元,销售量相应减少10个. (1)假设销售单价提高x元,那么销售每个篮球所获得的利润是_______元,这种篮球每月的销售量是 个(用x的代数式表示)
(2)8000元是否为每月销售篮球的最大利润
如果是,说明理由,如果不是,请求出最大月利润,
此时篮球的售价应定为多少元
x+10
500 10x
8000元不是每月最大利润,最大月利润为9000元,此时篮球的售价为70元.
y=-10x2+400x+5000 (0≤x≤50)
1.主要学习了如何将实际问题转化为数学问题,特别是如何利用二次函数的有关性质解决实际问题的方法.
2.利用二次函数解决实际问题时,根据利润公式等关系写出二次函数表达式是解决问题的关键.
3.某商店经营一种小商品,进价为2.5元,据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售单价每降低1元,平均每天就可以多售出100件.
(1)假设每件商品降低x元,商店每天销售这种小商品的利润是y元,请你写出y与x之间的函数关系式,并注明x的取值范围;
(2)每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?(注:销售利润=销售收入-购进成本)
解析:(1)降低x元后,所销售的件数是(500+100x),
y=-100x2+600x+5500 (0<x≤11 )
(2)y=-100x2+600x+5500 (0<x≤11 )
配方得y=-100(x-3)2+6400
当x=3时,y的最大值是6400元.
即降价为3元时,利润最大.
所以销售单价为10.5元时,最大利润为6400元.
答:销售单价为10.5元时,最大利润为6400元.
4.我市一家电子计算器专卖店每只进价13元,售价20元,多买优惠 ;凡是一次买10只以上的,每多买1只,所买的全部计算器每只就降低0.10元,例如, 某人买20只计算器,于是每只降价0.10×(20-10)=1(元),因此,所买的全部20只计算器都按照每只19元计算,但是最低价为每只16元.
(1).求一次至少买多少只,才能以最低价购买?
(2).写出该专卖店当一次销售x(只)时,所获利润y(元)与x之间的函数关系式,并写出自变量x的取值范围;
(3)若店主一次卖的只数在10至50只之间,问一次卖多少只获得的利润最大?其最大利润为多少?
【解析】(1)设一次购买x只,才能以最低价购买,则有:
0.1(x-10)=20-16,解这个方程得x=50.
答:一次至少买50只,才能以最低价购买
(2)
(说明:因三段图象首尾相连,所以端点10、50包括在哪个区间均可)
(3)将 配方得 ,所以店主一次卖
40只时可获得最高利润,最高利润为160元.(也可用公式
法求得)
5.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售.九(1)班数学建模兴趣小组根据调查,整理出第x天(1≤x≤20且x为整数)的捕捞与销售的相关信息如表:
(1)在此期间该养殖场每天的捕捞量与前一末的捕捞量相比是如何变化的?
(2)假定该养殖场每天捕捞和销售的鲜鱼没有损失,且
能在当天全部售出,求第x天的收入y(元)与x(天)之
间的函数关系式?(当天收入=日销售额-日捕捞成本) 试说明(2)中的函数y随x的变化情况,并指出在第几天
y取得最大值,最大值是多少?
解:(1)该养殖场每天的捕捞量与前一天相比减少10kg; (2)由题意,得
(3)∵-2<0,y=-2x2+40x+14250=-2(x-10)2+14450, 又∵1≤x≤20且x为整数, ∴当1≤x≤10时,y随x的增大而增大; 当10≤x≤20时,y随x的增大而减小; 当x=10时即在第10天,y取得最大值,最大值为14450.
九年级 上册
22.3 实际问题与二次函数 (第1课时)
本节课是在学生学习完二次函数的图象和性质的知识 的基础上的进一步拓展与应用.
课件说明
学习目标: 能够表示实际问题中变量之间的二次函数关系,会运 用二次函数的顶点坐标求出实际问题的最大值(或最 小值).
学习重点: 探究利用二次函数的最大值(或最小值)解决实际问 题的方法.
课件说明
从地面竖直向上抛出一小球,小球的高度 h(单位: m)与小球的运动时间 t(单位:s)之间的关系式是 h= 30t - 5t 2 (0≤t≤6).小球的运动时间是多少时,小 球最高?小球运动中的最大高度是多少?
1.创设情境,引出问题
小球运动的时间是 3 s 时,小球最高.
小球运动中的最大高度是 45 m.
2.结合问题,拓展一般
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点, 当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
3.类比引入,探究问题
整理后得
用总长为 60 m 的篱笆围成矩形场地,矩形面积 S 随矩形一边长 l 的变化而变化.当 l 是多少米时,场地 的面积 S 最大?
解: ,
∴ 当 时,
S 有最大值为 .
当 l 是 15 m 时,场地的面积 S 最大.
(0<l<30).
( )
( )
4.归纳探究,总结方法
2.列出二次函数的解析式,并根据自变量的实际 意义,确定自变量的取值范围.
3.在自变量的取值范围内,求出二次函数的最大 值或最小值.
1.由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
5.运用新知,拓展训练
为了改善小区环境,某小区决定要在一块一边靠墙 (墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿 化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如 下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y m 2.
(1)求 y 与 x 之间的函数关系 式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件 的绿化带的面积最大?
D
C
B
A
25 m
(1) 如何求二次函数的最小(大)值,并利用其 解决实际问题?
(2) 在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
6.课堂小结
教科书习题 22.3 第 1,4,5 题.
7.布置作业
九年级 上册
22.3 实际问题与二次函数 (第2课时)
二次函数是单变量最优化问题的数学模型,如生活中 涉及的求最大利润,最大面积等.这体现了数学的实 用性,是理论与实践结合的集中体现.本节课主要来 研究利润问题.
课件说明
学习目标: 能够分析和表示实际问题中,变量之间的二次函数关 系,并运用二次函数的顶点坐标求出实际问题的最大 (小)值.
学习重点: 探究利用二次函数的最大值(或最小值)解决实际问 题的方法.
课件说明
问题1
解决上节课所讲的实际问题时,你用到了什么知识? 所用知识在解决生活中问题时,还应注意哪些问题?
1.复习二次函数解决实际问题的方法
1.复习二次函数解决实际问题的方法
2.列出二次函数的解析式,并根据自变量的实际 意义,确定自变量的取值范围;
3.在自变量的取值范围内,求出二次函数的最大 值或最小值.
归纳: 1.由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
问题2
某商品现在的售价为每件 60 元,每星期可卖出300件.市场调查反映:如调整价格,每涨价 1 元,每星期要少卖出 10 件;每降价 1 元,每星期可多卖出 20 件. 已知商品的进价为每件 40 元,如何定价才能使利润最大?
2.探究二次函数利润问题
(1) 题目中有几种调整价格的方法?
(2) 题目涉及哪些变量?哪一个量是自变量?哪 些量随之发生了变化?哪个量是函数?
(3) 当每件涨 1 元时,售价是多少?每星期销量是多少?成本是多少?销售额是多少?利润呢?
(4) 最多能涨多少钱呢?
(5) 当每件涨 x 元时,售价是多少?每星期销量是多少?成本是多少?销售额是多少?利润 y 呢?
2.探究二次函数利润问题
300-10x 60+x -40 300-10x
( )
( )
( )
y=
(6)这是一个什么函数?自变量取值范围是什么? 这个函数有最大值吗?
2.探究二次函数利润问题
(0≤x≤30).
问题3
x = 5 是在自变量取值范围内吗?为什么?
如果计算出的 x 不在自变量取值范围内,怎么办?
2.探究二次函数利润问题
(1) x = 2.5 是在自变量取值范围内吗?
(2)由上面的讨论及现在的销售情况, 你知道应 如何定价能使利润最大了吗?
问题4
在降价情况下,最大利润是多少?请你参考上述的讨论,自己得出答案.
2.探究二次函数利润问题
(1)这节课学习了用什么知识解决哪类问题? (2)解决问题的一般步骤是什么?应注意哪些问 题? (3)你学到了哪些思考问题的方法?
3.小结
教科书习题 22.3 第 2,8 题.
4.课后反思,布置作业
22.3 实际问题与二次函数
(第1课时)
探究
构建二次函数模型解决 一些实际问题
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如果调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大?
分析:调整价格包括涨价和降价两种情况,我们先来看涨价的情况.
即
y = (60+x)(300-10x) -40 (300-10x)
(1)设每件涨价x元,则每星期售出商品的利润y随之变化.我们先来确定y随x变化的函数式.涨价x元时,每星期少卖10x件,实际卖出(300-10x)件,销售额为( 60+x )( 300-10x ),买进商品需付出40 ( 300-10x )
y = -10x2+100x+6000
怎样确定x的取值范围?
其中,0≤x≤30.
根据上面的函数,填空:
当x = ________时,y最大,也就是说,在涨价的情况下,涨价_____元,
即定价_________元时,利润最大,最大利润是___________.
y = -10x2+100x+6000
5
5
65
6250
其中,0≤x≤30.
(2)在降价的情况下,最大利润是多少?请你参考(1)的讨论自己得出答案.
分析:我们来看降价的情况.
(2)设每件降价x元,则每星期售出商品的利润y随之变化.我们先来确定y随x变化的函数式.降价x元时,每星期多卖18x件,实际卖出(300+18x)件,销售额为( 60-x )( 300+18x ),买进商品需付出40 ( 300+18x ),因此所得的利润
y = ( 60-x )( 300+18x ) - 40 ( 300+18x )
即
y = -18x2+60x+6000
当
由(1)(2)的讨论及现在的想做状况,你知道应如何定价能使利润最大了吗?
构建二次函数模型:将问题转化为二次函数的一个具体的表达式.
求二次函数的最大(或最小值):求这个函数的最大(或最小值)
运用函数来决策定价的问题:
某商场第一年销售计算机5000台,如果每年的销售量比上一年增加的百分率相同的百分率为x,写出第三年的销售量增加百分比的函数关系式
解:依题意
y = 5000 (1+x ) 2
做 一 做
某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(200-x)件,应该如何定价才能使利润最大?
某商店经营T恤衫,已知成批购进时单价是2.5元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件.
请你帮助分析,销售单价是多少时,可以获利最多?
设销售单价为 x( x ≤13.5)元,那么
(1)销售量可以表示为__________________;
(2)销售额可以表示为____________________;
(3)所获利润可以表示为____________________;
(4)当销售单价是_____________元时,可以获得最大利润,最大利润是___________________.
3200-200x
3200x-200x2
-200x2+3700x-8000
9.25元
9112.5元
某商店购进一批单价为20元的日用商品,如果以单价30元销售那么半月内可售出400件,根据销售经验,推广销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.如何提高售价,才能在半月内获得最大利润?
1. 当销售单价提高5元,即销售单价为35元时,可以获得最大利润4500元.提示:设销售单价为x(x≥30)元,销售利润为y元,则
y = ( x-20 )[400-20(x-30)]=-20x2+140x-20000
同课章节目录
