人教版数学九年级上册24.1 弧、弦、圆心角课件(23张ppt)
文档属性
| 名称 | 人教版数学九年级上册24.1 弧、弦、圆心角课件(23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
人教版九年级上册
24.1 弧、弦、圆心角
古希腊数学家这样描述圆:
在一切平面图形中,圆是最美的!
1.圆是中心对称图形吗 它的对称中心在哪里
把圆绕圆心旋转任意一个角度后,你发现了什么?
.
动画
圆是中心对称图形,它的对称中心是圆心.
定理:把圆绕圆心旋转任意一个角度后,仍与
原来的圆重合.
创设情境 导入新课
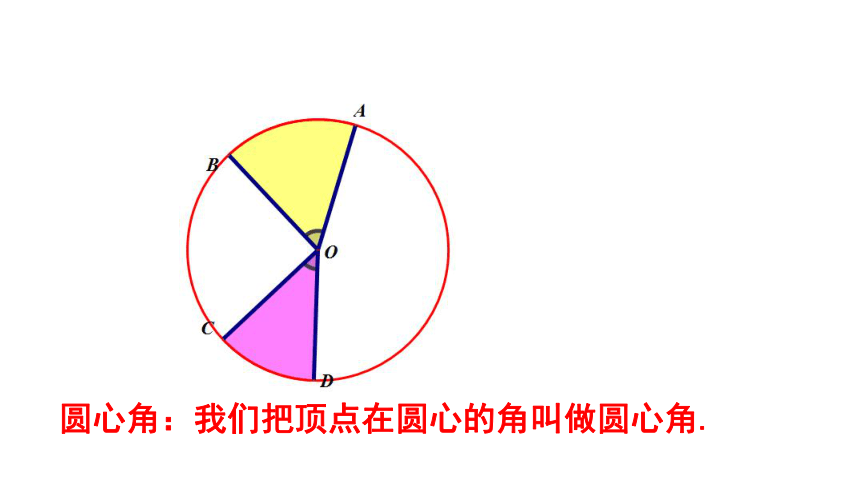
圆心角:我们把顶点在圆心的角叫做圆心角.
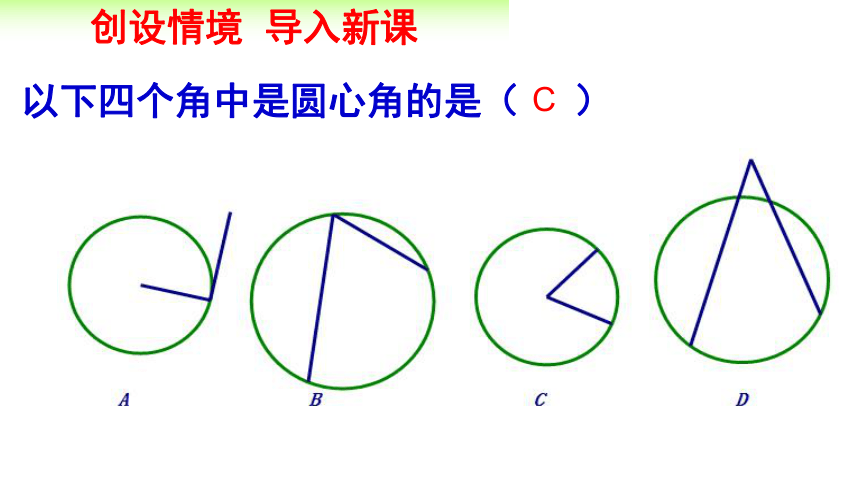
以下四个角中是圆心角的是( )
创设情境 导入新课
C
(1)画两个相等的圆心角,观察它们所对的弧,弦有什么关系?
探究一
合作交流 探究新知
活动要求:①独立画图,在图上标上相应的字母.
②画好图后,小组交流所画的图.
③小组交流所得到的关系.
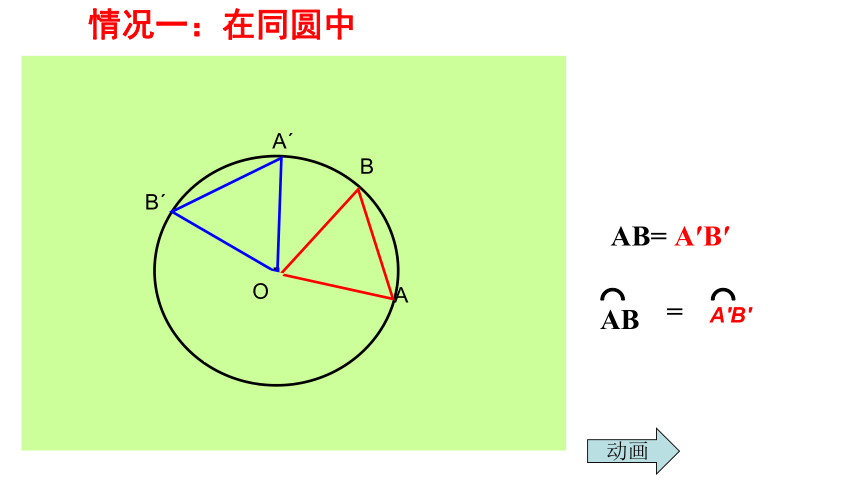
情况一:在同圆中
·
Aˊ
Bˊ
A
B
O
AB= A′B′
⌒
AB
⌒
A′B′
=
动画
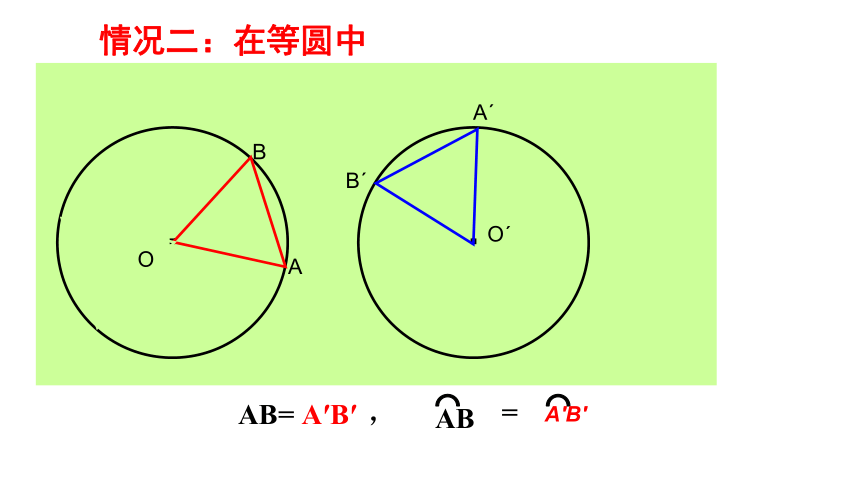
情况二:在等圆中
AB= A′B′ ,
⌒
AB
⌒
A′B′
=
·
O
A
B
·
Oˊ
Aˊ
Bˊ
·
O
A
B
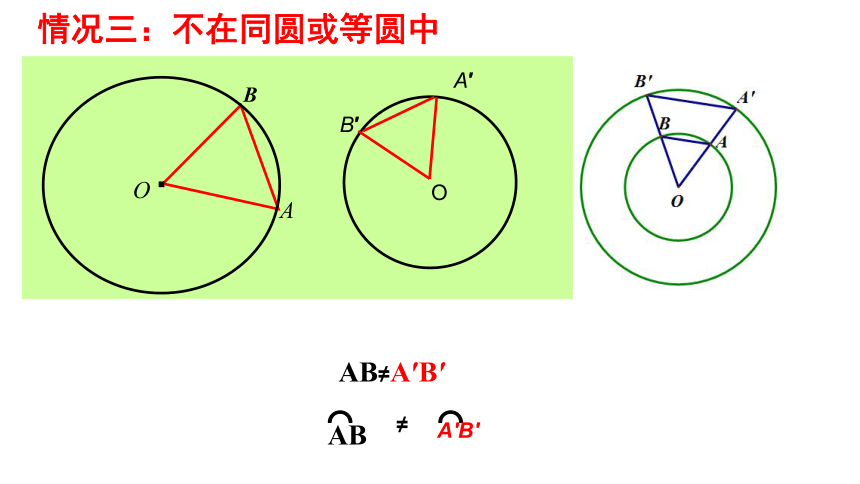
情况三:不在同圆或等圆中
B′
A′
O
AB≠A′B′
⌒
AB
⌒
A′B′
≠
定理:在同圆或等圆中,相等的圆心角所对
的弧相等,所对的弦也相等.
注意:定理中前提条件在同圆或等圆中不能去掉.
2.你能用文字语言归纳你得到的结论吗?
在同圆或等圆中
3.如图,你能用几何语言表述弧、弦、圆心角
关系定理吗?
∵∠AOB =∠AˊOBˊ
∴AB= A′B′ ,
⌒
AB
⌒
A′B′
=
·
A
B
O
Bˊ
Aˊ
(1)画两条等弧,它们所对的圆心角,所对的弦有什么关系?
探究二
合作交流 探究新知
(2)你能用文字语言归纳你得到的结论吗?请归纳.
合作交流 探究新知
探究三
(1)画两条等弦,它们所对圆心角,所对的弧有什么关系?
(2)你能用文字语言归纳你得到的结论吗?请归纳,并与同学交流.
动画
合作交流 探究新知
推论:在同圆或等圆中,相等的弦所对的圆心角相等,所对的优弧和劣弧分别相等.
推论:在同圆或等圆中,相等的弧所对的圆心角相等,
所对的弦也相等.
思考:通过以上的探究,两个圆心角,两条弧,两条弦
中如果有一组量相等,则它们所对应的其余各组量有什
么关系?
在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量对应相等,则它们所对应的其余各组量都
相等。
归纳总结
弦
圆心角
弧
整体理解
∴AB=AC, △ABC 等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形,
AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
证明:∵AB=AC
⌒
⌒
例题讲解 运用新知
当堂演练 巩固新知
。
1.已知:如图所示,AD=BC.求证:AB=CD
变式练习2:如图,AB是直径,BC=AD,∠DOC=60°,
求∠BOC的度数.
变式练习1:已知:如图所示,AB=CD.求证:AD=BC.
1.回顾整节课,你学到了哪些知识?你掌握了哪些数学思想方法?
归纳反思 拓展延伸
2.作业布置:
(1)课本P85练习第1题,第2题.
(2)整理导学案
如图,AB、CD是⊙O的两条弦.AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
拓展延伸
结论拓展:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量对应相等,则它们所对应的其余各组量都相等。
教师寄语:
带着梦,向前冲,
不要怕,放轻松。
努力去追梦,
愿你更成功!
人教版九年级上册
24.1 弧、弦、圆心角
古希腊数学家这样描述圆:
在一切平面图形中,圆是最美的!
1.圆是中心对称图形吗 它的对称中心在哪里
把圆绕圆心旋转任意一个角度后,你发现了什么?
.
动画
圆是中心对称图形,它的对称中心是圆心.
定理:把圆绕圆心旋转任意一个角度后,仍与
原来的圆重合.
创设情境 导入新课
圆心角:我们把顶点在圆心的角叫做圆心角.
以下四个角中是圆心角的是( )
创设情境 导入新课
C
(1)画两个相等的圆心角,观察它们所对的弧,弦有什么关系?
探究一
合作交流 探究新知
活动要求:①独立画图,在图上标上相应的字母.
②画好图后,小组交流所画的图.
③小组交流所得到的关系.
情况一:在同圆中
·
Aˊ
Bˊ
A
B
O
AB= A′B′
⌒
AB
⌒
A′B′
=
动画
情况二:在等圆中
AB= A′B′ ,
⌒
AB
⌒
A′B′
=
·
O
A
B
·
Oˊ
Aˊ
Bˊ
·
O
A
B
情况三:不在同圆或等圆中
B′
A′
O
AB≠A′B′
⌒
AB
⌒
A′B′
≠
定理:在同圆或等圆中,相等的圆心角所对
的弧相等,所对的弦也相等.
注意:定理中前提条件在同圆或等圆中不能去掉.
2.你能用文字语言归纳你得到的结论吗?
在同圆或等圆中
3.如图,你能用几何语言表述弧、弦、圆心角
关系定理吗?
∵∠AOB =∠AˊOBˊ
∴AB= A′B′ ,
⌒
AB
⌒
A′B′
=
·
A
B
O
Bˊ
Aˊ
(1)画两条等弧,它们所对的圆心角,所对的弦有什么关系?
探究二
合作交流 探究新知
(2)你能用文字语言归纳你得到的结论吗?请归纳.
合作交流 探究新知
探究三
(1)画两条等弦,它们所对圆心角,所对的弧有什么关系?
(2)你能用文字语言归纳你得到的结论吗?请归纳,并与同学交流.
动画
合作交流 探究新知
推论:在同圆或等圆中,相等的弦所对的圆心角相等,所对的优弧和劣弧分别相等.
推论:在同圆或等圆中,相等的弧所对的圆心角相等,
所对的弦也相等.
思考:通过以上的探究,两个圆心角,两条弧,两条弦
中如果有一组量相等,则它们所对应的其余各组量有什
么关系?
在同圆或等圆中,如果两个圆心角、两条弧、两条弦
中有一组量对应相等,则它们所对应的其余各组量都
相等。
归纳总结
弦
圆心角
弧
整体理解
∴AB=AC, △ABC 等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形,
AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
证明:∵AB=AC
⌒
⌒
例题讲解 运用新知
当堂演练 巩固新知
。
1.已知:如图所示,AD=BC.求证:AB=CD
变式练习2:如图,AB是直径,BC=AD,∠DOC=60°,
求∠BOC的度数.
变式练习1:已知:如图所示,AB=CD.求证:AD=BC.
1.回顾整节课,你学到了哪些知识?你掌握了哪些数学思想方法?
归纳反思 拓展延伸
2.作业布置:
(1)课本P85练习第1题,第2题.
(2)整理导学案
如图,AB、CD是⊙O的两条弦.AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
拓展延伸
结论拓展:
在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量对应相等,则它们所对应的其余各组量都相等。
教师寄语:
带着梦,向前冲,
不要怕,放轻松。
努力去追梦,
愿你更成功!
同课章节目录
