物理多媒体教学课件:3.实验 探究弹力和弹簧伸长的关系(人教版必修1)
文档属性
| 名称 | 物理多媒体教学课件:3.实验 探究弹力和弹簧伸长的关系(人教版必修1) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2013-03-28 13:39:51 | ||
图片预览






文档简介
课件27张PPT。实验 探究弹力和弹簧
伸长的关系1.探究弹力和弹簧伸长量之间的关系.
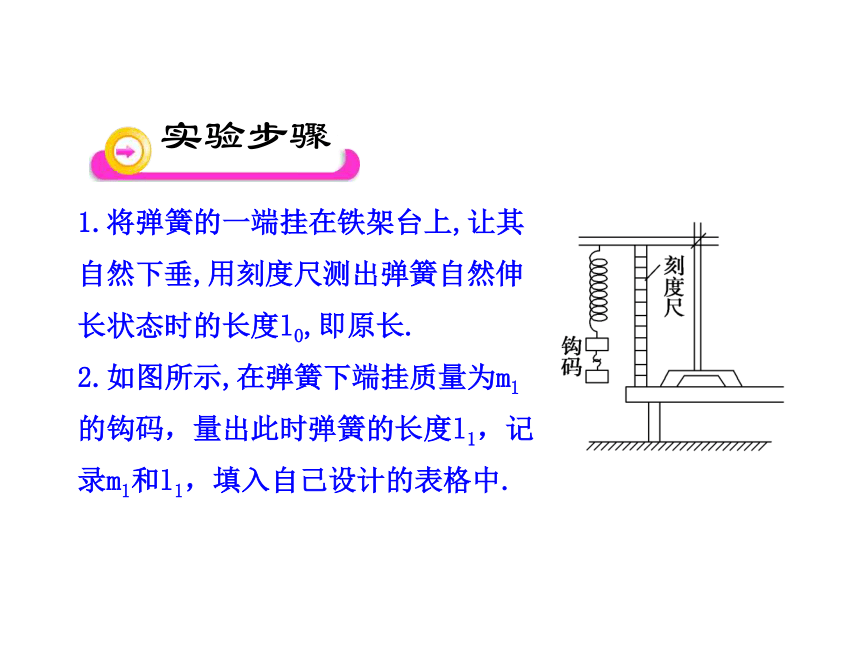
2.学会利用图象法处理实验数据.1.如图所示,在弹簧下端悬挂钩码时弹簧
会伸长,平衡时弹簧产生的弹力与所挂钩
码的重力大小相等.
2.弹簧的长度可用刻度尺直接测出,伸长
量可以由拉长后的长度减去弹簧原来的长
度进行计算.这样就可以研究弹簧的弹力和弹簧伸长量之间的定量关系了.铁架台、弹簧、毫米刻度尺、钩码若干、三角板、坐标纸、重垂线、铅笔. 1.将弹簧的一端挂在铁架台上,让其
自然下垂,用刻度尺测出弹簧自然伸
长状态时的长度l0,即原长.
2.如图所示,在弹簧下端挂质量为m1
的钩码,量出此时弹簧的长度l1,记
录m1和l1,填入自己设计的表格中.3.改变所挂钩码的质量,量出对应的弹簧长度,记录m2、m3、m4、m5和相应的弹簧长度l2、l3、l4、l5,并得出每次弹簧的伸长量x1、x2、x3、x4、x5.1.以弹力F(大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x为横坐标,用描点法作图.连接各点,得出弹力F随弹簧伸长量x变化的图线.
2.以弹簧的伸长量为自变量,写出曲线所代表的函数.首先尝试一次函数,如果不行则考虑二次函数.
3.得出弹力和弹簧伸长之间的定量关系,解释函数表达式中常数的物理意义.1.弹簧拉力大小的不稳定会造成误差.因此,使弹簧的悬挂端固定,另一端通过悬挂钩码来充当对弹簧的拉力,待稳定后再读数可以提高实验的准确度.
2.尽量精确地测量弹簧的长度,也是减小实验误差的基本方法.
3.描点、作图不准确. 1.所挂钩码不要过重,以免弹簧被过分拉伸,超出它的弹性限度.要注意观察,适可而止.
2.每次所挂钩码的质量差尽量大一些,从而使坐标上描的点的间距尽可能大,这样作出的图线更精确.
3.测弹簧长度时,一定要在弹簧竖直悬挂且处于平衡状态时测量,以免增大误差.
4.描点画线时,所描的点不一定都落在曲线上,但应注意一定要使各点均匀分布在曲线的两侧.
5.记录数据时要注意弹力及弹簧伸长量的对应关系及单位. 【例1】某同学用如图所示装置做探究弹力
和弹簧伸长关系的实验.他先测出不挂砝码
时弹簧下端指针所指的标尺刻度,然后在弹
簧下端挂上砝码,并逐个增加砝码,测出指
针所指的标尺刻度,所得数据列表如下:(重
力加速度g=9.8 m/s2) (1)根据所测数据,在坐标纸上作出
弹簧指针所指的标尺刻度x与砝码
质量m的关系曲线.
(2)根据所测得的数据和关系曲线可
以判断,在_____范围内,弹力大小与
弹簧伸长关系满足胡克定律.这种规
格弹簧劲度系数为________N/m. 思路点拨
(1)在坐标纸上描点,然后根据各点的分布与走向,用平滑的曲线(或直线)连接各点.
(2)满足胡克定律的应是图形中的直线部分.
解析:(1)如图所示 (2)根据图形可以看出,当m≤5.00×102 g=0.5 kg时,
标尺刻度x与砝码质量m成一次函数关系,所以当F=mg
≤4.9 N范围内弹力大小与弹簧伸长关系满足胡克定律.
图线斜率的大小在数值上等于弹簧的劲度系数k,则k=
25 N/m.
答案:(1)见解析 (2)0~4.9 N 25 【例2】用一个支架、一根弹簧、一把直尺和一个已知质量的钩码,来测定某个不太重的物体有多重,该怎么做?
解析:本题主要考查实验方法的拓展迁移能力.
(1)将弹簧上端固定在支架上,下端挂上钩码(质量已知为m),测出弹簧伸长量x.
(2)将钩码取下换上待测物体,测出弹簧伸长量x′.
(3)求出待测物体的重力【例2】(1)在“探究弹力和弹簧伸长的关系”实验中,以下说法正确的是( )
A.弹簧被拉伸时,不能超出它的弹性限度
B.用增加悬挂钩码的方法给弹簧施加拉力,应保证弹簧位于竖直位置且处于平衡状态
C.用直尺测得弹簧的长度即为弹簧的伸长量
D.用几个不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比相等(2)某同学做“探究弹力和弹簧伸长的关系”的实验,他
先把弹簧平放在桌面上使其自然伸长,用直尺测出弹簧
的原长L0,再把弹簧竖直悬挂起来,挂上钩码后测出弹簧
伸长后的长度L,把L-L0作为弹簧的伸长量x,这样操作,
由于弹簧自身重力的影响,最后画出的图线可能是下图
中的( )(2)由表可看出,材料一定长,一定截面积时,拉力与伸长量的比例为定值.
设1 m长,截面积为0.05 cm2的比例系数为K1
2 m长,截面积为0.05 cm2的比例系数为K2
1 m长,截面积为0.10 cm2的比例系数为K3 1.如图5甲所示,一个弹簧一端固定在传感器上,传感器与
电脑相连.当对弹簧施加变化的作用力(拉力或压力)时,
在电脑上得到了弹簧形变量与弹簧产生的弹力大小的关系
图象(如图乙).则下列判断正确的是( )
图5A.弹簧产生的弹力和弹簧的长度成正比
B.弹簧长度的增加量与对应的弹力增加量成正比
C.该弹簧的劲度系数是200 N/m
D.该弹簧受到反向压力时,劲度系数不变
【解析】由乙图可知F=kx,即弹簧的弹力和弹簧的形变
量成正比,不与弹簧长度成正比,A错误.由ΔF=kΔx可
知,B说法正确;由 ,C正确;F-x图线
的斜率对应弹簧的劲度系数,而x>0和x<0时的斜率相同,
故D正确. 2.某同学在做“探究弹力和弹簧伸长量的关系”实验中,
他先把弹簧平放在桌面上使其自然伸长,用直尺测出弹
簧的原长l0,再把弹簧竖直悬挂起来,挂上钩码后测出弹
簧伸长后的长度l,把l-l0作为弹簧的伸长量x.这样操作,由于弹簧自身重力的影响,最后画出的图线可能是下图中的哪一个( )
【解析】由于考虑弹簧自身重力的影响,当不挂钩码
时,弹簧的伸长量x≠0,所以选C. C3.做“探究弹力和弹簧伸长量的关系”的实验步骤如下:
A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连接起来.
B.记下弹簧不挂钩码时其下端在刻度尺上的刻度L0;
C.将铁架台固定于桌子上(也可在横梁的另一侧挂上一定的配重),并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺;
D.依次在弹簧下端挂上2个、3个、4个…钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码; E.以弹簧伸长量为自变量,写出弹力与伸长量的关系式,首先尝试写成一次函数,如果不行则考虑二次函数;
F.解释函数表达式中常数的物理意义;
G.整理仪器.
请将以上步骤按操作的先后顺序排列出来:__________.
【解析】根据实验的实验操作过程应先安装仪器,再挂钩码然后记录数据,分析数据,最后整理即可,排列先后顺序为:CBDAEFG. 4.某同学在研究学习中,利用所学的知识解决了如下问题:一轻弹簧竖直悬挂在某一深度为h=25.0cm,且开口向下的小筒中(没有外力作用时弹簧的下部分位于筒内,但测力计可以与弹簧的下端接触),如图6甲所示.如果本实验的长度测量工具只能测出筒的下端弹簧的长度L.现要测出弹簧的原长L0和弹簧的劲度系数,该同学通过改变L而测出对应的弹力F,作出F-L变化的图线如图6乙所示,则弹簧的劲度系数为_______N/m,弹簧的原长L0=________cm. 【解析】根据胡克定律F=k(h+L-L0)=kL+k(h-L0),从图
中知道当L=0时,F=10N;当L=10cm时,F=20N;将其代入方程联立得k=100N/m,L0=15.0cm.
答案:100 15.0图65.用纳米技术处理过的材料叫纳米材料,其性质与处理前相比会发生很多变化.如机械性能会成倍地增加,对光的反射能力会变得很低,熔点会大大地降低,甚至有特殊的磁性质.现有一纳米合金丝,欲测出其伸长量x与所受到的拉力F、长度L、截面直径D的关系.
(1)测量上述物理量需要的主要器材是:_____、_____、______等.
(2)若实验中测量的数据如下表,根据这些数据请写出x与F、L、D间的关系式:x=_________.(若用到比例系数,可用k表示) 拉力F/N伸长量x/cm直径D/mm(3)在研究并得到上述关系的过程中,主要运用的科学研究方法是____________________(只需写出一种).
(4)若有一根合金丝的长度为20cm,截面直径为0.200mm,使用中要求其伸长量不能超过原长的百分之一,那么这根合金丝能承受的最大拉力为______N.【解析】(2)由题目所给的数据分析可知:当力、直径
一定时,伸长量与长度成正比,当力、长度一定时,伸
长量与直径成反比,当长度、直径一定时,伸长量与
力成正比,有:x=kFL/D(取一组数据验证,式中的系数
不为零)
答案:(1)弹簧测力计 刻度尺 螺旋测微器
(3)控制变量法 (4)625
伸长的关系1.探究弹力和弹簧伸长量之间的关系.
2.学会利用图象法处理实验数据.1.如图所示,在弹簧下端悬挂钩码时弹簧
会伸长,平衡时弹簧产生的弹力与所挂钩
码的重力大小相等.
2.弹簧的长度可用刻度尺直接测出,伸长
量可以由拉长后的长度减去弹簧原来的长
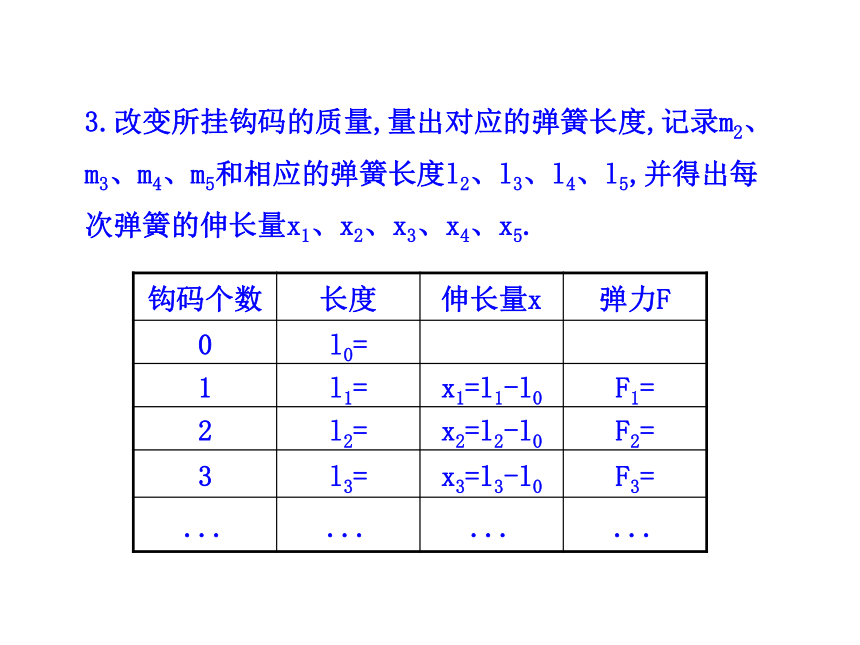
度进行计算.这样就可以研究弹簧的弹力和弹簧伸长量之间的定量关系了.铁架台、弹簧、毫米刻度尺、钩码若干、三角板、坐标纸、重垂线、铅笔. 1.将弹簧的一端挂在铁架台上,让其
自然下垂,用刻度尺测出弹簧自然伸
长状态时的长度l0,即原长.
2.如图所示,在弹簧下端挂质量为m1
的钩码,量出此时弹簧的长度l1,记
录m1和l1,填入自己设计的表格中.3.改变所挂钩码的质量,量出对应的弹簧长度,记录m2、m3、m4、m5和相应的弹簧长度l2、l3、l4、l5,并得出每次弹簧的伸长量x1、x2、x3、x4、x5.1.以弹力F(大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x为横坐标,用描点法作图.连接各点,得出弹力F随弹簧伸长量x变化的图线.
2.以弹簧的伸长量为自变量,写出曲线所代表的函数.首先尝试一次函数,如果不行则考虑二次函数.
3.得出弹力和弹簧伸长之间的定量关系,解释函数表达式中常数的物理意义.1.弹簧拉力大小的不稳定会造成误差.因此,使弹簧的悬挂端固定,另一端通过悬挂钩码来充当对弹簧的拉力,待稳定后再读数可以提高实验的准确度.
2.尽量精确地测量弹簧的长度,也是减小实验误差的基本方法.
3.描点、作图不准确. 1.所挂钩码不要过重,以免弹簧被过分拉伸,超出它的弹性限度.要注意观察,适可而止.
2.每次所挂钩码的质量差尽量大一些,从而使坐标上描的点的间距尽可能大,这样作出的图线更精确.
3.测弹簧长度时,一定要在弹簧竖直悬挂且处于平衡状态时测量,以免增大误差.
4.描点画线时,所描的点不一定都落在曲线上,但应注意一定要使各点均匀分布在曲线的两侧.
5.记录数据时要注意弹力及弹簧伸长量的对应关系及单位. 【例1】某同学用如图所示装置做探究弹力
和弹簧伸长关系的实验.他先测出不挂砝码
时弹簧下端指针所指的标尺刻度,然后在弹
簧下端挂上砝码,并逐个增加砝码,测出指
针所指的标尺刻度,所得数据列表如下:(重
力加速度g=9.8 m/s2) (1)根据所测数据,在坐标纸上作出
弹簧指针所指的标尺刻度x与砝码
质量m的关系曲线.
(2)根据所测得的数据和关系曲线可
以判断,在_____范围内,弹力大小与
弹簧伸长关系满足胡克定律.这种规
格弹簧劲度系数为________N/m. 思路点拨
(1)在坐标纸上描点,然后根据各点的分布与走向,用平滑的曲线(或直线)连接各点.
(2)满足胡克定律的应是图形中的直线部分.
解析:(1)如图所示 (2)根据图形可以看出,当m≤5.00×102 g=0.5 kg时,
标尺刻度x与砝码质量m成一次函数关系,所以当F=mg
≤4.9 N范围内弹力大小与弹簧伸长关系满足胡克定律.
图线斜率的大小在数值上等于弹簧的劲度系数k,则k=
25 N/m.
答案:(1)见解析 (2)0~4.9 N 25 【例2】用一个支架、一根弹簧、一把直尺和一个已知质量的钩码,来测定某个不太重的物体有多重,该怎么做?
解析:本题主要考查实验方法的拓展迁移能力.
(1)将弹簧上端固定在支架上,下端挂上钩码(质量已知为m),测出弹簧伸长量x.
(2)将钩码取下换上待测物体,测出弹簧伸长量x′.
(3)求出待测物体的重力【例2】(1)在“探究弹力和弹簧伸长的关系”实验中,以下说法正确的是( )
A.弹簧被拉伸时,不能超出它的弹性限度
B.用增加悬挂钩码的方法给弹簧施加拉力,应保证弹簧位于竖直位置且处于平衡状态
C.用直尺测得弹簧的长度即为弹簧的伸长量
D.用几个不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比相等(2)某同学做“探究弹力和弹簧伸长的关系”的实验,他
先把弹簧平放在桌面上使其自然伸长,用直尺测出弹簧
的原长L0,再把弹簧竖直悬挂起来,挂上钩码后测出弹簧
伸长后的长度L,把L-L0作为弹簧的伸长量x,这样操作,
由于弹簧自身重力的影响,最后画出的图线可能是下图
中的( )(2)由表可看出,材料一定长,一定截面积时,拉力与伸长量的比例为定值.
设1 m长,截面积为0.05 cm2的比例系数为K1
2 m长,截面积为0.05 cm2的比例系数为K2
1 m长,截面积为0.10 cm2的比例系数为K3 1.如图5甲所示,一个弹簧一端固定在传感器上,传感器与
电脑相连.当对弹簧施加变化的作用力(拉力或压力)时,
在电脑上得到了弹簧形变量与弹簧产生的弹力大小的关系
图象(如图乙).则下列判断正确的是( )
图5A.弹簧产生的弹力和弹簧的长度成正比
B.弹簧长度的增加量与对应的弹力增加量成正比
C.该弹簧的劲度系数是200 N/m
D.该弹簧受到反向压力时,劲度系数不变
【解析】由乙图可知F=kx,即弹簧的弹力和弹簧的形变
量成正比,不与弹簧长度成正比,A错误.由ΔF=kΔx可
知,B说法正确;由 ,C正确;F-x图线
的斜率对应弹簧的劲度系数,而x>0和x<0时的斜率相同,
故D正确. 2.某同学在做“探究弹力和弹簧伸长量的关系”实验中,
他先把弹簧平放在桌面上使其自然伸长,用直尺测出弹
簧的原长l0,再把弹簧竖直悬挂起来,挂上钩码后测出弹
簧伸长后的长度l,把l-l0作为弹簧的伸长量x.这样操作,由于弹簧自身重力的影响,最后画出的图线可能是下图中的哪一个( )
【解析】由于考虑弹簧自身重力的影响,当不挂钩码
时,弹簧的伸长量x≠0,所以选C. C3.做“探究弹力和弹簧伸长量的关系”的实验步骤如下:
A.以弹簧伸长量为横坐标,以弹力为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连接起来.
B.记下弹簧不挂钩码时其下端在刻度尺上的刻度L0;
C.将铁架台固定于桌子上(也可在横梁的另一侧挂上一定的配重),并将弹簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺;
D.依次在弹簧下端挂上2个、3个、4个…钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码; E.以弹簧伸长量为自变量,写出弹力与伸长量的关系式,首先尝试写成一次函数,如果不行则考虑二次函数;
F.解释函数表达式中常数的物理意义;
G.整理仪器.
请将以上步骤按操作的先后顺序排列出来:__________.
【解析】根据实验的实验操作过程应先安装仪器,再挂钩码然后记录数据,分析数据,最后整理即可,排列先后顺序为:CBDAEFG. 4.某同学在研究学习中,利用所学的知识解决了如下问题:一轻弹簧竖直悬挂在某一深度为h=25.0cm,且开口向下的小筒中(没有外力作用时弹簧的下部分位于筒内,但测力计可以与弹簧的下端接触),如图6甲所示.如果本实验的长度测量工具只能测出筒的下端弹簧的长度L.现要测出弹簧的原长L0和弹簧的劲度系数,该同学通过改变L而测出对应的弹力F,作出F-L变化的图线如图6乙所示,则弹簧的劲度系数为_______N/m,弹簧的原长L0=________cm. 【解析】根据胡克定律F=k(h+L-L0)=kL+k(h-L0),从图
中知道当L=0时,F=10N;当L=10cm时,F=20N;将其代入方程联立得k=100N/m,L0=15.0cm.
答案:100 15.0图65.用纳米技术处理过的材料叫纳米材料,其性质与处理前相比会发生很多变化.如机械性能会成倍地增加,对光的反射能力会变得很低,熔点会大大地降低,甚至有特殊的磁性质.现有一纳米合金丝,欲测出其伸长量x与所受到的拉力F、长度L、截面直径D的关系.
(1)测量上述物理量需要的主要器材是:_____、_____、______等.
(2)若实验中测量的数据如下表,根据这些数据请写出x与F、L、D间的关系式:x=_________.(若用到比例系数,可用k表示) 拉力F/N伸长量x/cm直径D/mm(3)在研究并得到上述关系的过程中,主要运用的科学研究方法是____________________(只需写出一种).
(4)若有一根合金丝的长度为20cm,截面直径为0.200mm,使用中要求其伸长量不能超过原长的百分之一,那么这根合金丝能承受的最大拉力为______N.【解析】(2)由题目所给的数据分析可知:当力、直径
一定时,伸长量与长度成正比,当力、长度一定时,伸
长量与直径成反比,当长度、直径一定时,伸长量与
力成正比,有:x=kFL/D(取一组数据验证,式中的系数
不为零)
答案:(1)弹簧测力计 刻度尺 螺旋测微器
(3)控制变量法 (4)625
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
