七年级数学下《相交线与平行线》导学案
文档属性
| 名称 | 七年级数学下《相交线与平行线》导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 956.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-28 00:00:00 | ||
图片预览



文档简介
第五章 相交线与平行线
第1课时:5.1.1 相交线 导学案
班级: 姓名:
【学习目标】了解邻补角、对顶角, 能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些问题.
【学习重点】邻补角、对顶角的概念,对顶角性质与应用.?
【学习难点】理解对顶角相等的性质.
【学习过程】
一、学前准备
各小组对七年级上学过的直线、射线、线段、角做总结.每人写一个总结小报告,并编写两道与它们相关的题目,在小组交流,并推出小组最好的两道题在班级汇报.
二、探索思考
探索一:完成课本P2页的探究,填在课本上.
你能归纳出“邻补角”的定义吗? .
“对顶角”的定义呢? .
练习一:
1.如图1所示,直线AB和CD相交于点O,OE是一条射线.
(1)写出∠AOC的邻补角:____ _ ___ __;
(2)写出∠COE的邻补角: __;
(3)写出∠BOC的邻补角:____ _ ___ __;
(4)写出∠BOD的对顶角:____ _.
2.如图所示,∠1与∠2是对顶角的是( )
探索二:任意画一对对顶角,量一量,算一算,它们相等吗?如果相等,请说明理由.
请归纳“对顶角的性质”: .
练习二:
1.如图,直线a,b相交,∠1=40°,则∠2=_______∠3=_______∠4=_______
2.如图直线AB、CD、EF相交于点O,∠BOE的对顶角是______,∠COF 的邻补角是____,若∠AOE=30°,那么∠BOE=_______,∠BOF=_______
3.如图,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠EOF=_____.
三、当堂反馈
1.若两个角互为邻补角,则它们的角平分线所夹的角为 度.
2.如图所示,直线a,b,c两两相交,∠1=60°,∠2=∠4,求∠3、∠5的度数.
3.如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,你能说出所量的角是多少度吗?你的根据是什么?
4.探索规律:
(1)两条直线交于一点,有 对对顶角;
(2)三条直线交于一点,有 对对顶角;
(3)四条直线交于一点,有 对对顶角;
(4)n条直线交于一点,有 对对顶角.
四、学习反思
本节课你有哪些收获?
第2课时 5.1.2 垂线 导学案
班级: 姓名:
【学习目标】1了解垂线、点到直线的距离的意义,理解垂线和垂线段的性质;
2会用三角板过一点画已知直线的垂线,并会度量点到直线的距离.
【学习重点】垂线的意义、性质和画法,垂线段性质及其简单应用.?
【学习难点】垂线的画法以及对点到直线的距离的概念的理解.
【学习过程】
一、学前准备
在学习对顶角知识的时候,我们认识了“两线四角”,及两条直线相交于一点,得到四个角,这四个角里面,有两对对顶角,它们分别对应相等,如图,可以说成“直线AB与CD相交于点O”.
我们如果把直线CD绕点O旋转,无论是按照顺时针方向转,还是按照逆时针方向转,∠BOD的大小都将发生变化.
当两条直线相交所成的四个角中有一个为直角时,叫做这两条直线互相垂直,其中的一条直线叫垂线,它们的交点叫垂足.如图
用几何语言表示:
方式⑴∵ ∠AOC=90° ∴ AB_____CD,垂足是_____
方式⑵∵ AB⊥CD于O ∴ ∠AOC=______
二、探索思考
探索一:请你认真画一画,看看有什么收获.
⑴如图1,利用三角尺或量角器画已知直线的垂线,这样的垂线能画__________条;
⑵如图2,经过直线上一点A画的垂线,这样的垂线能画_____条;
⑶如图3,经过直线外一点B画的垂线,这样的垂线能画_____条;
(图1) (图2) (图3a) (图3b)
经过探索,我们可以发现:在同一平面内,过一点有且只有_____条直线与已知直线垂直.
练习一:
1.如图所示,OA⊥OB,OC是一条射线,若∠AOC=120°,
求∠BOC度数
2.如图所示,直线AB⊥CD于点O,直线EF经过点O,
若∠1=26°,求∠2的度数.
3.如图所示,直线AB,CD相交于点O,P是CD上一点.
(1)过点P画AB的垂线PE,垂足为E.
(2)过点P画CD的垂线,与AB相交于F点.
(3)比较线段PE,PF,PO三者的大小关系
探索二:仔细观察测量比较上题中点P分别到直线AB上三点E、F、O的距离,你还有什么收获?请将你的收获记录下来:_______________________________________________
简单说成: .还有,直线外一点到这条直线的垂线段的 叫做点到直线的距离.注意:垂线是 ,垂线段是一条 ,点到直线的距离是一个数量,不能说“垂线段”是距离.
练习二:
1.在下列语句中,正确的是( ).
A.在同一平面内,一条直线只有一条垂线
B.在同一平面内,过直线上一点的直线只有一条
C.在同一平面内,过直线上一点且垂直于这条直线的直线有且只有一条
D.在同一平面内,垂线段就是点到直线的距离
2.如图所示,AC⊥BC,CD⊥AB于D,AC=5cm,BC=12cm,AB=13cm,则点B到AC的距离是________,点A到BC的距离是_______,点C到AB的距离是_______,AC>CD的依据是_________.
三、当堂反馈
1.如图所示AB,CD相交于点O,EO⊥AB于O,FO⊥CD于O,∠EOD与∠FOB的大小关系是( )
A.∠EOD比∠FOB大 B.∠EOD比∠FOB小
C.∠EOD与∠FOB相等 D.∠EOD与∠FOB大小关系不确定
2.如图,一辆汽车在直线形的公路AB上由A向B行驶,C,D是分别位于公路AB两侧的加油站.设汽车行驶到公路AB上点M的位置时,距离加油站C最近;行驶到点N的位置时,距离加油站D最近,请在图中的公路上分别画出点M,N的位置并说明理由.
3.如图,AOB为直线,∠AOD:∠DOB=3:1,OD平分∠COB. (1)求∠AOC的度数;(2)判断AB与OC的位置关系.
四、学习反思
本节课你有哪些收获?
第3课时5.1.3 同位角、内错角、同旁内角 导学案
班级: 姓名:
【学习目标】1使学生理解三线八角的意义,并能从复杂图形中识别它们;
2通过三线八角的特点的分析,培养学生抽象概括问题的能力.
【学习重点】三线八角的意义,以及如何在各种变式的图形中找出这三类角.?
【学习难点】能准确在各种变式的图形中找出这三类角.
【学习过程】
一、学前准备
在前面我们学习了两条直线相交于一点,得到四个角,即“两线四角”,这四个角里面,有 对对顶角,有 对邻补角.如果是一条直线分别与两条直线相交,结果又会怎样呢?
二、探索思考
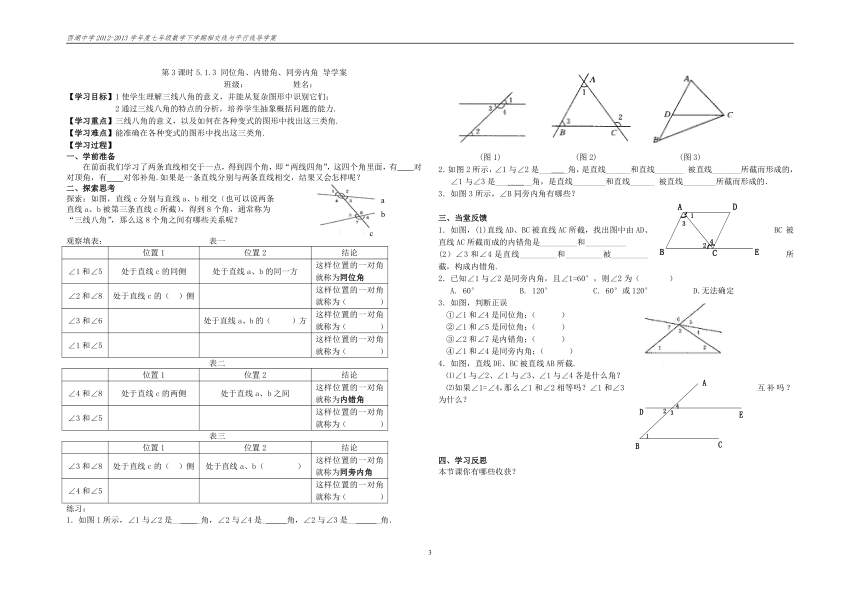
探索:如图,直线c分别与直线a、b相交(也可以说两条
直线a、b被第三条直线c所截),得到8个角,通常称为
“三线八角”,那么这8个角之间有哪些关系呢?
观察填表: 表一
位置1
位置2
结论
∠1和∠5
处于直线c的同侧
处于直线a、b的同一方
这样位置的一对角就称为同位角
∠2和∠8
处于直线c的( )侧
这样位置的一对角就称为( )
∠3和∠6
处于直线a、b的( )方
这样位置的一对角就称为( )
∠1和∠5
这样位置的一对角就称为( )
表二
位置1
位置2
结论
∠4和∠8
处于直线c的两侧
处于直线a、b之间
这样位置的一对角就称为内错角
∠3和∠5
这样位置的一对角就称为( )
表三
位置1
位置2
结论
∠3和∠8
处于直线c的( )侧
处于直线a、b( )
这样位置的一对角就称为同旁内角
∠4和∠5
这样位置的一对角就称为( )
练习:
1.如图1所示,∠1与∠2是__ _角,∠2与∠4是_ 角,∠2与∠3是__ _角.
(图1) (图2) (图3)
2.如图2所示,∠1与∠2是___ _角,是直线______和直线_______被直线_______所截而形成的,∠1与∠3是___ __角,是直线________和直线______被直线________所截而形成的.
3.如图3所示,∠B同旁内角有哪些?
三、当堂反馈
1.如图,(1)直线AD、BC被直线AC所截,找出图中由AD、BC被直线AC所截而成的内错角是_________和__________
(2)∠3和∠4是直线_________和_________被_________所截,构成内错角.
2.已知∠1与∠2是同旁内角,且∠1=60°,则∠2为( )
A. 60° B. 120° C. 60°或120° D.无法确定
3.如图,判断正误
①∠1和∠4是同位角;( )
②∠1和∠5是同位角;( )
③∠2和∠7是内错角;( )
④∠1和∠4是同旁内角;( )
4.如图,直线DE、BC被直线AB所截.
⑴∠1与∠2、∠1与∠3、∠1与∠4各是什么角?
⑵如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
四、学习反思
本节课你有哪些收获?
第4课时5.2.1 平行线 导学案
班级: 姓名:
【学习目标】1使学生知道平行线的概念,掌握平行公理;
2了解平行线具有传递性,能够画出已知直线的平行线.
【学习重点】平行线的概念和平行公理,利用直尺和三角板画已知直线的平行线.?
【学习难点】用几何语言描述画图过程,根据几何语言画出图形.
【学习过程】
一、学前准备
在上学期我们学过点和直线的位置关系,同学们还记得点和直线有几种位置关系吗?请画出来,并尝试用几何语言来表示.
二、探索思考
探索一:我们知道,火车行驶的两条笔直的铁轨、人行道上的斑马线等都给我们平行的形象.一般地,在同一平面内,不相交的两条直线叫做平行线.如图,记作“∥”或“AB∥CD”,读作“直线平行于直线”.请同学们思考一下:在同一平面内,两条不重合的直线有几种位置关系?动手画一画,并尝试用几何语言来表示..
练习一:
1.下列说法中,正确的是( ).
A.两直线不相交则平行 B.两直线不平行则相交
C.若两线段平行,那么它们不相交 D.两条线段不相交,那么它们平行
2.在同一平面内,有三条直线,其中只有两条是平行的,那么交点有( ).
A.0个 B.1个 C.2个 D.3个
探索二:请同学们仔细阅读课本P13页“平行线的讨论”,认真思考.通过观察和画图,可以体验一个基本事实(平行公理):经过直线外一点, 一条直线与这条直线平行.
同样,我们还有(平行线的传递性):如果两条直线都与第三条直线平行,那么这两条直线也互相平行.简单的说就是:平行于同一直线的两直线平行.
用几何语言可表示为:如果∥,∥,那么 .
练习二:
1.如图1所示,与AB平行的棱有_______条,与AA′平行的棱有_____条.
2.如图2所示,按要求画平行线.
(1)过P点画AB的平行线EF;(2)过P点画CD的平行线MN.
3.如图3所示,点A,B分别在直线,上,(1)过点A画到的垂线段;(2)过点B画直线∥.
(图1) (图2) (图3)
4.下列说法中,错误的有( ).
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,那么a∥c;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂线三种
A.3个 B.2个 C.1个 D.0个
三、当堂反馈
1.在同一平面内,一条直线和两条平行线中一条直线相交,那么这条直线与平行线中的另一边必__________.
2.同一平面内,两条相交直线不可能与第三条直线都平行,这是因为________________.
3.判断题
(1)不相交的两条直线叫做平行线.( )
(2)在同一平面内,不相交的两条射线是平行线.( )
(3)如果一条直线与两条平行线中的一条平行, 那么它与另一条也互相平行.( )
4.读下列语句,并画出图形:
⑴点P是直线AB外一点,直线CD经过点P,且与直线AB平行,直线EF也经过点P且与直线AB垂直.
⑵直线AB,CD是相交直线,点P是直线AB,CD外一点,直线EF经过点P且与直线AB平行,与直线CD相交于E.
四、学习反思
本节课你有哪些收获?
第5课时5.2.2 平行线的判定 导学案
班级: 姓名:
【学习目标】使学生掌握平行线的判定,并能应用这些知识判断两条直线是否平行,培养学生简单的推理能力.
【学习重点】平行线的三种判定方法,并运用这三种方法判断两直线平行.?
【学习难点】运用平行线的判定方法进行简单的推理.
【学习过程】
一、学前准备
还知道“三线八角”吗?请画一画,找出一组同位角、一组内错角、一组同旁内角.
二、探索思考
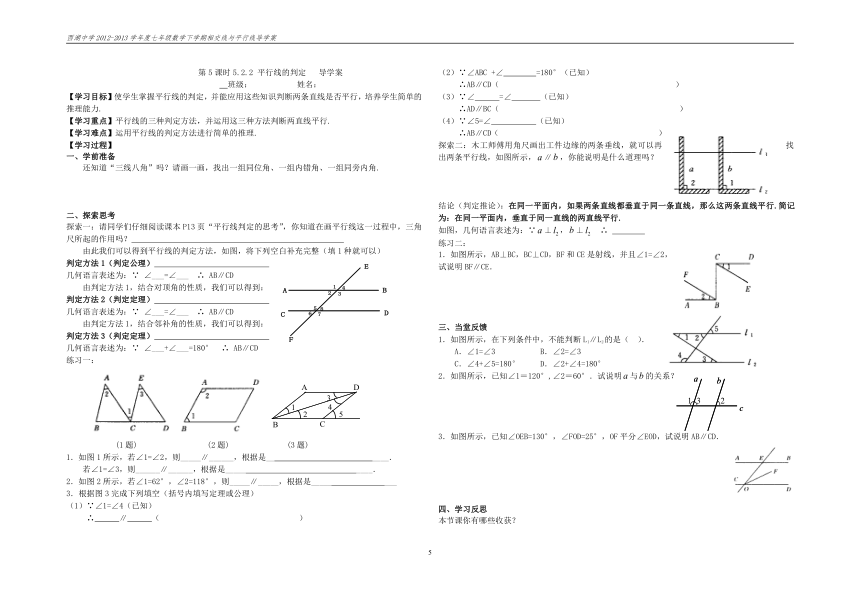
探索一:请同学们仔细阅读课本P13页“平行线判定的思考”,你知道在画平行线这一过程中,三角尺所起的作用吗?
由此我们可以得到平行线的判定方法,如图,将下列空白补充完整(填1种就可以)
判定方法1(判定公理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法1,结合对顶角的性质,我们可以得到:
判定方法2(判定定理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法1,结合邻补角的性质,我们可以得到:
判定方法3(判定定理)
几何语言表述为:∵ ∠___+∠___=180° ∴ AB∥CD
练习一:
(1题) (2题) (3题)
1.如图1所示,若∠1=∠2,则_____∥______,根据是__ ____.
若∠1=∠3,则______∥______,根据是_____ ____.
2.如图2所示,若∠1=62°,∠2=118°,则_____∥_____,根据是_____ ___
3.根据图3完成下列填空(括号内填写定理或公理)
(1)∵∠1=∠4(已知)
∴ ∥ ( )
(2)∵∠ABC +∠ =180°(已知)
∴AB∥CD( )
(3)∵∠ =∠ (已知)
∴AD∥BC( )
(4)∵∠5=∠ (已知)
∴AB∥CD( )
探索二:木工师傅用角尺画出工件边缘的两条垂线,就可以再找出两条平行线,如图所示,∥,你能说明是什么道理吗?
结论(判定推论):在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.简记为:在同一平面内,垂直于同一直线的两直线平行.
如图,几何语言表述为:∵⊥,⊥ ∴
练习二:
1.如图所示,AB⊥BC,BC⊥CD,BF和CE是射线,并且∠1=∠2,
试说明BF∥CE.
三、当堂反馈
1.如图所示,在下列条件中,不能判断L1∥L2的是( ).
A.∠1=∠3 B.∠2=∠3
C.∠4+∠5=180° D.∠2+∠4=180°
2.如图所示,已知∠1=120°,∠2=60°.试说明与的关系?
3.如图所示,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明AB∥CD.
四、学习反思
本节课你有哪些收获?
第6课时5.3.1 平行线的性质 导学案
班级: 姓名:
【学习目标】1使学生掌握平行线的三个性质,并能应用它们进行简单的推理论证;
2使学生经过对比后,理解平行线的性质和判定的区别和联系.
【学习重点】平行线的三个性质及其应用.?
【学习难点】正确理解性质与判定的区别和联系,并正确运用它们去推理证明.
【学习过程】
一、学前准备
通过前面的学习,你知道判定两条直线平行有哪几种方法吗?
⑴平行线的定义:
⑵平行线的传递性:
⑶平行线的判定公理:
⑷平行线的判定定理1:
⑸平行线的判定定理2:
⑹平行线的判定推论:
二、探索思考
探索一:请同学们仔细阅读课本P19页,完成课本上的探究.根据探究内容,我们可以得到平行线的性质,如图,将下列空白补充完整(填1种就可以)
性质1(性质公理)
几何语言表述为:∵ AB∥CD ∴ ∠___=∠___
由性质1,结合对顶角的性质,我们可以得到:
性质2(性质定理)
几何语言表述为:∵ AB∥CD ∴ ∠___=∠___
由性质1,结合邻补角的性质,我们可以得到:
性质3(性质定理)
几何语言表述为:∵ AB∥CD ∴ ∠___+∠___=
练习一:
1. 根据右图将下列几何语言补充完整
(1)∵AD∥ (已知)
∴∠A+∠ABC=180°( )
(2)∵AB∥ (已知)
∴∠4=∠ ( )
∠ABC=∠ ( )
2. 如右图所示,BE平分∠ABC,DE∥ BC,图中相等的角共有( )
A. 3对 B. 4对 C. 5对 D. 6对
3、如图,AB∥CD,∠1=45°,∠D=∠C,求∠D、∠C、∠B的度数.
探索二:用三角尺和直尺画平行线,做成一张5×5个格子的方格纸.观察做出的方格纸的一部分(如图),线段、、…、都与两条平行的横线和垂直吗?
它们的长度相等吗?
像这样,同时垂直于两条平行直线,并且夹在这两条平行线间的线段的长度相等,叫做这两条平行线间的距离,即平行线间的距离处处相等.
练习二:
1.如图所示,已知直线AB∥CD,且被直线EF所截,若∠1=50°,则∠2=____,∠3=______.
(1题) (2题) (3题)
2.如图所示,AB∥CD,AF交CD于E,若∠CEF=60°,则∠A=______.
3.如图所示,已知AB∥CD,BC∥DE,∠1=120°,则∠2=______.
三、当堂反馈
1.如图所示,如果AB∥CD,那么( ).
A.∠1=∠4,∠2=∠5 B.∠2=∠3,∠4=∠5
C.∠1=∠4,∠5=∠7 D.∠2=∠3,∠6=∠8
(1题) (2题) (3题)
2.如图所示,DE∥BC,EF∥AB,则图中和∠BFE互补的角有( ).
A.3个 B.2个 C.5个 D.4个
3.如图所示,已知∠1=72°,∠2=108°,∠3=69°,求∠4的度数.
四、学习反思
本节课你有哪些收获?
第7课时 平行线的判定及性质习题课 导学案
班级: 姓名:
【学习目标】加深对平行线的判定及性质的理解及其应用.
【学习重点】平行线的判定及性质的应用.?
【学习难点】灵活运用平行线的判定及性质去推理证明.
【学习过程】
一、学前准备
通过前面的学习,你知道判定两条直线平行有哪几种方法吗?
⑴平行线的定义:
⑵平行线的传递性:
⑶平行线的判定公理:
⑷平行线的判定定理1:
⑸平行线的判定定理2:
⑹平行线的判定推论:
通过前面的学习,你还知道两条直线平行有哪些性质吗?
⑴根据平行线的定义:
⑵平行线的性质公理:
⑶平行线的性质定理1:
⑷平行线的性质定理2:
⑸平行线间的距离 .
二、探索思考
练习:让我先试试,相信我能行.
1.如图1,若∠1=∠2,那么_____∥______,根据___ __.
若a∥b,那么∠3=_____,根据___ __.
(图1) (图2) (图3) (图4)
2.如图2,∵∠1=∠2,∴_______∥_______,根据___ _____.
∴∠B=______,根据___ _____.
3.如图3,若AB∥CD,那么________=_______;若∠1=∠2,那么_____∥_____;
若BC∥AD,那么_______=_______;若∠A+∠ABC=180°,那么______∥_____
4.如图4,一条公路两次拐弯后,和原来的方向相同,如果第一次拐的角是136°(即∠ABC),那么第二次拐的角(∠BCD)是 度,根据___ .
5.如图,修高速公路需要开山洞,为节省时间,要在山两面A,B
同时开工,在A处测得洞的走向是北偏东76°12′,那么在B处
应按什么方向开口,才能使山洞准确接通,请说明其中的道理.
6.如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过
镜子反射∠1=∠2,∠3=∠4,请你解释为什么开始进入潜望镜的光
线和最后离开潜望镜的光线是平行的.
三、当堂反馈
1.已知如图1,用一吸管吸吮易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹角∠2=_______.
2.已知如图2,边OA,OB均为平面反光镜,∠AOB=40°,在OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB的度数是( ).
A.60° B.80° C.100° D.120°
(图1) (图2) (图3)
3.如图3,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理.
4.如图,直线DE经过点A,DE∥BC,∠B=44°,∠C=85°.⑴求∠DAB的度数;⑵求∠EAC的度数;⑶求∠BAC的度数;⑷通过这道题你能说明为什么三角形的内角和是180°吗?
四、学习反思
本节课你有哪些收获?
第8课时5.3.2命题、定理 导学案
班级: 姓名:
【学习目标】了解命题、定理的概念,能够区分命题的题设和结论.
【学习重点】能够区分命题的题设和结论.?
【学习难点】能够区分命题的题设和结论.
【学习过程】
一、学前准备
歌德是18世纪德国的一位著名文艺大师,一天,他与一位批评家“独路相逢”,这位文艺批评家生性古怪,遇到歌德走来,不仅没有相让,反而卖弄聪明,边走边大声说道:“我从来不给傻子让路!”而对如此的尴尬的局面,歌德笑容可掏,谦恭的闪在一旁,有礼貌地回答道“呵呵,我可恰相反”,结果故作聪明的批评家,反倒自讨没趣.你知道为什么吗?
二、探索思考
探索:在日常生活中,我们会遇到许多类似的情况,需要对一些事情作出判断,例如:
⑴今天是晴天;⑵对顶角相等;⑶如果两条直线都与第三条直线平行,那么这两条直线也互相平行.像这样,判断一件事情的语句,叫做命题.
每个命题都是由_______和______组成.每个命题都可以写成.“如果……,那么……”的形式,用“如果”开始的部份是 ,用“那么”开始的部份是 .
像前面举例中的⑵⑶两个命题,都是正确的,这样的命题叫做真命题,即正确的命题叫做______.
例如:“如果一个数能被2整除,那么这个数能被4整除”,很明显是错误的命题,这样的命题叫做假命题,即错误的命题叫做______.
我们把从长期的实践活动中总结出来的正确命题叫做公理;通过正确的推理得出的真命题叫做定理.
练习:
1.下列语句是命题的个数为( )
①画∠AOB的平分线; ②直角都相等; ③同旁内角互补吗? ④若│a│=3,则a=3.
A.1个 B.2个 C.3个 D.4个
2.下列5个命题,其中真命题的个数为( )
①两个锐角之和一定是钝角; ②直角小于夹角; ③同位角相等,两直线平行;
④内错角互补,两直线平行; ⑤如果a A.1个 B.2个 C.3个 D.4个
3.下列说法正确的是( )
A.互补的两个角是邻补角 B.两直线平行,同旁内角相等
C.“同旁内角互补”不是命题 D.“相等的两个角是对顶角”是假命题
4.“同一平面内,垂直于同一条直线的两条直线互相平行”是 命题,其中,题设
是 ,结论是 ,
5.将下列命题改写成“如果……那么……”的形式.
(1)直角都相等.
(2)末位数是5的整数能被5整除.
(3)三角形的内角和是180°.
(4)平行于同一条直线的两条直线互相平行.
三、当堂反馈
1.下列语句中不是命题的有( )
⑴两点之间,直线最短;⑵不许大声讲话;⑶连接A、B两点;⑷花儿在春天开放.
A.1个 B.2个 C.3个 D.4个
2.下列命题中,正确的是( )
A.在同一平面内,垂直于同一条直线的两条直线平行;
B.相等的角是对顶角;
C.两条直线被第三条直线所截,同位角相等;
D.和为180°的两个角叫做邻补角.
3.下列命题中的条件(题设)是什么?结论是什么?
(1)如果两个角相等,那么它们是对顶角;
(2)如果两条直线都与第三条直线平行,那么这两条直线也平行;
4.将下列命题改写成“如果……那么……”的形式,并判断正误.
(1)对顶角相等;
(2)同位角相等;
(3)同角的补角相等.
四、学习反思
本节课你有哪些收获?
第9课时5.4平移 导学案
班级: 姓名:
【学习目标】1了解平移的概念,知道生活中常见的平移例子;
2掌握平移的规律,会利用平移画图.
【学习重点】平移的规律,画图.?
【学习难点】利用平移的特征画图.
【学习过程】
一、学前准备
生活中有许多美丽的图案,他们都有着共同的特点,请同学们欣赏下面图案.
观察上面图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?请你试一试.
二、探索思考
探究一:请同学们仔细阅读课本P27~28页,你能发现并归纳平移的特征吗?
平移的特征:(1)把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小 ;
(2)新图形中的每一点,都是由原图形中的某一个点移动后得到的,这两个点是 ;
(3)连接各组对应点的线段平行(或在同一条直线上)且 .
即,在平面内,将一个图形沿 移动一定的 ,图形的这种移动,叫做平移变换,简称平移.
注意:图形平移的方向,不一定是水平的.图形经过平移后,_______图形的位置,________图形的形状,________图形的大小.(填“改变”或“不改变”)
练习一:
1.几何图形经过平移,图形中对应点所连的线段平行(或在同一条直线上)且 ,对应线段 且 ,对应角 .
2.平移改变的是图形的( ).
A.位置 B.形状 C.大小 D.位置、形状、大小
3.下列现象中,不属于平移的是( ).
A.滑雪运动员在的平坦雪地上滑行 B.大楼上上下下地迎送来客的电梯
C.钟摆的摆动 D.火车在笔直的铁轨上飞驰而过
4.下列各组图形,可经平移变换由一个图形得到另一个图形的是( ).
探究二:你能按要求将图形平移吗?动手试一试.
如图所示,把△ABC沿AB方向平移,平移的距离为线段a的长.
练习二:
1.如图所示,经过平移,四边形ABCD的顶点A移到点A′,作出平移后的四边形.
三、当堂反馈
1.一个图形先向右平移5个单位,再向左平移7个单位,所得到的图形可以看作是原来位置的图形一次性向_____平移______个单位得到.
2.∠DEF是∠ABC经过平移得到的,∠ABC=60°,则∠DEF=
3.如图,△ABC平移后得到了△A'B'C',其中点C的对应点是点C',已经标明,请你将点B'、点A'在图中标出来,并画出△A'B'C';若AB边上的中点为M,请你再标出点M的对应点M'.
4.已知△ABC、,过点D作△ABC平移后的图形,其中点D与点A对应.
四、学习反思
本节课你有哪些收获?
第10课时 相交线与平行线全章复习 导学案
班级: 姓名:
一、本章知识结构图
二、本章知识梳理
1.邻补角的定义: .
对顶角的定义: .
对顶角的性质: .
2.当两条直线相交所成的四个角中有一个为直角时,叫做这两条直线互相垂直,其中的一条直线叫 ,它们的交点叫 .
如图,用几何语言表示:
方式⑴∵ ∠AOC=90° ∴ AB_____CD,垂足是_____
方式⑵∵ AB⊥CD于O ∴ ∠AOC=______
3.在同一平面内,过一点有且只有_____条直线与已知直线垂直.
注意:垂线是 ,垂线段是一条 ,是图形.点到直线的
距离是 的长度,是一个数量,不能说“垂线段”是距离.
4.识别同位角、内错角、同旁内角的关键是要抓住“三线八角”,
只有“三线”出现且必须是两线被第三线所截才能出现这三类角;
位置1
位置2
结论
∠1和∠5
处于直线c的同侧
处于直线a、b的同一方
这样位置的一对角就称为( )
∠3和∠5
这样位置的一对角就称为( )
∠4和∠5
这样位置的一对角就称为( )
5. 现在所说的两条直线的位置关系,是两条直线在“ ”的前提下提出来的,它们的位置关系只有两种:一是 (有一个公共点),二是 (没有公共点).
6.平行线的定义:在同一平面内, 的两条直线叫做平行线.
平行公理:经过直线外一点, 一条直线与这条直线平行.
平行线的传递性:平行于同一直线的两直线 .
7.两条直线平行的判定方法:⑴平行线的定义,⑵平行线的传递性,
⑶平行线的判定公理:
⑷平行线的判定定理1:
⑸平行线的判定定理2:
⑹平行线的判定推论:
8.两条直线平行的性质:⑴根据平行线的定义
⑵平行线的性质公理:
⑶平行线的性质定理1:
⑷平行线的性质定理2:
⑸平行线间的距离 .
9.命题的定义:判断一件事情的语句,叫做命题.
每个命题都是由_______和______组成.每个命题都可以写成.“如果……,那么……”的形式,用“如果”开始的部份是 ,用“那么”开始的部份是 ,正确的命题叫做______,错误的命题叫做______.从长期的实践活动中总结出来的正确命题叫做 ,通过正确的推理得出的真命题叫做 .
10.平移的特征:(1)把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小 ;(2)新图形中的每一点,都是由原图形中的某一个点移动后得到的,这两个点是 ;(3)连接各组对应的线段 .即,在平面内,将一个图形沿 移动一定的 ,图形的这种移动,叫做平移变换,简称 .图形平移的方向,不一定是水平的.图形经过平移后,_______图形的位置,________图形的形状,________图形的大小.(填“改变”或“不改变”)
三、巩固练习
1.如图1,直线a,b相交于点O,若∠1=40°,则∠2等于_______.
图1 图2 图3 图4 图5
2.如图2,直线a∥b,∠1=123°30′,则∠2=______.
3.如图3,已知a∥b,∠1=70°,∠2=40°,则∠3=_____.
4.如图4,AB∥CD,∠E=40°,∠C=65°,则∠EAB的度数为( )
A.65° B.75° C.105° D.115°
5.如图5,直线L1与L2相交于点O,OM⊥L1,若α=44°,则β为( )
A.56° B.46° C.45° D.44°
6.如图6,AB∥CD,直线PQ分别交AB,CD于点E,F,FG是∠EFD的平分线,交AB于点G,若∠FEG=40°,那么∠FGB等于( )
A.80° B.100° C.110° D.120°
7.如图7,已知∠1=∠2=∠3=55°,则∠4的度数为( )
A.55° B.75° C.105° D.125°
第11课时 相交线与平行线 训练题
班级 姓名
【学习目标】理解相交线与平行线的意义, 掌握 命题的概念及结构,并会判断命题及真假
【学习重点】理解“三线八角” 掌握平行线的判定方法及性质。?
【学习难点】平行线的判定及性质的反复交错使用
A卷(基础知识部分,50分)
一、精心选一选(每题2分,共10分)
1.直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;(2)如果a∥b,b∥c,那么a∥c;(3)如果a∥b,b⊥c,那么a⊥c;(4)如果a与b相交,b与c相交,那么a 与c相交;在上述四种说法中,正确的有 ( )A.1个 B.2个 C.3个 D.4个
2.三条直线两两相交于同一点时,对顶角有m对,交于不同三点时,对顶角有n对,则m与n的关系是( ) A.m = n B.m>n C.m<n D.m + n = 10
3.A、B、C是直线l上的三点,P是直线l外一点.若PA=5cm、PB=6cm、PC=8cm.由此可知,点P到直线l的距离是 ( )A.5cm B.不小于5cm C.不大于5cm D.在6cm与8cm之间
4.平移后的图形与原图形对应点的连线段( )
A.相等 B.平行 C.平行且相等 D.平行且相等或在同一条直线上
5.如图,如果AC⊥BC,CD⊥AB,∠1=∠2,那么下列结论中正确的个数是( )
(1)∠1=∠B;(2)∠A=∠3;(3)AC∥DE;(4)∠2与∠B互余;(5)∠2=∠A;(6)A、C两点之间的距离就是线段AC的长; A.3个 B.4个 C.5个 D.6个
二、细心填一填(每题3分,共15分)
6.如图,AB∥CD,∠B=680,∠E=200,则∠D的度数为___________.
7.如图,由A测B的方向是_________________
8.如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是___________
9.如图,已知AB∥CD,∠1=30°,∠2=90°,则∠3等于_____________
10.把命题“等角的补角相等”改写成“如果……,那么……”的形式___________________.
三、耐心解一解(第11~13题各6分,第14题7分,共25分)
11.如图,EF∥AD,∠1 =∠2,∠BAC = 70°.将求∠AGD的过程填写完整.
因为EF∥AD,所以 ∠2 =______.又因为 ∠1 = ∠2,所以 ∠1 = ∠3. 所以AB∥____.所以∠BAC +______= 180°.又因为∠BAC = 70°,所以∠AGD =______.
12.已知三角形ABC、点D为点B平移后的对应点,过点D作三角形ABC平移后的图形
13.如图,已知直线AB、CD被直线EF所截,交AB,CD于点M、N,NH是一条射线,图中共有多少对同位角?多少对内错角?多少对同旁内角?分别指出这些角.
14.如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
B卷(激活训练部分,50分)
一、精心选一选(每题2分,共10分)
15.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是 ( )
A.第一次向右拐40°,第二次左拐140° B. 第一次向左拐40°,第二次右拐40°
C.第一次向左拐40°,第二次左拐140° D. 第一次向右拐40°,第二次右拐40°
16.将已知点P平移5cm后得到点P’,满足条件的点P’构成的图形是 ( )
A.一个点 B.两个点 C.一条5cm长的线段PP’ D.一个半径5cm的圆
17.如图,在5×5方格纸中将左图中的图形N平移后的位置右图中所示,那么正确的平移方法是( ).
A.先向下移动1格,再向左移动1格 B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格 D.先向下移动2格,再向左移动2格
18.如图,直线a∥b,点B在直线b上,且AB⊥BC ,∠1=55 o ,则∠2 的度数为( )
A . 35 o B . 45 o C . 55 o D . 125o
18 1917
19.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
二、细心填一填(每题3分,共15分)
20.把一副三角板按如图方式放置,则两条斜边所形成的钝角_______度.
20 21 22
21.如图,∠ABC和∠ACB的平分线BO与CO相交于点O,EF过点O,且EF∥BC,若∠BOC=130°,∠ABC∶∠ACB=3∶2,则∠AEF=_________,∠EFC=_________.
22.如图,直线AB∥CD,直线EF交AB于G,交CD于F,直线EH交AB于H.若∠1=45°,∠2=60°,则∠E的度数为________ 度.
23.如图,直线与直线互相平行,则的值是____________
23 24
24.如图,AB∥CD,∠A=120°,∠1=72°,则∠D的度数为__________.
三、耐心解一解(第25~27题各6分,第28题7分,共25分)
25.直线AB、CD相交于点O,OE⊥AB于O,且∠DOE=4∠COE,求∠AOD的度数.
26.如图,直线DE过点A,F是BA延长线上一点,具备什么条件时,可以判定DE∥BC?为什么?
27.已知:如图,AB∥CD,∠B=∠D. 求证:∠1=∠2
28.如图,已知∠1=∠2,再添上什么条件可使AB∥CD成立?并就你添上的条件证明AB∥CD .
第12课时 相交线与平行线 训练题
班级 姓名
【学习目标】理解相交线与平行线的意义, 掌握有关计算常用方法.
【学习重点】理解“三线八角” 掌握平行线的判定方法及性质。?
【学习难点】平行线的判定及性质的反复交错使用
一、填空题(每空2′,共2′×9)
1、如果∠A=35°18′,那么∠A的余角等于_____;
2、如图①,直线a、b被直线c所截(即直线c与直线a、b都相交),
且a∥b,若∠1=118°,则∠2的度数=_____;
3、一个角的补角比这个角的余角大___度;
4、推理填空,如图③∵∠B=___; ∴AB∥CD(____________);
∵∠DGF=___; ∴CD∥EF(____________);
∵AB∥EF; ∴∠B+___=180°(___________);
二、选择题(4′×2)
5、如果一个角的补角是150°,那么这个角的余角的度数是( )
A 30° B 60° C 90° D 120°
6、如图②,已知直线a、b被直线c所截,a∥b,∠1=50°,则∠2=( ) A 50° B 130° C 40° D 60°
下列各题期望你仔细阅读题目、明确已知与所需解决的问题,认真观察、思考、推断;其中有的知识是上学期学过的,你可能忘了,你重新复习这些知识好吗?
三、解答下列各题(60′)
7、(8′)如图④,在四边形ABCD中,已知AB∥CD,∠B=60°,你能求出哪些角的度数?
为什么?你能求出∠A的度数吗?
?
?
?
?
?8、(8′)如图⑤,在四边形ABCD中,已知∠B=60°,∠C=120°,由这些条件你能判断哪两条直线平行?说说你的理由。
?
?
?
?
9、(10′)如图⑥,已知∠1=30°,∠B=60°,AB⊥AC,
⑴∠DAB+∠B=_____;
⑵AB与CD平行吗?AD与BC平行吗?
10、(10′)如图⑦,∠1=∠2,能判断AB∥DF吗?为什么?若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
?
?
?11、(12′)如图⑧,BC∥DE,小颖用量角器分别画出∠ABC、∠ADE的角平分线BG、DH,想一想,小颖所画的这两条射线BG和DH会平行吗?为什么?(请你先用量角器画出这两条角平分线)
?
?
12、(12′)如图⑨,左图是一个三角形,已知∠ACB=90°,
那么∠A的余角是哪个角呢?答:___;
小明用三角尺在这个三角形中画了一条高CD(点D是垂足),得到右图?
?⑴请你帮小明画出这条高;
⑵在右图中,小明通过仔细观察、认真思考,找出了
三对余角,你能帮小明把它们写出来吗?
答:①_________;②_________;
③_________。
⑶∠ACB、∠ADC、∠CDB都是直角,所以∠ACB=∠ADC=∠CDB,小明还发现了另外两对相等的角,请你也仔细地观察、认真地思考分析,试一试,能发现吗?把它们写出来,并请说明理由。
?
?四、(6′)推理分析
13、一个小朋友的颜料盒中有6种不同颜色的彩笔,它们的颜色顺次是yellow,red,blue,tan,pink,green,并且名称都写在彩笔上。他用了其中1支彩笔给某个图形涂颜色,他用了哪支彩笔呢?这里有三个条件:第一,它的字母至少在3个以上,6个以下;第二,这个彩笔不在red旁边;第三,这支彩笔不是最后一个。 请你猜出是哪一支,并简说你的理由。
?
??五、(8′)找规律(先动手画画,然后思考分析从中找出规律)
14、平面内有若干条直线,当下列情形时,可将平面最多分成几部分:
⑴有一条直线时,最多分成 2 部分;
⑵有二条直线时,最多分成 2+2=4 部分;
⑶有三条直线时,最多分成________部分;
(n)有n条直线时,最多分成________部分。
?15.如图,在四边形ABCD中,∠A=104°-∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F,能辨认∠1=∠2吗?试说明理由.
第13课时 相交线与平行线 训练题
班级 姓名
【学习目标】理解相交线与平行线的意义, 掌握有关计算常用方法.
【学习重点】理解“三线八角” 掌握平行线的判定方法及性质。?
【学习难点】平行线的判定及性质的反复交错使用
一、选择题(选择填空2分一题)
1、如果一个角的补角是150°,那么这个角的度数是( )
A. 30° B. 60° C.90° D.120°
2、如图,已知直线a、b被直线c所截,a∥b,∠1=130°,则 ∠2=( )
A. 130° B. 50° C.40° D.60°
3、下列说法错误的是( )
A.内错角相等,两直线平行. B.两直线平行,同旁内角互补.
C.相等的角是对顶角. D.等角的补角相等.
4、下列图中∠1和∠2是同位角的是( )
A. ⑴、⑵、⑶, B. ⑵、⑶、⑷, C. ⑶、⑷、⑸, D. ⑴、⑵、⑸
5、已知:如图, ∠1=∠2 , 则有( )
A.AB∥CD B.AE∥DF C. AB∥CD 且AE∥DF D.以上都不对
6、如图,直线AB与CD交于点O,OE⊥AB于O,图∠1与∠2的关系是( )
A.对顶角 B.互余 C.互补 D相等
7、如图,DH∥EG∥BC,且DC∥EF,那么图中和∠1相等的角的个数是( )
A.2, B. 4, C. 5, D. 6
8、如图,AB//CD,BC//DE,则∠B+∠D的值为( )
A.90° B.150° C.180° D. 以上都不对
9、如图,直线AB与CD相交于点O,OB平分∠DOE.若∠DOE=60 o,
则∠AOE的度数是( ) A.90° B.150° C.180° D. 不能确定
10、一束光线垂直照射在水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为( )
A.45o B.60o C.75o D.80o
11、(2009临沂)下列图形中,由,能得到的是( )
12、(2009年遂宁)如图,已知∠1=∠2,∠3=80O,则∠4=( )
A.80O B. 70O C. 60O D. 50O
13、(2009年娄底)如图1,已知AC∥ED,∠C=26°,∠CBE=37°,则∠BED的度数是 ( )?
A.63° B.83° C.73° D.53°?
14、(2009年桂林市、百色市)如图,在所标识的角中,同位角是( ).
A.和 B.和 C.和 D.和
15、(2009年肇庆市)如图,中,,DE 过点C,且,若,则∠B的度数( ) A.35° B.45 C.55° D.65°
16、(2009年崇左)如图,把矩形沿对折后使两部分重合,若,则=( ) A.110° B.115° C.120° D.130°
二、填空 1、用尺规作图时,用 画直线、射线和直线,用 画弧或圆。
2、黎老师家在小星家的北偏东 68 度,则小星家在黎老师家的南偏西 度 。
3、如图①,如果∠ = ∠ ,可得AD∥BC,你的根据是 。
4、如图②,∠1 = 82o,∠2 = 98o,∠3 = 80o,则∠4 = 度。
5、如图③,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,
∠FOD = 28o,则∠BOE = 度,∠AOG = 度。
6、一个角与它的补角之差是20o,则这个角的度数是 度。
7、如图④,AB∥CD,∠BAE = 120o,∠DCE = 30o,则∠AEC = 度。
8、如图⑤,OA⊥OB,OC⊥OD,O是垂足,∠BOC=55o,那么∠AOD= .
9、如图⑥中∠DAB和∠B是直线DE和BC被直线 所截而成的,称它们为 角。
10、把一张长方形纸条按图⑤中,那样折叠后,若得到∠AOB′= 70o,则∠B′OG = 。
三、解答题:(6分一题)
1、完成推理填空:如图:已知∠A=∠F,∠C=∠D,求证:BD∥CE 。
请你认真完成下面的填空。
证明:∵∠A=∠F ( 已知 )∴AC∥DF ( ___________ )
∴∠D=∠ ( _____________ )
又∵∠C=∠D ( 已知 ),∴∠1=∠C ( 等量代换 )
∴BD∥CE( )。
2、如图:已知AB∥A′B′,BC∥B′C′,那么∠B与∠B′有何关系?为什么?
3、如图:a∥b,∠1=122°,∠3=50°,求∠2和∠4的度数 。
4、如图 ,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E = 140o,
求∠BFD的度数?
5. 如图所示,已知∠E=∠DAB,∠F=∠C,请你简要说明
AB与CD是否平行。
6. 如图所示,已知∠DAC=∠ACB,∠D=62°,求∠BCD的度数。
7、(2009年淄博市)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37o,求∠D的度数.
第1课时:5.1.1 相交线 导学案
班级: 姓名:
【学习目标】了解邻补角、对顶角, 能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些问题.
【学习重点】邻补角、对顶角的概念,对顶角性质与应用.?
【学习难点】理解对顶角相等的性质.
【学习过程】
一、学前准备
各小组对七年级上学过的直线、射线、线段、角做总结.每人写一个总结小报告,并编写两道与它们相关的题目,在小组交流,并推出小组最好的两道题在班级汇报.
二、探索思考
探索一:完成课本P2页的探究,填在课本上.
你能归纳出“邻补角”的定义吗? .
“对顶角”的定义呢? .
练习一:
1.如图1所示,直线AB和CD相交于点O,OE是一条射线.
(1)写出∠AOC的邻补角:____ _ ___ __;
(2)写出∠COE的邻补角: __;
(3)写出∠BOC的邻补角:____ _ ___ __;
(4)写出∠BOD的对顶角:____ _.
2.如图所示,∠1与∠2是对顶角的是( )
探索二:任意画一对对顶角,量一量,算一算,它们相等吗?如果相等,请说明理由.
请归纳“对顶角的性质”: .
练习二:
1.如图,直线a,b相交,∠1=40°,则∠2=_______∠3=_______∠4=_______
2.如图直线AB、CD、EF相交于点O,∠BOE的对顶角是______,∠COF 的邻补角是____,若∠AOE=30°,那么∠BOE=_______,∠BOF=_______
3.如图,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠EOF=_____.
三、当堂反馈
1.若两个角互为邻补角,则它们的角平分线所夹的角为 度.
2.如图所示,直线a,b,c两两相交,∠1=60°,∠2=∠4,求∠3、∠5的度数.
3.如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,你能说出所量的角是多少度吗?你的根据是什么?
4.探索规律:
(1)两条直线交于一点,有 对对顶角;
(2)三条直线交于一点,有 对对顶角;
(3)四条直线交于一点,有 对对顶角;
(4)n条直线交于一点,有 对对顶角.
四、学习反思
本节课你有哪些收获?
第2课时 5.1.2 垂线 导学案
班级: 姓名:
【学习目标】1了解垂线、点到直线的距离的意义,理解垂线和垂线段的性质;
2会用三角板过一点画已知直线的垂线,并会度量点到直线的距离.
【学习重点】垂线的意义、性质和画法,垂线段性质及其简单应用.?
【学习难点】垂线的画法以及对点到直线的距离的概念的理解.
【学习过程】
一、学前准备
在学习对顶角知识的时候,我们认识了“两线四角”,及两条直线相交于一点,得到四个角,这四个角里面,有两对对顶角,它们分别对应相等,如图,可以说成“直线AB与CD相交于点O”.
我们如果把直线CD绕点O旋转,无论是按照顺时针方向转,还是按照逆时针方向转,∠BOD的大小都将发生变化.
当两条直线相交所成的四个角中有一个为直角时,叫做这两条直线互相垂直,其中的一条直线叫垂线,它们的交点叫垂足.如图
用几何语言表示:
方式⑴∵ ∠AOC=90° ∴ AB_____CD,垂足是_____
方式⑵∵ AB⊥CD于O ∴ ∠AOC=______
二、探索思考
探索一:请你认真画一画,看看有什么收获.
⑴如图1,利用三角尺或量角器画已知直线的垂线,这样的垂线能画__________条;
⑵如图2,经过直线上一点A画的垂线,这样的垂线能画_____条;
⑶如图3,经过直线外一点B画的垂线,这样的垂线能画_____条;
(图1) (图2) (图3a) (图3b)
经过探索,我们可以发现:在同一平面内,过一点有且只有_____条直线与已知直线垂直.
练习一:
1.如图所示,OA⊥OB,OC是一条射线,若∠AOC=120°,
求∠BOC度数
2.如图所示,直线AB⊥CD于点O,直线EF经过点O,
若∠1=26°,求∠2的度数.
3.如图所示,直线AB,CD相交于点O,P是CD上一点.
(1)过点P画AB的垂线PE,垂足为E.
(2)过点P画CD的垂线,与AB相交于F点.
(3)比较线段PE,PF,PO三者的大小关系
探索二:仔细观察测量比较上题中点P分别到直线AB上三点E、F、O的距离,你还有什么收获?请将你的收获记录下来:_______________________________________________
简单说成: .还有,直线外一点到这条直线的垂线段的 叫做点到直线的距离.注意:垂线是 ,垂线段是一条 ,点到直线的距离是一个数量,不能说“垂线段”是距离.
练习二:
1.在下列语句中,正确的是( ).
A.在同一平面内,一条直线只有一条垂线
B.在同一平面内,过直线上一点的直线只有一条
C.在同一平面内,过直线上一点且垂直于这条直线的直线有且只有一条
D.在同一平面内,垂线段就是点到直线的距离
2.如图所示,AC⊥BC,CD⊥AB于D,AC=5cm,BC=12cm,AB=13cm,则点B到AC的距离是________,点A到BC的距离是_______,点C到AB的距离是_______,AC>CD的依据是_________.
三、当堂反馈
1.如图所示AB,CD相交于点O,EO⊥AB于O,FO⊥CD于O,∠EOD与∠FOB的大小关系是( )
A.∠EOD比∠FOB大 B.∠EOD比∠FOB小
C.∠EOD与∠FOB相等 D.∠EOD与∠FOB大小关系不确定
2.如图,一辆汽车在直线形的公路AB上由A向B行驶,C,D是分别位于公路AB两侧的加油站.设汽车行驶到公路AB上点M的位置时,距离加油站C最近;行驶到点N的位置时,距离加油站D最近,请在图中的公路上分别画出点M,N的位置并说明理由.
3.如图,AOB为直线,∠AOD:∠DOB=3:1,OD平分∠COB. (1)求∠AOC的度数;(2)判断AB与OC的位置关系.
四、学习反思
本节课你有哪些收获?
第3课时5.1.3 同位角、内错角、同旁内角 导学案
班级: 姓名:
【学习目标】1使学生理解三线八角的意义,并能从复杂图形中识别它们;
2通过三线八角的特点的分析,培养学生抽象概括问题的能力.
【学习重点】三线八角的意义,以及如何在各种变式的图形中找出这三类角.?
【学习难点】能准确在各种变式的图形中找出这三类角.
【学习过程】
一、学前准备
在前面我们学习了两条直线相交于一点,得到四个角,即“两线四角”,这四个角里面,有 对对顶角,有 对邻补角.如果是一条直线分别与两条直线相交,结果又会怎样呢?
二、探索思考
探索:如图,直线c分别与直线a、b相交(也可以说两条
直线a、b被第三条直线c所截),得到8个角,通常称为
“三线八角”,那么这8个角之间有哪些关系呢?
观察填表: 表一
位置1
位置2
结论
∠1和∠5
处于直线c的同侧
处于直线a、b的同一方
这样位置的一对角就称为同位角
∠2和∠8
处于直线c的( )侧
这样位置的一对角就称为( )
∠3和∠6
处于直线a、b的( )方
这样位置的一对角就称为( )
∠1和∠5
这样位置的一对角就称为( )
表二
位置1
位置2
结论
∠4和∠8
处于直线c的两侧
处于直线a、b之间
这样位置的一对角就称为内错角
∠3和∠5
这样位置的一对角就称为( )
表三
位置1
位置2
结论
∠3和∠8
处于直线c的( )侧
处于直线a、b( )
这样位置的一对角就称为同旁内角
∠4和∠5
这样位置的一对角就称为( )
练习:
1.如图1所示,∠1与∠2是__ _角,∠2与∠4是_ 角,∠2与∠3是__ _角.
(图1) (图2) (图3)
2.如图2所示,∠1与∠2是___ _角,是直线______和直线_______被直线_______所截而形成的,∠1与∠3是___ __角,是直线________和直线______被直线________所截而形成的.
3.如图3所示,∠B同旁内角有哪些?
三、当堂反馈
1.如图,(1)直线AD、BC被直线AC所截,找出图中由AD、BC被直线AC所截而成的内错角是_________和__________
(2)∠3和∠4是直线_________和_________被_________所截,构成内错角.
2.已知∠1与∠2是同旁内角,且∠1=60°,则∠2为( )
A. 60° B. 120° C. 60°或120° D.无法确定
3.如图,判断正误
①∠1和∠4是同位角;( )
②∠1和∠5是同位角;( )
③∠2和∠7是内错角;( )
④∠1和∠4是同旁内角;( )
4.如图,直线DE、BC被直线AB所截.
⑴∠1与∠2、∠1与∠3、∠1与∠4各是什么角?
⑵如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
四、学习反思
本节课你有哪些收获?
第4课时5.2.1 平行线 导学案
班级: 姓名:
【学习目标】1使学生知道平行线的概念,掌握平行公理;
2了解平行线具有传递性,能够画出已知直线的平行线.
【学习重点】平行线的概念和平行公理,利用直尺和三角板画已知直线的平行线.?
【学习难点】用几何语言描述画图过程,根据几何语言画出图形.
【学习过程】
一、学前准备
在上学期我们学过点和直线的位置关系,同学们还记得点和直线有几种位置关系吗?请画出来,并尝试用几何语言来表示.
二、探索思考
探索一:我们知道,火车行驶的两条笔直的铁轨、人行道上的斑马线等都给我们平行的形象.一般地,在同一平面内,不相交的两条直线叫做平行线.如图,记作“∥”或“AB∥CD”,读作“直线平行于直线”.请同学们思考一下:在同一平面内,两条不重合的直线有几种位置关系?动手画一画,并尝试用几何语言来表示..
练习一:
1.下列说法中,正确的是( ).
A.两直线不相交则平行 B.两直线不平行则相交
C.若两线段平行,那么它们不相交 D.两条线段不相交,那么它们平行
2.在同一平面内,有三条直线,其中只有两条是平行的,那么交点有( ).
A.0个 B.1个 C.2个 D.3个
探索二:请同学们仔细阅读课本P13页“平行线的讨论”,认真思考.通过观察和画图,可以体验一个基本事实(平行公理):经过直线外一点, 一条直线与这条直线平行.
同样,我们还有(平行线的传递性):如果两条直线都与第三条直线平行,那么这两条直线也互相平行.简单的说就是:平行于同一直线的两直线平行.
用几何语言可表示为:如果∥,∥,那么 .
练习二:
1.如图1所示,与AB平行的棱有_______条,与AA′平行的棱有_____条.
2.如图2所示,按要求画平行线.
(1)过P点画AB的平行线EF;(2)过P点画CD的平行线MN.
3.如图3所示,点A,B分别在直线,上,(1)过点A画到的垂线段;(2)过点B画直线∥.
(图1) (图2) (图3)
4.下列说法中,错误的有( ).
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,那么a∥c;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂线三种
A.3个 B.2个 C.1个 D.0个
三、当堂反馈
1.在同一平面内,一条直线和两条平行线中一条直线相交,那么这条直线与平行线中的另一边必__________.
2.同一平面内,两条相交直线不可能与第三条直线都平行,这是因为________________.
3.判断题
(1)不相交的两条直线叫做平行线.( )
(2)在同一平面内,不相交的两条射线是平行线.( )
(3)如果一条直线与两条平行线中的一条平行, 那么它与另一条也互相平行.( )
4.读下列语句,并画出图形:
⑴点P是直线AB外一点,直线CD经过点P,且与直线AB平行,直线EF也经过点P且与直线AB垂直.
⑵直线AB,CD是相交直线,点P是直线AB,CD外一点,直线EF经过点P且与直线AB平行,与直线CD相交于E.
四、学习反思
本节课你有哪些收获?
第5课时5.2.2 平行线的判定 导学案
班级: 姓名:
【学习目标】使学生掌握平行线的判定,并能应用这些知识判断两条直线是否平行,培养学生简单的推理能力.
【学习重点】平行线的三种判定方法,并运用这三种方法判断两直线平行.?
【学习难点】运用平行线的判定方法进行简单的推理.
【学习过程】
一、学前准备
还知道“三线八角”吗?请画一画,找出一组同位角、一组内错角、一组同旁内角.
二、探索思考
探索一:请同学们仔细阅读课本P13页“平行线判定的思考”,你知道在画平行线这一过程中,三角尺所起的作用吗?
由此我们可以得到平行线的判定方法,如图,将下列空白补充完整(填1种就可以)
判定方法1(判定公理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法1,结合对顶角的性质,我们可以得到:
判定方法2(判定定理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法1,结合邻补角的性质,我们可以得到:
判定方法3(判定定理)
几何语言表述为:∵ ∠___+∠___=180° ∴ AB∥CD
练习一:
(1题) (2题) (3题)
1.如图1所示,若∠1=∠2,则_____∥______,根据是__ ____.
若∠1=∠3,则______∥______,根据是_____ ____.
2.如图2所示,若∠1=62°,∠2=118°,则_____∥_____,根据是_____ ___
3.根据图3完成下列填空(括号内填写定理或公理)
(1)∵∠1=∠4(已知)
∴ ∥ ( )
(2)∵∠ABC +∠ =180°(已知)
∴AB∥CD( )
(3)∵∠ =∠ (已知)
∴AD∥BC( )
(4)∵∠5=∠ (已知)
∴AB∥CD( )
探索二:木工师傅用角尺画出工件边缘的两条垂线,就可以再找出两条平行线,如图所示,∥,你能说明是什么道理吗?
结论(判定推论):在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.简记为:在同一平面内,垂直于同一直线的两直线平行.
如图,几何语言表述为:∵⊥,⊥ ∴
练习二:
1.如图所示,AB⊥BC,BC⊥CD,BF和CE是射线,并且∠1=∠2,
试说明BF∥CE.
三、当堂反馈
1.如图所示,在下列条件中,不能判断L1∥L2的是( ).
A.∠1=∠3 B.∠2=∠3
C.∠4+∠5=180° D.∠2+∠4=180°
2.如图所示,已知∠1=120°,∠2=60°.试说明与的关系?
3.如图所示,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD,试说明AB∥CD.
四、学习反思
本节课你有哪些收获?
第6课时5.3.1 平行线的性质 导学案
班级: 姓名:
【学习目标】1使学生掌握平行线的三个性质,并能应用它们进行简单的推理论证;
2使学生经过对比后,理解平行线的性质和判定的区别和联系.
【学习重点】平行线的三个性质及其应用.?
【学习难点】正确理解性质与判定的区别和联系,并正确运用它们去推理证明.
【学习过程】
一、学前准备
通过前面的学习,你知道判定两条直线平行有哪几种方法吗?
⑴平行线的定义:
⑵平行线的传递性:
⑶平行线的判定公理:
⑷平行线的判定定理1:
⑸平行线的判定定理2:
⑹平行线的判定推论:
二、探索思考
探索一:请同学们仔细阅读课本P19页,完成课本上的探究.根据探究内容,我们可以得到平行线的性质,如图,将下列空白补充完整(填1种就可以)
性质1(性质公理)
几何语言表述为:∵ AB∥CD ∴ ∠___=∠___
由性质1,结合对顶角的性质,我们可以得到:
性质2(性质定理)
几何语言表述为:∵ AB∥CD ∴ ∠___=∠___
由性质1,结合邻补角的性质,我们可以得到:
性质3(性质定理)
几何语言表述为:∵ AB∥CD ∴ ∠___+∠___=
练习一:
1. 根据右图将下列几何语言补充完整
(1)∵AD∥ (已知)
∴∠A+∠ABC=180°( )
(2)∵AB∥ (已知)
∴∠4=∠ ( )
∠ABC=∠ ( )
2. 如右图所示,BE平分∠ABC,DE∥ BC,图中相等的角共有( )
A. 3对 B. 4对 C. 5对 D. 6对
3、如图,AB∥CD,∠1=45°,∠D=∠C,求∠D、∠C、∠B的度数.
探索二:用三角尺和直尺画平行线,做成一张5×5个格子的方格纸.观察做出的方格纸的一部分(如图),线段、、…、都与两条平行的横线和垂直吗?
它们的长度相等吗?
像这样,同时垂直于两条平行直线,并且夹在这两条平行线间的线段的长度相等,叫做这两条平行线间的距离,即平行线间的距离处处相等.
练习二:
1.如图所示,已知直线AB∥CD,且被直线EF所截,若∠1=50°,则∠2=____,∠3=______.
(1题) (2题) (3题)
2.如图所示,AB∥CD,AF交CD于E,若∠CEF=60°,则∠A=______.
3.如图所示,已知AB∥CD,BC∥DE,∠1=120°,则∠2=______.
三、当堂反馈
1.如图所示,如果AB∥CD,那么( ).
A.∠1=∠4,∠2=∠5 B.∠2=∠3,∠4=∠5
C.∠1=∠4,∠5=∠7 D.∠2=∠3,∠6=∠8
(1题) (2题) (3题)
2.如图所示,DE∥BC,EF∥AB,则图中和∠BFE互补的角有( ).
A.3个 B.2个 C.5个 D.4个
3.如图所示,已知∠1=72°,∠2=108°,∠3=69°,求∠4的度数.
四、学习反思
本节课你有哪些收获?
第7课时 平行线的判定及性质习题课 导学案
班级: 姓名:
【学习目标】加深对平行线的判定及性质的理解及其应用.
【学习重点】平行线的判定及性质的应用.?
【学习难点】灵活运用平行线的判定及性质去推理证明.
【学习过程】
一、学前准备
通过前面的学习,你知道判定两条直线平行有哪几种方法吗?
⑴平行线的定义:
⑵平行线的传递性:
⑶平行线的判定公理:
⑷平行线的判定定理1:
⑸平行线的判定定理2:
⑹平行线的判定推论:
通过前面的学习,你还知道两条直线平行有哪些性质吗?
⑴根据平行线的定义:
⑵平行线的性质公理:
⑶平行线的性质定理1:
⑷平行线的性质定理2:
⑸平行线间的距离 .
二、探索思考
练习:让我先试试,相信我能行.
1.如图1,若∠1=∠2,那么_____∥______,根据___ __.
若a∥b,那么∠3=_____,根据___ __.
(图1) (图2) (图3) (图4)
2.如图2,∵∠1=∠2,∴_______∥_______,根据___ _____.
∴∠B=______,根据___ _____.
3.如图3,若AB∥CD,那么________=_______;若∠1=∠2,那么_____∥_____;
若BC∥AD,那么_______=_______;若∠A+∠ABC=180°,那么______∥_____
4.如图4,一条公路两次拐弯后,和原来的方向相同,如果第一次拐的角是136°(即∠ABC),那么第二次拐的角(∠BCD)是 度,根据___ .
5.如图,修高速公路需要开山洞,为节省时间,要在山两面A,B
同时开工,在A处测得洞的走向是北偏东76°12′,那么在B处
应按什么方向开口,才能使山洞准确接通,请说明其中的道理.
6.如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过
镜子反射∠1=∠2,∠3=∠4,请你解释为什么开始进入潜望镜的光
线和最后离开潜望镜的光线是平行的.
三、当堂反馈
1.已知如图1,用一吸管吸吮易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹角∠2=_______.
2.已知如图2,边OA,OB均为平面反光镜,∠AOB=40°,在OB上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB的度数是( ).
A.60° B.80° C.100° D.120°
(图1) (图2) (图3)
3.如图3,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理.
4.如图,直线DE经过点A,DE∥BC,∠B=44°,∠C=85°.⑴求∠DAB的度数;⑵求∠EAC的度数;⑶求∠BAC的度数;⑷通过这道题你能说明为什么三角形的内角和是180°吗?
四、学习反思
本节课你有哪些收获?
第8课时5.3.2命题、定理 导学案
班级: 姓名:
【学习目标】了解命题、定理的概念,能够区分命题的题设和结论.
【学习重点】能够区分命题的题设和结论.?
【学习难点】能够区分命题的题设和结论.
【学习过程】
一、学前准备
歌德是18世纪德国的一位著名文艺大师,一天,他与一位批评家“独路相逢”,这位文艺批评家生性古怪,遇到歌德走来,不仅没有相让,反而卖弄聪明,边走边大声说道:“我从来不给傻子让路!”而对如此的尴尬的局面,歌德笑容可掏,谦恭的闪在一旁,有礼貌地回答道“呵呵,我可恰相反”,结果故作聪明的批评家,反倒自讨没趣.你知道为什么吗?
二、探索思考
探索:在日常生活中,我们会遇到许多类似的情况,需要对一些事情作出判断,例如:
⑴今天是晴天;⑵对顶角相等;⑶如果两条直线都与第三条直线平行,那么这两条直线也互相平行.像这样,判断一件事情的语句,叫做命题.
每个命题都是由_______和______组成.每个命题都可以写成.“如果……,那么……”的形式,用“如果”开始的部份是 ,用“那么”开始的部份是 .
像前面举例中的⑵⑶两个命题,都是正确的,这样的命题叫做真命题,即正确的命题叫做______.
例如:“如果一个数能被2整除,那么这个数能被4整除”,很明显是错误的命题,这样的命题叫做假命题,即错误的命题叫做______.
我们把从长期的实践活动中总结出来的正确命题叫做公理;通过正确的推理得出的真命题叫做定理.
练习:
1.下列语句是命题的个数为( )
①画∠AOB的平分线; ②直角都相等; ③同旁内角互补吗? ④若│a│=3,则a=3.
A.1个 B.2个 C.3个 D.4个
2.下列5个命题,其中真命题的个数为( )
①两个锐角之和一定是钝角; ②直角小于夹角; ③同位角相等,两直线平行;
④内错角互补,两直线平行; ⑤如果a
3.下列说法正确的是( )
A.互补的两个角是邻补角 B.两直线平行,同旁内角相等
C.“同旁内角互补”不是命题 D.“相等的两个角是对顶角”是假命题
4.“同一平面内,垂直于同一条直线的两条直线互相平行”是 命题,其中,题设
是 ,结论是 ,
5.将下列命题改写成“如果……那么……”的形式.
(1)直角都相等.
(2)末位数是5的整数能被5整除.
(3)三角形的内角和是180°.
(4)平行于同一条直线的两条直线互相平行.
三、当堂反馈
1.下列语句中不是命题的有( )
⑴两点之间,直线最短;⑵不许大声讲话;⑶连接A、B两点;⑷花儿在春天开放.
A.1个 B.2个 C.3个 D.4个
2.下列命题中,正确的是( )
A.在同一平面内,垂直于同一条直线的两条直线平行;
B.相等的角是对顶角;
C.两条直线被第三条直线所截,同位角相等;
D.和为180°的两个角叫做邻补角.
3.下列命题中的条件(题设)是什么?结论是什么?
(1)如果两个角相等,那么它们是对顶角;
(2)如果两条直线都与第三条直线平行,那么这两条直线也平行;
4.将下列命题改写成“如果……那么……”的形式,并判断正误.
(1)对顶角相等;
(2)同位角相等;
(3)同角的补角相等.
四、学习反思
本节课你有哪些收获?
第9课时5.4平移 导学案
班级: 姓名:
【学习目标】1了解平移的概念,知道生活中常见的平移例子;
2掌握平移的规律,会利用平移画图.
【学习重点】平移的规律,画图.?
【学习难点】利用平移的特征画图.
【学习过程】
一、学前准备
生活中有许多美丽的图案,他们都有着共同的特点,请同学们欣赏下面图案.
观察上面图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?请你试一试.
二、探索思考
探究一:请同学们仔细阅读课本P27~28页,你能发现并归纳平移的特征吗?
平移的特征:(1)把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小 ;
(2)新图形中的每一点,都是由原图形中的某一个点移动后得到的,这两个点是 ;
(3)连接各组对应点的线段平行(或在同一条直线上)且 .
即,在平面内,将一个图形沿 移动一定的 ,图形的这种移动,叫做平移变换,简称平移.
注意:图形平移的方向,不一定是水平的.图形经过平移后,_______图形的位置,________图形的形状,________图形的大小.(填“改变”或“不改变”)
练习一:
1.几何图形经过平移,图形中对应点所连的线段平行(或在同一条直线上)且 ,对应线段 且 ,对应角 .
2.平移改变的是图形的( ).
A.位置 B.形状 C.大小 D.位置、形状、大小
3.下列现象中,不属于平移的是( ).
A.滑雪运动员在的平坦雪地上滑行 B.大楼上上下下地迎送来客的电梯
C.钟摆的摆动 D.火车在笔直的铁轨上飞驰而过
4.下列各组图形,可经平移变换由一个图形得到另一个图形的是( ).
探究二:你能按要求将图形平移吗?动手试一试.
如图所示,把△ABC沿AB方向平移,平移的距离为线段a的长.
练习二:
1.如图所示,经过平移,四边形ABCD的顶点A移到点A′,作出平移后的四边形.
三、当堂反馈
1.一个图形先向右平移5个单位,再向左平移7个单位,所得到的图形可以看作是原来位置的图形一次性向_____平移______个单位得到.
2.∠DEF是∠ABC经过平移得到的,∠ABC=60°,则∠DEF=
3.如图,△ABC平移后得到了△A'B'C',其中点C的对应点是点C',已经标明,请你将点B'、点A'在图中标出来,并画出△A'B'C';若AB边上的中点为M,请你再标出点M的对应点M'.
4.已知△ABC、,过点D作△ABC平移后的图形,其中点D与点A对应.
四、学习反思
本节课你有哪些收获?
第10课时 相交线与平行线全章复习 导学案
班级: 姓名:
一、本章知识结构图
二、本章知识梳理
1.邻补角的定义: .
对顶角的定义: .
对顶角的性质: .
2.当两条直线相交所成的四个角中有一个为直角时,叫做这两条直线互相垂直,其中的一条直线叫 ,它们的交点叫 .
如图,用几何语言表示:
方式⑴∵ ∠AOC=90° ∴ AB_____CD,垂足是_____
方式⑵∵ AB⊥CD于O ∴ ∠AOC=______
3.在同一平面内,过一点有且只有_____条直线与已知直线垂直.
注意:垂线是 ,垂线段是一条 ,是图形.点到直线的
距离是 的长度,是一个数量,不能说“垂线段”是距离.
4.识别同位角、内错角、同旁内角的关键是要抓住“三线八角”,
只有“三线”出现且必须是两线被第三线所截才能出现这三类角;
位置1
位置2
结论
∠1和∠5
处于直线c的同侧
处于直线a、b的同一方
这样位置的一对角就称为( )
∠3和∠5
这样位置的一对角就称为( )
∠4和∠5
这样位置的一对角就称为( )
5. 现在所说的两条直线的位置关系,是两条直线在“ ”的前提下提出来的,它们的位置关系只有两种:一是 (有一个公共点),二是 (没有公共点).
6.平行线的定义:在同一平面内, 的两条直线叫做平行线.
平行公理:经过直线外一点, 一条直线与这条直线平行.
平行线的传递性:平行于同一直线的两直线 .
7.两条直线平行的判定方法:⑴平行线的定义,⑵平行线的传递性,
⑶平行线的判定公理:
⑷平行线的判定定理1:
⑸平行线的判定定理2:
⑹平行线的判定推论:
8.两条直线平行的性质:⑴根据平行线的定义
⑵平行线的性质公理:
⑶平行线的性质定理1:
⑷平行线的性质定理2:
⑸平行线间的距离 .
9.命题的定义:判断一件事情的语句,叫做命题.
每个命题都是由_______和______组成.每个命题都可以写成.“如果……,那么……”的形式,用“如果”开始的部份是 ,用“那么”开始的部份是 ,正确的命题叫做______,错误的命题叫做______.从长期的实践活动中总结出来的正确命题叫做 ,通过正确的推理得出的真命题叫做 .
10.平移的特征:(1)把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小 ;(2)新图形中的每一点,都是由原图形中的某一个点移动后得到的,这两个点是 ;(3)连接各组对应的线段 .即,在平面内,将一个图形沿 移动一定的 ,图形的这种移动,叫做平移变换,简称 .图形平移的方向,不一定是水平的.图形经过平移后,_______图形的位置,________图形的形状,________图形的大小.(填“改变”或“不改变”)
三、巩固练习
1.如图1,直线a,b相交于点O,若∠1=40°,则∠2等于_______.
图1 图2 图3 图4 图5
2.如图2,直线a∥b,∠1=123°30′,则∠2=______.
3.如图3,已知a∥b,∠1=70°,∠2=40°,则∠3=_____.
4.如图4,AB∥CD,∠E=40°,∠C=65°,则∠EAB的度数为( )
A.65° B.75° C.105° D.115°
5.如图5,直线L1与L2相交于点O,OM⊥L1,若α=44°,则β为( )
A.56° B.46° C.45° D.44°
6.如图6,AB∥CD,直线PQ分别交AB,CD于点E,F,FG是∠EFD的平分线,交AB于点G,若∠FEG=40°,那么∠FGB等于( )
A.80° B.100° C.110° D.120°
7.如图7,已知∠1=∠2=∠3=55°,则∠4的度数为( )
A.55° B.75° C.105° D.125°
第11课时 相交线与平行线 训练题
班级 姓名
【学习目标】理解相交线与平行线的意义, 掌握 命题的概念及结构,并会判断命题及真假
【学习重点】理解“三线八角” 掌握平行线的判定方法及性质。?
【学习难点】平行线的判定及性质的反复交错使用
A卷(基础知识部分,50分)
一、精心选一选(每题2分,共10分)
1.直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;(2)如果a∥b,b∥c,那么a∥c;(3)如果a∥b,b⊥c,那么a⊥c;(4)如果a与b相交,b与c相交,那么a 与c相交;在上述四种说法中,正确的有 ( )A.1个 B.2个 C.3个 D.4个
2.三条直线两两相交于同一点时,对顶角有m对,交于不同三点时,对顶角有n对,则m与n的关系是( ) A.m = n B.m>n C.m<n D.m + n = 10
3.A、B、C是直线l上的三点,P是直线l外一点.若PA=5cm、PB=6cm、PC=8cm.由此可知,点P到直线l的距离是 ( )A.5cm B.不小于5cm C.不大于5cm D.在6cm与8cm之间
4.平移后的图形与原图形对应点的连线段( )
A.相等 B.平行 C.平行且相等 D.平行且相等或在同一条直线上
5.如图,如果AC⊥BC,CD⊥AB,∠1=∠2,那么下列结论中正确的个数是( )
(1)∠1=∠B;(2)∠A=∠3;(3)AC∥DE;(4)∠2与∠B互余;(5)∠2=∠A;(6)A、C两点之间的距离就是线段AC的长; A.3个 B.4个 C.5个 D.6个
二、细心填一填(每题3分,共15分)
6.如图,AB∥CD,∠B=680,∠E=200,则∠D的度数为___________.
7.如图,由A测B的方向是_________________
8.如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是___________
9.如图,已知AB∥CD,∠1=30°,∠2=90°,则∠3等于_____________
10.把命题“等角的补角相等”改写成“如果……,那么……”的形式___________________.
三、耐心解一解(第11~13题各6分,第14题7分,共25分)
11.如图,EF∥AD,∠1 =∠2,∠BAC = 70°.将求∠AGD的过程填写完整.
因为EF∥AD,所以 ∠2 =______.又因为 ∠1 = ∠2,所以 ∠1 = ∠3. 所以AB∥____.所以∠BAC +______= 180°.又因为∠BAC = 70°,所以∠AGD =______.
12.已知三角形ABC、点D为点B平移后的对应点,过点D作三角形ABC平移后的图形
13.如图,已知直线AB、CD被直线EF所截,交AB,CD于点M、N,NH是一条射线,图中共有多少对同位角?多少对内错角?多少对同旁内角?分别指出这些角.
14.如图,∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?为什么?
B卷(激活训练部分,50分)
一、精心选一选(每题2分,共10分)
15.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是 ( )
A.第一次向右拐40°,第二次左拐140° B. 第一次向左拐40°,第二次右拐40°
C.第一次向左拐40°,第二次左拐140° D. 第一次向右拐40°,第二次右拐40°
16.将已知点P平移5cm后得到点P’,满足条件的点P’构成的图形是 ( )
A.一个点 B.两个点 C.一条5cm长的线段PP’ D.一个半径5cm的圆
17.如图,在5×5方格纸中将左图中的图形N平移后的位置右图中所示,那么正确的平移方法是( ).
A.先向下移动1格,再向左移动1格 B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格 D.先向下移动2格,再向左移动2格
18.如图,直线a∥b,点B在直线b上,且AB⊥BC ,∠1=55 o ,则∠2 的度数为( )
A . 35 o B . 45 o C . 55 o D . 125o
18 1917
19.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
二、细心填一填(每题3分,共15分)
20.把一副三角板按如图方式放置,则两条斜边所形成的钝角_______度.
20 21 22
21.如图,∠ABC和∠ACB的平分线BO与CO相交于点O,EF过点O,且EF∥BC,若∠BOC=130°,∠ABC∶∠ACB=3∶2,则∠AEF=_________,∠EFC=_________.
22.如图,直线AB∥CD,直线EF交AB于G,交CD于F,直线EH交AB于H.若∠1=45°,∠2=60°,则∠E的度数为________ 度.
23.如图,直线与直线互相平行,则的值是____________
23 24
24.如图,AB∥CD,∠A=120°,∠1=72°,则∠D的度数为__________.
三、耐心解一解(第25~27题各6分,第28题7分,共25分)
25.直线AB、CD相交于点O,OE⊥AB于O,且∠DOE=4∠COE,求∠AOD的度数.
26.如图,直线DE过点A,F是BA延长线上一点,具备什么条件时,可以判定DE∥BC?为什么?
27.已知:如图,AB∥CD,∠B=∠D. 求证:∠1=∠2
28.如图,已知∠1=∠2,再添上什么条件可使AB∥CD成立?并就你添上的条件证明AB∥CD .
第12课时 相交线与平行线 训练题
班级 姓名
【学习目标】理解相交线与平行线的意义, 掌握有关计算常用方法.
【学习重点】理解“三线八角” 掌握平行线的判定方法及性质。?
【学习难点】平行线的判定及性质的反复交错使用
一、填空题(每空2′,共2′×9)
1、如果∠A=35°18′,那么∠A的余角等于_____;
2、如图①,直线a、b被直线c所截(即直线c与直线a、b都相交),
且a∥b,若∠1=118°,则∠2的度数=_____;
3、一个角的补角比这个角的余角大___度;
4、推理填空,如图③∵∠B=___; ∴AB∥CD(____________);
∵∠DGF=___; ∴CD∥EF(____________);
∵AB∥EF; ∴∠B+___=180°(___________);
二、选择题(4′×2)
5、如果一个角的补角是150°,那么这个角的余角的度数是( )
A 30° B 60° C 90° D 120°
6、如图②,已知直线a、b被直线c所截,a∥b,∠1=50°,则∠2=( ) A 50° B 130° C 40° D 60°
下列各题期望你仔细阅读题目、明确已知与所需解决的问题,认真观察、思考、推断;其中有的知识是上学期学过的,你可能忘了,你重新复习这些知识好吗?
三、解答下列各题(60′)
7、(8′)如图④,在四边形ABCD中,已知AB∥CD,∠B=60°,你能求出哪些角的度数?
为什么?你能求出∠A的度数吗?
?
?
?
?
?8、(8′)如图⑤,在四边形ABCD中,已知∠B=60°,∠C=120°,由这些条件你能判断哪两条直线平行?说说你的理由。
?
?
?
?
9、(10′)如图⑥,已知∠1=30°,∠B=60°,AB⊥AC,
⑴∠DAB+∠B=_____;
⑵AB与CD平行吗?AD与BC平行吗?
10、(10′)如图⑦,∠1=∠2,能判断AB∥DF吗?为什么?若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由。
?
?
?11、(12′)如图⑧,BC∥DE,小颖用量角器分别画出∠ABC、∠ADE的角平分线BG、DH,想一想,小颖所画的这两条射线BG和DH会平行吗?为什么?(请你先用量角器画出这两条角平分线)
?
?
12、(12′)如图⑨,左图是一个三角形,已知∠ACB=90°,
那么∠A的余角是哪个角呢?答:___;
小明用三角尺在这个三角形中画了一条高CD(点D是垂足),得到右图?
?⑴请你帮小明画出这条高;
⑵在右图中,小明通过仔细观察、认真思考,找出了
三对余角,你能帮小明把它们写出来吗?
答:①_________;②_________;
③_________。
⑶∠ACB、∠ADC、∠CDB都是直角,所以∠ACB=∠ADC=∠CDB,小明还发现了另外两对相等的角,请你也仔细地观察、认真地思考分析,试一试,能发现吗?把它们写出来,并请说明理由。
?
?四、(6′)推理分析
13、一个小朋友的颜料盒中有6种不同颜色的彩笔,它们的颜色顺次是yellow,red,blue,tan,pink,green,并且名称都写在彩笔上。他用了其中1支彩笔给某个图形涂颜色,他用了哪支彩笔呢?这里有三个条件:第一,它的字母至少在3个以上,6个以下;第二,这个彩笔不在red旁边;第三,这支彩笔不是最后一个。 请你猜出是哪一支,并简说你的理由。
?
??五、(8′)找规律(先动手画画,然后思考分析从中找出规律)
14、平面内有若干条直线,当下列情形时,可将平面最多分成几部分:
⑴有一条直线时,最多分成 2 部分;
⑵有二条直线时,最多分成 2+2=4 部分;
⑶有三条直线时,最多分成________部分;
(n)有n条直线时,最多分成________部分。
?15.如图,在四边形ABCD中,∠A=104°-∠2,∠ABC=76°+∠2,BD⊥CD于D,EF⊥CD于F,能辨认∠1=∠2吗?试说明理由.
第13课时 相交线与平行线 训练题
班级 姓名
【学习目标】理解相交线与平行线的意义, 掌握有关计算常用方法.
【学习重点】理解“三线八角” 掌握平行线的判定方法及性质。?
【学习难点】平行线的判定及性质的反复交错使用
一、选择题(选择填空2分一题)
1、如果一个角的补角是150°,那么这个角的度数是( )
A. 30° B. 60° C.90° D.120°
2、如图,已知直线a、b被直线c所截,a∥b,∠1=130°,则 ∠2=( )
A. 130° B. 50° C.40° D.60°
3、下列说法错误的是( )
A.内错角相等,两直线平行. B.两直线平行,同旁内角互补.
C.相等的角是对顶角. D.等角的补角相等.
4、下列图中∠1和∠2是同位角的是( )
A. ⑴、⑵、⑶, B. ⑵、⑶、⑷, C. ⑶、⑷、⑸, D. ⑴、⑵、⑸
5、已知:如图, ∠1=∠2 , 则有( )
A.AB∥CD B.AE∥DF C. AB∥CD 且AE∥DF D.以上都不对
6、如图,直线AB与CD交于点O,OE⊥AB于O,图∠1与∠2的关系是( )
A.对顶角 B.互余 C.互补 D相等
7、如图,DH∥EG∥BC,且DC∥EF,那么图中和∠1相等的角的个数是( )
A.2, B. 4, C. 5, D. 6
8、如图,AB//CD,BC//DE,则∠B+∠D的值为( )
A.90° B.150° C.180° D. 以上都不对
9、如图,直线AB与CD相交于点O,OB平分∠DOE.若∠DOE=60 o,
则∠AOE的度数是( ) A.90° B.150° C.180° D. 不能确定
10、一束光线垂直照射在水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为( )
A.45o B.60o C.75o D.80o
11、(2009临沂)下列图形中,由,能得到的是( )
12、(2009年遂宁)如图,已知∠1=∠2,∠3=80O,则∠4=( )
A.80O B. 70O C. 60O D. 50O
13、(2009年娄底)如图1,已知AC∥ED,∠C=26°,∠CBE=37°,则∠BED的度数是 ( )?
A.63° B.83° C.73° D.53°?
14、(2009年桂林市、百色市)如图,在所标识的角中,同位角是( ).
A.和 B.和 C.和 D.和
15、(2009年肇庆市)如图,中,,DE 过点C,且,若,则∠B的度数( ) A.35° B.45 C.55° D.65°
16、(2009年崇左)如图,把矩形沿对折后使两部分重合,若,则=( ) A.110° B.115° C.120° D.130°
二、填空 1、用尺规作图时,用 画直线、射线和直线,用 画弧或圆。
2、黎老师家在小星家的北偏东 68 度,则小星家在黎老师家的南偏西 度 。
3、如图①,如果∠ = ∠ ,可得AD∥BC,你的根据是 。
4、如图②,∠1 = 82o,∠2 = 98o,∠3 = 80o,则∠4 = 度。
5、如图③,直线AB,CD,EF相交于点O,AB⊥CD,OG平分∠AOE,
∠FOD = 28o,则∠BOE = 度,∠AOG = 度。
6、一个角与它的补角之差是20o,则这个角的度数是 度。
7、如图④,AB∥CD,∠BAE = 120o,∠DCE = 30o,则∠AEC = 度。
8、如图⑤,OA⊥OB,OC⊥OD,O是垂足,∠BOC=55o,那么∠AOD= .
9、如图⑥中∠DAB和∠B是直线DE和BC被直线 所截而成的,称它们为 角。
10、把一张长方形纸条按图⑤中,那样折叠后,若得到∠AOB′= 70o,则∠B′OG = 。
三、解答题:(6分一题)
1、完成推理填空:如图:已知∠A=∠F,∠C=∠D,求证:BD∥CE 。
请你认真完成下面的填空。
证明:∵∠A=∠F ( 已知 )∴AC∥DF ( ___________ )
∴∠D=∠ ( _____________ )
又∵∠C=∠D ( 已知 ),∴∠1=∠C ( 等量代换 )
∴BD∥CE( )。
2、如图:已知AB∥A′B′,BC∥B′C′,那么∠B与∠B′有何关系?为什么?
3、如图:a∥b,∠1=122°,∠3=50°,求∠2和∠4的度数 。
4、如图 ,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E = 140o,
求∠BFD的度数?
5. 如图所示,已知∠E=∠DAB,∠F=∠C,请你简要说明
AB与CD是否平行。
6. 如图所示,已知∠DAC=∠ACB,∠D=62°,求∠BCD的度数。
7、(2009年淄博市)如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37o,求∠D的度数.
