4.4幂函数 课件(共40张PPT)
文档属性
| 名称 | 4.4幂函数 课件(共40张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 06:19:37 | ||
图片预览











文档简介
(共40张PPT)
幂函数
必备知识·自主学习
1.幂函数的概念
一般地,我们把形如_____的函数称为幂函数,其中__是自变量,___是常数.
导思 1.除了一次函数、二次函数、反比例函数外还有哪些常见函数
2.幂函数有哪些特征
y=xα
x
α
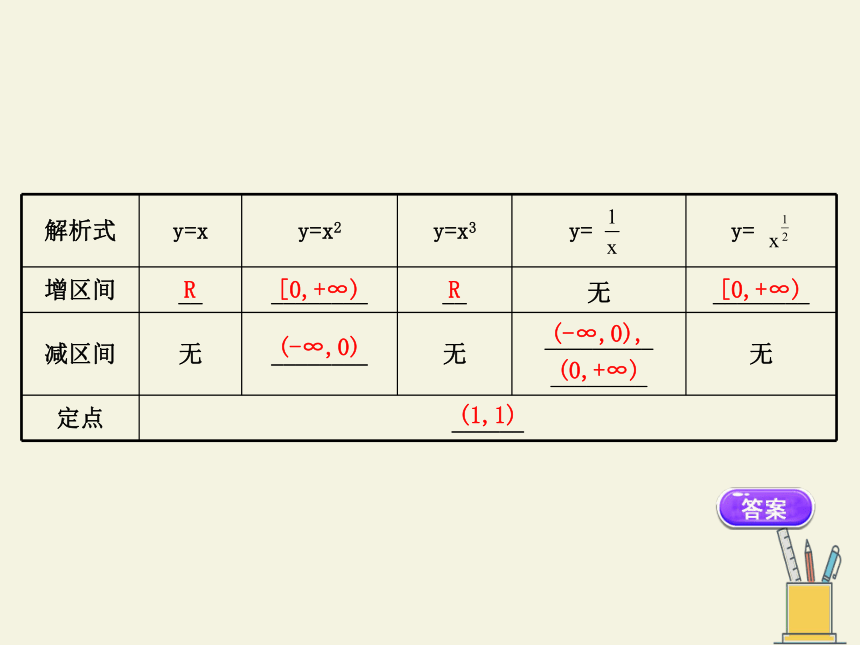
2.常见幂函数的图象与性质
解析式 y=x y=x2 y=x3 y= y=
图象
定义域 R R R _________ ________
值域 R ________ R _________ ________
奇偶性 ___函数 ___函数 ___函数 ___函数 _________
函数
{x|x≠0}
[0,+∞)
[0,+∞)
{y|y≠0}
[0,+∞)
奇
偶
奇
奇
非奇非偶
解析式 y=x y=x2 y=x3 y= y=
增区间 __ ________ __ 无 ________
减区间 无 ________ 无 _________ ________ 无
定点 ______
R
[0,+∞)
R
[0,+∞)
(-∞,0)
(-∞,0),
(0,+∞)
(1,1)
(1)本质:幂函数的图象是函数的图形表示,幂函数的性质是根据函数图象总结得到的.
(2)应用:①求定义域;②求值域;③比较大小;④求单调区间.
【思考】
在区间(0,+∞)上,幂函数有怎样的单调性
提示:幂函数在区间(0,+∞)上,当α>0时,y=xα是增函数;当α<0时,y=xα是减函数.
【基础小测】
1.辨析记忆(对的打“√”,错的打“×”)
(1)幂函数的图象必过点(0,0)和(1,1). ( )
(2)幂函数的图象都不过第二、四象限. ( )
(3)y= 与y= 定义域相同. ( )
提示:(1)×,幂函数y= 不过点(0,0).
(2)×,幂函数y=x2过第二象限.
(3)×,y= 的定义域为[0,+∞),而y= 的定义域为R.
2.下列函数中不是幂函数的是( )
A.y= B.y=x3
C.y=3x D.y=x-1
【解析】选C.只有y=3x不符合幂函数y=xα的形式.
3.已知幂函数 在 上为增函数,则实数m的值为
( )
A. B.±2 C.2 D.-2
【解析】选D.由于 为幂函数,所以m2-3=1,m=±2,当m=2时, =x-2在
上为减函数,不符合题意,当m=-2时 =x2在 上为增函数,符
合题意.
关键能力·合作学习
类型一 幂函数的概念(数学抽象)
【题组训练】
1.在函数y= y=3x2,y=x2+2x,y=1中,幂函数的个数为( )
A.0 B.1 C.2 D.3
2.(2020·吉林高一检测)函数f(x)=(2m-3) 是幂函数,则m的值为( )
A.2 B.-1 C.0 D.1
3.已知幂函数f(x)=xα的图象过点 则f(4)=________.
【解析】1.选B.函数y= =x-4为幂函数;
函数y=3x2中x2的系数不是1,所以它不是幂函数;
函数y=x2+2x不是y=xα(α是常数)的形式,
所以它不是幂函数;函数y=1与y=x0=1(x≠0)不相等,所以y=1不是幂函数.
2.选A.由于函数f(x)=(2m-3) 是幂函数,
故2m-3=1,所以m=2.
3.由f(2)= 可知2α= ,即α=- ,
所以f(4)=
答案:
【解题策略】
判断一个函数是否为幂函数的方法
判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,即函数的解析式为一个幂的形式,且需满足:(1)指数为常数;(2)底数为自变量;
(3)系数为1.
【补偿训练】
下列函数中是幂函数的是( )
①y= ②y=axm(a,m为非零常数,且a≠1);
③y= +x4;④y=xn;⑤y=(x-6)3;⑥y=8x2;⑦y=x2+x.
A.①②③ B.①④
C.③④⑤⑥ D.②④⑦
【解析】选B.由幂函数的定义:形如y=xα(α∈R)的函数才是幂函数,则y=
=x-3,y=xn是幂函数.
类型二 幂函数图象的应用(数学抽象、直观想象)
【题组训练】
1.函数y= 的图象是( )
【解析】选B.因为函数y= 是幂函数,幂函数在第一象限内恒过点(1,1),排
除A,D.当x>1,0<α<1时,y=xα在直线y=x下方,排除C.
2.若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则a,b,c,d的
大小关系是( )
A.d>c>b>a B.d>c>a>b
C.a>b>c>d D.a>b>d>c
【解析】选C.在第一象限内,x=1的右侧部分的图象,图象由下至上,幂指数增大,所以a>b>c>d.
3.已知幂函数f(x)=(m2-2m+1) 的图象不过原点,则m的值为( )
A.0 B.-1 C.2 D.0或2
【解析】选A.由幂函数定义可知m2-2m+1=1,
所以m=0或m=2;
当m=0时,f(x)=x-2,定义域为(-∞,0)∪(0,+∞);
当m=2时,f(x)=x4定义域为R;
又因为f(x)=(m2-2m+1) 的图象不过原点;
所以m2+m-2<0,所以m=0.
【解题策略】
解决幂函数图象问题应把握的两个原则
(1)依据图象高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图
象越靠近x轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图象越远离x轴
(简记为指大图高).
(2)依据图象确定幂指数α与0,1的大小关系,即根据幂函数在第一象限内的图
象(类似于y=x-1或y= 或y=x3)来判断.
【补偿训练】
在同一坐标系内,函数y=xa(a≠0)和y=ax- 的图象可能是( )
【解析】选C.选项A中,幂函数的指数a<0,则直线y=ax- 应为减函数,A错误;
选项B中,幂函数的指数a>1,则直线y=ax- 应为增函数,B错误;
选项D中,幂函数的指数a<0,则- >0,直线y=ax- 在y轴上的截距为正,D错误.
类型三 幂函数性质的综合应用(数学抽象、逻辑推理)
角度1 比较大小
【典例】比较下列各组中幂值的大小:
(1)0.213,0.233;(2)
【思路导引】构造幂函数,借助其单调性求解.
【解析】(1)因为函数y=x3是增函数,且0.21<0.23,
所以0.213<0.233.
(2)
因为1.2> >1.1,且y= 在[0,+∞)上单调递增,
所以 即
【变式探究】
把本例的各组数据更换如下,再比较其大小关系:
【解析】(1)因为幂函数y=x0.5在[0,+∞)上是单调递增的,又 所以
(2)因为幂函数y=x-1在(-∞,0)上是单调递减的,又 所以
角度2 幂函数性质的综合应用
【典例】已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称且在(0,+∞)上单调递减,
求满足 < 的a的取值范围.
【思路导引】根据函数的图象关于y轴对称且在(0,+∞)上单调递减及m∈N*求出
m的值,代入不等式解不等式即可,解不等式时注意幂函数的定义域.
【解析】因为函数在(0,+∞)上单调递减,
所以3m-9<0,解得m<3.
又因为m∈N*,所以m=1,2.
因为函数的图象关于y轴对称,
所以3m-9为偶数,故m=1.
则原不等式可化为
因为y= 在(-∞,0),(0,+∞)上单调递减,
所以a+1>3-2a>0或3-2a故a的取值范围是
【解题策略】
幂函数常用性质
(1)幂函数y=xα 奇偶性的判断方法:
①若p,q同为奇数,则y=xα为奇函数.
②若p为奇数,q为偶数,则y=xα为偶函数.
③若p为偶数,则y=xα为非奇非偶函数.
(2)幂函数单调性判断:
幂函数y=xα在区间(0,+∞)上,当α>0时,y=xα是增函数;当α<0时,y=xα是减
函数.
【题组训练】
1.比较大小: ________
【解析】因为y= 为(0,+∞)上的减函数,且
所以 >
答案:>
2.函数f(x)=x2(x<0)的奇偶性为 ( )
A.奇函数
B.偶函数
C.既是奇函数又是偶函数
D.非奇非偶函数
【解析】选D.因为函数f(x)=x2(x<0)的定义域为(-∞,0),不关于原点对称,
所以函数f(x)=x2(x<0)为非奇非偶函数.
3.已知幂函数f(x)=(m2-3m+3)xm+1为偶函数,则m=( )
A.1 B.2 C.1或2 D.3
【解析】选A.因为幂函数f(x)=(m2-3m+3)xm+1为偶函数,所以m2-3m+3=1,即m2-3m+2=0,解得m=1或m=2.当m=1时,幂函数f(x)=x2为偶函数,满足条件.当m=2时,幂函数f(x)=x3为奇函数,不满足条件.
【补偿训练】
已知幂函数f(x)= (m∈Z)的图象与x轴,y轴都无交点,且关于原点对称,则
函数f(x)的解析式是________.
【解析】因为函数的图象与x轴,y轴都无交点,
所以m2-1<0,解得-1因为图象关于原点对称,且m∈Z,所以m=0,
所以f(x)=x-1.
答案:f(x)=x-1
课堂检测·素养达标
1.下列函数是幂函数的是( )
A.y= B.y=x5
C.y=5x D.y=(x+1)3
【解析】选B.函数y= 和y=5x是正比例函数,不是幂函数;函数y=(x+1)3的底
数不是自变量x,不是幂函数;函数y=x5是幂函数.
2.如图所示,给出4个幂函数的图象,则图象与函数的大致对应是 ( )
A.①y= ②y=x2,③y= ④y=x-1
B.①y=x3,②y=x2,③y= ④y=x-1
C.①y=x2,②y=x3,③y= ④y=x-1
D.①y=x3,②y= ③y=x2,④y=x-1
【解析】选B.因为y=x3的定义域为R且为奇函数,故应为图①;y=x2为开口向上的抛物线且顶点为原点,应为图②.同理可得出选项B正确.
3.(教材二次开发:习题改编)幂函数f(x)的图象过点(3, ),则f(8)=
( )
A.8 B.6 C.4 D.2
【解析】选C.设幂函数f(x)=xα(α为常数),由函数的图象过点(3, ),可得
=3α,所以α= 则幂函数f(x)= 所以f(8)= =4.
4.判断大小: ________ (填“>”或“<”)
【解析】因为y= 为[0,+∞)上的增函数,
且2.3<2.4,所以 <
答案:<
5.(2020·南京高一检测)已知幂函数f(x)= (m∈N*)的图象经过点(2,8).
(1)试确定m的值;
(2)求满足条件f(2-a)>f(a-1)的实数a的取值范围.
【解析】(1)由题得 =8 m=1或m=-2(舍).
(2)由题得f(x)=x3,f(x)在R上为增函数,
由f(2-a)>f(a-1)可得2-a>a-1 a< .
谢 谢
幂函数
必备知识·自主学习
1.幂函数的概念
一般地,我们把形如_____的函数称为幂函数,其中__是自变量,___是常数.
导思 1.除了一次函数、二次函数、反比例函数外还有哪些常见函数
2.幂函数有哪些特征
y=xα
x
α
2.常见幂函数的图象与性质
解析式 y=x y=x2 y=x3 y= y=
图象
定义域 R R R _________ ________
值域 R ________ R _________ ________
奇偶性 ___函数 ___函数 ___函数 ___函数 _________
函数
{x|x≠0}
[0,+∞)
[0,+∞)
{y|y≠0}
[0,+∞)
奇
偶
奇
奇
非奇非偶
解析式 y=x y=x2 y=x3 y= y=
增区间 __ ________ __ 无 ________
减区间 无 ________ 无 _________ ________ 无
定点 ______
R
[0,+∞)
R
[0,+∞)
(-∞,0)
(-∞,0),
(0,+∞)
(1,1)
(1)本质:幂函数的图象是函数的图形表示,幂函数的性质是根据函数图象总结得到的.
(2)应用:①求定义域;②求值域;③比较大小;④求单调区间.
【思考】
在区间(0,+∞)上,幂函数有怎样的单调性
提示:幂函数在区间(0,+∞)上,当α>0时,y=xα是增函数;当α<0时,y=xα是减函数.
【基础小测】
1.辨析记忆(对的打“√”,错的打“×”)
(1)幂函数的图象必过点(0,0)和(1,1). ( )
(2)幂函数的图象都不过第二、四象限. ( )
(3)y= 与y= 定义域相同. ( )
提示:(1)×,幂函数y= 不过点(0,0).
(2)×,幂函数y=x2过第二象限.
(3)×,y= 的定义域为[0,+∞),而y= 的定义域为R.
2.下列函数中不是幂函数的是( )
A.y= B.y=x3
C.y=3x D.y=x-1
【解析】选C.只有y=3x不符合幂函数y=xα的形式.
3.已知幂函数 在 上为增函数,则实数m的值为
( )
A. B.±2 C.2 D.-2
【解析】选D.由于 为幂函数,所以m2-3=1,m=±2,当m=2时, =x-2在
上为减函数,不符合题意,当m=-2时 =x2在 上为增函数,符
合题意.
关键能力·合作学习
类型一 幂函数的概念(数学抽象)
【题组训练】
1.在函数y= y=3x2,y=x2+2x,y=1中,幂函数的个数为( )
A.0 B.1 C.2 D.3
2.(2020·吉林高一检测)函数f(x)=(2m-3) 是幂函数,则m的值为( )
A.2 B.-1 C.0 D.1
3.已知幂函数f(x)=xα的图象过点 则f(4)=________.
【解析】1.选B.函数y= =x-4为幂函数;
函数y=3x2中x2的系数不是1,所以它不是幂函数;
函数y=x2+2x不是y=xα(α是常数)的形式,
所以它不是幂函数;函数y=1与y=x0=1(x≠0)不相等,所以y=1不是幂函数.
2.选A.由于函数f(x)=(2m-3) 是幂函数,
故2m-3=1,所以m=2.
3.由f(2)= 可知2α= ,即α=- ,
所以f(4)=
答案:
【解题策略】
判断一个函数是否为幂函数的方法
判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,即函数的解析式为一个幂的形式,且需满足:(1)指数为常数;(2)底数为自变量;
(3)系数为1.
【补偿训练】
下列函数中是幂函数的是( )
①y= ②y=axm(a,m为非零常数,且a≠1);
③y= +x4;④y=xn;⑤y=(x-6)3;⑥y=8x2;⑦y=x2+x.
A.①②③ B.①④
C.③④⑤⑥ D.②④⑦
【解析】选B.由幂函数的定义:形如y=xα(α∈R)的函数才是幂函数,则y=
=x-3,y=xn是幂函数.
类型二 幂函数图象的应用(数学抽象、直观想象)
【题组训练】
1.函数y= 的图象是( )
【解析】选B.因为函数y= 是幂函数,幂函数在第一象限内恒过点(1,1),排
除A,D.当x>1,0<α<1时,y=xα在直线y=x下方,排除C.
2.若四个幂函数y=xa,y=xb,y=xc,y=xd在同一坐标系中的图象如图,则a,b,c,d的
大小关系是( )
A.d>c>b>a B.d>c>a>b
C.a>b>c>d D.a>b>d>c
【解析】选C.在第一象限内,x=1的右侧部分的图象,图象由下至上,幂指数增大,所以a>b>c>d.
3.已知幂函数f(x)=(m2-2m+1) 的图象不过原点,则m的值为( )
A.0 B.-1 C.2 D.0或2
【解析】选A.由幂函数定义可知m2-2m+1=1,
所以m=0或m=2;
当m=0时,f(x)=x-2,定义域为(-∞,0)∪(0,+∞);
当m=2时,f(x)=x4定义域为R;
又因为f(x)=(m2-2m+1) 的图象不过原点;
所以m2+m-2<0,所以m=0.
【解题策略】
解决幂函数图象问题应把握的两个原则
(1)依据图象高低判断幂指数大小,相关结论为:在(0,1)上,指数越大,幂函数图
象越靠近x轴(简记为指大图低);在(1,+∞)上,指数越大,幂函数图象越远离x轴
(简记为指大图高).
(2)依据图象确定幂指数α与0,1的大小关系,即根据幂函数在第一象限内的图
象(类似于y=x-1或y= 或y=x3)来判断.
【补偿训练】
在同一坐标系内,函数y=xa(a≠0)和y=ax- 的图象可能是( )
【解析】选C.选项A中,幂函数的指数a<0,则直线y=ax- 应为减函数,A错误;
选项B中,幂函数的指数a>1,则直线y=ax- 应为增函数,B错误;
选项D中,幂函数的指数a<0,则- >0,直线y=ax- 在y轴上的截距为正,D错误.
类型三 幂函数性质的综合应用(数学抽象、逻辑推理)
角度1 比较大小
【典例】比较下列各组中幂值的大小:
(1)0.213,0.233;(2)
【思路导引】构造幂函数,借助其单调性求解.
【解析】(1)因为函数y=x3是增函数,且0.21<0.23,
所以0.213<0.233.
(2)
因为1.2> >1.1,且y= 在[0,+∞)上单调递增,
所以 即
【变式探究】
把本例的各组数据更换如下,再比较其大小关系:
【解析】(1)因为幂函数y=x0.5在[0,+∞)上是单调递增的,又 所以
(2)因为幂函数y=x-1在(-∞,0)上是单调递减的,又 所以
角度2 幂函数性质的综合应用
【典例】已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称且在(0,+∞)上单调递减,
求满足 < 的a的取值范围.
【思路导引】根据函数的图象关于y轴对称且在(0,+∞)上单调递减及m∈N*求出
m的值,代入不等式解不等式即可,解不等式时注意幂函数的定义域.
【解析】因为函数在(0,+∞)上单调递减,
所以3m-9<0,解得m<3.
又因为m∈N*,所以m=1,2.
因为函数的图象关于y轴对称,
所以3m-9为偶数,故m=1.
则原不等式可化为
因为y= 在(-∞,0),(0,+∞)上单调递减,
所以a+1>3-2a>0或3-2a
【解题策略】
幂函数常用性质
(1)幂函数y=xα 奇偶性的判断方法:
①若p,q同为奇数,则y=xα为奇函数.
②若p为奇数,q为偶数,则y=xα为偶函数.
③若p为偶数,则y=xα为非奇非偶函数.
(2)幂函数单调性判断:
幂函数y=xα在区间(0,+∞)上,当α>0时,y=xα是增函数;当α<0时,y=xα是减
函数.
【题组训练】
1.比较大小: ________
【解析】因为y= 为(0,+∞)上的减函数,且
所以 >
答案:>
2.函数f(x)=x2(x<0)的奇偶性为 ( )
A.奇函数
B.偶函数
C.既是奇函数又是偶函数
D.非奇非偶函数
【解析】选D.因为函数f(x)=x2(x<0)的定义域为(-∞,0),不关于原点对称,
所以函数f(x)=x2(x<0)为非奇非偶函数.
3.已知幂函数f(x)=(m2-3m+3)xm+1为偶函数,则m=( )
A.1 B.2 C.1或2 D.3
【解析】选A.因为幂函数f(x)=(m2-3m+3)xm+1为偶函数,所以m2-3m+3=1,即m2-3m+2=0,解得m=1或m=2.当m=1时,幂函数f(x)=x2为偶函数,满足条件.当m=2时,幂函数f(x)=x3为奇函数,不满足条件.
【补偿训练】
已知幂函数f(x)= (m∈Z)的图象与x轴,y轴都无交点,且关于原点对称,则
函数f(x)的解析式是________.
【解析】因为函数的图象与x轴,y轴都无交点,
所以m2-1<0,解得-1
所以f(x)=x-1.
答案:f(x)=x-1
课堂检测·素养达标
1.下列函数是幂函数的是( )
A.y= B.y=x5
C.y=5x D.y=(x+1)3
【解析】选B.函数y= 和y=5x是正比例函数,不是幂函数;函数y=(x+1)3的底
数不是自变量x,不是幂函数;函数y=x5是幂函数.
2.如图所示,给出4个幂函数的图象,则图象与函数的大致对应是 ( )
A.①y= ②y=x2,③y= ④y=x-1
B.①y=x3,②y=x2,③y= ④y=x-1
C.①y=x2,②y=x3,③y= ④y=x-1
D.①y=x3,②y= ③y=x2,④y=x-1
【解析】选B.因为y=x3的定义域为R且为奇函数,故应为图①;y=x2为开口向上的抛物线且顶点为原点,应为图②.同理可得出选项B正确.
3.(教材二次开发:习题改编)幂函数f(x)的图象过点(3, ),则f(8)=
( )
A.8 B.6 C.4 D.2
【解析】选C.设幂函数f(x)=xα(α为常数),由函数的图象过点(3, ),可得
=3α,所以α= 则幂函数f(x)= 所以f(8)= =4.
4.判断大小: ________ (填“>”或“<”)
【解析】因为y= 为[0,+∞)上的增函数,
且2.3<2.4,所以 <
答案:<
5.(2020·南京高一检测)已知幂函数f(x)= (m∈N*)的图象经过点(2,8).
(1)试确定m的值;
(2)求满足条件f(2-a)>f(a-1)的实数a的取值范围.
【解析】(1)由题得 =8 m=1或m=-2(舍).
(2)由题得f(x)=x3,f(x)在R上为增函数,
由f(2-a)>f(a-1)可得2-a>a-1 a< .
谢 谢
