4.4幂函数 课件(共25张PPT)
文档属性
| 名称 | 4.4幂函数 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 896.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 08:55:30 | ||
图片预览







文档简介
(共25张PPT)
幂函数
1.理解幂函数的概念;
2.学会以简单的幂函数为例研究函数性质的方法;
3.理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数有关问题.
问题导学
题型探究
达标检测
学习目标
问题导学 新知探究 点点落实
知识点一 幂函数的概念
答案 底数为x,指数为常数.
答案
一般地, 叫做幂函数,其中x是自变量,α是常数.
函数y=xα
知识点二 幂函数的图象与性质
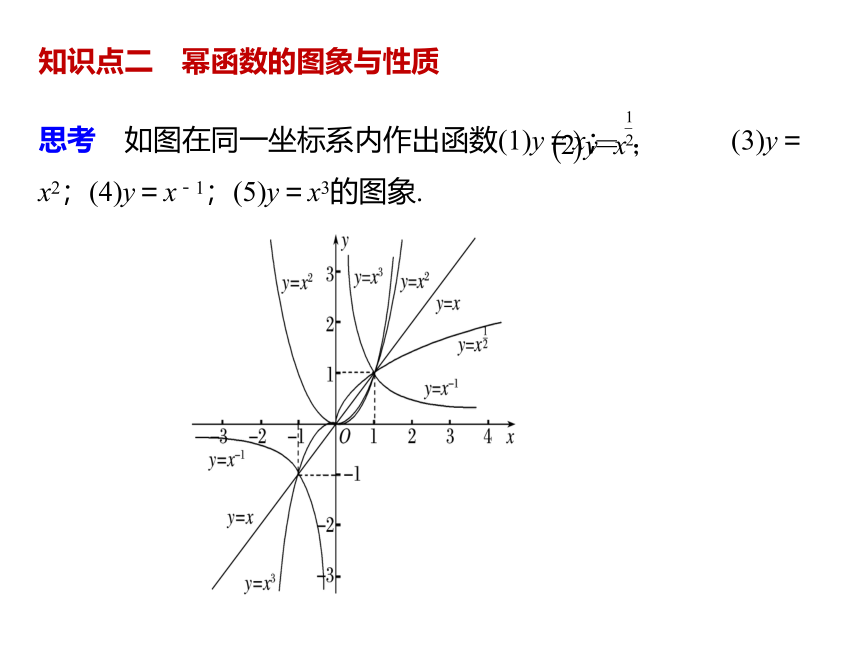
思考 如图在同一坐标系内作出函数(1)y=x; (3)y=x2;(4)y=x-1;(5)y=x3的图象.
答案
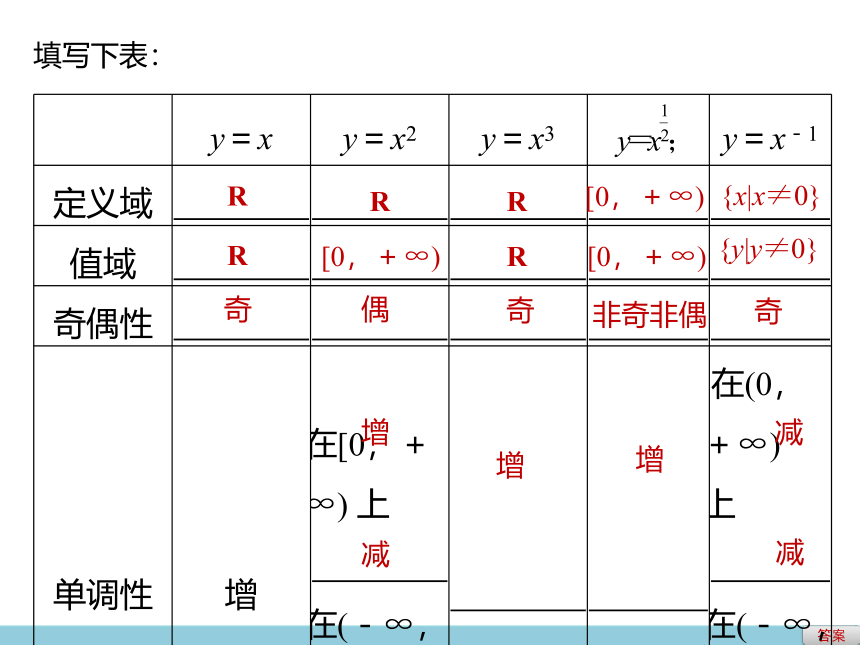
填写下表:
y=x y=x2 y=x3 y=x-1
定义域
值域
奇偶性
单调性 增 在[0,+∞) 上 ,在(-∞,0] 上 在(0,+∞) 上 ,在(-∞,0) 上____
R
R
R
[0,+∞)
{x|x≠0}
[0,+∞)
R
R
[0,+∞)
{y|y≠0}
奇
偶
奇
非奇非偶
奇
增
减
增
增
减
减
根据上表,可以归纳一般幂函数特征:
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都过点 ;
(2)α>0时,幂函数的图象通过 ,并且在区间[0,+∞)上是 函数.特别地,当α>1时,幂函数的图象 ;当0<α<1时,幂函数的图象 ;
(3) 时,幂函数的图象在区间(0,+∞)上是减函数;
(4)幂指数互为倒数的幂函数在第一象限内的图象关于直线y=x对称;
(5)在第一象限,作直线x=a(a>1),它同各幂函数图象相交,按交点从下到上的顺序,幂指数按从 到 的顺序排列.
答案
(1,1)
原点
增
下凸
上凸
α<0
小
大
返回
题型探究 重点难点 个个击破
类型一 幂函数的概念
例1 已知 是幂函数,求m,n的值.
解析答案
反思与感悟
反思与感悟
解析答案
A.0 B.1 C.2 D.3
y=2x2由于出现系数2,因此不是幂函数;
y=x2+x是两项和的形式,不是幂函数;y=1=x0(x≠0),可以看出,常函数y=1的图象比幂函数y=x0的图象多了一个点(0,1),
所以常函数y=1不是幂函数.
B
类型二 幂函数的图象及应用
解析答案
反思与感悟
则f(x)=x2.同理可求得g(x)=x-2.
在同一坐标系里作出函数f(x)=x2和g(x)=x-2的图象(如图所示),
观察图象可得:
(1)当x>1或x<-1时,f(x)>g(x);
(2)当x=1或x=-1时,f(x)=g(x);
(3)当-1反思与感悟
反思与感悟
注意本题中对f(x)>g(x),f(x)=g(x)的几何解释.这种几何解释帮助我们从图形角度解读不等式方程,是以后常用的方法.
解析答案
跟踪训练2 幂函数y=xα(α≠0),当α取不同的正数时,在区间[0,1]上它们的图象是一簇美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图象三等分,即有BM=MN=NA.那么αβ等于( )
A.1 B.2 C.3 D.无法确定
∴αβ=1.故选A.
A
类型三 幂函数性质的综合应用
例3 (1)探讨函数 的单调性.
解析答案
解 的定义域为(0,+∞).
任取x1,x2∈(0,+∞),且x1因为x2>x1>0,所以x1-x2<0,
所以 在区间(0,+∞)内是减函数.
解析答案
(2)若 则a的取值范围是________.
解析 由(1)知 在区间(0,+∞)内是减函数.
反思与感悟
反思与感悟
本例第(2)问是核心问题,第(1)问是铺垫,很多时候,我们会直接面对没有第(1)问的第(2)问,这个时候需要我们主动构造函数,并针对解题需要研究某方面的性质.
解析答案
跟踪训练3 已知幂函数
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
解 ∵m∈N*,
∴m2+m=m×(m+1)为偶数.
∴定义域为[0,+∞),在[0,+∞)上f(x)为增函数.
解析答案
返回
解
∴m2+m=2,
解得m=1或m=-2(舍去),
由(1)知f(x)在定义域[0,+∞)上为增函数.
∴f(2-a)>f(a-1)等价于2-a>a-1≥0,
1
2
3
达标检测
4
5
解析答案
C
1
2
3
4
5
答案
D
1
2
3
4
5
A.1,3 B.-1,1
C.-1,3 D.-1,1,3
答案
A
1
2
3
4
5
4.下列是 的图象的是( )
答案
B
1
2
3
4
5
5.以下结论正确的是( )
A.当α=0时,函数y=xα的图象是一条直线
B.幂函数的图象都经过(0,0),(1,1)两点
C.若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大
而增大
D.幂函数的图象不可能在第四象限,但可能在第二象限
答案
D
规律与方法
1.幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的底x为自变量,指数α为常数,这是判断一个函数是不是幂函数的重要依据和唯一标准.
2.幂函数y=xα的图象与性质由于α的值不同而比较复杂,一般从两个方面考查:(1)α>0时,图象过(0,0),(1,1)在第一象限的图象上升;α<0时,图象不过原点,在第一象限的图象下降,反之也成立.(2)曲线在第一象限的凹凸性α>1时,曲线下凸;0<α<1时,曲线上凸;α<0时,曲线下凸.
返回
幂函数
1.理解幂函数的概念;
2.学会以简单的幂函数为例研究函数性质的方法;
3.理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数有关问题.
问题导学
题型探究
达标检测
学习目标
问题导学 新知探究 点点落实
知识点一 幂函数的概念
答案 底数为x,指数为常数.
答案
一般地, 叫做幂函数,其中x是自变量,α是常数.
函数y=xα
知识点二 幂函数的图象与性质
思考 如图在同一坐标系内作出函数(1)y=x; (3)y=x2;(4)y=x-1;(5)y=x3的图象.
答案
填写下表:
y=x y=x2 y=x3 y=x-1
定义域
值域
奇偶性
单调性 增 在[0,+∞) 上 ,在(-∞,0] 上 在(0,+∞) 上 ,在(-∞,0) 上____
R
R
R
[0,+∞)
{x|x≠0}
[0,+∞)
R
R
[0,+∞)
{y|y≠0}
奇
偶
奇
非奇非偶
奇
增
减
增
增
减
减
根据上表,可以归纳一般幂函数特征:
(1)所有的幂函数在(0,+∞)上都有定义,并且图象都过点 ;
(2)α>0时,幂函数的图象通过 ,并且在区间[0,+∞)上是 函数.特别地,当α>1时,幂函数的图象 ;当0<α<1时,幂函数的图象 ;
(3) 时,幂函数的图象在区间(0,+∞)上是减函数;
(4)幂指数互为倒数的幂函数在第一象限内的图象关于直线y=x对称;
(5)在第一象限,作直线x=a(a>1),它同各幂函数图象相交,按交点从下到上的顺序,幂指数按从 到 的顺序排列.
答案
(1,1)
原点
增
下凸
上凸
α<0
小
大
返回
题型探究 重点难点 个个击破
类型一 幂函数的概念
例1 已知 是幂函数,求m,n的值.
解析答案
反思与感悟
反思与感悟
解析答案
A.0 B.1 C.2 D.3
y=2x2由于出现系数2,因此不是幂函数;
y=x2+x是两项和的形式,不是幂函数;y=1=x0(x≠0),可以看出,常函数y=1的图象比幂函数y=x0的图象多了一个点(0,1),
所以常函数y=1不是幂函数.
B
类型二 幂函数的图象及应用
解析答案
反思与感悟
则f(x)=x2.同理可求得g(x)=x-2.
在同一坐标系里作出函数f(x)=x2和g(x)=x-2的图象(如图所示),
观察图象可得:
(1)当x>1或x<-1时,f(x)>g(x);
(2)当x=1或x=-1时,f(x)=g(x);
(3)当-1
反思与感悟
注意本题中对f(x)>g(x),f(x)=g(x)的几何解释.这种几何解释帮助我们从图形角度解读不等式方程,是以后常用的方法.
解析答案
跟踪训练2 幂函数y=xα(α≠0),当α取不同的正数时,在区间[0,1]上它们的图象是一簇美丽的曲线(如图).设点A(1,0),B(0,1),连接AB,线段AB恰好被其中的两个幂函数y=xα,y=xβ的图象三等分,即有BM=MN=NA.那么αβ等于( )
A.1 B.2 C.3 D.无法确定
∴αβ=1.故选A.
A
类型三 幂函数性质的综合应用
例3 (1)探讨函数 的单调性.
解析答案
解 的定义域为(0,+∞).
任取x1,x2∈(0,+∞),且x1
所以 在区间(0,+∞)内是减函数.
解析答案
(2)若 则a的取值范围是________.
解析 由(1)知 在区间(0,+∞)内是减函数.
反思与感悟
反思与感悟
本例第(2)问是核心问题,第(1)问是铺垫,很多时候,我们会直接面对没有第(1)问的第(2)问,这个时候需要我们主动构造函数,并针对解题需要研究某方面的性质.
解析答案
跟踪训练3 已知幂函数
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
解 ∵m∈N*,
∴m2+m=m×(m+1)为偶数.
∴定义域为[0,+∞),在[0,+∞)上f(x)为增函数.
解析答案
返回
解
∴m2+m=2,
解得m=1或m=-2(舍去),
由(1)知f(x)在定义域[0,+∞)上为增函数.
∴f(2-a)>f(a-1)等价于2-a>a-1≥0,
1
2
3
达标检测
4
5
解析答案
C
1
2
3
4
5
答案
D
1
2
3
4
5
A.1,3 B.-1,1
C.-1,3 D.-1,1,3
答案
A
1
2
3
4
5
4.下列是 的图象的是( )
答案
B
1
2
3
4
5
5.以下结论正确的是( )
A.当α=0时,函数y=xα的图象是一条直线
B.幂函数的图象都经过(0,0),(1,1)两点
C.若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大
而增大
D.幂函数的图象不可能在第四象限,但可能在第二象限
答案
D
规律与方法
1.幂函数y=xα(α∈R),其中α为常数,其本质特征是以幂的底x为自变量,指数α为常数,这是判断一个函数是不是幂函数的重要依据和唯一标准.
2.幂函数y=xα的图象与性质由于α的值不同而比较复杂,一般从两个方面考查:(1)α>0时,图象过(0,0),(1,1)在第一象限的图象上升;α<0时,图象不过原点,在第一象限的图象下降,反之也成立.(2)曲线在第一象限的凹凸性α>1时,曲线下凸;0<α<1时,曲线上凸;α<0时,曲线下凸.
返回
