4.4幂函数 学案(Word版无答案)
文档属性
| 名称 | 4.4幂函数 学案(Word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 78.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 09:04:29 | ||
图片预览

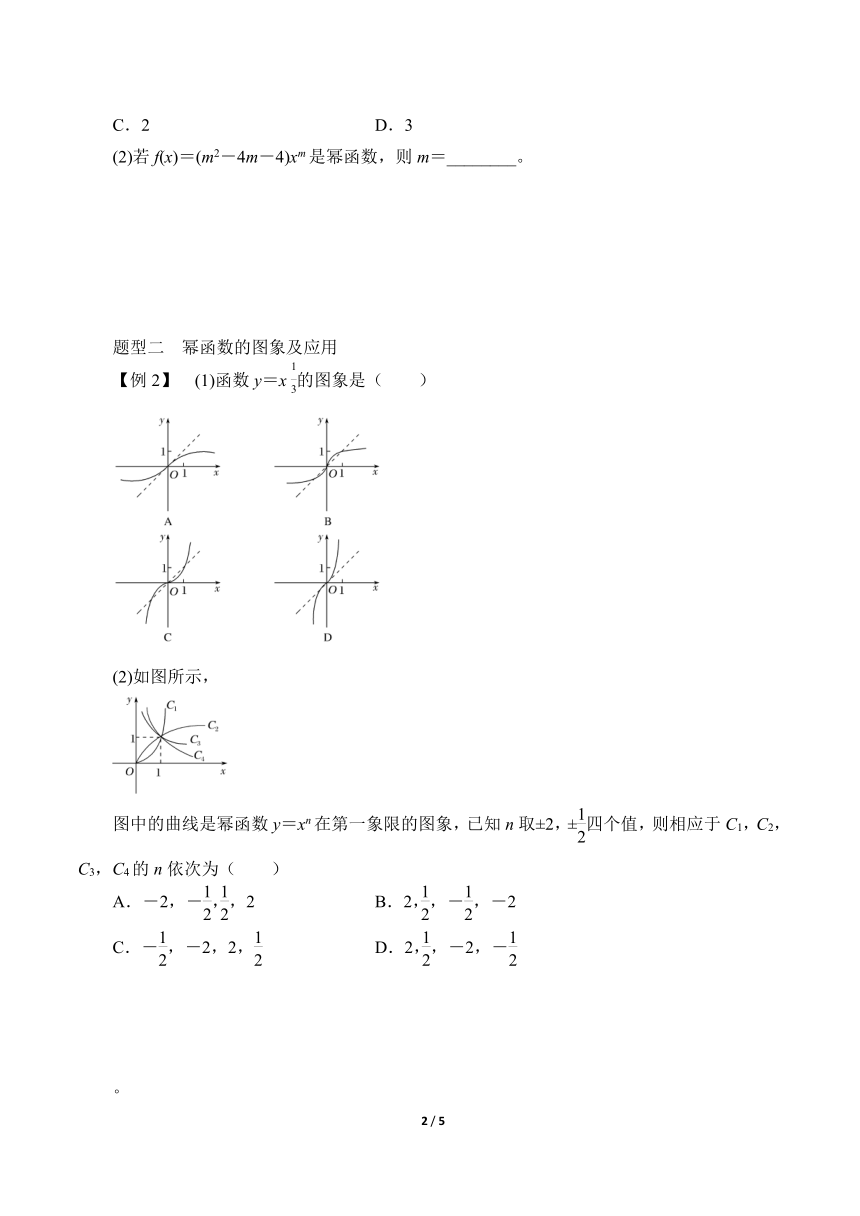
文档简介
幂函数
【学习目标】
1.了解幂函数的概念,会求幂函数的解析式。
2.通过具体实例,结合y=x,y=x2,y=x3,y=x-1,y=x的图象,理解它们的变化规律,了解幂函数。
【学习重难点】
了解幂函数的概念,会求幂函数的解析式。
【学习过程】
一、新知初探
1.幂函数的概念
我们把形如y=xα的函数称为幂函数,其中x是自变量,α是常数。
2.幂函数y=xα的性质
(1)当α>0时,幂函数y=xα具有如下性质:
①函数的图象过点(0,0),(1,1)。
②在第一象限内,函数的图象随x的增大而上升,即函数在区间[0,+∞)上是增函数。
(2)当α<0时,具有的性质为:
①函数的图象都过点(1,1)。
②在第一象限内,函数的图象随x的增大而下降,即函数在区间(0,+∞)上是减函数。
二、初试身手
1.下列所给的函数中是幂函数的为( )
A.y=2x5 B.y=x3+1
C.y=x-3 D.y=3x
2.已知幂函数y=xα的图象经过点(2,4),则f(-3)=________。
3.3.17-1与3.71-1的大小关系为_________________________________________。
三、合作探究
题型一 幂函数的概念
【例1】 (1)在函数y=x-2,y=2x2,y=(x+1)2,y=3x中,幂函数的个数为( )
A.0 B.1
C.2 D.3
(2)若f(x)=(m2-4m-4)xm是幂函数,则m=________。
题型二 幂函数的图象及应用
【例2】 (1)函数y=x的图象是( )
(2)如图所示,
图中的曲线是幂函数y=xn在第一象限的图象,已知n取±2,±四个值,则相应于C1,C2,C3,C4的n依次为( )
A.-2,-,,2 B.2,,-,-2
C.-,-2,2, D.2,,-2,-
。
题型三 由幂函数单调性比较大小
【例3】 比较下列各组数中两个数的大小:
(1)与;
(2)与。
题型四 幂函数性质的综合应用
【例4】 已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称且在(0,+∞)上单调递减,求满足(a+1)-<(3-2a)-的a的取值范围。
【学习小结】
1.结合常见幂函数的图象,归纳幂函数的图象与性质,提升学生的数学抽象素养,逻辑推理素养。
2.幂函数在第一象限内指数变化规律
在第一象限内直线x=1的右侧,图象从上到下,相应的幂的指数由大变小;在直线x=1的左侧,图象从下到上,相应的幂的指数由大变小。
3.简单幂函数的性质
(1)所有幂函数在(0,+∞)上都有定义,并且当自变量为1时,函数值为1,即f(1)=1.恒过点(1,1)。
(2)如果α>0,幂函数在[0,+∞)上有意义,且是增函数。
(3)如果α<0,幂函数在x=0处无意义,在(0,+∞)上是减函数。
4.(1)五个幂函数的图象:
(2)五个幂函数的性质:
幂函数 y=x y=x2 y=x3 y=x y=x-1
定义域 R R R [0,+∞) (-∞,0)∪(0,+∞)
值域 R [0,+∞) R [0,+∞) {y|y∈R,且y≠0}
奇偶性 奇 偶 奇 非奇非偶 奇
单调性 增 x∈[0,+∞),增x∈(-∞,0],减 增 增 x∈(0,+∞),减x∈(-∞,0),减
公共点 都经过点(1,1)
【精炼反馈】
1.设α∈,则使函数y=xα的定义域为R且为奇函数的所有α值为( )
A.1,3 B.-1,1
C.-1,3 D.-1,1,3
2.下列不等式成立的是( )
A.> B.<
C.> D.8-<
3.幂函数y=f(x)的图象过点(2,m),且f(m)=16,则实数m的值为________。
4.函数y=x与函数y=x-1的图象交点坐标为________。
5.若(2a-1)->(3-a)-,求实数a的取值范围。
5 / 5
【学习目标】
1.了解幂函数的概念,会求幂函数的解析式。
2.通过具体实例,结合y=x,y=x2,y=x3,y=x-1,y=x的图象,理解它们的变化规律,了解幂函数。
【学习重难点】
了解幂函数的概念,会求幂函数的解析式。
【学习过程】
一、新知初探
1.幂函数的概念
我们把形如y=xα的函数称为幂函数,其中x是自变量,α是常数。
2.幂函数y=xα的性质
(1)当α>0时,幂函数y=xα具有如下性质:
①函数的图象过点(0,0),(1,1)。
②在第一象限内,函数的图象随x的增大而上升,即函数在区间[0,+∞)上是增函数。
(2)当α<0时,具有的性质为:
①函数的图象都过点(1,1)。
②在第一象限内,函数的图象随x的增大而下降,即函数在区间(0,+∞)上是减函数。
二、初试身手
1.下列所给的函数中是幂函数的为( )
A.y=2x5 B.y=x3+1
C.y=x-3 D.y=3x
2.已知幂函数y=xα的图象经过点(2,4),则f(-3)=________。
3.3.17-1与3.71-1的大小关系为_________________________________________。
三、合作探究
题型一 幂函数的概念
【例1】 (1)在函数y=x-2,y=2x2,y=(x+1)2,y=3x中,幂函数的个数为( )
A.0 B.1
C.2 D.3
(2)若f(x)=(m2-4m-4)xm是幂函数,则m=________。
题型二 幂函数的图象及应用
【例2】 (1)函数y=x的图象是( )
(2)如图所示,
图中的曲线是幂函数y=xn在第一象限的图象,已知n取±2,±四个值,则相应于C1,C2,C3,C4的n依次为( )
A.-2,-,,2 B.2,,-,-2
C.-,-2,2, D.2,,-2,-
。
题型三 由幂函数单调性比较大小
【例3】 比较下列各组数中两个数的大小:
(1)与;
(2)与。
题型四 幂函数性质的综合应用
【例4】 已知幂函数y=x3m-9(m∈N*)的图象关于y轴对称且在(0,+∞)上单调递减,求满足(a+1)-<(3-2a)-的a的取值范围。
【学习小结】
1.结合常见幂函数的图象,归纳幂函数的图象与性质,提升学生的数学抽象素养,逻辑推理素养。
2.幂函数在第一象限内指数变化规律
在第一象限内直线x=1的右侧,图象从上到下,相应的幂的指数由大变小;在直线x=1的左侧,图象从下到上,相应的幂的指数由大变小。
3.简单幂函数的性质
(1)所有幂函数在(0,+∞)上都有定义,并且当自变量为1时,函数值为1,即f(1)=1.恒过点(1,1)。
(2)如果α>0,幂函数在[0,+∞)上有意义,且是增函数。
(3)如果α<0,幂函数在x=0处无意义,在(0,+∞)上是减函数。
4.(1)五个幂函数的图象:
(2)五个幂函数的性质:
幂函数 y=x y=x2 y=x3 y=x y=x-1
定义域 R R R [0,+∞) (-∞,0)∪(0,+∞)
值域 R [0,+∞) R [0,+∞) {y|y∈R,且y≠0}
奇偶性 奇 偶 奇 非奇非偶 奇
单调性 增 x∈[0,+∞),增x∈(-∞,0],减 增 增 x∈(0,+∞),减x∈(-∞,0),减
公共点 都经过点(1,1)
【精炼反馈】
1.设α∈,则使函数y=xα的定义域为R且为奇函数的所有α值为( )
A.1,3 B.-1,1
C.-1,3 D.-1,1,3
2.下列不等式成立的是( )
A.> B.<
C.> D.8-<
3.幂函数y=f(x)的图象过点(2,m),且f(m)=16,则实数m的值为________。
4.函数y=x与函数y=x-1的图象交点坐标为________。
5.若(2a-1)->(3-a)-,求实数a的取值范围。
5 / 5
