北师大版数学九上1.3.1正方形的性质与判定 一课一练(word版含答案)
文档属性
| 名称 | 北师大版数学九上1.3.1正方形的性质与判定 一课一练(word版含答案) | 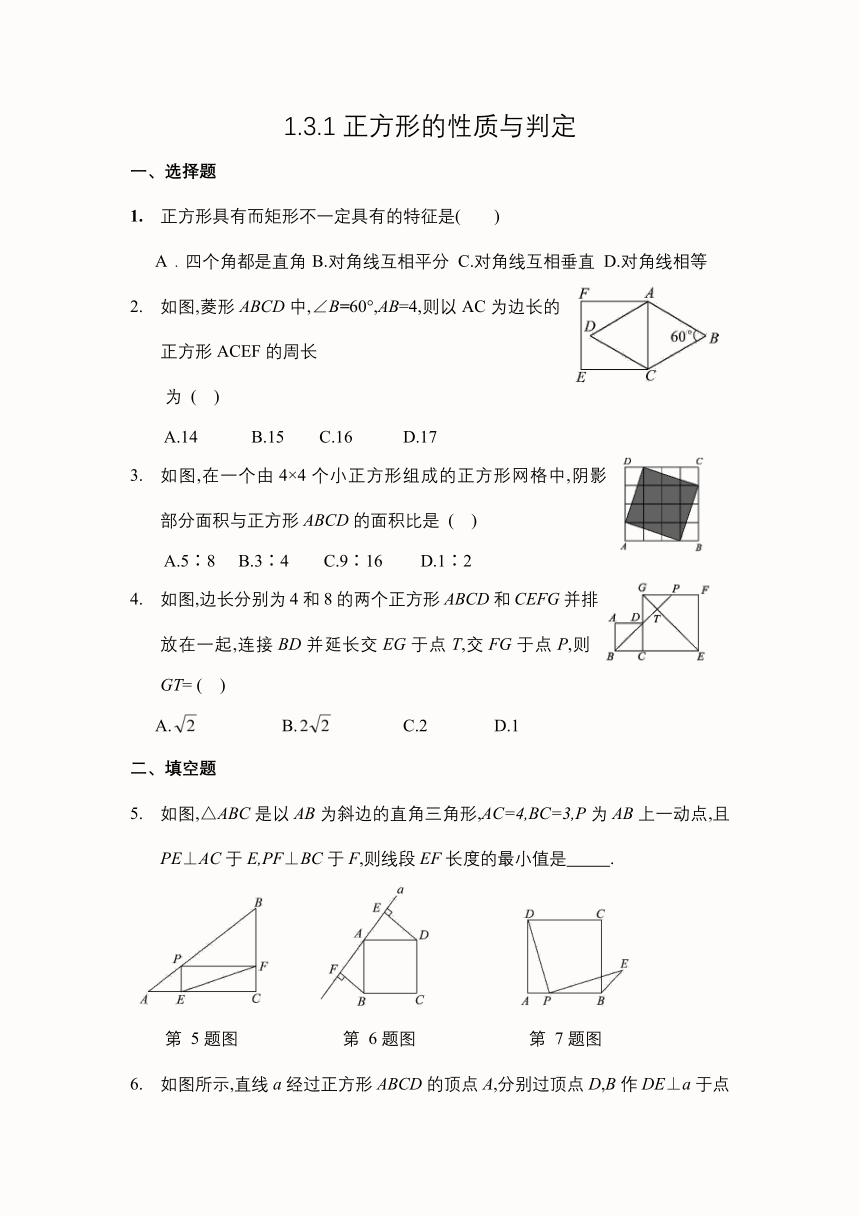 | |
| 格式 | docx | ||
| 文件大小 | 165.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 08:03:52 | ||
图片预览


文档简介
1.3.1正方形的性质与判定
一、选择题
正方形具有而矩形不一定具有的特征是( )
A.四个角都是直角 B.对角线互相平分 C.对角线互相垂直 D.对角线相等
如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长
为 ( )
A.14 B.15 C.16 D.17
如图,在一个由4×4个小正方形组成的正方形网格中,阴影 部分面积与正方形ABCD的面积比是 ( )
A.5∶8 B.3∶4 C.9∶16 D.1∶2
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT= ( )
A. B. C.2 D.1
二、填空题
如图,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为AB上一动点,且PE⊥AC于E,PF⊥BC于F,则线段EF长度的最小值是 .
第 5题图 第 6题图 第 7题图
如图所示,直线a经过正方形ABCD的顶点A,分别过顶点D,B作DE⊥a于点E,BF⊥a于点F,若DE=4,BF=3,则EF的长为 .
点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕
点P顺时针旋转90°得线段PE,连接BE,则∠CBE等于___________.
三、解答题
如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
(1)判断四边形ACED的形状,并说明理由.
(2)若BD=8cm,求线段BE的长.
如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
(1)求证:△BCP≌△DCP.
(2)求证:∠DPE=∠ABC.(3)把正方形ABCD改为菱形,其他条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
10.在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形.把一张正方形纸片按照图①~④的过程折叠后展开.
(1)猜想四边形ABCD是什么四边形.
(2)请证明你所得到的数学猜想.
参考答案
1. C 2. C 3. A 4. B 5. 6. 7 7. 45°
8. (1)四边形ACED是平行四边形.
理由如下:∵四边形ABCD是正方形,
∴AD∥BC,即AD∥CE,
∵DE∥AC,∴四边形ACED是平行四边形.
(2)由(1)知,BC = AD = CE = CD,
在Rt△BCD中,令BC=CD=x,则x2+x2=82.
解得x=4,∴BE=2x=8(cm).
9.(1)在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,
∵在△BCP和△DCP中,
∴△BCP≌△DCP(SAS).
(2)由(1)知,△BCP≌△DCP,
∴∠CBP=∠CDP,
∵PE=PB,∴∠CBP=∠E,∴∠CDP=∠E,
∵∠1=∠2(对顶角相等),
∴180°-∠1-∠CDP=180°-∠2-∠E,
即∠DPE=∠DCE,
∵AB∥CD,∴∠DCE=∠ABC,∴∠DPE=∠ABC.
(3)与(2)同理可得:∠DPE=∠ABC=58°.
10.(1)四边形ABCD是菱形.
(2)∵△AMG沿AG折叠,使AM落在AC上,
∴∠MAD=∠DAC=∠MAC,
同理可得∠CAB=∠NAB=∠CAN,∠DCA=∠MCD
=∠ACM,∠ACB=∠NCB=∠ACN,
∵四边形AMCN是正方形,
∴∠MAC=∠MCA=∠NAC=∠NCA,
∴∠DAC=∠BAC=∠BCA=∠DCA.
∴AD∥BC,AB∥DC,∴四边形ABCD为平行四边形,
∵∠DAC=∠DCA,∴AD=CD,∴四边形ABCD为菱形.
一、选择题
正方形具有而矩形不一定具有的特征是( )
A.四个角都是直角 B.对角线互相平分 C.对角线互相垂直 D.对角线相等
如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长
为 ( )
A.14 B.15 C.16 D.17
如图,在一个由4×4个小正方形组成的正方形网格中,阴影 部分面积与正方形ABCD的面积比是 ( )
A.5∶8 B.3∶4 C.9∶16 D.1∶2
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT= ( )
A. B. C.2 D.1
二、填空题
如图,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为AB上一动点,且PE⊥AC于E,PF⊥BC于F,则线段EF长度的最小值是 .
第 5题图 第 6题图 第 7题图
如图所示,直线a经过正方形ABCD的顶点A,分别过顶点D,B作DE⊥a于点E,BF⊥a于点F,若DE=4,BF=3,则EF的长为 .
点P是正方形ABCD边AB上一点(不与A,B重合),连接PD并将线段PD绕
点P顺时针旋转90°得线段PE,连接BE,则∠CBE等于___________.
三、解答题
如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
(1)判断四边形ACED的形状,并说明理由.
(2)若BD=8cm,求线段BE的长.
如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
(1)求证:△BCP≌△DCP.
(2)求证:∠DPE=∠ABC.(3)把正方形ABCD改为菱形,其他条件不变(如图②),若∠ABC=58°,则∠DPE= 度.
10.在折纸这种传统手工艺术中,蕴含许多数学思想,我们可以通过折纸得到一些特殊图形.把一张正方形纸片按照图①~④的过程折叠后展开.
(1)猜想四边形ABCD是什么四边形.
(2)请证明你所得到的数学猜想.
参考答案
1. C 2. C 3. A 4. B 5. 6. 7 7. 45°
8. (1)四边形ACED是平行四边形.
理由如下:∵四边形ABCD是正方形,
∴AD∥BC,即AD∥CE,
∵DE∥AC,∴四边形ACED是平行四边形.
(2)由(1)知,BC = AD = CE = CD,
在Rt△BCD中,令BC=CD=x,则x2+x2=82.
解得x=4,∴BE=2x=8(cm).
9.(1)在正方形ABCD中,BC=DC,∠BCP=∠DCP=45°,
∵在△BCP和△DCP中,
∴△BCP≌△DCP(SAS).
(2)由(1)知,△BCP≌△DCP,
∴∠CBP=∠CDP,
∵PE=PB,∴∠CBP=∠E,∴∠CDP=∠E,
∵∠1=∠2(对顶角相等),
∴180°-∠1-∠CDP=180°-∠2-∠E,
即∠DPE=∠DCE,
∵AB∥CD,∴∠DCE=∠ABC,∴∠DPE=∠ABC.
(3)与(2)同理可得:∠DPE=∠ABC=58°.
10.(1)四边形ABCD是菱形.
(2)∵△AMG沿AG折叠,使AM落在AC上,
∴∠MAD=∠DAC=∠MAC,
同理可得∠CAB=∠NAB=∠CAN,∠DCA=∠MCD
=∠ACM,∠ACB=∠NCB=∠ACN,
∵四边形AMCN是正方形,
∴∠MAC=∠MCA=∠NAC=∠NCA,
∴∠DAC=∠BAC=∠BCA=∠DCA.
∴AD∥BC,AB∥DC,∴四边形ABCD为平行四边形,
∵∠DAC=∠DCA,∴AD=CD,∴四边形ABCD为菱形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
