人教版数学八年级下册19.1.2 函数的图象(含2课时)教案
文档属性
| 名称 | 人教版数学八年级下册19.1.2 函数的图象(含2课时)教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 14:35:02 | ||
图片预览



文档简介
19.1.2 函数的图象
第1课时 函数图象
1.学会用列表、描点、连线画函数图象.
2.学会观察、分析函数图象信息.
自学指导:阅读教材75页至77页,独立完成下列问题:
知识探究(一)
(1)已知函数y=x+1,按要求完成以下步骤:
①当x=-3,x=-2,x=-1,x=0,x=1,x=2,x=3时,求出对应的y的值;
②将每一对值都写成(x,y)这的形式,当作一个点的坐标,在直角坐标系中描出这些点,并将它们依次连接起来;
③指出描出的图象的形状.
(2)归纳①:一般地,对于一个函数,如果把自变量与函数的每对对应值分别做为点的横、纵坐标,那么平面内由这些点组成的图形,就是这个函数的图象.
归纳②:当函数图象从左向右上升时,函数值随自变量由小变大而由小变大;当图象从左向右下降时,函数值随自变量由小变大而由大变小.
明确已知自变量和函数值中的任意一个量可根据解析式求出另一个量,同时可在坐标系中找到与之对应的点,如果已知函数的图象上的某一点的横纵坐标,代入解析式两边可使等式成立.
自学反馈
(1)下列各点在函数y=x+2的图象上的有A、B、C、D.
A.(1,3) B.(-2,0) C.(4.1,6.1) D.(-6,-4) E.(-5,3)
(2)蜡是非晶体,在加热过程中先要变软,然后逐渐变稀,然后全部变为液态,整个过程温度不断上升,没有一定的熔化温度,如下图所示,四个图象中表示蜡熔化的是( C )
可用排除法,应该温度不断上升,可排除B、D,而A的图象显示温度有一断时间出现恒定不变,与题意不符,故排除.
自学指导:阅读教材77页至79页,独立完成下列问题:
知识探究(二)
描点法画函数图象的一般步骤:(1)列表;(2)描点;(3)连线.
活动1 学生独立完成
例1 一位旅行者在早晨8点从城市出发到乡村,第一小时走了5千米,然后他上坡,1小时走了3千米,以后就休息30分钟;休息后平均每小时走4千米,在中午12时到达乡村,他离开城市的距离s跟出发的时间之间的函数关系如图所示,根据图回答:
(1)旅行到9时、10时30分、11时离开城市的距离分别为多少;
(2)他停下来休息时,离开城市的距离是多少;
(3)乡村离城市有多少千米路程;
(4)旅行者离开城市6千米、10千米、12千米、14千米的时间分别为多少.
解:(1)距离分别为5千米、8千米、10千米;
(2)停下休息时,离开城市的距离是8千米;
(3)乡村离城市有14千米路程;
(4)时间分别为9点20分,11点,11点半,12点.
通过此题的训练使学生熟练掌握通过函数图象,结合题目所给信息解决实际问题,此类题首先要弄清楚横纵轴分别表示什么实际意义,再结合图象弄清楚每段图象分别表示的实际意义.
例2 作出函数y=-的图象.
解:(1)列表.
x -6 -4 -3 -2 -1 1 2 3 4 6
y 1 1.5 2 3 6 -6 -3 -2 -1.5 -1
(2)描点、连线,如图.
画函数图象要经列表、描点、连线三个步骤,列表时自变量取值要有代表性(自变量不可以只取正数,也不可以只取负数),自变量不为0,表示图象不是连续的,在自变量为0时,图象断开,分为两段.
活动2 跟踪训练
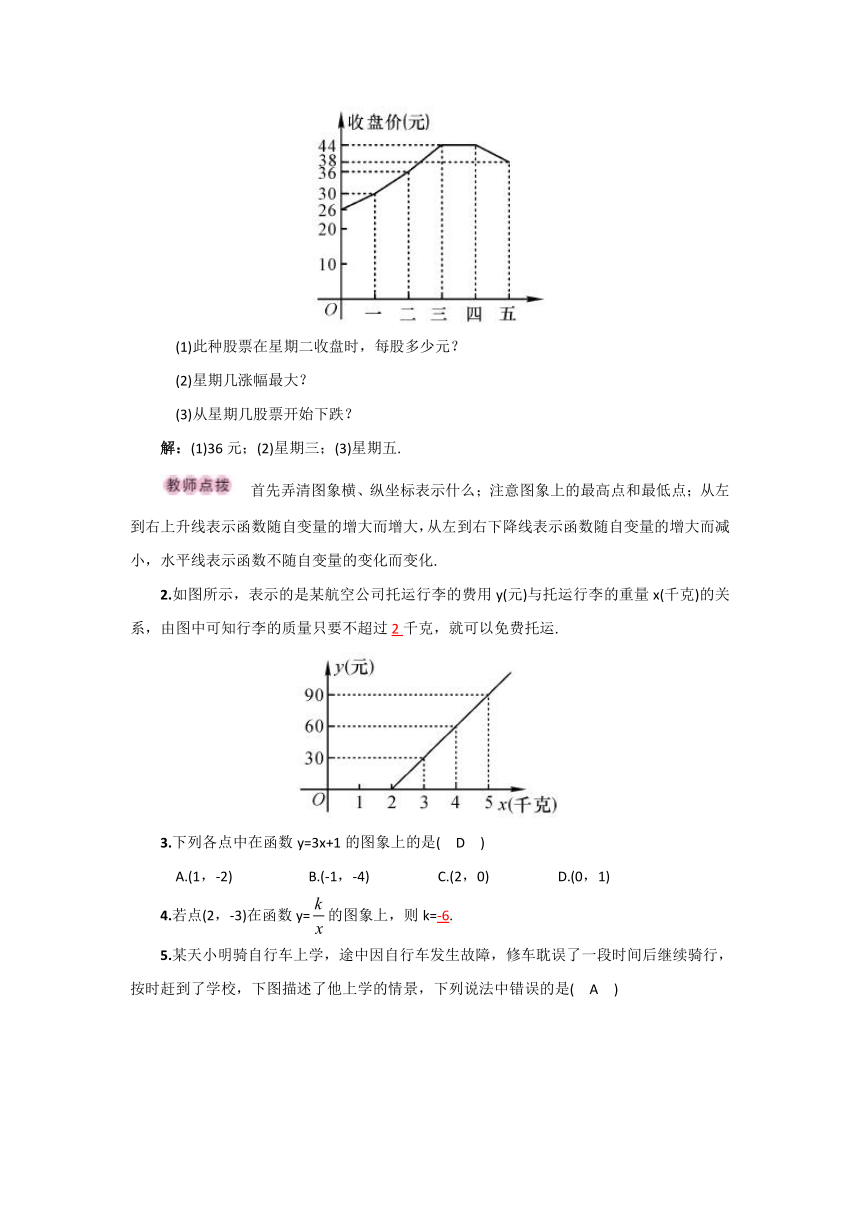
1.某证券交易所提供的某种股票一周内的涨跌的情况如图所示,根据图象回答下列问题:
(1)此种股票在星期二收盘时,每股多少元?
(2)星期几涨幅最大?
(3)从星期几股票开始下跌?
解:(1)36元;(2)星期三;(3)星期五.
首先弄清图象横、纵坐标表示什么;注意图象上的最高点和最低点;从左到右上升线表示函数随自变量的增大而增大,从左到右下降线表示函数随自变量的增大而减小,水平线表示函数不随自变量的变化而变化.
2.如图所示,表示的是某航空公司托运行李的费用y(元)与托运行李的重量x(千克)的关系,由图中可知行李的质量只要不超过2千克,就可以免费托运.
3.下列各点中在函数y=3x+1的图象上的是( D )
A.(1,-2) B.(-1,-4) C.(2,0) D.(0,1)
4.若点(2,-3)在函数y=的图象上,则k=-6.
5.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,下图描述了他上学的情景,下列说法中错误的是( A )
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
6.甲、乙两人在一次赛跑中,路程与时间的关系如图所示,由图可以知道:
(1)这是一次100米赛跑;
(2)甲、乙两人先到达终点的是甲;
(3)在这次赛跑中甲的速度为米/秒,乙的速度为8米/秒.
7.已知函数y=2x-1.
(1)试判断点A(-1,3)和点B(,-)是否在此函数的图象上;
(2)已知点(a,a+1)在此函数图象上,求a的值.
解:(1)A点不在,B点在;(2)a=2.
判断点是否在函数的图象上,就是把横纵坐标分别代入表达式的左右两边看等式是否成立.
8.下列各曲线中哪些表示y是x的函数?
解:①,②,③.
在x轴上任取一点,看与之对应的y值,如果是唯一的,就是函数关系,反之则不是,多取几点.(可在x轴上取一点做x轴的垂线,看它与图象的交点)
活动3 课堂小结
学生尝试小结:这节课你学到了什么
第2课时 函数表示方法
1.总结函数三种表示方法,了解三种表示方法的优缺点.
2.会根据具体情况选择适当方法.
自学指导:阅读教材79页至81页,独立完成下列问题:
知识探究
(1)函数的表示方法:解析式法、图象法、列表法.
(2)三种函数表示方法的优缺点:
①列表法能明显地显示出自变量与其对应的函数值,但具有局限性;
②图象法形象直观,但画出的图象是近似的局部的,往往不够准确;
③解析法的优点是简单明了,但它在求对应值时,往往需要复杂的计算才能得出.
自学反馈
(1)用列表法与解析式法表示n边形的内角和m(单位:度)是边数n的函数;
(2)用解析式法与图象法表示等边三角形的周长l是边长a的函数.
列表法时要注意所取值要有一定的代表性,一般取整数点,便于描点画图.
活动1 学生独立完成
例1 已知等腰三角形的周长为12cm,若底边长为ycm,一腰长为xcm.
(1)确定y与x之间的函数关系式;
(2)确定x的取值范围;
(3)画出函数的图象.
解:(1)依题意,得y=12-2x.
(2)∵∴
∴自变量x的取值范围是3<x<6.
(3)列表:
x 3 4 5 5.5 6
y 6 4 2 1 0
描点、连线,其图象如图所示.
根据等腰三角形的周长确定底边长y与腰长x间的函数关系式;在确定自变量的取值范围时,注意两腰长之和小于周长,组成三角形要保证底边长小于两腰之和;画函数图象分三个步骤进行,在描点时要注意空心圆圈和实心圈点的区别.
例2 下列各点中哪些在函数y=2x-3的图象上?
A.(1,-2) B.(-2.5,-8) C.(0,-2) D.(101,99)
解:点B在该函数图象上.
平面上的点,若横、纵坐标满足函数的解析式,则这个点就在这个函数的图象上.
活动2 跟踪训练
1.一辆汽车与一辆摩托车分别从A、B两地去同一城市,它们离A地的路程随时间变化的图象如图所示,则下列结论错误的是( C )
A.摩托车比汽车晚到1h
B.A、B两地的路程为20km
C.摩托车的速度为45km/h
D.汽车的速度为60km/h
弄清楚横纵轴分别表示的量,图象上的点分别表示的实际意义.
2.某消防水池蓄水900m3,一次消防演习时每分钟抽水15m3去灭火,抽水时间为t(分),池中的剩余水量为V(m3).
(1)写出剩余水量V与时间t的函数关系式;
(2)写出自变量t的取值范围;
(3)画出此函数的图象;
(4)火被扑灭,演习结束,这时池中还有水525m3,这次演习抽水灭火用了多少分钟?
解:(1)V=-15t+900;(2)0≤t≤60;(3)略;(4)25分钟.
根据消防池中的剩余水量等于原有水量减去抽出水量建立函数关系式,抽水时间t与剩余水量V都是非负数,可确定t的取值范围.
3.y=ax+b的图象过点(0,-2)和点(1,1),求这个函数的解析式.
解:y=3x-2.
活动3 课堂小结
1.通过函数的解析式列表,画出图象,根据图表读出其中的信息来解决实际问题,体现了数学中的一个重要思想方法——数形结合思想.
2.平面上的点,若横、纵坐标满足函数的解析式,则这个点就在这个函数的图象上,否则就不在函数的图象上.
第1课时 函数图象
1.学会用列表、描点、连线画函数图象.
2.学会观察、分析函数图象信息.
自学指导:阅读教材75页至77页,独立完成下列问题:
知识探究(一)
(1)已知函数y=x+1,按要求完成以下步骤:
①当x=-3,x=-2,x=-1,x=0,x=1,x=2,x=3时,求出对应的y的值;
②将每一对值都写成(x,y)这的形式,当作一个点的坐标,在直角坐标系中描出这些点,并将它们依次连接起来;
③指出描出的图象的形状.
(2)归纳①:一般地,对于一个函数,如果把自变量与函数的每对对应值分别做为点的横、纵坐标,那么平面内由这些点组成的图形,就是这个函数的图象.
归纳②:当函数图象从左向右上升时,函数值随自变量由小变大而由小变大;当图象从左向右下降时,函数值随自变量由小变大而由大变小.
明确已知自变量和函数值中的任意一个量可根据解析式求出另一个量,同时可在坐标系中找到与之对应的点,如果已知函数的图象上的某一点的横纵坐标,代入解析式两边可使等式成立.
自学反馈
(1)下列各点在函数y=x+2的图象上的有A、B、C、D.
A.(1,3) B.(-2,0) C.(4.1,6.1) D.(-6,-4) E.(-5,3)
(2)蜡是非晶体,在加热过程中先要变软,然后逐渐变稀,然后全部变为液态,整个过程温度不断上升,没有一定的熔化温度,如下图所示,四个图象中表示蜡熔化的是( C )
可用排除法,应该温度不断上升,可排除B、D,而A的图象显示温度有一断时间出现恒定不变,与题意不符,故排除.
自学指导:阅读教材77页至79页,独立完成下列问题:
知识探究(二)
描点法画函数图象的一般步骤:(1)列表;(2)描点;(3)连线.
活动1 学生独立完成
例1 一位旅行者在早晨8点从城市出发到乡村,第一小时走了5千米,然后他上坡,1小时走了3千米,以后就休息30分钟;休息后平均每小时走4千米,在中午12时到达乡村,他离开城市的距离s跟出发的时间之间的函数关系如图所示,根据图回答:
(1)旅行到9时、10时30分、11时离开城市的距离分别为多少;
(2)他停下来休息时,离开城市的距离是多少;
(3)乡村离城市有多少千米路程;
(4)旅行者离开城市6千米、10千米、12千米、14千米的时间分别为多少.
解:(1)距离分别为5千米、8千米、10千米;
(2)停下休息时,离开城市的距离是8千米;
(3)乡村离城市有14千米路程;
(4)时间分别为9点20分,11点,11点半,12点.
通过此题的训练使学生熟练掌握通过函数图象,结合题目所给信息解决实际问题,此类题首先要弄清楚横纵轴分别表示什么实际意义,再结合图象弄清楚每段图象分别表示的实际意义.
例2 作出函数y=-的图象.
解:(1)列表.
x -6 -4 -3 -2 -1 1 2 3 4 6
y 1 1.5 2 3 6 -6 -3 -2 -1.5 -1
(2)描点、连线,如图.
画函数图象要经列表、描点、连线三个步骤,列表时自变量取值要有代表性(自变量不可以只取正数,也不可以只取负数),自变量不为0,表示图象不是连续的,在自变量为0时,图象断开,分为两段.
活动2 跟踪训练
1.某证券交易所提供的某种股票一周内的涨跌的情况如图所示,根据图象回答下列问题:
(1)此种股票在星期二收盘时,每股多少元?
(2)星期几涨幅最大?
(3)从星期几股票开始下跌?
解:(1)36元;(2)星期三;(3)星期五.
首先弄清图象横、纵坐标表示什么;注意图象上的最高点和最低点;从左到右上升线表示函数随自变量的增大而增大,从左到右下降线表示函数随自变量的增大而减小,水平线表示函数不随自变量的变化而变化.
2.如图所示,表示的是某航空公司托运行李的费用y(元)与托运行李的重量x(千克)的关系,由图中可知行李的质量只要不超过2千克,就可以免费托运.
3.下列各点中在函数y=3x+1的图象上的是( D )
A.(1,-2) B.(-1,-4) C.(2,0) D.(0,1)
4.若点(2,-3)在函数y=的图象上,则k=-6.
5.某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,下图描述了他上学的情景,下列说法中错误的是( A )
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
6.甲、乙两人在一次赛跑中,路程与时间的关系如图所示,由图可以知道:
(1)这是一次100米赛跑;
(2)甲、乙两人先到达终点的是甲;
(3)在这次赛跑中甲的速度为米/秒,乙的速度为8米/秒.
7.已知函数y=2x-1.
(1)试判断点A(-1,3)和点B(,-)是否在此函数的图象上;
(2)已知点(a,a+1)在此函数图象上,求a的值.
解:(1)A点不在,B点在;(2)a=2.
判断点是否在函数的图象上,就是把横纵坐标分别代入表达式的左右两边看等式是否成立.
8.下列各曲线中哪些表示y是x的函数?
解:①,②,③.
在x轴上任取一点,看与之对应的y值,如果是唯一的,就是函数关系,反之则不是,多取几点.(可在x轴上取一点做x轴的垂线,看它与图象的交点)
活动3 课堂小结
学生尝试小结:这节课你学到了什么
第2课时 函数表示方法
1.总结函数三种表示方法,了解三种表示方法的优缺点.
2.会根据具体情况选择适当方法.
自学指导:阅读教材79页至81页,独立完成下列问题:
知识探究
(1)函数的表示方法:解析式法、图象法、列表法.
(2)三种函数表示方法的优缺点:
①列表法能明显地显示出自变量与其对应的函数值,但具有局限性;
②图象法形象直观,但画出的图象是近似的局部的,往往不够准确;
③解析法的优点是简单明了,但它在求对应值时,往往需要复杂的计算才能得出.
自学反馈
(1)用列表法与解析式法表示n边形的内角和m(单位:度)是边数n的函数;
(2)用解析式法与图象法表示等边三角形的周长l是边长a的函数.
列表法时要注意所取值要有一定的代表性,一般取整数点,便于描点画图.
活动1 学生独立完成
例1 已知等腰三角形的周长为12cm,若底边长为ycm,一腰长为xcm.
(1)确定y与x之间的函数关系式;
(2)确定x的取值范围;
(3)画出函数的图象.
解:(1)依题意,得y=12-2x.
(2)∵∴
∴自变量x的取值范围是3<x<6.
(3)列表:
x 3 4 5 5.5 6
y 6 4 2 1 0
描点、连线,其图象如图所示.
根据等腰三角形的周长确定底边长y与腰长x间的函数关系式;在确定自变量的取值范围时,注意两腰长之和小于周长,组成三角形要保证底边长小于两腰之和;画函数图象分三个步骤进行,在描点时要注意空心圆圈和实心圈点的区别.
例2 下列各点中哪些在函数y=2x-3的图象上?
A.(1,-2) B.(-2.5,-8) C.(0,-2) D.(101,99)
解:点B在该函数图象上.
平面上的点,若横、纵坐标满足函数的解析式,则这个点就在这个函数的图象上.
活动2 跟踪训练
1.一辆汽车与一辆摩托车分别从A、B两地去同一城市,它们离A地的路程随时间变化的图象如图所示,则下列结论错误的是( C )
A.摩托车比汽车晚到1h
B.A、B两地的路程为20km
C.摩托车的速度为45km/h
D.汽车的速度为60km/h
弄清楚横纵轴分别表示的量,图象上的点分别表示的实际意义.
2.某消防水池蓄水900m3,一次消防演习时每分钟抽水15m3去灭火,抽水时间为t(分),池中的剩余水量为V(m3).
(1)写出剩余水量V与时间t的函数关系式;
(2)写出自变量t的取值范围;
(3)画出此函数的图象;
(4)火被扑灭,演习结束,这时池中还有水525m3,这次演习抽水灭火用了多少分钟?
解:(1)V=-15t+900;(2)0≤t≤60;(3)略;(4)25分钟.
根据消防池中的剩余水量等于原有水量减去抽出水量建立函数关系式,抽水时间t与剩余水量V都是非负数,可确定t的取值范围.
3.y=ax+b的图象过点(0,-2)和点(1,1),求这个函数的解析式.
解:y=3x-2.
活动3 课堂小结
1.通过函数的解析式列表,画出图象,根据图表读出其中的信息来解决实际问题,体现了数学中的一个重要思想方法——数形结合思想.
2.平面上的点,若横、纵坐标满足函数的解析式,则这个点就在这个函数的图象上,否则就不在函数的图象上.
