人教版七年级下册6.1 平方根课件(共45张PPT)
文档属性
| 名称 | 人教版七年级下册6.1 平方根课件(共45张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 10:23:46 | ||
图片预览









文档简介
(共46张PPT)
R·七年级下册
第3课时 平方根
学习目标:
(1)知道什么叫平方根?用符号如何表示它?有哪些性质?
(2)能利用开平方与平方互为逆运算求某些非负数的平方根.
学习重、难点:
重点:平方根的概念.
难点:平方根与算术平方根的区别和联系.
情景导入
思考
如果一个数的平方等于9,这个数是多少?
探究新知
知识点1
平方根的概念
3的平方是9. 除了3之外,还有没有别的数的平方也等于9呢?
如果一个数的平方等于9,这个数是多少?
( –3 )2 = 9
这个数也可以是 – 3.
因此这个数是3或– 3.
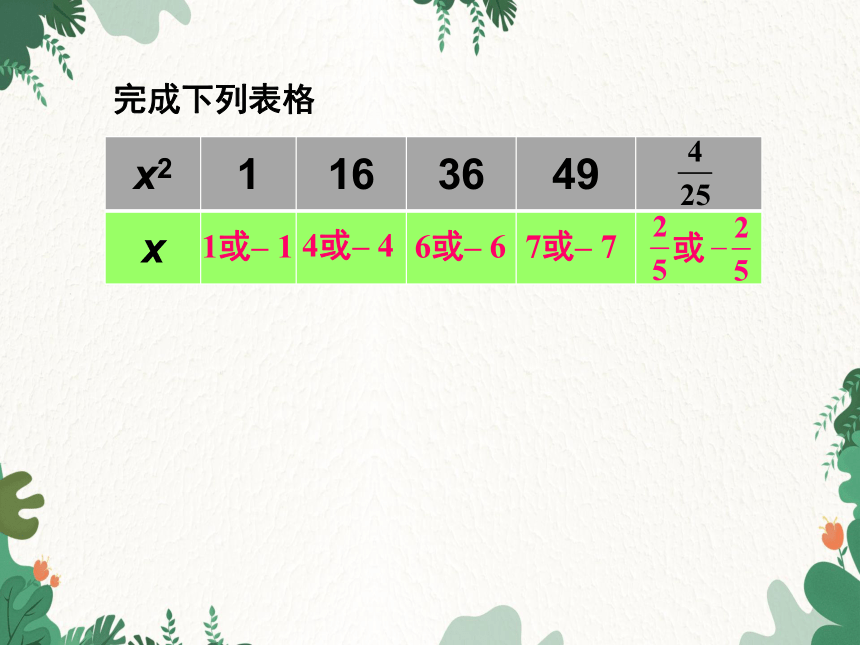
x2 1 16 36 49
x
完成下列表格
1或– 1
4或– 4
6或– 6
7或– 7
或
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.
这就是说x2 = a,那么x叫做a的平方根.
求一个数a的平方根的运算,叫做开平方.
例如 ±3的平方等于9
3和 – 3是9的平方根,简记为±3是9的平方根.
我们看到,±3的平方等于9,9的平方根是±3,所以平方与开平方互为逆运算.
– 1
+ 1
+ 2
– 2
+ 3
– 3
1
4
9
– 1
+ 1
+ 2
– 2
+ 3
– 3
1
4
9
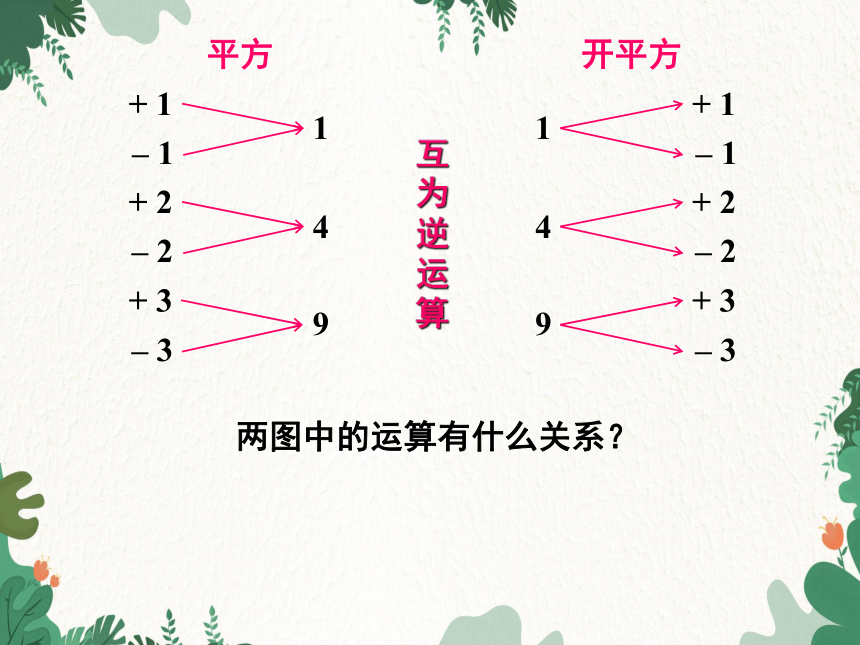
平方
开平方
两图中的运算有什么关系?
互为逆运算
例4 求下列各数的平方根:
(1)100 (2) (3)0.25
解:(1)因为(±10)2 = 100,
所以100的平方根是 ±10;
(2)因为(± )2 = ,
所以 的平方根是 ± ;
(3)因为(±0.5)2 = 0.25,
所以0.25的平方根是 ±0.5;
练习
1.求下列各数的平方根.
25
0.64
(– 2)4
±5
±0.8
±4
±3
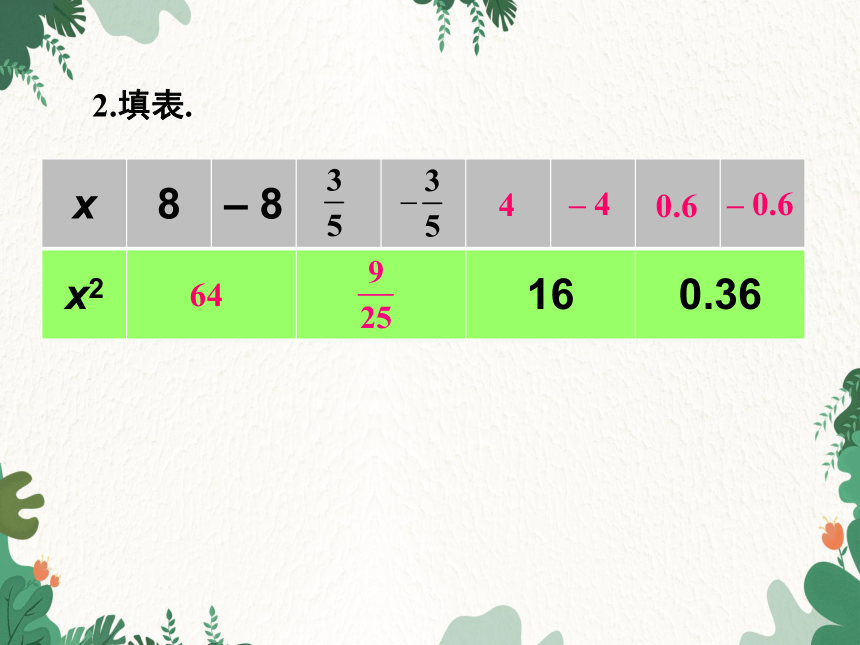
2.填表.
x 8 – 8
x2 16 0.36
64
4
– 4
– 0.6
0.6
知识点2
平方根的性质
思考
正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根.
因为02 = 0,并且任何一个不为0的数的平方都不等于0,所以0的平方根是0.
正数的平方是正数,0的平方是0,负数的平方也是正数,即在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根.
结
论
正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
正数a的算术平方根可以用 表示;
正数a的负的平方根,可以用符号 表示;
正数a的平方根用符号 表示.读作“正、负根号a ”.
符号 只有当a ≥ 0 时才有意义。a < 0 时无意义.
例5 求下列各式的值:
(1)
(2)
(3)
解:(1)因为62 = 36,所以 = 6;
(2)因为0.92 = 0.81,所以 = – 0.9;
(3)因为( )2 = ,所以 = .
如果知道一个数的算术平方根就可以立即写出它的负的平方根,为什么?
因为正数的两个平方根互为相反数.
练习
1.判断下列说法是否正确.
(1)0的平方根是0; ( )
(2)1的平方根是1; ( )
(3)– 1的平方根是– 1; ( )
(4)0.1是0.01的一个平方根. ( )
√
√
×
×
2.计算下列各式的值:
(1)
(2)
(3)
= 3
= – 0.7
3.平方根概念的起源与几何中的正方形有关. 如果一个正方形的面积为A ,那么这个正方形的边长是多少?
解:边长为
误
区
诊
断
误区:对± , ,– 辨识不清而致错
例1 求下列各式的值:(1) (2)–
错解:(1)因为(±4)2=16,所以 =±4;
(2)因为(±5)2=25,所以– =±5;
正解:(1)因为 表示16的算术平方根,所以 =4.
(2)因为– 表示25的负算术平方根,所以
– = –5.
错因分析:此题错解在于没有弄清± ,
,– 的意义 ,他们分别表示a的平方根,a的算术平方根,a的负的平方根,解题时,
“ ”的前面是什么符号,对计算结果是有影响的.
基础巩固
随堂演练
1. 下列各式:① ;② ;③ ;④ 中,有意义的有( )
A.1个 B.2个 C.3个 D.4个
C
2. 下列各式中正确的是( )
A. = – 2 B. = – 5
C. =5 D. =±4
C
3. 下列说法中正确的有( )
(1)0的平方根是0;(2)1的平方根是1;
(3)– 1的平方根是– 1;(4)±0.01是0.1的平方根
A.1个 B.2个 C.3个 D.4个
A
综合运用
4. 求下列各式中x的值:
(1)x2 = 25;(2)x2 – 81 = 0;(3)25x2 = 36.
解:(1)∵(±5)2 = 25,∴x = ±5;
(2)∵(±9)2 = 81,∴x = ±9;
(3)x2 = .∵( ± )2 = .
∴x = ± .
5.根据下表回答下列问题:
x 16 16.1 16.2 16.3 16.4 16.5
x2 256 259.21 262.44 265.69 268.96 272.25
x 16.6 16.7 16.8 16.9 17
x2 275.56 278.89 282.24 285.61 289
(1)268.96的平方根是________;
(2) ≈______;
(3) 在表中哪两个相邻的数之间?为什么?
解: 在表中16.4和16.5这两个相邻的数之间.
∵268.96 < 270 < 272.25,
∴16.4 < < 16.5.
±16.4
16.9
课堂小结
结
论
正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
伸
延
展
拓
若一个数x的平方根是2a+3和1 – 4a,求a和x的值.
解:∵2a+3和1 – 4a是x的平方根,
∴2a+3+1 – 4a=0,
∴a = 2,
∴2a+3 = 2×2+3 = 7.
∴x =(2a+3)2 = 72 = 49.
1. 从课后习题中选取;
2. 完成练习册本课时的习题。
课后作业
教学反思
本课时教学重在挖掘平方根与算术平方根间的区别与联系,通过实例训练引导学生认识新知识,形成计算能力.
习题6.1
复习巩固
综合运用
拓广探索
R·七年级下册
第3课时 平方根
学习目标:
(1)知道什么叫平方根?用符号如何表示它?有哪些性质?
(2)能利用开平方与平方互为逆运算求某些非负数的平方根.
学习重、难点:
重点:平方根的概念.
难点:平方根与算术平方根的区别和联系.
情景导入
思考
如果一个数的平方等于9,这个数是多少?
探究新知
知识点1
平方根的概念
3的平方是9. 除了3之外,还有没有别的数的平方也等于9呢?
如果一个数的平方等于9,这个数是多少?
( –3 )2 = 9
这个数也可以是 – 3.
因此这个数是3或– 3.
x2 1 16 36 49
x
完成下列表格
1或– 1
4或– 4
6或– 6
7或– 7
或
一般地,如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.
这就是说x2 = a,那么x叫做a的平方根.
求一个数a的平方根的运算,叫做开平方.
例如 ±3的平方等于9
3和 – 3是9的平方根,简记为±3是9的平方根.
我们看到,±3的平方等于9,9的平方根是±3,所以平方与开平方互为逆运算.
– 1
+ 1
+ 2
– 2
+ 3
– 3
1
4
9
– 1
+ 1
+ 2
– 2
+ 3
– 3
1
4
9
平方
开平方
两图中的运算有什么关系?
互为逆运算
例4 求下列各数的平方根:
(1)100 (2) (3)0.25
解:(1)因为(±10)2 = 100,
所以100的平方根是 ±10;
(2)因为(± )2 = ,
所以 的平方根是 ± ;
(3)因为(±0.5)2 = 0.25,
所以0.25的平方根是 ±0.5;
练习
1.求下列各数的平方根.
25
0.64
(– 2)4
±5
±0.8
±4
±3
2.填表.
x 8 – 8
x2 16 0.36
64
4
– 4
– 0.6
0.6
知识点2
平方根的性质
思考
正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根.
因为02 = 0,并且任何一个不为0的数的平方都不等于0,所以0的平方根是0.
正数的平方是正数,0的平方是0,负数的平方也是正数,即在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根.
结
论
正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
正数a的算术平方根可以用 表示;
正数a的负的平方根,可以用符号 表示;
正数a的平方根用符号 表示.读作“正、负根号a ”.
符号 只有当a ≥ 0 时才有意义。a < 0 时无意义.
例5 求下列各式的值:
(1)
(2)
(3)
解:(1)因为62 = 36,所以 = 6;
(2)因为0.92 = 0.81,所以 = – 0.9;
(3)因为( )2 = ,所以 = .
如果知道一个数的算术平方根就可以立即写出它的负的平方根,为什么?
因为正数的两个平方根互为相反数.
练习
1.判断下列说法是否正确.
(1)0的平方根是0; ( )
(2)1的平方根是1; ( )
(3)– 1的平方根是– 1; ( )
(4)0.1是0.01的一个平方根. ( )
√
√
×
×
2.计算下列各式的值:
(1)
(2)
(3)
= 3
= – 0.7
3.平方根概念的起源与几何中的正方形有关. 如果一个正方形的面积为A ,那么这个正方形的边长是多少?
解:边长为
误
区
诊
断
误区:对± , ,– 辨识不清而致错
例1 求下列各式的值:(1) (2)–
错解:(1)因为(±4)2=16,所以 =±4;
(2)因为(±5)2=25,所以– =±5;
正解:(1)因为 表示16的算术平方根,所以 =4.
(2)因为– 表示25的负算术平方根,所以
– = –5.
错因分析:此题错解在于没有弄清± ,
,– 的意义 ,他们分别表示a的平方根,a的算术平方根,a的负的平方根,解题时,
“ ”的前面是什么符号,对计算结果是有影响的.
基础巩固
随堂演练
1. 下列各式:① ;② ;③ ;④ 中,有意义的有( )
A.1个 B.2个 C.3个 D.4个
C
2. 下列各式中正确的是( )
A. = – 2 B. = – 5
C. =5 D. =±4
C
3. 下列说法中正确的有( )
(1)0的平方根是0;(2)1的平方根是1;
(3)– 1的平方根是– 1;(4)±0.01是0.1的平方根
A.1个 B.2个 C.3个 D.4个
A
综合运用
4. 求下列各式中x的值:
(1)x2 = 25;(2)x2 – 81 = 0;(3)25x2 = 36.
解:(1)∵(±5)2 = 25,∴x = ±5;
(2)∵(±9)2 = 81,∴x = ±9;
(3)x2 = .∵( ± )2 = .
∴x = ± .
5.根据下表回答下列问题:
x 16 16.1 16.2 16.3 16.4 16.5
x2 256 259.21 262.44 265.69 268.96 272.25
x 16.6 16.7 16.8 16.9 17
x2 275.56 278.89 282.24 285.61 289
(1)268.96的平方根是________;
(2) ≈______;
(3) 在表中哪两个相邻的数之间?为什么?
解: 在表中16.4和16.5这两个相邻的数之间.
∵268.96 < 270 < 272.25,
∴16.4 < < 16.5.
±16.4
16.9
课堂小结
结
论
正数有两个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根.
伸
延
展
拓
若一个数x的平方根是2a+3和1 – 4a,求a和x的值.
解:∵2a+3和1 – 4a是x的平方根,
∴2a+3+1 – 4a=0,
∴a = 2,
∴2a+3 = 2×2+3 = 7.
∴x =(2a+3)2 = 72 = 49.
1. 从课后习题中选取;
2. 完成练习册本课时的习题。
课后作业
教学反思
本课时教学重在挖掘平方根与算术平方根间的区别与联系,通过实例训练引导学生认识新知识,形成计算能力.
习题6.1
复习巩固
综合运用
拓广探索
