5.1.1数据的收集 课件(共121张PPT)
文档属性
| 名称 | 5.1.1数据的收集 课件(共121张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 15:04:24 | ||
图片预览











文档简介
(共121张PPT)
数据的收集
第1课时 总体与样本及简单随机抽样
1.统计的相关概念
总体 所考察问题涉及的对象全体是总体
个体 总体中每个对象都是个体。
样本 抽取的部分对象组成总体的一个样本
样本 容量 一个样本中包含的个体数目是样本容量
2.普查与抽样调查
一般地,对总体中每个个体都进行考察的方法称为普查(也称全面调查),只抽取样本进行考察的方法称为抽样调查。
3.简单随机抽样
(1)定义:一般地,简单随机抽样(也称纯随机抽样)就是从总体中不加任何分组、划类、排队等,完全随机地抽取个体。
(2)两种常见方法:①抽签法;②随机数表法。
【思考】
抽签法与随机数表法的异同点是什么?
提示:
抽签法 随机数表法
不同点 ①抽签法比随机数表法简单;②抽签法适用于总体中的个体数相对较少的情况 ①随机数表法要求编号的位数相同;②随机数表法适用于总体中的个体数相对较多的情况
相同点 ①都是简单随机抽样,并且要求被抽取样本的总体的个数有限;②都是从总体中逐个不放回地抽取
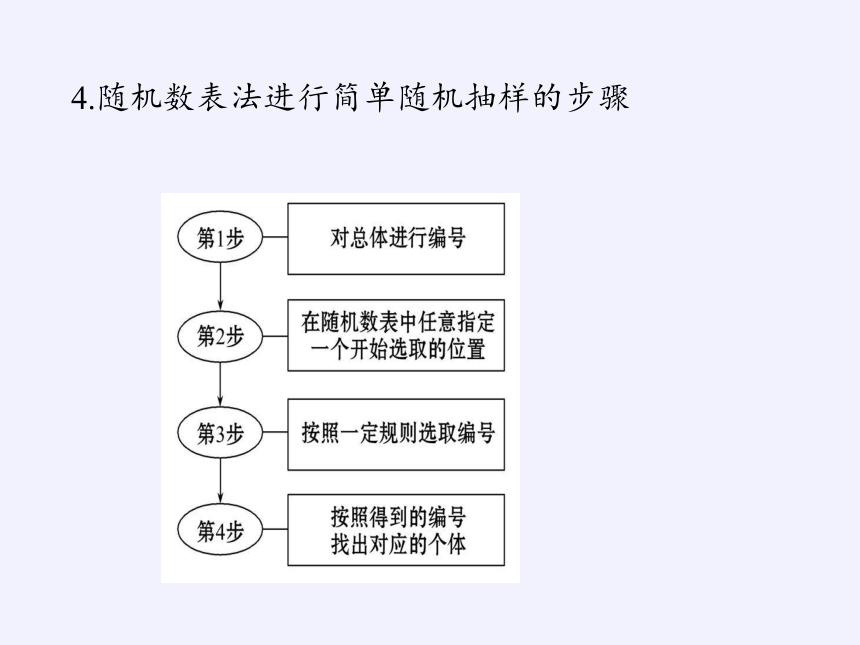
4.随机数表法进行简单随机抽样的步骤
【思考】
用随机数表进行简单随机抽样的规则是什么?
提示:(1)定方向:读数的方向(向左、向右、向上或向下都可以)。
(2)读数规则:读数时结合编号的特点进行读取,编号为两位数则两位两位地读取,编号为三位数则三位三位地读取,若得到的号码不在编号中或已被选用,则跳过,直到选满所需号码为止。
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)要想准确知道全班同学的平均年龄,应进行普查。( )
(2)简单随机抽样也可以是有放回抽样。( )
(3)简单随机抽样中每个个体被抽到的机会相等。( )
(4)当总体容量很大时,不宜采用抽签法。( )
提示:(1)√。抽样调查无法获得准确的平均年龄。
(2)×。简单随机抽样是不放回抽样。
(3)√。简单随机抽样是等可能的抽样。
(4)√。总体容量很大时,抽签法费时费力,且抽取的样本代表性较差。
2.下面问题可以用普查的方式进行调查的是( )
A.检验一批钢材的抗拉强度
B.检验海水中微生物的含量
C.检验10件产品的质量
D.检验一批汽车的使用寿命
【解析】选C。A不能用普查的方式进行调查,因为这种试验具有破坏性;B用普查的方式无法完成;D试验具有破坏性,且需要耗费大量的时间,在实际生产中无法应用。
3.参加运动会的800名运动员的体重情况,从中抽查了80名运动员的体重,就这个问题来说,下列说法正确的是( )
A.800名运动员是总体 B.每个运动员是个体
C.抽取的80名运动员是样本 D.样本容量是80
【解析】选D。此问题研究的是运动员的体重情况,不是运动员,故A,B,C错误。
4.抽签法中确保样本代表性的关键是( )
A.制签 B.搅拌均匀
C.逐一抽取 D.抽取不放回
【解析】选B。只有搅拌均匀才能保证抽样的公平。
5.从10个篮球中任取一个,检查其质量,用随机数表法抽取样本,则编号应为( )
A.1,2,3,4,5,6,7,8,9,10
B.-5,-4,-3,-2,-1,0,1,2,3,4
C.10,20,30,40,50,60,70,80,90,100
D.0,1,2,3,4,5,6,7,8,9
【解析】选D。用随机数表法抽取样本,则编号位数应相同,且不能为负数。
类型一 简单随机抽样的有关概念
【典例】1.若对某校1200名学生的耐力做调查,抽取其中120名学生,测试他们1500米跑的成绩,得出相应的数值,在这项调查中,样本是指( )
A.120名学生
B.1200名学生
C.120名学生1500米跑的成绩
D.1200名学生1500米跑的成绩
2.用简单随机抽样从100名学生(男生25人)中抽选20人进行评教,某男学生被抽到的可能性是________。
3.下面的抽样方法是简单随机抽样吗?为什么?
(1)从无数个个体中抽取50个个体作为样本。
(2)仓库中有1万支奥运火炬,从中一次性抽取100支火炬进行质量检查。
(3)某连队从200名党员官兵中,挑选出50名最优秀的官兵赶赴灾区参加抗震救灾工作。
(4)一彩民选号,从装有33个大小、形状都相同的号签的盒子中无放回地抽出6个号签。
【思维·引】
1.依据样本的定义解答。
2.依据简单随机抽样是等可能地抽取解答,即在整个抽样过程中,每个个体被抽取的可能性相等,均为样本容量与总体容量之比。
3.依据简单随机抽样的定义判断。
【解析】
1.选C。本题抽取的是120名学生1500米跑的成绩,因此每个学生1500米跑的成绩是个体,这120名学生1500米跑的成绩构成样本。
2.因为样本容量为20,总体容量为100,所以总体中每个个体被抽到的可能性都为 =0.2。
答案:0.2
3.(1)不是简单随机抽样.因为简单随机抽样要求被抽取样本的总体的个数是有限的。
(2)不是简单随机抽样。虽然“一次性抽取”和“逐个抽取”不影响个体被抽到的可能性,但简单随机抽样要求的是“逐个抽取”。
(3)不是简单随机抽样。因为这50名官兵是从中挑选出来的,是最优秀的,每个个体被抽到的可能性不同,不符合简单随机抽样中“等可能抽样”的要求。
(4)是简单随机抽样。因为总体中的个体数是有限的,并且是从总体中逐个进行抽取的,是不放回、等可能的抽样。
【内化·悟】
在抽样调查中,确定总体、个体、样本要注意什么?
提示:要注意说明研究的是哪些指标。如本例1中,研究的是学生1500米跑的成绩。
【类题·通】
简单随机抽样必须具备下列特点:
(1)被抽取样本的总体中的个体数N是有限的;
(2)被抽取的样本数n小于或等于样本总体中的个体数N;
(3)抽取的样本是从总体中逐个抽取的;
(4)简单随机抽样是一种不放回抽样;
(5)简单随机抽样是一种等可能的抽样。每次从总体中抽取一个个体时,每个个体被抽取的可能性相等,均为样本容量与总体容量之比。
(4)简单随机抽样是一种不放回抽样;
(5)简单随机抽样是一种等可能的抽样。每次从总体中抽取一个个体时,每个个体被抽取的可能性相等,均为样本容量与总体容量之比。
【习练·破】
下面抽样方法是简单随机抽样的是( )
A.从平面直角坐标系中抽取5个点作为样本
B.某饮料公司从仓库中的10000瓶饮料中一次性抽取50瓶进行质量检查
C.某学校从100名学生中,选出10名数学好的学生去参加数学竞赛
D.从10个笔记本电脑中不放回地随机抽取2个进行质量检验(假设10个笔记本电脑已编好号,对编号随机抽取)
C.某学校从100名学生中,选出10名数学好的学生去参加数学竞赛
D.从10个笔记本电脑中不放回地随机抽取2个进行质量检验(假设10个笔记本电脑已编好号,对编号随机抽取)
【解析】选D。A中平面直角坐标系中有无数个点,这与要求总体中的个体数有限不相符,故错误;B中一次性抽取不符合简单随机抽样逐个抽取的特点,故错误;C中选出10名数学好的学生,不符合简单随机抽样的等可能性,故错误。
【加练·固】
1.为了了解高一年级学生的视力情况,特别是近视率问题,抽测了其中100名同学的视力情况。在这个过程中,100名同学的视力情况(数据)是( )
A.总体 B.个体
C.总体的一个样本 D.样本容量
【解析】选C。100名同学的视力情况(数据)是从总体中抽取的一部分个体所组成的集合,所以是总体的一个样本。
2.一个总体中共有200个个体,用简单随机抽样的方法从中抽取一个容量为20的样本,则某一特定个体被抽到的可能性是________。
【解析】简单随机抽样过程中,每个个体被抽到的可能性相等,所以从200个个体中抽取一个容量为20的样本,每个个体被抽到的可能性都是 。
答案:
类型二 抽签法
【典例】要从某汽车厂生产的30辆汽车中随机抽取3辆进行测试。请选择合适的抽样方法,并写出抽样过程。
【思维·引】已知N=30,n=3。抽签法抽样时编号1,2,…,30,抽取3个编号,对应的汽车组成样本。
【解析】应使用抽签法,步骤如下:
①将30辆汽车编号,号码是1,2,3,…,30;
②将1~30这30个编号分别写到大小、形状都相同的纸片上;
③将写好的纸片放入一个不透明的容器中,并搅拌均匀;
④从容器中每次抽取一个纸片,连续抽取3次,并记录上面的编号;
⑤所得号码对应的3辆汽车就是要抽取的对象。
【内化·悟】
抽签法是如何保证所取样本具有代表性的?
提示:写编号用的纸片或小球,大小、形状、颜色等完全一致,放到容器中,搅拌均匀,随机抽取编号。
【类题·通】
抽签法的5个步骤
【习练·破】
学校举办元旦晚会,需要从每班选10名男生,8名女生参加合唱节目。某班有男生32名,女生28名,试用抽签法确定该班参加合唱的同学。
【解析】第一步,将32名男生从1到32进行编号;
第二步,用大小形状都相同的纸做成32个纸片,在每个纸片上分别写上这些编号;
第三步,将写好的纸片放在一个容器内摇匀,不放回地逐个从中抽出10个纸片;
第四步,相应编号的男生参加合唱;
第五步,用相同的办法从28名女生中选出8名女生参加合唱。
【加练·固】
现要从20名学生中抽取5名进行问卷调查,写出抽取样本的过程。
【解析】①先将20名学生进行编号,从1编到20;
②把号码写在形状、大小均相同的号签上;
③将号签放在某个不透明的箱子中进行充分搅拌,力求均匀,然后依次从箱子中抽取5个号签,按这5个号签上的号码找出对应的学生,即得样本。
类型三 用随机数表进行简单随机抽样
【典例】现从80瓶水中抽取6瓶进行检验,利用随机数表抽取样本时,先将80瓶水编号,可以编为00,01,02,…,79,在随机数表中任选一个数,例如,选出第6行第1组第5个数7(下面摘取了一个随机数表的第6行至第10行)。
16227 79439 49544 35482 17379 32378 87352 09643 84263 49164
84421 75331 57245 50688 77047 44767 21763 35025 83921 20676
63016 37859 16955 56719 98105 07175 12867 35807 44395 23879
33211 23429 78645 60782 52420 74438 15510 01342 99660 27954
57608 63244 09472 79654 49174 60962 90528 47727 08027 34328
规定从选定的数7开始向右读,依次得到的样本为________。
【思维·引】从选定的数7开始向右读,每次读取两位,不在编号范围内或重复的号码舍弃,直到取满6个数为止。
【解析】找到第6行第1组第5个数7开始向右读,
第一个符合条件的是77,
第二个数是94,因为它大于79,舍去。
第三个数是39,第四个数是49,
第五个数是54,第六个数是43。
第七个数是54,重复,舍去。
第八个数是82,因为它大于79,舍去。
第九个数是17。
答案:77,39,49,54,43,17
【素养·探】
在与用随机数表进行简单随机抽样有关的问题中,经常利用核心素养中的数据分析,通过研究用随机数表进行简单随机抽样,培养学生应用数学知识解决实际问题的意识,提高学生处理、分析数据的能力。
将本例的条件改为“90瓶水中抽取8瓶进行检验”,选号的起始点不变,应如何编号?抽样结果又如何?
【解析】先将90瓶水编号,可以编为00,01,02,……,89,从第6行第1组第5个数7开始,依次取77,94(舍),39,49,54,43,54(舍),82,17,37。
【类题·通】
在利用随机数表法抽样的过程中需注意的问题
(1)编号要求位数相同。
(2)第一个数字的抽取是随机的。
(3)读数的方向是任意的,且事先定好的。
【习练·破】
总体由编号为00,01,02,…,48,49的50个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第6行的第9列和第10列数字开始,从左到右依次选取两个数字,则选出的第3个个体的编号为( )
附:第6行至第9行的随机数表
2635 7900 3370 9160 1620 3882 7757 4950
3211 4919 7306 4916 7677 8733 9974 6732
2748 6198 7164 4148 7086 2888 8519 1620
7477 0111 1630 2404 2979 7991 9683 5125
A.3 B.16 C.38 D.20
【解析】选D。按随机数表法,从随机数表第6行的第9列和第10列数字开始从左到右依次选取两个数字,则编号依次为33,16,20,38,49,32,则选出的第3个个体的编号为20。
【加练·固】
福利彩票“双色球”中红色球的号码由编号为01,02,…,33的33个个体组成,小明利用如图的随机数表选取6组数作为6个红色球的编号,选取方法是从下面的随机数表第1行的第7列和第8列数字开始,由左到右依次选取两个数字,则选出来的第4个红色球的编号为( )
71913 86754 13581 83476 35542 59552 42378 63932
34855 52612 59565 68923 49376 39673 12035 84310
A.13 B.32 C.25 D.18
【解析】选B。选取方法是从随机数表第1行的第7列和第8列数字开始由左到右依次选取两个数字,则选出的6个红色球的编号依次为13,18,25,32,26,12。所以选出来的第4个红色球的编号为32。
第2课时
分层抽样
分层抽样
(1)定义
一般地,如果相对于要考察的问题来说,总体可以分成有明显差别的、互不重叠的几部分时,每一部分可称为层,在各层中按层在总体中所占比例进行随机抽样的方法称为分层随机抽样(简称为分层抽样)
【思考】
如何理解“层在总体中所占比例”?
提示:从N个个体中抽取n个个体,若将总体分为A,B,C三层,含有的个体数目分别是x,y,z,在A,B,C三层应抽取的个体数目分别是a,b,c,那么
(2)应用的广泛性
①分层抽样所得到的样本,一般更具有代表性,可以更准确地反映总体的特征,尤其是在层内个体相对同质而层间差异较大时。
②分层抽样在各层中抽样时,还可根据各层的特点灵活地选用不同的随机抽样方法。
③想同时获取总体的信息和各层的内部信息时,常采用分层抽样。
【思考】
简单随机抽样和分层抽样的联系和区别是什么?
提示:
类别 简单随机抽样 分层抽样
各自 特点 从总体中逐个抽取 将总体分成几层,分层进行抽取
相互 联系 在各层抽样时采用简单随机抽样
适用 范围 总体中的个体数较少 总体由存在明显差异的几部分组成
共同点 ①抽样过程中每个个体被抽到的可能性相等 ②每次抽出个体后不再放回,即不放回抽样
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)分层抽样实际上是按比例抽样。( )
(2)分层抽样中每个个体被抽到的可能性不一样。( )
(3)分层抽样中不能用简单随机抽样。( )
提示:(1)√。由分层抽样的定义知此说法正确。
(2)×。分层抽样是等可能抽样。
(3)×。分层抽样在各层抽样时,可以灵活选用不同的抽样方法。
2.下列试验中最适合用分层抽样法抽样的是( )
A.从一箱3000个零件中抽取5个入样
B.从一箱3000个零件中抽取600个入样
C.从一箱30个零件中抽取5个入样
D.从甲、乙两厂生产的300个零件中抽取6个入样
【解析】选D。A总体容量较大,样本容量较小,适合用随机数表法;B总体容量较大,且无明显差异,不适合用分层抽样;C总体容量较小,样本容量较小,适合用抽签法;D总体有明显的层次,适合用分层抽样法。
3.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名。现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6 B.8 C.10 D.12
【解析】选B。设在高二年级的学生中抽取x人,
则有 ,解得x=8。
4.某单位有职工100人,不到35岁的有45人,35岁到49岁的有25人,剩下的为50岁以上(包括50岁)的人,用分层抽样的方法从中抽20人,各年龄段分别抽取的人数为( )
A.7,5,8 B.9,5,6
C.7,5,9 D.8,5,7
【解析】选B。由于样本容量与总体中的个体数之比为 ,故各年龄段抽取的人数依次为45× =9(人),25× =5(人),20-9-5=6(人)。
类型一 分层抽样的基本概念
【典例】1.分层抽样是将相似的个体归入一类(层),然后每类抽取若干个个体构成样本,所以分层抽样为保证每个个体等可能被抽取,必须进行( )
A.每层等可能抽样
B.每层可以不等可能抽样
C.所有层按同一抽样比等可能抽样
D.所有层抽个体数量相同
2.下列问题中,采用怎样的抽样方法较为合理?
(1)从10台电冰箱中抽取3台进行质量检查。
(2)某社区有400个家庭,其中高收入家庭100户,中等收入家庭230户,低收入家庭70户,为了调查该社区购买力的某项指标,要从中抽取一个容量为100的样本。
(3)某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本。
【思维·引】1.依据分层抽样在各层中按层在总体中所占比例进行随机抽样解答。
2.抓住分层抽样的特点,即适用于有差异较大的几个部分组成的总体的抽样,根据这个特点来确定分层抽样的应用范围,再由分层抽样的定义,可以判断出所给的抽样方法是否属于分层抽样。
【解析】1.选C。保证每个个体等可能地被抽取是三种基本抽样方式的共同特征,为了保证这一点,分层抽样时必须在所有层都按同一抽样比等可能抽样。
2.(1)总体的个体数较少,用简单随机抽样中的抽签法。
(2)因购买力与收入有关,总体中的个体差异明显,采用分层抽样法。
(3)为了体现学校各类人员对这一问题的不同的意见,采用分层抽样法。
【内化·悟】
分层抽样中分多少层?如何分层?
提示:要视具体情况而定,总的原则是,层内样本的差异要小,各层之间的样本差异要大,且互不重叠。
【类题·通】
1.分层抽样的判断方法
(1)看总体:看总体中个体是否具有明显差异。
(2)看过程:看各部分的样本是否是按各部分在总体中所占的比例实施抽样。
2.分层抽样的分层标准
(1)以调查所要分析和研究的主要变量或相关的变量作为分层的标准。
(2)以那些有明显分层区分的变量作为分层变量。
【习练·破】
1.下列问题中,最适合用分层抽样方法抽样的是( )
A.某电影院有32排座位,每排有40个座位,座位号是1~40。有一次报告会坐满了听众,报告会结束以后为听取意见,要留下32名听众进行座谈
B.从10台冰箱中抽出3台进行质量检查
C.某乡农田有山地8000亩,丘陵12000亩,平地24000亩,洼地4000亩,现抽取农田480亩估计全乡农田平均产量
D.从50个零件中抽取5个做质量检验
【解析】选C。A的总体容量较大,若对总体分层,层与层之间没有明显区别。B的总体容量较小,用简单随机抽样法比较方便;C总体容量较大,且各类田地的产量差别很大,宜采用分层抽样方法;D与B类似。
2.某学院有四个饲养房,分别养有18,54,24,48只白鼠供试验用。某项试验需抽取24只,你认为最合适的抽样方法为。
(1)在每个饲养房各抽取6只。
(2)把所有白鼠都加上编有不同号码的颈圈,用随机抽样法确定24只。
(3)在四个饲养房分别随手提出3,9,4,8只。
(4)先确定在这四个饲养房应分别抽取3,9,4,8只,再由各饲养房自己加号码颈圈,用简单随机抽样法确定各自抽取的对象。
【解析】(1)中对四个饲养房抽取的白鼠平均分,但由于各饲养房所养数量不一,反而造成了每个个体入选的可能性不相等,是错误的方法。
(2)中保证了每个个体入选的可能性相等,但由于没有注意到处在四个不同环境会产生不同差异,不如采用分层抽样可靠性高,且统一编号、统一选择加大了工作量。
(3)中总体采用了分层抽样,但在每个层次中抽取时有一定的主观性,貌似随机,实则每个个体被抽到的可能性无法保证相等。
答案:(4)
类型二 分层抽样中的计算问题
【典例】1.某校有高级教师26人,中级教师104人,其他教师若干人。为了了解该校教师的工资收入情况,若按分层抽样从该校的所有教师中抽取56人进行调查,已知从其他教师中共抽取了16人,则该校共有教师________人。
2.某网站针对“2020年法定节假日调休安排”提出的A,B,C三种放假方案进行了问卷调查,调查结果如下:
支持A方案 支持B方案 支持C方案
35岁以下的人数 200 400 800
35岁以上(含35岁)的人数 100 100 400
(1)从所有参与调查的人中,用分层抽样的方法抽取n人,已知从支持A方案的人中抽取了6人,求n的值。
(2)从支持B方案的人中,用分层抽样的方法抽取5人,这5人中在35岁以上(含35岁)的人数是多少?35岁以下的人数是多少?
【思维·引】1.根据
列方程求解。
2.(1)根据 列方程求n。
(2)35岁以下(含35岁)的人数× 即可;另外要注意35岁以上(含35岁)的人数与35岁以下的人数和为5。
【解析】1.设该校其他教师有x人,
则
解得x=52,经检验,x=52是原方程的根,故全校教师共有26+104+52=182人。
答案:182
2.(1)由题意得
解得n=40。
(2)35岁以下的人数为 ×400=4人,
35岁以上(含35岁)的人数为5-4=1人。
【素养·探】
在与分层抽样中的计算有关的问题中,经常利用核心素养中的数学运算,通过总体和样本中各层个体数量的比例关系,求出有关量,培养学生计算能力。
将本例的条件改为“A,B,C三种放假方案人数之比为2∶3∶5。现用分层抽样方法抽出一个容量为n的样本,样本中A方案有16人”,求样本的容量n。
【解析】由于A,B,C三种放假方案人数之比为2∶3∶5,样本中A方案有16人,则 ,解得n=80。
【类题·通】
分层抽样中的求解技巧
(1)
(2)总体中某两层的个体数之比=样本中这两层抽取的个体数之比。
【习练·破】
交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查。假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人。若在甲、乙、丙、丁四个
社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为 ( )
A.101 B.808 C.1212 D.2012
【解析】选B。由题意知抽样比为 ,而四个社区一共
抽取的驾驶员人数为12+21+25+43=101,故有 = ,解得N=808。
【加练·固】
某校共有3200名学生,其中高一、高二、高三学生人数的比例为5∶3∶2,从所有学生中抽取一个容量为400的样本,采用哪种抽样方法更合理?高一、高二、高三学生应分别抽取多少?
【解析】由于高一,高二,高三学生人数的比例不同,用分层抽样的方法更合理;
高一学生抽取的人数为400× =200(人)。
高二学生抽取的人数为400× =120(人)。
高三学生抽取的人数为400× =80(人)。
类型三 抽样方法的综合应用
【典例】为了对某课题进行讨论研究,用分层抽样的方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表。(单位:人)
高校 相关人数 抽取人数
A x 1
B 36 y
C 54 3
(1)求x,y。
(2)若从高校B相关的人中选2人进行专题发言,应采用什么抽样方法,请写出合理的抽样过程。
【思维·引】观察特征,确定抽样方法,求出比例,确定各层样本数。
【解析】(1)分层抽样是按各层相关人数和抽取人数的比例进行的,所以有 x=18, y=2,故x=18,y=2。
(2)总体容量和样本容量较小,所以应采用抽签法,过程如下:
第一步 将36人随机分号,号码为1,2,3,…,36;
第二步 将号码分别写在相同的纸片上,揉成团,制成号签;
第三步 将号签放入一个不透明的容器中,充分搅匀,依次抽取2个号码,并记录上面的号码。
第四步 把与号码相对应的人抽出,即可得到所要的样本。
【类题·通】
抽样方法的综合应用
(1)抽样方法的选取原则
若总体由差异明显的几个层次组成,则选用分层抽样。若总体没有差异明显的层次,则考虑采用简单随机抽样。当总体容量较小时宜用抽签法;当总体容量较大,样本容量较小时宜用随机数表法。
(2)抽样方法的应用原则
分层抽样实质是利用已知信息尽量使样本结构与总体结构相似。在实际操作时,并不排斥与其他抽样方法联合使用。
【习练·破】
(2019·驻马店高一检测)某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍,为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为( )
A.9 B.18 C.27 D.36
【解析】选B。设老年职工有x人,中年职工人数是老年职工人数的2倍,则中年职工有2x人,
因为x+2x+160=430,
所以x=90,
即由比例可得该单位老年职工共有90人,
因为在抽取的样本中有青年职工32人,所以每个个体被抽到的概率是 ,用分层抽样的比例应抽取 ×90=18(人)。
【加练·固】
一个单位有职工500人,其中不到35岁的有125人,35岁至49岁的有280人,50岁及50岁以上的有95人。为了了解这个单位职工与身体状态有关的某项指标,要从中抽取100名职工作为样本,职工年龄与这项指标有关,应该怎样抽取?
【解析】用分层抽样来抽取样本,步骤如下:
(1)分层。按年龄将500名职工分成三层:不到35岁的职工;35岁至49岁的职工;50岁及50岁以上的职工。
(2)确定每层抽取个体的个数.抽样比为 ,则在不到35岁的职工中抽取125× =25(人);在35岁至49岁的职工中抽取280× =56(人);在50岁及50岁以上的职工中抽取95× =19(人)。
(3)在各层分别按随机数表法抽取样本。
(4)汇总每层抽样,组成样本。
谢 谢
数据的收集
第1课时 总体与样本及简单随机抽样
1.统计的相关概念
总体 所考察问题涉及的对象全体是总体
个体 总体中每个对象都是个体。
样本 抽取的部分对象组成总体的一个样本
样本 容量 一个样本中包含的个体数目是样本容量
2.普查与抽样调查
一般地,对总体中每个个体都进行考察的方法称为普查(也称全面调查),只抽取样本进行考察的方法称为抽样调查。
3.简单随机抽样
(1)定义:一般地,简单随机抽样(也称纯随机抽样)就是从总体中不加任何分组、划类、排队等,完全随机地抽取个体。
(2)两种常见方法:①抽签法;②随机数表法。
【思考】
抽签法与随机数表法的异同点是什么?
提示:
抽签法 随机数表法
不同点 ①抽签法比随机数表法简单;②抽签法适用于总体中的个体数相对较少的情况 ①随机数表法要求编号的位数相同;②随机数表法适用于总体中的个体数相对较多的情况
相同点 ①都是简单随机抽样,并且要求被抽取样本的总体的个数有限;②都是从总体中逐个不放回地抽取
4.随机数表法进行简单随机抽样的步骤
【思考】
用随机数表进行简单随机抽样的规则是什么?
提示:(1)定方向:读数的方向(向左、向右、向上或向下都可以)。
(2)读数规则:读数时结合编号的特点进行读取,编号为两位数则两位两位地读取,编号为三位数则三位三位地读取,若得到的号码不在编号中或已被选用,则跳过,直到选满所需号码为止。
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)要想准确知道全班同学的平均年龄,应进行普查。( )
(2)简单随机抽样也可以是有放回抽样。( )
(3)简单随机抽样中每个个体被抽到的机会相等。( )
(4)当总体容量很大时,不宜采用抽签法。( )
提示:(1)√。抽样调查无法获得准确的平均年龄。
(2)×。简单随机抽样是不放回抽样。
(3)√。简单随机抽样是等可能的抽样。
(4)√。总体容量很大时,抽签法费时费力,且抽取的样本代表性较差。
2.下面问题可以用普查的方式进行调查的是( )
A.检验一批钢材的抗拉强度
B.检验海水中微生物的含量
C.检验10件产品的质量
D.检验一批汽车的使用寿命
【解析】选C。A不能用普查的方式进行调查,因为这种试验具有破坏性;B用普查的方式无法完成;D试验具有破坏性,且需要耗费大量的时间,在实际生产中无法应用。
3.参加运动会的800名运动员的体重情况,从中抽查了80名运动员的体重,就这个问题来说,下列说法正确的是( )
A.800名运动员是总体 B.每个运动员是个体
C.抽取的80名运动员是样本 D.样本容量是80
【解析】选D。此问题研究的是运动员的体重情况,不是运动员,故A,B,C错误。
4.抽签法中确保样本代表性的关键是( )
A.制签 B.搅拌均匀
C.逐一抽取 D.抽取不放回
【解析】选B。只有搅拌均匀才能保证抽样的公平。
5.从10个篮球中任取一个,检查其质量,用随机数表法抽取样本,则编号应为( )
A.1,2,3,4,5,6,7,8,9,10
B.-5,-4,-3,-2,-1,0,1,2,3,4
C.10,20,30,40,50,60,70,80,90,100
D.0,1,2,3,4,5,6,7,8,9
【解析】选D。用随机数表法抽取样本,则编号位数应相同,且不能为负数。
类型一 简单随机抽样的有关概念
【典例】1.若对某校1200名学生的耐力做调查,抽取其中120名学生,测试他们1500米跑的成绩,得出相应的数值,在这项调查中,样本是指( )
A.120名学生
B.1200名学生
C.120名学生1500米跑的成绩
D.1200名学生1500米跑的成绩
2.用简单随机抽样从100名学生(男生25人)中抽选20人进行评教,某男学生被抽到的可能性是________。
3.下面的抽样方法是简单随机抽样吗?为什么?
(1)从无数个个体中抽取50个个体作为样本。
(2)仓库中有1万支奥运火炬,从中一次性抽取100支火炬进行质量检查。
(3)某连队从200名党员官兵中,挑选出50名最优秀的官兵赶赴灾区参加抗震救灾工作。
(4)一彩民选号,从装有33个大小、形状都相同的号签的盒子中无放回地抽出6个号签。
【思维·引】
1.依据样本的定义解答。
2.依据简单随机抽样是等可能地抽取解答,即在整个抽样过程中,每个个体被抽取的可能性相等,均为样本容量与总体容量之比。
3.依据简单随机抽样的定义判断。
【解析】
1.选C。本题抽取的是120名学生1500米跑的成绩,因此每个学生1500米跑的成绩是个体,这120名学生1500米跑的成绩构成样本。
2.因为样本容量为20,总体容量为100,所以总体中每个个体被抽到的可能性都为 =0.2。
答案:0.2
3.(1)不是简单随机抽样.因为简单随机抽样要求被抽取样本的总体的个数是有限的。
(2)不是简单随机抽样。虽然“一次性抽取”和“逐个抽取”不影响个体被抽到的可能性,但简单随机抽样要求的是“逐个抽取”。
(3)不是简单随机抽样。因为这50名官兵是从中挑选出来的,是最优秀的,每个个体被抽到的可能性不同,不符合简单随机抽样中“等可能抽样”的要求。
(4)是简单随机抽样。因为总体中的个体数是有限的,并且是从总体中逐个进行抽取的,是不放回、等可能的抽样。
【内化·悟】
在抽样调查中,确定总体、个体、样本要注意什么?
提示:要注意说明研究的是哪些指标。如本例1中,研究的是学生1500米跑的成绩。
【类题·通】
简单随机抽样必须具备下列特点:
(1)被抽取样本的总体中的个体数N是有限的;
(2)被抽取的样本数n小于或等于样本总体中的个体数N;
(3)抽取的样本是从总体中逐个抽取的;
(4)简单随机抽样是一种不放回抽样;
(5)简单随机抽样是一种等可能的抽样。每次从总体中抽取一个个体时,每个个体被抽取的可能性相等,均为样本容量与总体容量之比。
(4)简单随机抽样是一种不放回抽样;
(5)简单随机抽样是一种等可能的抽样。每次从总体中抽取一个个体时,每个个体被抽取的可能性相等,均为样本容量与总体容量之比。
【习练·破】
下面抽样方法是简单随机抽样的是( )
A.从平面直角坐标系中抽取5个点作为样本
B.某饮料公司从仓库中的10000瓶饮料中一次性抽取50瓶进行质量检查
C.某学校从100名学生中,选出10名数学好的学生去参加数学竞赛
D.从10个笔记本电脑中不放回地随机抽取2个进行质量检验(假设10个笔记本电脑已编好号,对编号随机抽取)
C.某学校从100名学生中,选出10名数学好的学生去参加数学竞赛
D.从10个笔记本电脑中不放回地随机抽取2个进行质量检验(假设10个笔记本电脑已编好号,对编号随机抽取)
【解析】选D。A中平面直角坐标系中有无数个点,这与要求总体中的个体数有限不相符,故错误;B中一次性抽取不符合简单随机抽样逐个抽取的特点,故错误;C中选出10名数学好的学生,不符合简单随机抽样的等可能性,故错误。
【加练·固】
1.为了了解高一年级学生的视力情况,特别是近视率问题,抽测了其中100名同学的视力情况。在这个过程中,100名同学的视力情况(数据)是( )
A.总体 B.个体
C.总体的一个样本 D.样本容量
【解析】选C。100名同学的视力情况(数据)是从总体中抽取的一部分个体所组成的集合,所以是总体的一个样本。
2.一个总体中共有200个个体,用简单随机抽样的方法从中抽取一个容量为20的样本,则某一特定个体被抽到的可能性是________。
【解析】简单随机抽样过程中,每个个体被抽到的可能性相等,所以从200个个体中抽取一个容量为20的样本,每个个体被抽到的可能性都是 。
答案:
类型二 抽签法
【典例】要从某汽车厂生产的30辆汽车中随机抽取3辆进行测试。请选择合适的抽样方法,并写出抽样过程。
【思维·引】已知N=30,n=3。抽签法抽样时编号1,2,…,30,抽取3个编号,对应的汽车组成样本。
【解析】应使用抽签法,步骤如下:
①将30辆汽车编号,号码是1,2,3,…,30;
②将1~30这30个编号分别写到大小、形状都相同的纸片上;
③将写好的纸片放入一个不透明的容器中,并搅拌均匀;
④从容器中每次抽取一个纸片,连续抽取3次,并记录上面的编号;
⑤所得号码对应的3辆汽车就是要抽取的对象。
【内化·悟】
抽签法是如何保证所取样本具有代表性的?
提示:写编号用的纸片或小球,大小、形状、颜色等完全一致,放到容器中,搅拌均匀,随机抽取编号。
【类题·通】
抽签法的5个步骤
【习练·破】
学校举办元旦晚会,需要从每班选10名男生,8名女生参加合唱节目。某班有男生32名,女生28名,试用抽签法确定该班参加合唱的同学。
【解析】第一步,将32名男生从1到32进行编号;
第二步,用大小形状都相同的纸做成32个纸片,在每个纸片上分别写上这些编号;
第三步,将写好的纸片放在一个容器内摇匀,不放回地逐个从中抽出10个纸片;
第四步,相应编号的男生参加合唱;
第五步,用相同的办法从28名女生中选出8名女生参加合唱。
【加练·固】
现要从20名学生中抽取5名进行问卷调查,写出抽取样本的过程。
【解析】①先将20名学生进行编号,从1编到20;
②把号码写在形状、大小均相同的号签上;
③将号签放在某个不透明的箱子中进行充分搅拌,力求均匀,然后依次从箱子中抽取5个号签,按这5个号签上的号码找出对应的学生,即得样本。
类型三 用随机数表进行简单随机抽样
【典例】现从80瓶水中抽取6瓶进行检验,利用随机数表抽取样本时,先将80瓶水编号,可以编为00,01,02,…,79,在随机数表中任选一个数,例如,选出第6行第1组第5个数7(下面摘取了一个随机数表的第6行至第10行)。
16227 79439 49544 35482 17379 32378 87352 09643 84263 49164
84421 75331 57245 50688 77047 44767 21763 35025 83921 20676
63016 37859 16955 56719 98105 07175 12867 35807 44395 23879
33211 23429 78645 60782 52420 74438 15510 01342 99660 27954
57608 63244 09472 79654 49174 60962 90528 47727 08027 34328
规定从选定的数7开始向右读,依次得到的样本为________。
【思维·引】从选定的数7开始向右读,每次读取两位,不在编号范围内或重复的号码舍弃,直到取满6个数为止。
【解析】找到第6行第1组第5个数7开始向右读,
第一个符合条件的是77,
第二个数是94,因为它大于79,舍去。
第三个数是39,第四个数是49,
第五个数是54,第六个数是43。
第七个数是54,重复,舍去。
第八个数是82,因为它大于79,舍去。
第九个数是17。
答案:77,39,49,54,43,17
【素养·探】
在与用随机数表进行简单随机抽样有关的问题中,经常利用核心素养中的数据分析,通过研究用随机数表进行简单随机抽样,培养学生应用数学知识解决实际问题的意识,提高学生处理、分析数据的能力。
将本例的条件改为“90瓶水中抽取8瓶进行检验”,选号的起始点不变,应如何编号?抽样结果又如何?
【解析】先将90瓶水编号,可以编为00,01,02,……,89,从第6行第1组第5个数7开始,依次取77,94(舍),39,49,54,43,54(舍),82,17,37。
【类题·通】
在利用随机数表法抽样的过程中需注意的问题
(1)编号要求位数相同。
(2)第一个数字的抽取是随机的。
(3)读数的方向是任意的,且事先定好的。
【习练·破】
总体由编号为00,01,02,…,48,49的50个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第6行的第9列和第10列数字开始,从左到右依次选取两个数字,则选出的第3个个体的编号为( )
附:第6行至第9行的随机数表
2635 7900 3370 9160 1620 3882 7757 4950
3211 4919 7306 4916 7677 8733 9974 6732
2748 6198 7164 4148 7086 2888 8519 1620
7477 0111 1630 2404 2979 7991 9683 5125
A.3 B.16 C.38 D.20
【解析】选D。按随机数表法,从随机数表第6行的第9列和第10列数字开始从左到右依次选取两个数字,则编号依次为33,16,20,38,49,32,则选出的第3个个体的编号为20。
【加练·固】
福利彩票“双色球”中红色球的号码由编号为01,02,…,33的33个个体组成,小明利用如图的随机数表选取6组数作为6个红色球的编号,选取方法是从下面的随机数表第1行的第7列和第8列数字开始,由左到右依次选取两个数字,则选出来的第4个红色球的编号为( )
71913 86754 13581 83476 35542 59552 42378 63932
34855 52612 59565 68923 49376 39673 12035 84310
A.13 B.32 C.25 D.18
【解析】选B。选取方法是从随机数表第1行的第7列和第8列数字开始由左到右依次选取两个数字,则选出的6个红色球的编号依次为13,18,25,32,26,12。所以选出来的第4个红色球的编号为32。
第2课时
分层抽样
分层抽样
(1)定义
一般地,如果相对于要考察的问题来说,总体可以分成有明显差别的、互不重叠的几部分时,每一部分可称为层,在各层中按层在总体中所占比例进行随机抽样的方法称为分层随机抽样(简称为分层抽样)
【思考】
如何理解“层在总体中所占比例”?
提示:从N个个体中抽取n个个体,若将总体分为A,B,C三层,含有的个体数目分别是x,y,z,在A,B,C三层应抽取的个体数目分别是a,b,c,那么
(2)应用的广泛性
①分层抽样所得到的样本,一般更具有代表性,可以更准确地反映总体的特征,尤其是在层内个体相对同质而层间差异较大时。
②分层抽样在各层中抽样时,还可根据各层的特点灵活地选用不同的随机抽样方法。
③想同时获取总体的信息和各层的内部信息时,常采用分层抽样。
【思考】
简单随机抽样和分层抽样的联系和区别是什么?
提示:
类别 简单随机抽样 分层抽样
各自 特点 从总体中逐个抽取 将总体分成几层,分层进行抽取
相互 联系 在各层抽样时采用简单随机抽样
适用 范围 总体中的个体数较少 总体由存在明显差异的几部分组成
共同点 ①抽样过程中每个个体被抽到的可能性相等 ②每次抽出个体后不再放回,即不放回抽样
【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)分层抽样实际上是按比例抽样。( )
(2)分层抽样中每个个体被抽到的可能性不一样。( )
(3)分层抽样中不能用简单随机抽样。( )
提示:(1)√。由分层抽样的定义知此说法正确。
(2)×。分层抽样是等可能抽样。
(3)×。分层抽样在各层抽样时,可以灵活选用不同的抽样方法。
2.下列试验中最适合用分层抽样法抽样的是( )
A.从一箱3000个零件中抽取5个入样
B.从一箱3000个零件中抽取600个入样
C.从一箱30个零件中抽取5个入样
D.从甲、乙两厂生产的300个零件中抽取6个入样
【解析】选D。A总体容量较大,样本容量较小,适合用随机数表法;B总体容量较大,且无明显差异,不适合用分层抽样;C总体容量较小,样本容量较小,适合用抽签法;D总体有明显的层次,适合用分层抽样法。
3.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名。现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
A.6 B.8 C.10 D.12
【解析】选B。设在高二年级的学生中抽取x人,
则有 ,解得x=8。
4.某单位有职工100人,不到35岁的有45人,35岁到49岁的有25人,剩下的为50岁以上(包括50岁)的人,用分层抽样的方法从中抽20人,各年龄段分别抽取的人数为( )
A.7,5,8 B.9,5,6
C.7,5,9 D.8,5,7
【解析】选B。由于样本容量与总体中的个体数之比为 ,故各年龄段抽取的人数依次为45× =9(人),25× =5(人),20-9-5=6(人)。
类型一 分层抽样的基本概念
【典例】1.分层抽样是将相似的个体归入一类(层),然后每类抽取若干个个体构成样本,所以分层抽样为保证每个个体等可能被抽取,必须进行( )
A.每层等可能抽样
B.每层可以不等可能抽样
C.所有层按同一抽样比等可能抽样
D.所有层抽个体数量相同
2.下列问题中,采用怎样的抽样方法较为合理?
(1)从10台电冰箱中抽取3台进行质量检查。
(2)某社区有400个家庭,其中高收入家庭100户,中等收入家庭230户,低收入家庭70户,为了调查该社区购买力的某项指标,要从中抽取一个容量为100的样本。
(3)某学校有160名教职工,其中教师120名,行政人员16名,后勤人员24名,为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本。
【思维·引】1.依据分层抽样在各层中按层在总体中所占比例进行随机抽样解答。
2.抓住分层抽样的特点,即适用于有差异较大的几个部分组成的总体的抽样,根据这个特点来确定分层抽样的应用范围,再由分层抽样的定义,可以判断出所给的抽样方法是否属于分层抽样。
【解析】1.选C。保证每个个体等可能地被抽取是三种基本抽样方式的共同特征,为了保证这一点,分层抽样时必须在所有层都按同一抽样比等可能抽样。
2.(1)总体的个体数较少,用简单随机抽样中的抽签法。
(2)因购买力与收入有关,总体中的个体差异明显,采用分层抽样法。
(3)为了体现学校各类人员对这一问题的不同的意见,采用分层抽样法。
【内化·悟】
分层抽样中分多少层?如何分层?
提示:要视具体情况而定,总的原则是,层内样本的差异要小,各层之间的样本差异要大,且互不重叠。
【类题·通】
1.分层抽样的判断方法
(1)看总体:看总体中个体是否具有明显差异。
(2)看过程:看各部分的样本是否是按各部分在总体中所占的比例实施抽样。
2.分层抽样的分层标准
(1)以调查所要分析和研究的主要变量或相关的变量作为分层的标准。
(2)以那些有明显分层区分的变量作为分层变量。
【习练·破】
1.下列问题中,最适合用分层抽样方法抽样的是( )
A.某电影院有32排座位,每排有40个座位,座位号是1~40。有一次报告会坐满了听众,报告会结束以后为听取意见,要留下32名听众进行座谈
B.从10台冰箱中抽出3台进行质量检查
C.某乡农田有山地8000亩,丘陵12000亩,平地24000亩,洼地4000亩,现抽取农田480亩估计全乡农田平均产量
D.从50个零件中抽取5个做质量检验
【解析】选C。A的总体容量较大,若对总体分层,层与层之间没有明显区别。B的总体容量较小,用简单随机抽样法比较方便;C总体容量较大,且各类田地的产量差别很大,宜采用分层抽样方法;D与B类似。
2.某学院有四个饲养房,分别养有18,54,24,48只白鼠供试验用。某项试验需抽取24只,你认为最合适的抽样方法为。
(1)在每个饲养房各抽取6只。
(2)把所有白鼠都加上编有不同号码的颈圈,用随机抽样法确定24只。
(3)在四个饲养房分别随手提出3,9,4,8只。
(4)先确定在这四个饲养房应分别抽取3,9,4,8只,再由各饲养房自己加号码颈圈,用简单随机抽样法确定各自抽取的对象。
【解析】(1)中对四个饲养房抽取的白鼠平均分,但由于各饲养房所养数量不一,反而造成了每个个体入选的可能性不相等,是错误的方法。
(2)中保证了每个个体入选的可能性相等,但由于没有注意到处在四个不同环境会产生不同差异,不如采用分层抽样可靠性高,且统一编号、统一选择加大了工作量。
(3)中总体采用了分层抽样,但在每个层次中抽取时有一定的主观性,貌似随机,实则每个个体被抽到的可能性无法保证相等。
答案:(4)
类型二 分层抽样中的计算问题
【典例】1.某校有高级教师26人,中级教师104人,其他教师若干人。为了了解该校教师的工资收入情况,若按分层抽样从该校的所有教师中抽取56人进行调查,已知从其他教师中共抽取了16人,则该校共有教师________人。
2.某网站针对“2020年法定节假日调休安排”提出的A,B,C三种放假方案进行了问卷调查,调查结果如下:
支持A方案 支持B方案 支持C方案
35岁以下的人数 200 400 800
35岁以上(含35岁)的人数 100 100 400
(1)从所有参与调查的人中,用分层抽样的方法抽取n人,已知从支持A方案的人中抽取了6人,求n的值。
(2)从支持B方案的人中,用分层抽样的方法抽取5人,这5人中在35岁以上(含35岁)的人数是多少?35岁以下的人数是多少?
【思维·引】1.根据
列方程求解。
2.(1)根据 列方程求n。
(2)35岁以下(含35岁)的人数× 即可;另外要注意35岁以上(含35岁)的人数与35岁以下的人数和为5。
【解析】1.设该校其他教师有x人,
则
解得x=52,经检验,x=52是原方程的根,故全校教师共有26+104+52=182人。
答案:182
2.(1)由题意得
解得n=40。
(2)35岁以下的人数为 ×400=4人,
35岁以上(含35岁)的人数为5-4=1人。
【素养·探】
在与分层抽样中的计算有关的问题中,经常利用核心素养中的数学运算,通过总体和样本中各层个体数量的比例关系,求出有关量,培养学生计算能力。
将本例的条件改为“A,B,C三种放假方案人数之比为2∶3∶5。现用分层抽样方法抽出一个容量为n的样本,样本中A方案有16人”,求样本的容量n。
【解析】由于A,B,C三种放假方案人数之比为2∶3∶5,样本中A方案有16人,则 ,解得n=80。
【类题·通】
分层抽样中的求解技巧
(1)
(2)总体中某两层的个体数之比=样本中这两层抽取的个体数之比。
【习练·破】
交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查。假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人。若在甲、乙、丙、丁四个
社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为 ( )
A.101 B.808 C.1212 D.2012
【解析】选B。由题意知抽样比为 ,而四个社区一共
抽取的驾驶员人数为12+21+25+43=101,故有 = ,解得N=808。
【加练·固】
某校共有3200名学生,其中高一、高二、高三学生人数的比例为5∶3∶2,从所有学生中抽取一个容量为400的样本,采用哪种抽样方法更合理?高一、高二、高三学生应分别抽取多少?
【解析】由于高一,高二,高三学生人数的比例不同,用分层抽样的方法更合理;
高一学生抽取的人数为400× =200(人)。
高二学生抽取的人数为400× =120(人)。
高三学生抽取的人数为400× =80(人)。
类型三 抽样方法的综合应用
【典例】为了对某课题进行讨论研究,用分层抽样的方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见下表。(单位:人)
高校 相关人数 抽取人数
A x 1
B 36 y
C 54 3
(1)求x,y。
(2)若从高校B相关的人中选2人进行专题发言,应采用什么抽样方法,请写出合理的抽样过程。
【思维·引】观察特征,确定抽样方法,求出比例,确定各层样本数。
【解析】(1)分层抽样是按各层相关人数和抽取人数的比例进行的,所以有 x=18, y=2,故x=18,y=2。
(2)总体容量和样本容量较小,所以应采用抽签法,过程如下:
第一步 将36人随机分号,号码为1,2,3,…,36;
第二步 将号码分别写在相同的纸片上,揉成团,制成号签;
第三步 将号签放入一个不透明的容器中,充分搅匀,依次抽取2个号码,并记录上面的号码。
第四步 把与号码相对应的人抽出,即可得到所要的样本。
【类题·通】
抽样方法的综合应用
(1)抽样方法的选取原则
若总体由差异明显的几个层次组成,则选用分层抽样。若总体没有差异明显的层次,则考虑采用简单随机抽样。当总体容量较小时宜用抽签法;当总体容量较大,样本容量较小时宜用随机数表法。
(2)抽样方法的应用原则
分层抽样实质是利用已知信息尽量使样本结构与总体结构相似。在实际操作时,并不排斥与其他抽样方法联合使用。
【习练·破】
(2019·驻马店高一检测)某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍,为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为( )
A.9 B.18 C.27 D.36
【解析】选B。设老年职工有x人,中年职工人数是老年职工人数的2倍,则中年职工有2x人,
因为x+2x+160=430,
所以x=90,
即由比例可得该单位老年职工共有90人,
因为在抽取的样本中有青年职工32人,所以每个个体被抽到的概率是 ,用分层抽样的比例应抽取 ×90=18(人)。
【加练·固】
一个单位有职工500人,其中不到35岁的有125人,35岁至49岁的有280人,50岁及50岁以上的有95人。为了了解这个单位职工与身体状态有关的某项指标,要从中抽取100名职工作为样本,职工年龄与这项指标有关,应该怎样抽取?
【解析】用分层抽样来抽取样本,步骤如下:
(1)分层。按年龄将500名职工分成三层:不到35岁的职工;35岁至49岁的职工;50岁及50岁以上的职工。
(2)确定每层抽取个体的个数.抽样比为 ,则在不到35岁的职工中抽取125× =25(人);在35岁至49岁的职工中抽取280× =56(人);在50岁及50岁以上的职工中抽取95× =19(人)。
(3)在各层分别按随机数表法抽取样本。
(4)汇总每层抽样,组成样本。
谢 谢
