人教版九年级下册 27.2.1 相似三角形的判定 课件(共23张PPT)
文档属性
| 名称 | 人教版九年级下册 27.2.1 相似三角形的判定 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 536.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 07:29:19 | ||
图片预览




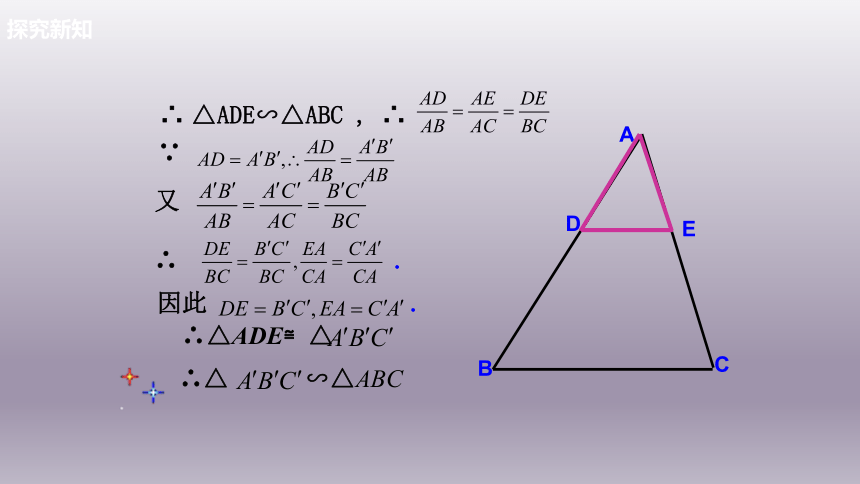

文档简介
(共23张PPT)
27.2.1相似三角形的判定
回顾
1.定义法:两三角形对应角相等,对应边的比相等的两个三角形相似
一、如何判断两三角形是否相似
∵ DE∥BC
∴ △ ADE ∽ △ ABC
D
E
A
B
C
A
B
C
D
E
2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
A型
X型
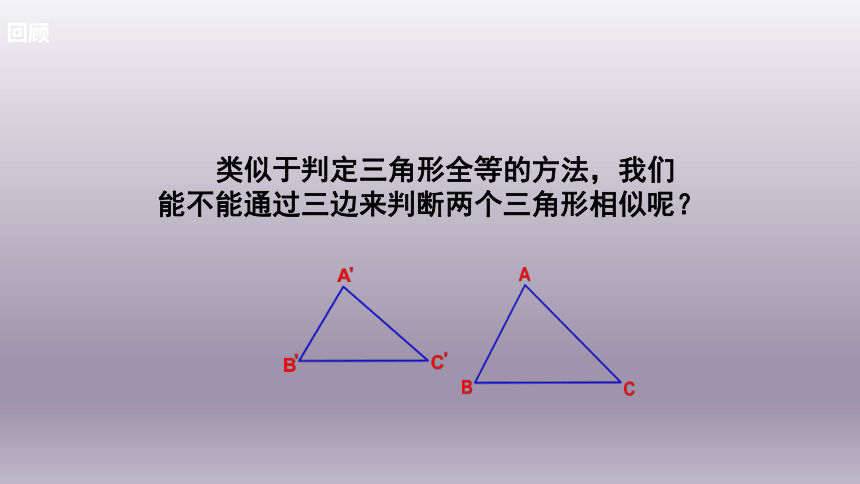
类似于判定三角形全等的方法,我们能不能通过三边来判断两个三角形相似呢?
回顾
是否有△ABC∽△A’B’C’?
A
B
C
C’
B’
A’
三边对应成 比例
回顾
推理论证
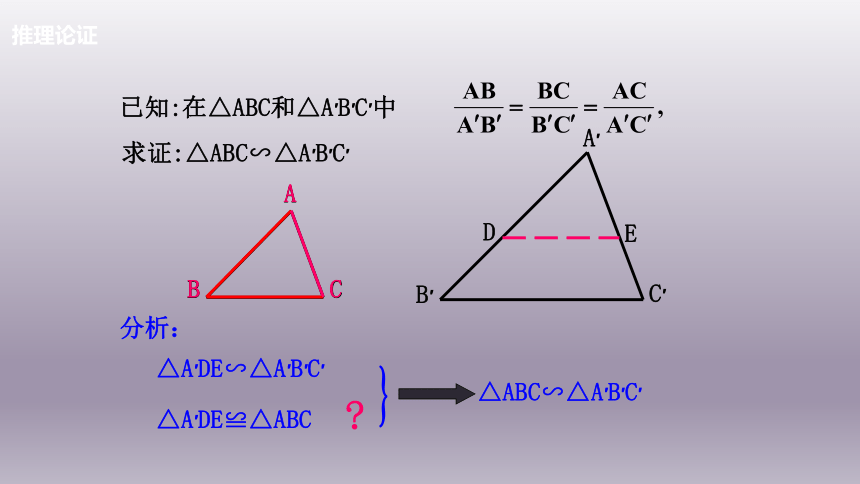
已知:在△ABC和△A′B′C′中
求证:△ABC∽△A′B′C′
B′
A′
C′
B
A
C
E
D
分析:
△A′DE≌△ABC
△A′DE∽△A′B′C′
△ABC∽△A′B′C′
B
A
C
要证明△ABC∽△A’B’C’,可以先作一个与△ABC全等的三角形,证明它△A’B’C’与相似.这里所作的三角形是证明的中介,它把△ABC△A’B’C’联系起来.
推理论证
探究新知
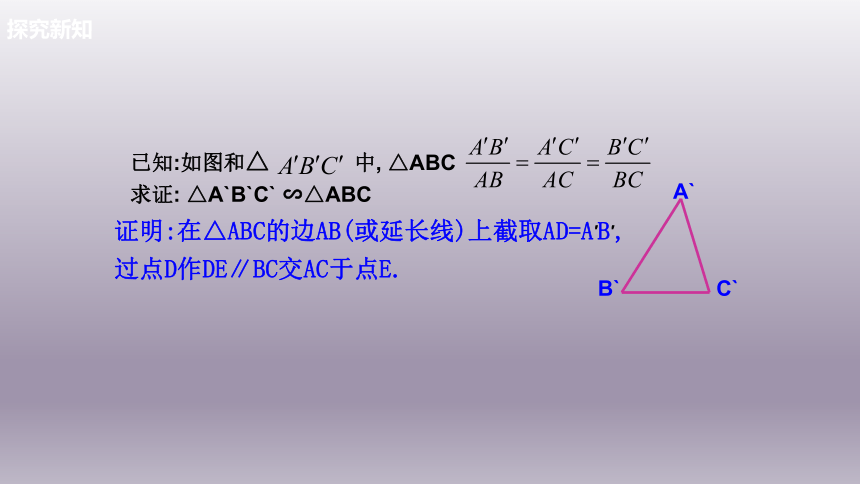
已知:如图和△ 中, △ABC
求证: △A`B`C` ∽△ABC
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A`
B`
C`
过点D作DE∥BC交AC于点E.
A
B
C
D
E
又
∴ △ADE∽△ABC , ∴
∵
∴ .
因此 .
∴△ ∽△ABC
∴△ADE≌△
探究新知
回顾
A
B
C
C’
B’
A’
△ABC∽△A’B’C’
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边对应的比相等,两三角形相似.
例1:
回顾
∴
∵
∴
∽
解:
回顾
例2:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由.
AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=21cm.
回顾
△ABC与△A’B’C‘的三组对应边的比不等,它们不相似.
要使两三角形相似,不改变的AC长,A’C’的长应改为多少?
回顾
练习
1.根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由:
AB=10cm,BC=8cm,AC=16cm,
A’B’=16cm, B’C’=25.6cm A’C’=12.8cm.
2.图中的两个三角形是否相似
练习
运用3
答案是2:1
牛刀小试
1. 根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。
(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12
(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12
(2)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12
△ABC∽△DEF
△ABC∽
不 相 似
△EDF
DE=6,EF=12,DF=8
△ABC∽△DEF
A
B
C
E
D
F
3
4
6
6
8
12
2 如图,判断4×4方格中的两个三角形是否相似,并说明理由.
E
D
F
B
A
C
牛刀小试
运用2
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE
求证:三角形的三条中位线所组成的三角形 与原三角形相似。
已知:
D
A
B
C
E
F
求证:
如图,DE,DF,EF是△ABC的中位线
△ABC∽△FED
证明:
∵ DE,DF,EF是△ABC的中位线
∴ DE= BC,DF= AC,EF= AB
∴
∴ △ABC∽△DEF
运用2
已知:
D
A
B
C
E
F
如图,DE,DF,EF是△ABC的中位线。
(1)请找出图中的相似三角形。
∽
∽
∽
∽
∽
∽
∽
运用2
理解
4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2
要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似
4
5
6
2
谢 谢!
27.2.1相似三角形的判定
回顾
1.定义法:两三角形对应角相等,对应边的比相等的两个三角形相似
一、如何判断两三角形是否相似
∵ DE∥BC
∴ △ ADE ∽ △ ABC
D
E
A
B
C
A
B
C
D
E
2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
A型
X型
类似于判定三角形全等的方法,我们能不能通过三边来判断两个三角形相似呢?
回顾
是否有△ABC∽△A’B’C’?
A
B
C
C’
B’
A’
三边对应成 比例
回顾
推理论证
已知:在△ABC和△A′B′C′中
求证:△ABC∽△A′B′C′
B′
A′
C′
B
A
C
E
D
分析:
△A′DE≌△ABC
△A′DE∽△A′B′C′
△ABC∽△A′B′C′
B
A
C
要证明△ABC∽△A’B’C’,可以先作一个与△ABC全等的三角形,证明它△A’B’C’与相似.这里所作的三角形是证明的中介,它把△ABC△A’B’C’联系起来.
推理论证
探究新知
已知:如图和△ 中, △ABC
求证: △A`B`C` ∽△ABC
证明:在△ABC的边AB(或延长线)上截取AD=A′B′,
A`
B`
C`
过点D作DE∥BC交AC于点E.
A
B
C
D
E
又
∴ △ADE∽△ABC , ∴
∵
∴ .
因此 .
∴△ ∽△ABC
∴△ADE≌△
探究新知
回顾
A
B
C
C’
B’
A’
△ABC∽△A’B’C’
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
简单地说:三边对应的比相等,两三角形相似.
例1:
回顾
∴
∵
∴
∽
解:
回顾
例2:根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由.
AB=4 cm,BC=6cm,AC=8cm,
A’B’=12cm,B’C’=18cm,A’C’=21cm.
回顾
△ABC与△A’B’C‘的三组对应边的比不等,它们不相似.
要使两三角形相似,不改变的AC长,A’C’的长应改为多少?
回顾
练习
1.根据下列条件,判断△ABC与△A’B’C’是否相似,并说明理由:
AB=10cm,BC=8cm,AC=16cm,
A’B’=16cm, B’C’=25.6cm A’C’=12.8cm.
2.图中的两个三角形是否相似
练习
运用3
答案是2:1
牛刀小试
1. 根据下列条件判断△ABC与以D、E、F为顶点的两个三角形是否相似。
(1)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12
(3)AB=3,BC=4,AC=6;
DE=6,EF=9,DF=12
(2)AB=3,BC=4,AC=6;
DE=6,EF=8,DF=12
△ABC∽△DEF
△ABC∽
不 相 似
△EDF
DE=6,EF=12,DF=8
△ABC∽△DEF
A
B
C
E
D
F
3
4
6
6
8
12
2 如图,判断4×4方格中的两个三角形是否相似,并说明理由.
E
D
F
B
A
C
牛刀小试
运用2
试说明∠BAD=∠CAE.
A
D
C
E
B
∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAE
求证:三角形的三条中位线所组成的三角形 与原三角形相似。
已知:
D
A
B
C
E
F
求证:
如图,DE,DF,EF是△ABC的中位线
△ABC∽△FED
证明:
∵ DE,DF,EF是△ABC的中位线
∴ DE= BC,DF= AC,EF= AB
∴
∴ △ABC∽△DEF
运用2
已知:
D
A
B
C
E
F
如图,DE,DF,EF是△ABC的中位线。
(1)请找出图中的相似三角形。
∽
∽
∽
∽
∽
∽
∽
运用2
理解
4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2
要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似
4
5
6
2
谢 谢!
