5.3简单的轴对称图形 第3课时 同步课时作业(含答案)
文档属性
| 名称 | 5.3简单的轴对称图形 第3课时 同步课时作业(含答案) | 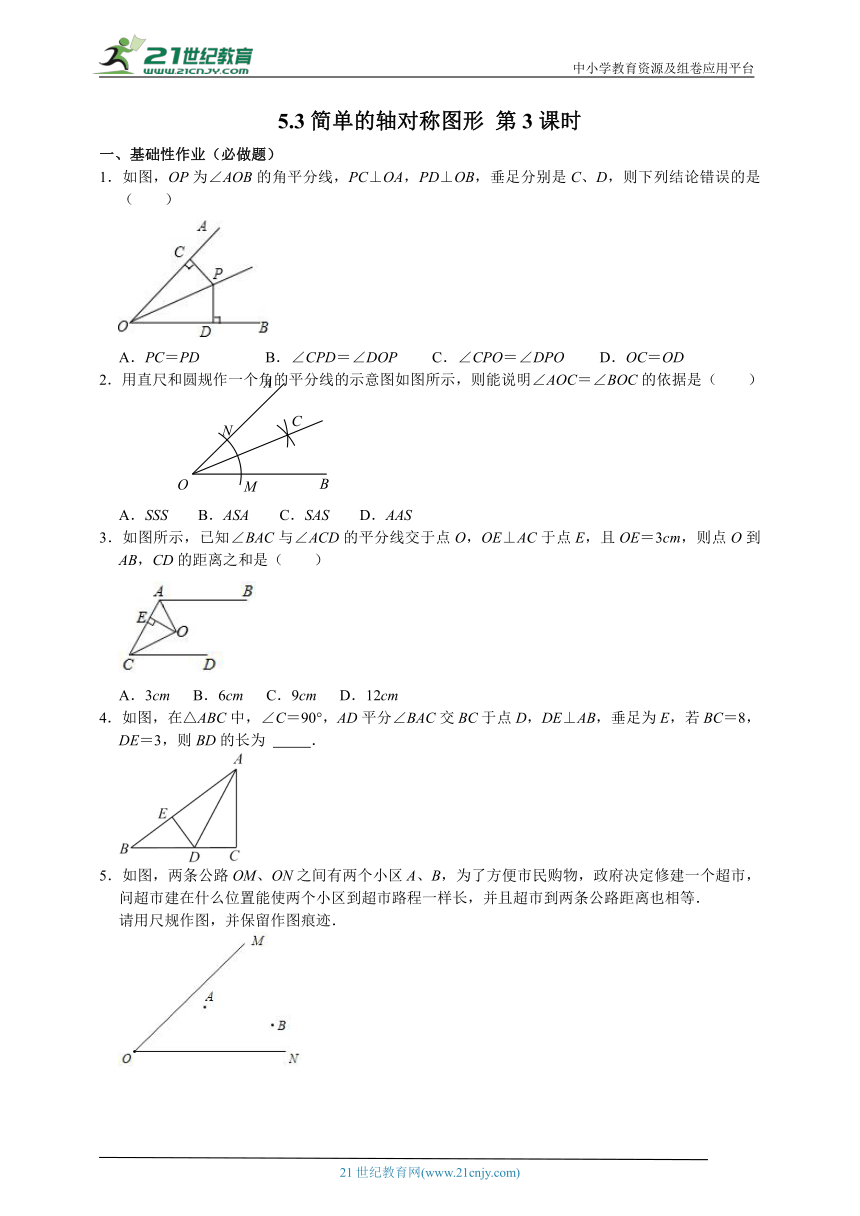 | |
| 格式 | doc | ||
| 文件大小 | 272.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 14:11:28 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
5.3简单的轴对称图形 第3课时
一、基础性作业(必做题)
1.如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
2.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA C.SAS D.AAS
3.如图所示,已知∠BAC与∠ACD的平分线交于点O,OE⊥AC于点E,且OE=3cm,则点O到AB,CD的距离之和是( )
A.3cm B.6cm C.9cm D.12cm
4.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=8,DE=3,则BD的长为 .
5.如图,两条公路OM、ON之间有两个小区A、B,为了方便市民购物,政府决定修建一个超市,问超市建在什么位置能使两个小区到超市路程一样长,并且超市到两条公路距离也相等.
请用尺规作图,并保留作图痕迹.
6.如图,在△ABC中,∠A=36°,∠C=72°,BD是∠ABC的角平分线.
(1)求∠ABD的度数;
(2)若DE⊥AB于点E,AC=6,求AE的长.
拓展性作业(选做题)
1.巩固提升:已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
2.学科拓展:如图1,在△ABC中,若AD是∠BAC的角平分线,过D点分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE=DF.
探究发现:如图2,在△ABC中,仍然有条件“AD是∠BAC的角平分线,点E,F分别在AB和AC上”.若∠AED+∠AFD=180°,则DE与DF是否仍相等?若相等,请证明之;若不相等,请举反例说明.
3.阅读理解:角平分线上的点到角两边的距离相等.这一性质在解决图形面积问题时有何妙用呢?阅读材料:已知,如图(1),在面积为S的△ABC中,BC=a,AC=b,AB=c,三条角平分线的交点O到三边的距离为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB=BC r+AC r+AB r=(a+b+c) r,∴r=
(1)类比推理:若面积为S的四边形ABCD的四条角平分线交于O点,如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求点O到四边的距离r;(用含S、a、b、c、d的代数式表示.)
(2)理解应用:如图(3),在四边形ABCD中,AB∥DC,AB=21,CD=11,AD=BC=13,对角线BD=20,点O1与O2分别为△ABD与△BCD的三条角平分线的交点,设它们到各自三角形三边的距离为r1和r2,求的值.
5.3简单的轴对称图形 第3课时参考答案
一.巩固性作业(必做题)
1.B;2.A;3. B;4.5;
5.如图所示,D点即为所求.
;
6.(1)∵∠A=36°,∠C=72°,
∴∠ABC=180°﹣36°﹣72°=72°,
∵BD是∠ABC的平分线,
∴∠ABD=ABC=36°;
(2)∵∠C=∠ABC=72°,
∴AB=AC=6,
∵∠ABD=∠A=36°,
∴AD=BD,
∵DE⊥AB,
∴AE=BE=AB=3.
二.拓展性作业(选做题)
1. 解:(1)∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积=DF AC=×2×4=4.
2.解:DE=DF.
理由如下:
如图,过点D作DM⊥AB于M,DN⊥AC于N,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN.
∵∠AED+∠AFD=180°,∠AFD+∠DFN=180°,
∴∠DFN=∠AED.
在△DME与△DNF中,
∵,
∴△DME≌△DNF(AAS).
∴DE=DF.
3.(1)如图,连接OA、OB、OC、OD,
∵S=S△AOB+S△BOC+S△COD+S△AOD=ar+br+cr+dr=(a+b+c+d)r,
∴r=;
(2)∵AB∥CD,
∴S△ABD:S△BCD=AB:CD=21:11;
∵r1==,
r2==,
∴=:=×==.
A
C
B
O
M
N
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.3简单的轴对称图形 第3课时
一、基础性作业(必做题)
1.如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
2.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA C.SAS D.AAS
3.如图所示,已知∠BAC与∠ACD的平分线交于点O,OE⊥AC于点E,且OE=3cm,则点O到AB,CD的距离之和是( )
A.3cm B.6cm C.9cm D.12cm
4.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=8,DE=3,则BD的长为 .
5.如图,两条公路OM、ON之间有两个小区A、B,为了方便市民购物,政府决定修建一个超市,问超市建在什么位置能使两个小区到超市路程一样长,并且超市到两条公路距离也相等.
请用尺规作图,并保留作图痕迹.
6.如图,在△ABC中,∠A=36°,∠C=72°,BD是∠ABC的角平分线.
(1)求∠ABD的度数;
(2)若DE⊥AB于点E,AC=6,求AE的长.
拓展性作业(选做题)
1.巩固提升:已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
2.学科拓展:如图1,在△ABC中,若AD是∠BAC的角平分线,过D点分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE=DF.
探究发现:如图2,在△ABC中,仍然有条件“AD是∠BAC的角平分线,点E,F分别在AB和AC上”.若∠AED+∠AFD=180°,则DE与DF是否仍相等?若相等,请证明之;若不相等,请举反例说明.
3.阅读理解:角平分线上的点到角两边的距离相等.这一性质在解决图形面积问题时有何妙用呢?阅读材料:已知,如图(1),在面积为S的△ABC中,BC=a,AC=b,AB=c,三条角平分线的交点O到三边的距离为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB=BC r+AC r+AB r=(a+b+c) r,∴r=
(1)类比推理:若面积为S的四边形ABCD的四条角平分线交于O点,如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求点O到四边的距离r;(用含S、a、b、c、d的代数式表示.)
(2)理解应用:如图(3),在四边形ABCD中,AB∥DC,AB=21,CD=11,AD=BC=13,对角线BD=20,点O1与O2分别为△ABD与△BCD的三条角平分线的交点,设它们到各自三角形三边的距离为r1和r2,求的值.
5.3简单的轴对称图形 第3课时参考答案
一.巩固性作业(必做题)
1.B;2.A;3. B;4.5;
5.如图所示,D点即为所求.
;
6.(1)∵∠A=36°,∠C=72°,
∴∠ABC=180°﹣36°﹣72°=72°,
∵BD是∠ABC的平分线,
∴∠ABD=ABC=36°;
(2)∵∠C=∠ABC=72°,
∴AB=AC=6,
∵∠ABD=∠A=36°,
∴AD=BD,
∵DE⊥AB,
∴AE=BE=AB=3.
二.拓展性作业(选做题)
1. 解:(1)∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积=DF AC=×2×4=4.
2.解:DE=DF.
理由如下:
如图,过点D作DM⊥AB于M,DN⊥AC于N,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN.
∵∠AED+∠AFD=180°,∠AFD+∠DFN=180°,
∴∠DFN=∠AED.
在△DME与△DNF中,
∵,
∴△DME≌△DNF(AAS).
∴DE=DF.
3.(1)如图,连接OA、OB、OC、OD,
∵S=S△AOB+S△BOC+S△COD+S△AOD=ar+br+cr+dr=(a+b+c+d)r,
∴r=;
(2)∵AB∥CD,
∴S△ABD:S△BCD=AB:CD=21:11;
∵r1==,
r2==,
∴=:=×==.
A
C
B
O
M
N
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
