北师大版数学九年级下册 1.1 锐角三角函数 课件(共23张PPT)
文档属性
| 名称 | 北师大版数学九年级下册 1.1 锐角三角函数 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 278.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-09 13:06:54 | ||
图片预览




文档简介
(共23张PPT)
三角函数一般用于计算三角形中未知长度的边和未知的角度在导航、工程学以及物理学方面都有广泛用途。
第一章
直角三角形的边角关系
1 锐角三角函数
教学目标
知识技能
1.经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系
2.能够用tanA表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算。
过程与方法
1.经历观察、猜想等数学活动过程,发展合情推理能力,能有条理地,清晰地阐述自己的观点.
2.体验数形之间的联系,逐步学习利用数形结合的思想分析问题和解决问题.提高解决实际问题的能力.
3.体会解决问题的策略的多样性,发展实践能力和创新精神.
情感态度与价值观
1.积极参与数学活动,对数学产生好奇心和求知欲.
2.形成实事求是的态度以及独立思考的习惯.
教师提问:
1.目前为止我们学过哪些函数,表达式都是什么形式。
2.所学函数的图像、性质。
3.含30度角的直角三角形三边比是多少
交流预习
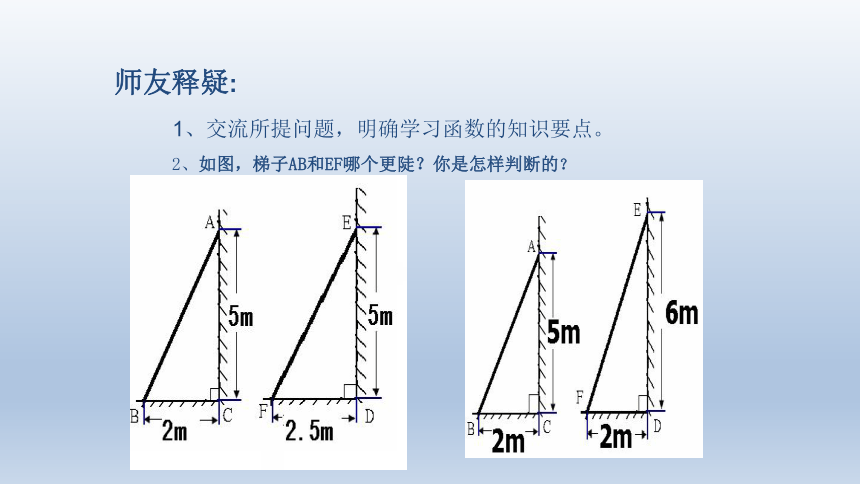
师友释疑:
1、交流所提问题,明确学习函数的知识要点。
2、如图,梯子AB和EF哪个更陡?你是怎样判断的?
3m
3m
2m
4m
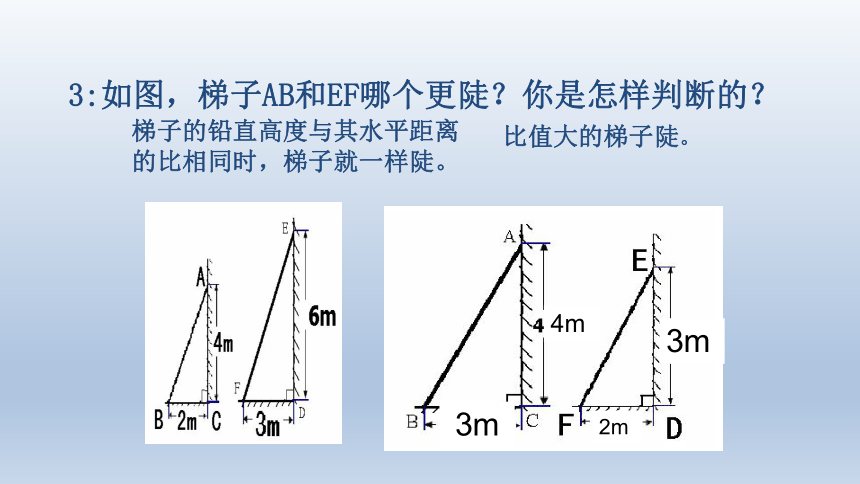
3:如图,梯子AB和EF哪个更陡?你是怎样判断的?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡。
比值大的梯子陡。
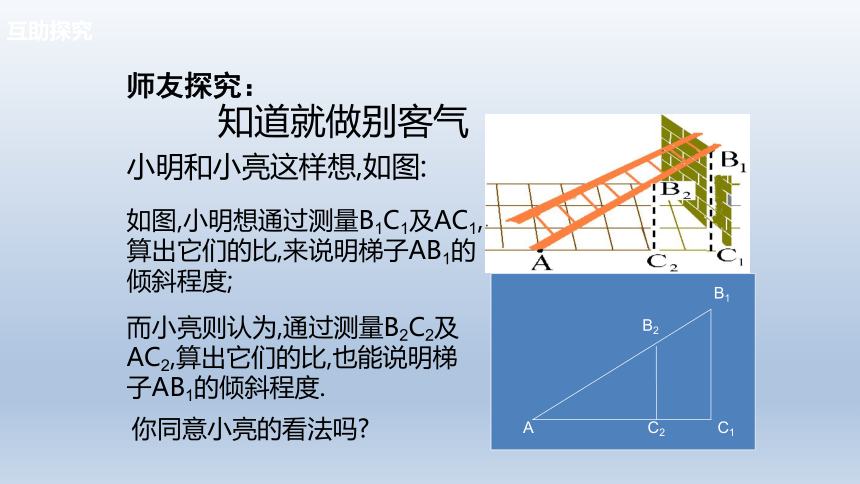
师友探究:
知道就做别客气
小明和小亮这样想,如图:
如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子AB1的倾斜程度;
而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.
你同意小亮的看法吗
A
B1
C2
C1
B2
互助探究
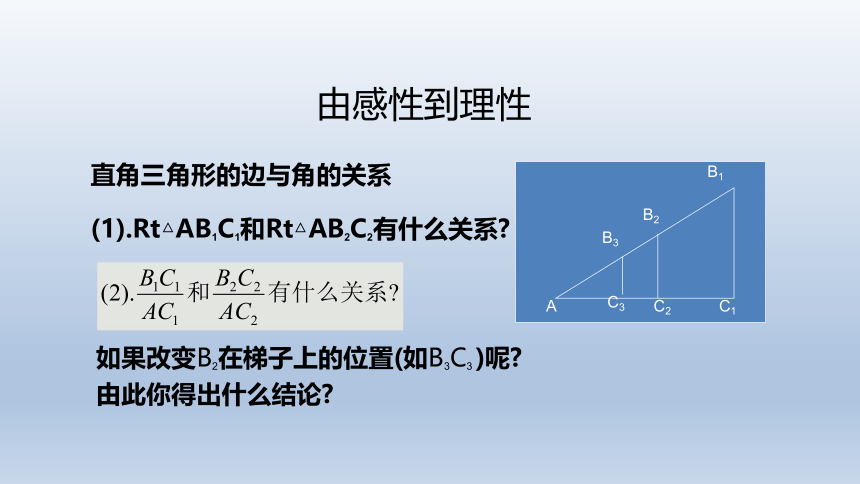
由感性到理性
直角三角形的边与角的关系
(1).Rt△AB1C1和Rt△AB2C2有什么关系
如果改变B2在梯子上的位置(如B3C3 )呢
由此你得出什么结论
A
B1
C2
C1
B2
C3
B3
A
B1
C1
C2
B2
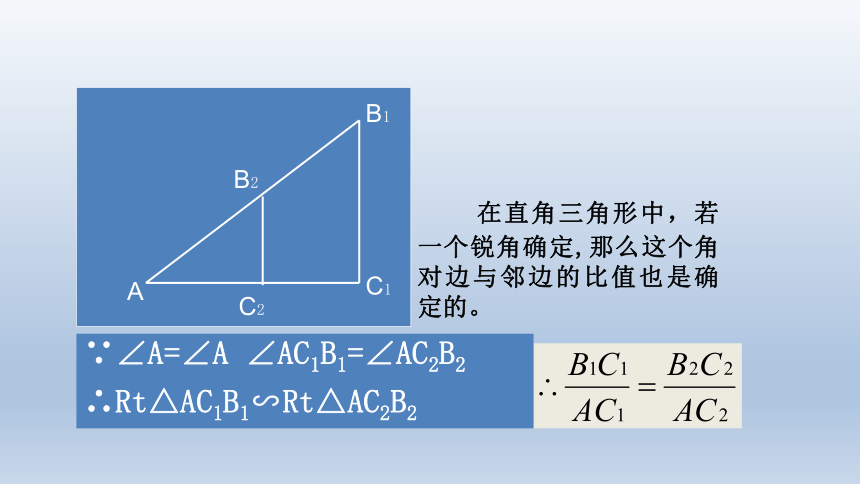
∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2
在直角三角形中,若一个锐角确定,那么这个角对边与邻边的比值也是确定的。
教师讲解:
进步的标志 由感性上升到理性
直角三角形中边与角的关系:锐角的三角函数--正切函数
在直角三角形中,若一个锐角的对边与邻边的比值是一个定值,那么这个角的值也随之确定.
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
如图,梯子AB1的倾斜程度与tanA有关吗 与∠A有关吗
与tanA有关:tanA的值越大,梯子AB1越陡.
与∠A有关:∠A越大,梯子AB1越陡.
A
B1
C2
C1
B2
例1 下图表示两个自动扶梯,那一个自动扶梯比较陡
β
6m
┐
乙
8m
α
5m
┌
甲
13m
解:甲梯中,
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
老师提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
老师提示:
坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切.
100m
60m
┌
α
i
师友训练
1、判断对错:
如图1, (1) tanA= ( )
(2) tanB= ( )
图1
错
错
分层提高
(4) tanB= ( )
如图2:
图2
(3) tanA=0.7m ( )
错
对
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍 C、不变 D、不能确定
C
3.如图,△ABC是等腰三角形,AB=BC,你能根据图中所给数据求出tanC吗?
4
tanC=
4. 在等腰△ABC中,AB=AC=13,BC=10,求tanB。
13
13
10
D
5
12
tanB=12/5
5.如图∠C=90°CD⊥AB,
tanB=
CD
BD
AC
BC
AD
CD
老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.
┌
B
C
A
3
6
(1)
6.在Rt△ABC中,∠C=90°,
(1)如图(1),AC=3,AB=6,求tanA和tanB;
教师提升
师友归纳
1、正切的定义。
2、梯子的倾斜程度与tanA的关系。 (∠A和tanA之间的关系)。
3、数形结合的方法;构造直角三角形的意识。
归纳总结
1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.tanA是一个比值(直角边之比.注意比的顺序,且tanA﹥0,无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等
教师总结
师友检测:
1. 在Rt△ABC中,∠C=90°,AC=5,AB=13,求tanA和tanB.
2.在Rt△ABC中,∠C=90°,BC=3,tanA= ,求AC,AB.
3.观察你们学校,你家或附近的楼梯,看看哪个最陡.
巩固反馈
教师评价:师友互评,总结收获
锐角三角函数函数描述了直角三角形中边与角的关系,它又是一个变量之间重要的函数关系,即新奇,又富有魅力,只不过它的自变量是一个角而不再是实数了。你可要与它建立好感情噢!
三角函数一般用于计算三角形中未知长度的边和未知的角度在导航、工程学以及物理学方面都有广泛用途。
第一章
直角三角形的边角关系
1 锐角三角函数
教学目标
知识技能
1.经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系
2.能够用tanA表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算。
过程与方法
1.经历观察、猜想等数学活动过程,发展合情推理能力,能有条理地,清晰地阐述自己的观点.
2.体验数形之间的联系,逐步学习利用数形结合的思想分析问题和解决问题.提高解决实际问题的能力.
3.体会解决问题的策略的多样性,发展实践能力和创新精神.
情感态度与价值观
1.积极参与数学活动,对数学产生好奇心和求知欲.
2.形成实事求是的态度以及独立思考的习惯.
教师提问:
1.目前为止我们学过哪些函数,表达式都是什么形式。
2.所学函数的图像、性质。
3.含30度角的直角三角形三边比是多少
交流预习
师友释疑:
1、交流所提问题,明确学习函数的知识要点。
2、如图,梯子AB和EF哪个更陡?你是怎样判断的?
3m
3m
2m
4m
3:如图,梯子AB和EF哪个更陡?你是怎样判断的?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡。
比值大的梯子陡。
师友探究:
知道就做别客气
小明和小亮这样想,如图:
如图,小明想通过测量B1C1及AC1,算出它们的比,来说明梯子AB1的倾斜程度;
而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子AB1的倾斜程度.
你同意小亮的看法吗
A
B1
C2
C1
B2
互助探究
由感性到理性
直角三角形的边与角的关系
(1).Rt△AB1C1和Rt△AB2C2有什么关系
如果改变B2在梯子上的位置(如B3C3 )呢
由此你得出什么结论
A
B1
C2
C1
B2
C3
B3
A
B1
C1
C2
B2
∵∠A=∠A ∠AC1B1=∠AC2B2
∴Rt△AC1B1∽Rt△AC2B2
在直角三角形中,若一个锐角确定,那么这个角对边与邻边的比值也是确定的。
教师讲解:
进步的标志 由感性上升到理性
直角三角形中边与角的关系:锐角的三角函数--正切函数
在直角三角形中,若一个锐角的对边与邻边的比值是一个定值,那么这个角的值也随之确定.
A
B
C
∠A的对边
∠A的邻边
┌
tanA=
在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
如图,梯子AB1的倾斜程度与tanA有关吗 与∠A有关吗
与tanA有关:tanA的值越大,梯子AB1越陡.
与∠A有关:∠A越大,梯子AB1越陡.
A
B1
C2
C1
B2
例1 下图表示两个自动扶梯,那一个自动扶梯比较陡
β
6m
┐
乙
8m
α
5m
┌
甲
13m
解:甲梯中,
乙梯中,
∵tanβ>tanα,∴乙梯更陡.
老师提示:在生活中,常用一个锐角的正切表示梯子的倾斜程度.
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
老师提示:
坡面与水平面的夹角(α)称为坡角,坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切.
100m
60m
┌
α
i
师友训练
1、判断对错:
如图1, (1) tanA= ( )
(2) tanB= ( )
图1
错
错
分层提高
(4) tanB= ( )
如图2:
图2
(3) tanA=0.7m ( )
错
对
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍 C、不变 D、不能确定
C
3.如图,△ABC是等腰三角形,AB=BC,你能根据图中所给数据求出tanC吗?
4
tanC=
4. 在等腰△ABC中,AB=AC=13,BC=10,求tanB。
13
13
10
D
5
12
tanB=12/5
5.如图∠C=90°CD⊥AB,
tanB=
CD
BD
AC
BC
AD
CD
老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.
┌
B
C
A
3
6
(1)
6.在Rt△ABC中,∠C=90°,
(1)如图(1),AC=3,AB=6,求tanA和tanB;
教师提升
师友归纳
1、正切的定义。
2、梯子的倾斜程度与tanA的关系。 (∠A和tanA之间的关系)。
3、数形结合的方法;构造直角三角形的意识。
归纳总结
1.tanA是在直角三角形中定义的,∠A是一个锐角(注意数形结合,构造直角三角形).
2.tanA是一个完整的符号,表示∠A的正切,习惯省去“∠”号;
3.tanA是一个比值(直角边之比.注意比的顺序,且tanA﹥0,无单位.
4.tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则正切值相等;两锐角的正切值相等,则这两个锐角相等
教师总结
师友检测:
1. 在Rt△ABC中,∠C=90°,AC=5,AB=13,求tanA和tanB.
2.在Rt△ABC中,∠C=90°,BC=3,tanA= ,求AC,AB.
3.观察你们学校,你家或附近的楼梯,看看哪个最陡.
巩固反馈
教师评价:师友互评,总结收获
锐角三角函数函数描述了直角三角形中边与角的关系,它又是一个变量之间重要的函数关系,即新奇,又富有魅力,只不过它的自变量是一个角而不再是实数了。你可要与它建立好感情噢!
