人教版数学九年级下册 27.3位似-课件(共25张PPT)
文档属性
| 名称 | 人教版数学九年级下册 27.3位似-课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 546.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 10:45:49 | ||
图片预览






文档简介
(共25张PPT)
27.3 位 似
学习目标
1.知道位似图形的概念及性质,理解位似与相似之间的联系与区别;
2.理解并掌握平面坐标系下位似特征;
3.会应用位似解决有关问题.
创设情境 提出问题
问题1: 在日常生活中,我们经常见到这样一类相似的图形,
它们有什么特征?
在日常生活中,经常遇到一些把图形放大或缩小,但不改变图形的形状的情形。经过放大或缩小的图形,与原图形是相似的.用这样的方法,我们可以得到真实的图片和满意的照片.
观察并思考
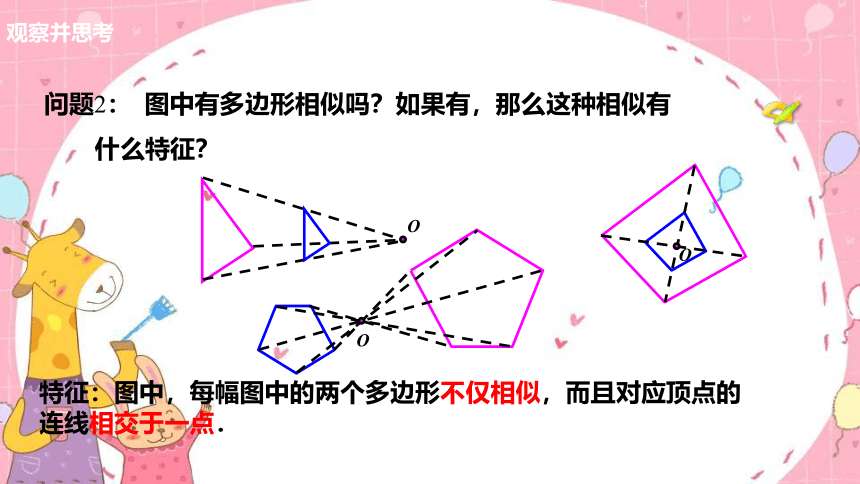
问题2: 图中有多边形相似吗?如果有,那么这种相似有
什么特征?
特征:图中,每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点.
O
O
O
细心辨析 归纳定义
位似图形的概念
如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.这时的相似比又叫位似比.
明确
相似
对应顶点的连线相交于一点
细心辨析 深化理解
位似的特征:
1.位似图形一定是相似形,反之相似形不一定是位似图形.
2.判断位似图形时,要注意首先它们必须是相似形,其次
每一对对应点所在直线都经过同一点.
深化知识 实际应用
利用位似,可以将一个图形放大或缩小.
例如,要把四边形 ABCD 缩小到原来的 .
深化知识 实际应用
O
D
A
B
C
A'
B'
C'
D'
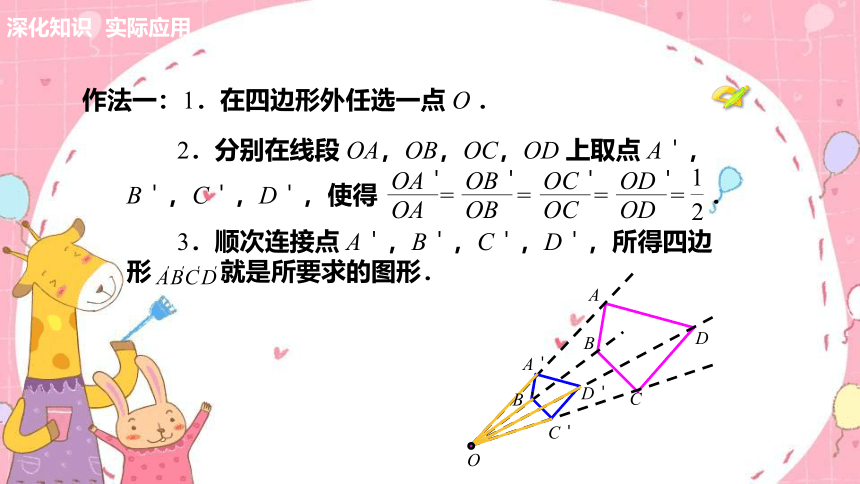
作法一:1.在四边形外任选一点 O .
2.分别在线段 OA,OB,OC,OD 上取点 A',
B',C',D',使得 = = = = .
OA'
OA
OB'
OB
OC'
OC
OD'
OD
3.顺次连接点 A',B',C',D',所得四边形 就是所要求的图形.
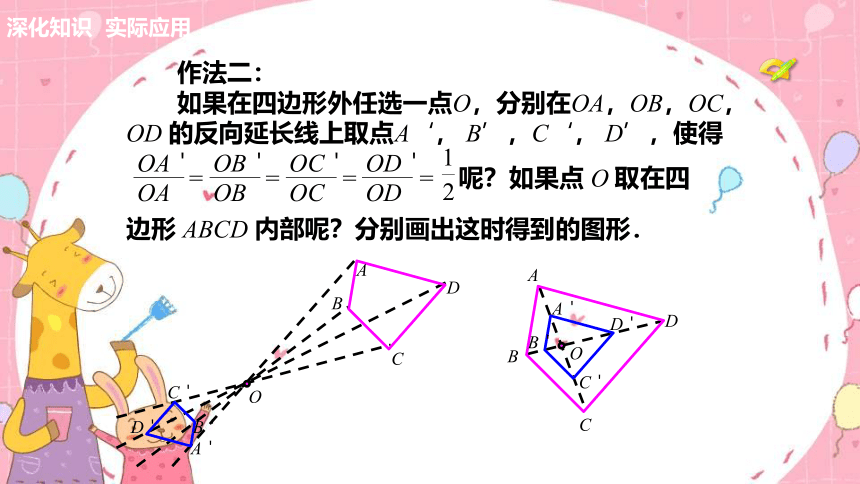
如果在四边形外任选一点O,分别在OA,OB,OC,OD 的反向延长线上取点A‘, B’,C‘, D’,使得
= = = = 呢?如果点 O 取在四
边形 ABCD 内部呢?分别画出这时得到的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
作法二:
OA'
OA
OB'
OB
OC'
OC
OD'
OD
A'
B'
C'
D'
深化知识 实际应用
议一议 练一练
1.如图, △OAB和△OCD是位似图形,AB与CD平行吗 为什么
2.如图,以O为位似中心,将△ABC放大为原来的两倍.
议一议 练一练
3.如图,已知△ABC∽△DEF, 它们对应顶点的连线AD,BE,CF相交于点O,这两个三角形是不是位似三角形
0
B
E
C
F
A
D
议一议 练一练
平移、轴对称、旋转、位似
我们已经学过哪些图形变换?你能说出它们之间的异同吗?
在下列图案中,你能找出哪些变换
观察与发现
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.
A′(2,1),B′(2,0)
观察对应点之间的坐标的变化,你有什么发现
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.
A′(2,1),B′(2,0)
A〞
B〞
A〞(-2,-1),B(-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
观察对应点之间的坐标的变化,你有什么发现
观察与发现
x
y
o
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2.
B
A
C
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
放大后对应点的坐标分别是多少
B'
A'
C'
观察与发现
x
y
o
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
B
A
C
放大后对应点的坐标分别是多少
还有其他办法吗
观察与发现
典例应用 巩固新知
x
y
o
在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),
C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗 试试看.
巩固应用
x
y
o
B
1.如图表示△ABC把它缩小后得到的△COD,求它们的相似比
A
C
D
点D的横坐标为2
点B的横坐标为5
相似比为
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
9
10
11
12
-9
-10
-12
2. 如图,△ABC三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.
A
B
C
解:
A'( , ),B ' ( , ),C ' ( , ),
4
- 4
- 10
8
-4
10
A" ( , ),B" ( , ),C" ( , ),
4
- 4
- 8
10
-10
4
A'
B '
C '
A"
B"
C"
巩固应用
x
y
o
3.如图,写出矩形wxyz各点的坐标,如果矩形STUV相似于wxyz,点S 的坐标为(2,7),按照下列相似比,分别写出T、U、V各点的坐标.
W
x
y
z
(1)相似比为4;
(2)相似比为 ;
巩固应用
巩固应用
典例应用 巩固新知
如图,△ABO 的三个顶点的坐标分别为 A(-2,4),B(-2,0), O(0,0).以原点 O 为位似中心,画出一个三角形,使它与△ABO 的相似比为 .(注意单位长度)
y
x
O
4
4
-4
-4
B
A
归纳小结 自我反思
(1)本节课你学习了哪些知识?
(2)举例说明如何利用位似,将一个图形放大或缩小.
(3)以原点为位似中心的位似图形对应点的坐标有什么关系?用坐标表示位似图形的对应顶点时要注意什么?
(4)本节课运用了哪些数学思想方法研究问题?
布置作业
上本:教科书习题 27.3 第 2,3,4 ,5题.
谢 谢!
27.3 位 似
学习目标
1.知道位似图形的概念及性质,理解位似与相似之间的联系与区别;
2.理解并掌握平面坐标系下位似特征;
3.会应用位似解决有关问题.
创设情境 提出问题
问题1: 在日常生活中,我们经常见到这样一类相似的图形,
它们有什么特征?
在日常生活中,经常遇到一些把图形放大或缩小,但不改变图形的形状的情形。经过放大或缩小的图形,与原图形是相似的.用这样的方法,我们可以得到真实的图片和满意的照片.
观察并思考
问题2: 图中有多边形相似吗?如果有,那么这种相似有
什么特征?
特征:图中,每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点.
O
O
O
细心辨析 归纳定义
位似图形的概念
如果两个图形不仅相似,而且对应顶点的连线相交于一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心.这时的相似比又叫位似比.
明确
相似
对应顶点的连线相交于一点
细心辨析 深化理解
位似的特征:
1.位似图形一定是相似形,反之相似形不一定是位似图形.
2.判断位似图形时,要注意首先它们必须是相似形,其次
每一对对应点所在直线都经过同一点.
深化知识 实际应用
利用位似,可以将一个图形放大或缩小.
例如,要把四边形 ABCD 缩小到原来的 .
深化知识 实际应用
O
D
A
B
C
A'
B'
C'
D'
作法一:1.在四边形外任选一点 O .
2.分别在线段 OA,OB,OC,OD 上取点 A',
B',C',D',使得 = = = = .
OA'
OA
OB'
OB
OC'
OC
OD'
OD
3.顺次连接点 A',B',C',D',所得四边形 就是所要求的图形.
如果在四边形外任选一点O,分别在OA,OB,OC,OD 的反向延长线上取点A‘, B’,C‘, D’,使得
= = = = 呢?如果点 O 取在四
边形 ABCD 内部呢?分别画出这时得到的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
作法二:
OA'
OA
OB'
OB
OC'
OC
OD'
OD
A'
B'
C'
D'
深化知识 实际应用
议一议 练一练
1.如图, △OAB和△OCD是位似图形,AB与CD平行吗 为什么
2.如图,以O为位似中心,将△ABC放大为原来的两倍.
议一议 练一练
3.如图,已知△ABC∽△DEF, 它们对应顶点的连线AD,BE,CF相交于点O,这两个三角形是不是位似三角形
0
B
E
C
F
A
D
议一议 练一练
平移、轴对称、旋转、位似
我们已经学过哪些图形变换?你能说出它们之间的异同吗?
在下列图案中,你能找出哪些变换
观察与发现
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.
A′(2,1),B′(2,0)
观察对应点之间的坐标的变化,你有什么发现
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为3:1,把线段AB缩小.
A′(2,1),B′(2,0)
A〞
B〞
A〞(-2,-1),B(-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
观察对应点之间的坐标的变化,你有什么发现
观察与发现
x
y
o
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2.
B
A
C
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
放大后对应点的坐标分别是多少
B'
A'
C'
观察与发现
x
y
o
在平面直角坐标系中, △ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2,将△ABC放大.
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
B
A
C
放大后对应点的坐标分别是多少
还有其他办法吗
观察与发现
典例应用 巩固新知
x
y
o
在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),
C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 )
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗 试试看.
巩固应用
x
y
o
B
1.如图表示△ABC把它缩小后得到的△COD,求它们的相似比
A
C
D
点D的横坐标为2
点B的横坐标为5
相似比为
x
y
2
4
6
8
2
4
6
8
-2
-4
-6
-8
-2
-4
-6
-8
O
9
10
11
12
-9
-10
-12
2. 如图,△ABC三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.
A
B
C
解:
A'( , ),B ' ( , ),C ' ( , ),
4
- 4
- 10
8
-4
10
A" ( , ),B" ( , ),C" ( , ),
4
- 4
- 8
10
-10
4
A'
B '
C '
A"
B"
C"
巩固应用
x
y
o
3.如图,写出矩形wxyz各点的坐标,如果矩形STUV相似于wxyz,点S 的坐标为(2,7),按照下列相似比,分别写出T、U、V各点的坐标.
W
x
y
z
(1)相似比为4;
(2)相似比为 ;
巩固应用
巩固应用
典例应用 巩固新知
如图,△ABO 的三个顶点的坐标分别为 A(-2,4),B(-2,0), O(0,0).以原点 O 为位似中心,画出一个三角形,使它与△ABO 的相似比为 .(注意单位长度)
y
x
O
4
4
-4
-4
B
A
归纳小结 自我反思
(1)本节课你学习了哪些知识?
(2)举例说明如何利用位似,将一个图形放大或缩小.
(3)以原点为位似中心的位似图形对应点的坐标有什么关系?用坐标表示位似图形的对应顶点时要注意什么?
(4)本节课运用了哪些数学思想方法研究问题?
布置作业
上本:教科书习题 27.3 第 2,3,4 ,5题.
谢 谢!
